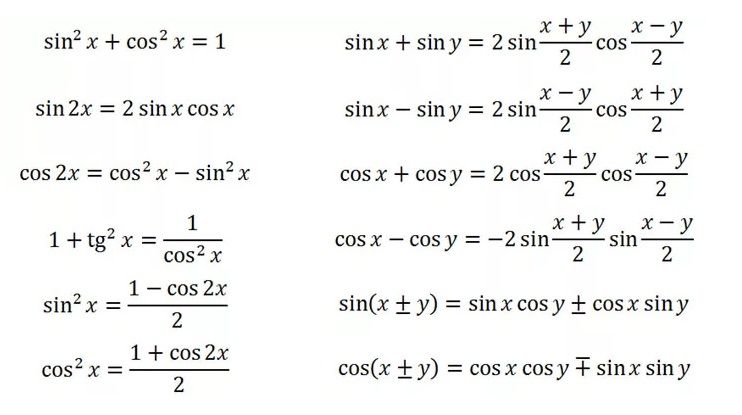Обзор инструментов группы Математические Тригонометрические (Trigonometric Math)—Справка
Доступно с лицензией Spatial Analyst.
Тригонометрические математические инструменты (группа Trigonometric Math) выполняют различные тригонометрические вычисления над значениями во входном растре.
Есть несколько общих категорий тригонометрических вычислений. Доступные инструменты в каждой категории перечислены здесь:
- Стандартные тригонометрические инструменты:
- Cos (косинус), Sin (синус), Tan (тангенс).
- Обратные (или «арк») тригонометрические инструменты:
- ACos (обратный косинус), ASin (обратный синус), ATan (обратный тангенс).
- Также есть обратный тангенс, основанный на x,y, как ATan2.
- Гиперболические тригонометрические инструменты:
- CosH (гиперболический косинус), SinH (гиперболический синус), TanH (гиперболический тангенс).
- Обратные гиперболические тригонометрические инструменты:
- ACosH (обратный гиперболический косинус), ASinH (обратный гиперболический синус), ATanH (обратный гиперболический тангенс).

- ACosH (обратный гиперболический косинус), ASinH (обратный гиперболический синус), ATanH (обратный гиперболический тангенс).
В следующей таблице перечислены доступные тригонометрические математические инструменты, и предоставлено краткое описание каждого:
| Инструмент | Описание |
|---|---|
Арккосинус (ACos) | Вычисляет арккосинус ячеек растра. |
Арккосинус (ACos) | Вычисляет гиперболический арккосинус ячеек растра. |
Арксинус (ASin) | Вычисляет арксинус ячеек растра. |
Гиперболический арксинус (ASinH) | Вычисляет гиперболический арксинус ячеек растра. |
Арктангенс (ATan) | Вычисляет арктангенс ячеек растра. |
Арктангенс (ATan2) | Вычисляет гиперболический арктангенс ячеек растра. |
Арктангенс (AtanH) | Вычисляет гиперболический арктангенс ячеек растра. |
Косинус (Cos) | Вычисляет косинус ячеек растра. |
Гиперболический косинус (CosH) | Вычисляет гиперболический косинус ячеек растра. |
Инструмент Sin | Вычисляет синус значений ячеек растра. |
Синус (SinH) | Вычисляет гиперболический синус значений ячеек растра. |
Тангенс (Tan) | Вычисляет тангенс значений ячеек растра. |
Тангенс (TanH) | Вычисляет гиперболический тангенс значений ячеек растра. |
Малоугловое приближение | Brilliant Math & Science Wiki
Содержание
- Выводы приближения
- Приложения в физике
Геометрически
Малоугловые аппроксимации могут быть получены геометрически без использования вычислений. Рассмотрим приведенную ниже диаграмму прямоугольного треугольника, одна сторона которого касается окружности: 94). \end{выровнено} sinθcosθ=n=0∑∞(2n+1)!(−1)nθ2n+1=θ−3!θ3+O(θ5)=n=0∑∞(2n)!(−1) nθ2n=1−2!θ2+O(θ4).
Малоугловые аппроксимации соответствуют младшим аппроксимациям этих рядов Тейлора, как видно из приведенных выше разложений. 2 x}.f(x) )=cot2xsecxtanx−csc2x. 95\big),f(x)≈−1−x2+x3−32x4+O(x5),
2 x}.f(x) )=cot2xsecxtanx−csc2x. 95\big),f(x)≈−1−x2+x3−32x4+O(x5),
, что согласуется с улучшенным приближением к первым трем порядкам.
Построив три аппроксимации, мы видим, что наивная аппроксимация работает довольно плохо, а улучшенная аппроксимация намного лучше. Улучшенное приближение для косинуса добавило член младшего порядка , который был пропущен в наивном приближении, иллюстрируя опасности, связанные с наивным приближением при делении на функции. Для наибольшей точности следует использовать ряд Тейлора самой функции f(x)f(x)f(x), а не ряды для синуса и косинуса по отдельности: 92}{2}2θ2
Какой поправочный член низшего порядка для малоугловой аппроксимации функции синуса
sinθ≈θ?\sin \theta\приблизительно \theta?sinθ≈θ?
Под каким углом в радианах с точностью до тысячных (\big((в диапазоне [0,2π))[0,2\pi)\big)[0,2π)) относительная ошибка между tanθ\ tan \thetatanθ и его малоугловое приближение низшего порядка превышают 5%?
Малоугловое приближение повсеместно используется во всех областях физики, включая механику, волны и оптику, электромагнетизм, астрономию и многое другое.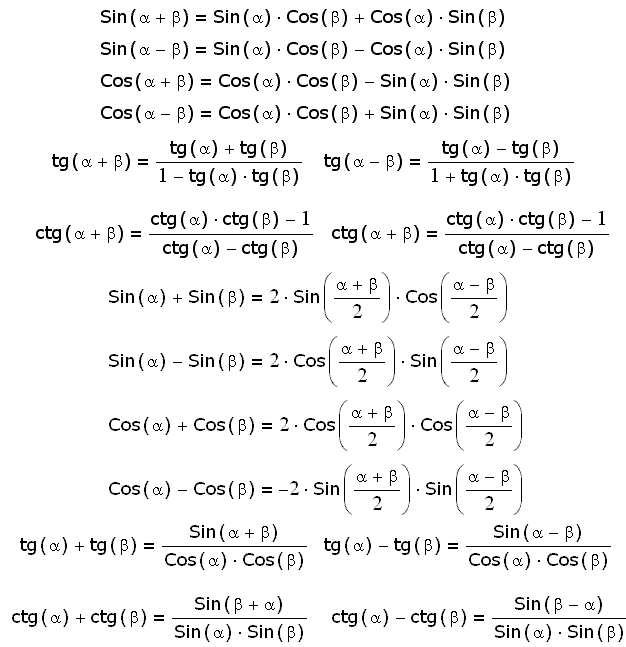 Ниже рассмотрено несколько хорошо известных примеров, чтобы проиллюстрировать, почему малоугловое приближение полезно в физике.
Ниже рассмотрено несколько хорошо известных примеров, чтобы проиллюстрировать, почему малоугловое приближение полезно в физике.
Простой маятник
Малые колебания простого маятника лучше всего моделировать в малоугловом приближении.
Небольшие колебания простого маятника являются основным примером в механике, где малоугловое приближение абсолютно необходимо для достижения любого полезного аналитического прогресса. Из вращательной формы второго закона Ньютона крутящий момент τ\tauτ на маятнике массой mmm от силы тяжести, когда он колеблется вокруг точки вращения на струне длиной ℓ\ellℓ, равен 92 \ddot{\theta} \ подразумевает \ddot{\theta} + \frac{g}{\ell} \sin \theta = 0,τ=Iα⟹−ℓmgsinθ=mℓ2θ¨⟹θ¨+ℓgsinθ=0 ,
, где θ\thetaθ — угол между струной и вертикалью.
Решения этого уравнения движения можно найти в терминах функций, называемых эллиптическими интегралами, с которыми трудно работать вручную.
θ¨+gℓsinθ=0 ⟹ θ¨+gℓθ=0.\ddot{\theta} + \frac{g}{\ell} \sin \theta = 0 \ подразумевает \ddot{\theta} + \frac{g}{\ell} \theta = 0,θ¨+ℓgsinθ=0⟹θ¨+ℓgθ=0.
Новое дифференциальное уравнение легко разрешимо. Решения выглядят как θ(t)=Acos(gℓt)+Bsin(gℓt)\theta(t) = A\cos\left(\sqrt{\frac{g}{\ell}} t\right)+ B\sin\left(\sqrt{\frac{g}{\ell}} t\right)θ(t)=Acos(ℓgt)+Bsin(ℓgt) для констант AAA и BBB в зависимости от начальные условия, успешно воспроизводящие колебательное поведение маятника.
Угловое расстояние в астрономии
Размер или расстояние между небесными телами в астрономии обычно записывается в терминах угловой диаметр или видимый размер , то есть угол θ\thetaθ между двумя телами, видимыми с Земли. Если расстояние между двумя удаленными точками равно ddd, а средняя точка между точками находится на расстоянии DDD от Земли, то этот угол подчиняется соотношению
tanθ2=d2D. \tan \frac{\theta}{2} = \frac {d}{2D}.tan2θ=2Dd.
\tan \frac{\theta}{2} = \frac {d}{2D}.tan2θ=2Dd.
Диаграмма, соответствующая этой формуле, приведена ниже:
Угловое расстояние между двумя далекими звездами, как видно с Земли
Используя малоугловое приближение, угловое расстояние можно переписать как
θ=dD.\theta = \frac{d}{D}.θ=Dd.
Приближение полезно, поскольку обычно угловое расстояние проще всего измерить в астрономии, а разница между углами настолько мала, что сам угол более полезен, чем синус.
В одном градусе 60 угловых минут, а угловой диаметр Солнца составляет примерно 323232 угловых минуты. Зная, что Солнце находится на расстоянии около 888 световых минут от Земли, оцените диаметр Солнца. 98 \text{ м}3,7×108 м от Земли. Что из следующего является наилучшей аппроксимацией диаметра Луны в метрах?
Однощелевая дифракция
При однощелевой дифракции свет, проходящий через барьер с щелью, превышающей одну длину волны света, имеет профиль интенсивности, измеренный за барьером, который демонстрирует характерную картину пиков и впадин.
Условие минимума в этом распределении интенсивности:
dsinθ=mλ,d \sin \theta = m \lambda,dsinθ=mλ,
где ddd — ширина щели, θ\thetaθ — угол от центра щели до точки измерения, λ\lambdaλ — длина волны света, а mmm — целое число, отличное от нуля.
Это условие можно переписать в терминах расстояния по вертикали от центра экрана измерений, yyy, как показано на диаграмме выше. Предположим, что экран измерения представляет собой расстояние DDD от барьера. Обычно считается, что DDD намного больше, чем ddd, и можно использовать малоугловое приближение для θ\thetaθ. Тогда формула для минимумов интенсивности принимает вид
y=mλDd,y = \frac{m \lambda D}{d},y=dmλD,
удобное выражение для длины волны света, ширины щели и расстояния от барьера до экран.
λad\frac{\lambda a}{d}dλa 2λda\frac{2\lambda d}{a}a2λd 2λad\frac{2\lambda a}{d}d2λa λda\frac{\lambda d}{a}aλd
В однощелевом дифракционном эксперименте с шириной щели aaa, расстоянием ddd между барьером и измерительным экраном и светом с длиной волны максимальный пик?
Процитировать как: Малоугловое приближение.
Brilliant.org . Полученное из https://brilliant.org/wiki/small-angle-closed/
Син Тан Кос?
- 09.12.2021
- 93
Индис
- Син Тан Кос?
- Использовать Костан или грех?
- Как загар соотносится с грехом и косой?
- Как получить загар от COS и греха?
- Что такое формула cos?
- Чему равен cos sin?
- Как вы находите грех, данный Cos?
- Какова формула cos 3x?
- Какова формула греха Кос?
- Где равен Cos?
- Какая связь между sin, cos и Tan?
- Что означают sin, cos и Tan в исчислении?
- Что измеряют cos, sin и Tan?
Син Тан Кос?
Тангенс x определяется как его синус, деленный на его косинус: tan x = sin x cos x . Котангенс x определяется как косинус x, деленный на синус x: cot x = cos x sin x .
Использовать Костан или грех?
Sohcahtoa
Soh. ..
Синус = Противоположный / Гипотенуза …cah… Косинус = Смежный …toa Касательная = Противоположная / Смежная Как тан соотносится с sin и cos?
Косинус (часто сокращенно «cos») представляет собой отношение длины стороны, примыкающей к углу, к длине гипотенузы. А тангенс (часто сокращенно «тан») — это отношение длины стороны, противоположной углу, к длине прилежащей стороны. … SOH → sin = «противоположный» / «гипотенуза»
Как получить загар от COS и греха?
0:282:48Тригонометрия. Найдите точное значение sin cos и tan. Я бы взял соседнюю сторону и положил ее на гипотенузу. И если я хочуMoreIf я хочу сделать косинус.
Я бы взял соседнюю сторону и положил ее на гипотенузу. И если я хочу сделать тангенс. Я принимаю обратное. И положить его на соседнюю сторону.
Что такое формула cos?
Тогда формула косинуса: cos x = (прилежащая сторона) / (гипотенуза) , где «прилежащая сторона» — это сторона, примыкающая к углу x, а «гипотенуза» — самая длинная сторона (сторона, противоположная прямому углу) треугольника. …
Чему равен cos sin?
SINE, COSINEST и TAGNET
Функция SINE: SIN (θ) = противоположная / гипотенуза Функция косицинера: Cose (θsecent / vdracent / vdrasent / vdrasent / vdrasent / vdeneen / vdeneen / vdeneen / vdeneen / vden θ vden θ vden θ vden θ vducent / vden obine. 0243
Тангенс Функция: тангенс(θ) = Противоположный / Смежный Как найти sin при заданном Cos?
Все треугольники имеют 3 угла, сумма которых составляет 180 градусов. Следовательно, если один угол равен 90 градусам, мы можем вычислить Sin Theta = Cos (90 — Theta) и Cos Theta = Sin (90 — Theta).
Какова формула cos 3x?
Ответ: Выражение для cos 3x через cos x равно 4 cos3x — 3 cos x.
Какова формула греха Cos?
Синус угла (sin A) = длина противоположной стороны / длина гипотенузы. Косинус угла (cos A) = длина прилежащей стороны / длина гипотенузы. Тангенс угла (tan A) = длина противоположной стороны/длина соседней стороны.
Где равен Cos?
Всегда, всегда синус угла равен противолежащему катету, деленному на гипотенузу (opp/hyp на диаграмме).




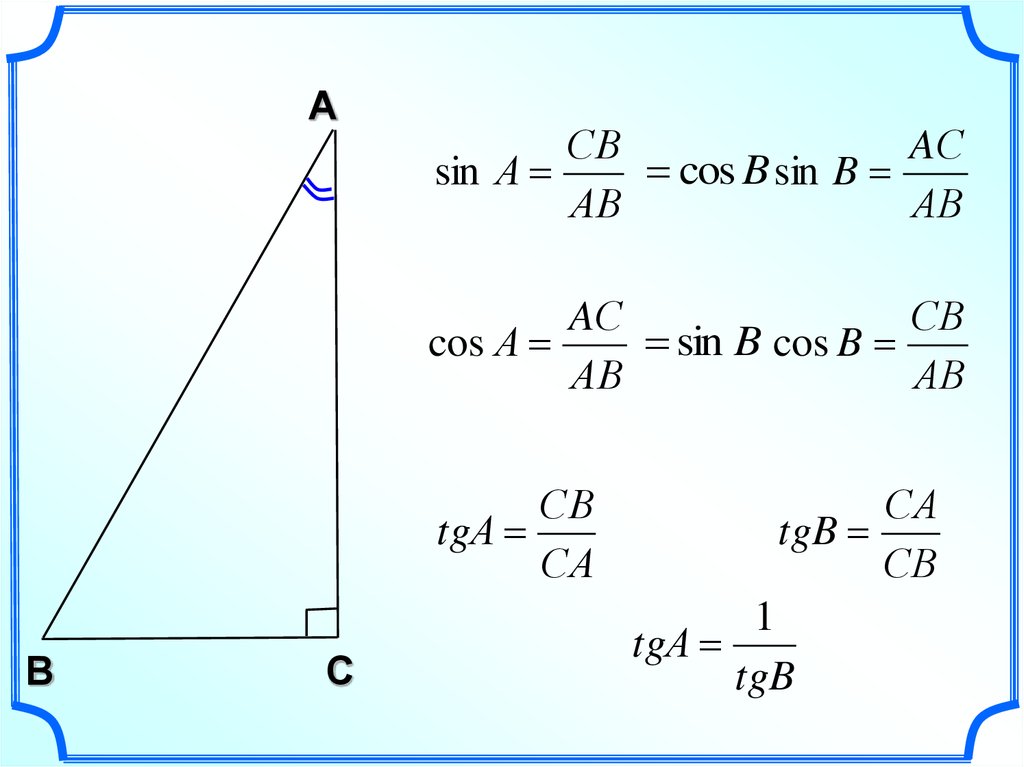 Условие минимума в этом распределении интенсивности:
Условие минимума в этом распределении интенсивности: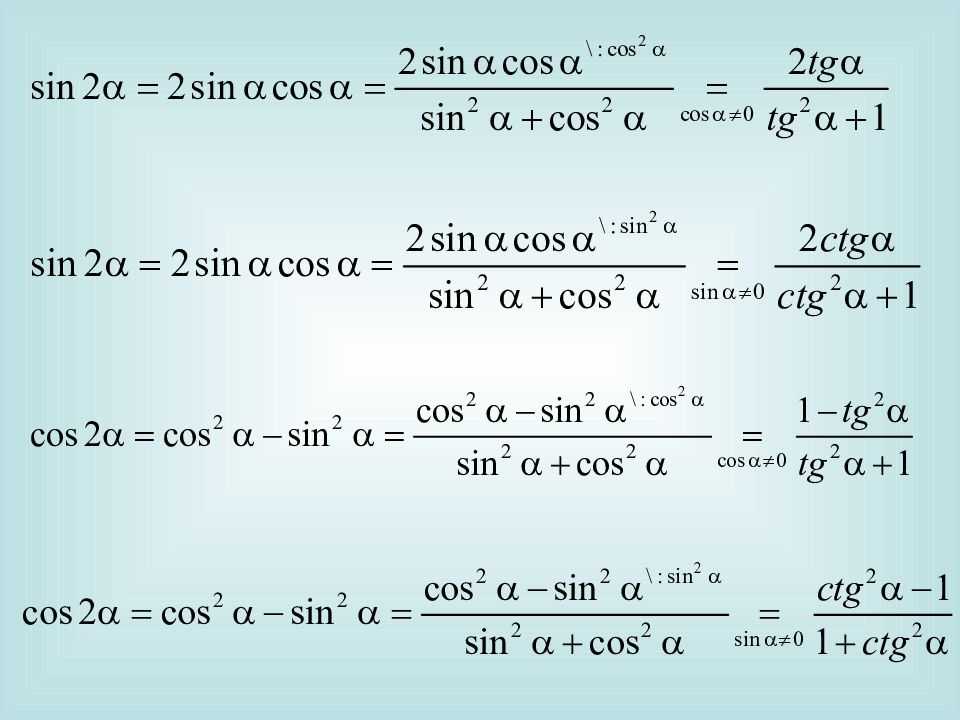 Brilliant.org .
Полученное из
https://brilliant.org/wiki/small-angle-closed/
Brilliant.org .
Полученное из
https://brilliant.org/wiki/small-angle-closed/ ..
.. Я бы взял соседнюю сторону и положил ее на гипотенузу. И если я хочу сделать тангенс. Я принимаю обратное. И положить его на соседнюю сторону.
Я бы взял соседнюю сторону и положил ее на гипотенузу. И если я хочу сделать тангенс. Я принимаю обратное. И положить его на соседнюю сторону. 0243
0243