Cos2X как разложить: Подскажите ,cos2x чему равен? — ответ на Uchi.ru

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )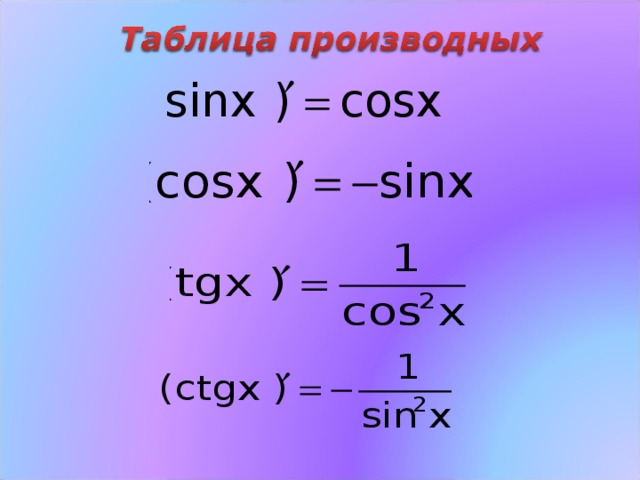
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74 Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81
Найти точное значение		sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Все формулы по тригонометрии

Все формулы по тригонометрии

Подождите пару секунд пока подгрузятся формулы

Основные тригонометрические тождества

$$sin^2x+cos^2x=1$$

$$tgx= \frac{sinx}{cosx}$$

$$ctgx= \frac{cosx}{sinx}$$

$$tgxctgx=1$$

$$tg^2x+1= \frac{1}{cos^2x}$$

$$ctg^2x+1= \frac{1}{sin^2x}$$

Формулы двойного аргумента (угла)

$$sin2x=2cosxsinx$$

\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}

\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}

\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}

\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}

\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}

Формулы тройного аргумента (угла)

$$sin3x=3sinx-4sin^3x$$

$$cos3x=4cos^3x-3cosx$$

$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$

$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$

Формулы половинного аргумента (угла)

$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$

$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$

$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$

$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$

\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}

\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}

Формулы квадратов тригонометрических функций

$$sin^2x= \frac{1-cos2x}{2}$$

$$cos^2x= \frac{1+cos2x}{2}$$

$$tg^2x= \frac{1-cos2x}{1+cos2x}$$

$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$

$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$

$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$

$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$

$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$

Формулы кубов тригонометрических функций

$$sin^3x= \frac{3sinx-sin3x}{4}$$

$$cos^3x= \frac{3cosx+cos3x}{4}$$

$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$

$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$

Формулы тригонометрических функций в четвертой степени

$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$

$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$

Формулы сложения аргументов

$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$

$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$

$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$

$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$

$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$

$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$

$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$

$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$

Формулы суммы тригонометрических функций

$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$

Формулы разности тригонометрических функций

$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$

$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$

$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$

$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$

$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$

Формулы произведения тригонометрических функций

$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$

$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$

$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$

\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}

\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}

$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$

© 2012–2021 100formul. ru
САЙТ ПРОДАЕТСЯ !!! Написать нам: [email protected]


2}$ с использованием ряда Маклорена для $\cos2x$

Задай вопрос

спросил

Изменено 3 года, 9 месяцев назад

Просмотрено 809 раз

$\begingroup$

94}{6!} …$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

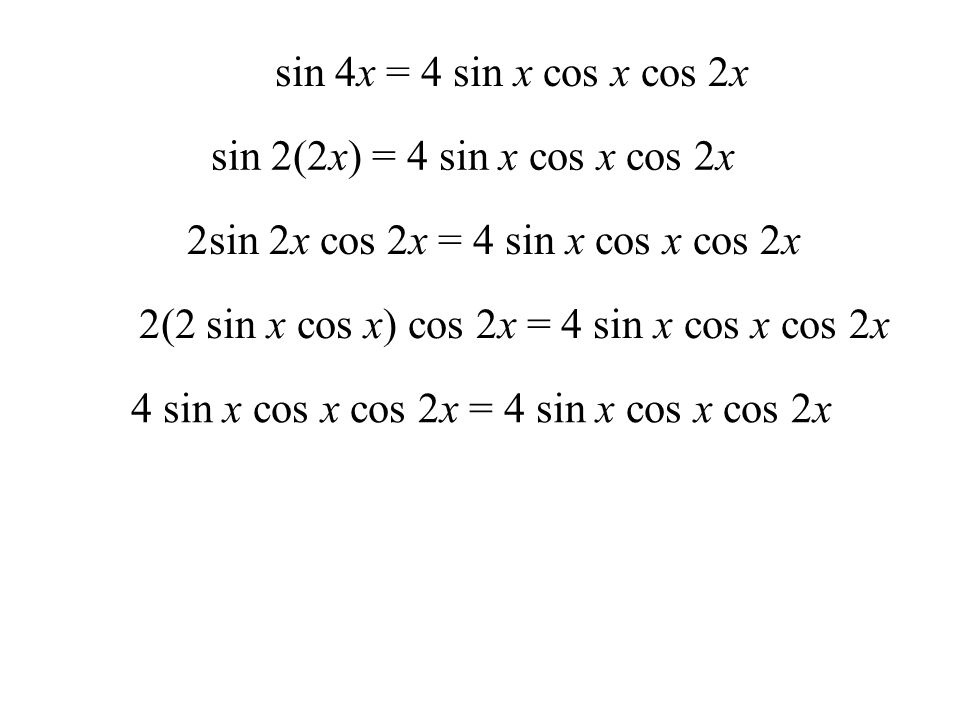. 92-6x+8)

Онлайн-калькулятор доменов и диапазонов — Wolfram|Alpha

www.wolframalpha.com › калькуляторы › домен-ран…

Wolfram|Alpha — отличный инструмент для определения доменов и диапазонов функции. Он также показывает графики функции и иллюстрирует домен и диапазон на …

Калькулятор поиска домена — Mathway

www.mathway.com › Калькулятор › поиск домена

Калькулятор домена позволяет найти область определения функций и выражений и получить результаты в интервальной и заданной нотации.

Bilder

Alle anzeigen

Alle anzeigen

Свойства функции: Домен — YouTube

www.youtube.com › смотреть

18.12.2016 найти домен … проверить …
Дауер: 4:05
Прислан: 18.12.2016

Symbolab Math Solver & Homework Helper поможет вам шаг за шагом, как … Бесплатные функции калькулятор домена — найти функции домена шаг за шагомFind . ..

Как найти домен и диапазон функции с помощью этих онлайн …

www.makeuseof.com › Интернет

24.07.2021 · Symbolab также предлагает хороший онлайн-калькулятор, помогающий в различных вычислениях. Введите функцию в строку поиска и результаты …

Symbolab Composition Of Functions

awwe.etcasaimmobiliare.it › symbolab-composition-…

Калькулятор домена и диапазона бесплатных функций — поиск домена и диапазона функций шаг за шагом. Для выполнения композиции функций нужно всего лишь выполнить …

кусочно-функциональное обозначениеb

mahaguru.de › кусочно-функционально-символическое обозначение

Измените область определения на заданный интервал уравнения. Если односторонние пределы одинаковы, то предел существует. Определите константу нормализации для …

Ähnliche Fragen

Как найти область определения функции?

Как найти домен графа?

Что такое домен и диапазон в интервальной записи?

Калькулятор составных функций — eMathHelp

www.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *