Производные, определение производных, дифференциалов, правила для дифференциалов
Определение производной
Если y = f(x), производная функции y или f(x) по отношению к x определяется как
13.1
где h = Δx. Производная также обозначается как y’, df/dx от f'(x). Процесс взятия производной называется дифференцированием.
В нижеследующем u, v, w есть функции x; a, b, c, n — константы [ограниченные, если указано]; e = 2.71828… есть натуральная основа логарифмов; ln u — натуральный логарифм u [т.е. логарифм по основанию е] где предполагается, что u > 0 и все углы — в радианах.
Производные тригонометрических и обратных тригонометрических функцийПроизводные экспоненциальных и логарифмических функцийПроизводные гиперболических и обратных гиперболических функцийВторая, третья и более высокие производные определяется следующим образом.
13.43 Вторая производная = (d/dx).(dy/dx) = d2y/dx2 = f»(x) = y »
13.44 Третья производная = (d/dx).(d2y/dx2) = d3/dx3 = f»'(x) = y»’
13.45 n-ая производная = (d/dx).(dn — 1
Пусть Dp с оператором dp/dxp так, что DP u = dpu/dxp = p-ый дериватив u. Тогда
13.46
где есть биномиальные коэффициенты.
Как особый случай, мы имеем
13.47
13.48
Пусть y = f(x) и Δy = f(x + Δx) — f(x). Тогда
13.49 Δy/Δx = [f(x + Δx) — f(x)]/Δx = f'(x) + ε = dy/dx + ε
где ε → 0 когда Δx → 0. Таким образом,
13.50 Δy = f'(x)Δx + εΔx
Если мы назовем Δx = dx дифференциалом x, тогда мы определяем дифференциал y как
13.
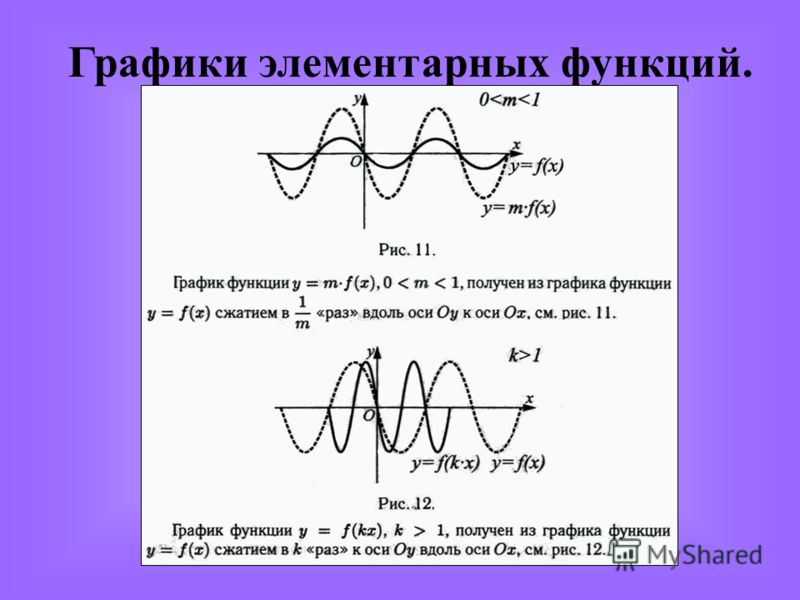51 dy = f'(x)dx
Правила для дифференциалов
Правила для дифференциалов аналогичны правилам для производных. В качестве примера отметим, что
Частные производные
Пусть f(x, y) будет функцией двух переменных x и y. Тогда мы определяем частную производную f(x, y) по x, сохраняя у постоянным, как
Подобно, частная производная f(x, y) по y, сохраняя x постоянным, будет
13.59
Частные производные высших порядков могут быть определены следующим образом.
13.60
13.61
Результаты в 13.61 будут равны, если функция и ее частные производные являются непрерывными, т.е. в этом случае порядок дифференцирования не имеет значения.
Дифференциал f(x, y) определяется как
13.62
где dx = Δx и dy = Δy.
Применение к функциям, имеющим более чем две переменные, в точности аналогично.
Производная как смысл жизни или что такое дифференциал(d) / Хабр
Пролог:
Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.
Начало
Для начала лучше ознакомиться со статьей о самой прозводной(скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.
Как мы уже знаем формула записи производной выглядит так:
-напоминаю, что Δx — приращение аргумента, Δy — приращение функции.
Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность».
Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано).
Теперь выразим из этого равенства приращение функции(Δy):
И на этом следует пока остановиться и рассмотреть график.
Смотрим дифференциалу в лицо
Расмотрим такой график:
Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.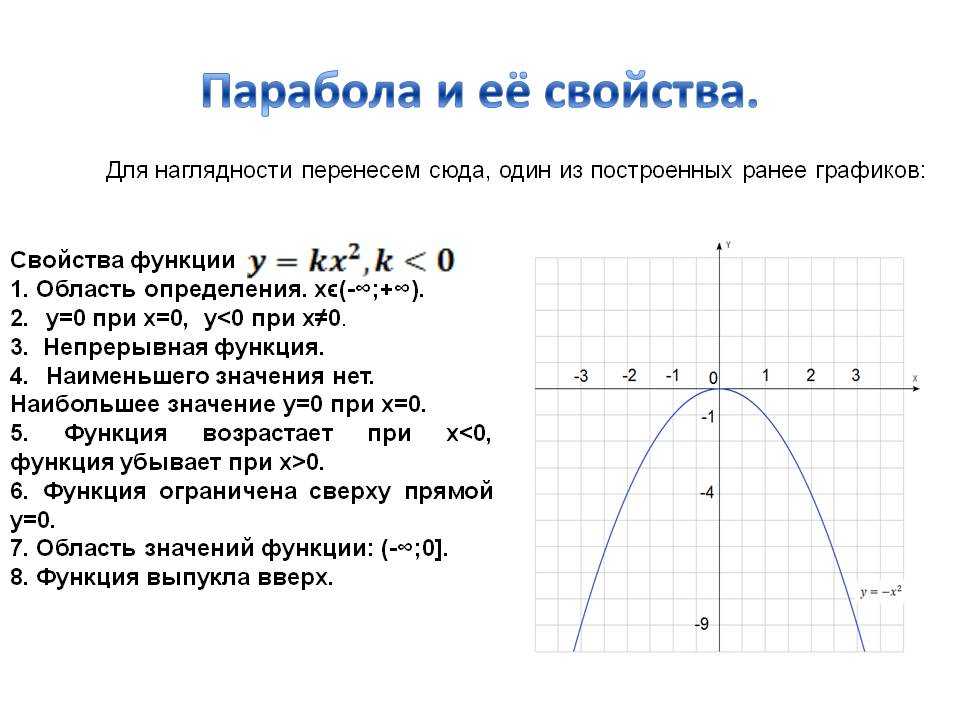
Как мы видим приращение функции(Δy) как бы разделено на две части: BC и CD.
И ведь по-сути нам ведь интересна именно та часть, которая показывает на сколько изменился у относительно касательной — то есть BC, а CD — это лишь та «погрешность» которая нам не особо интересна, поэтому введем понятие дифференциала:
Дифференциал(d) — это линейная часть приращения функции.
Дифференциал функции(dy) — это главная линейная часть приращения функции.
Зная это введем обозначение на графике:
Вернемся к равенству
BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.
Из формулы мы понимаем, что dy=f'(x)Δx.
Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).
Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.
Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx
И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.
Немного пределов
Добавим с левой части и с правой предел
Тогда:
В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:
Зная, что f'(x)Δx = dy, мы делаем вывод, что:
Тогда так же мы можем сказать, что дифференциал функции — это приращения функции у которой приращение аргумента стремиться к нулю, ну и это следуется из того же графика.
В свою очередь dx по прежнему Δx
Производные как dy/dx
Производные все о изменение …
… они показывают, как быстро что-то меняется (так называемая скорость изменения ) в любой момент.
В разделе «Введение в производные» (пожалуйста, прочтите сначала!) мы рассмотрели, как построить производную, используя разности
Здесь мы делаем то же самое, но с использованием нотации «dy/dx» (также называемой обозначение Лейбница ) вместо пределов.
Начнем с вызова функции «y»:
у = f(x)
1. Добавьте Δx
Когда x увеличивается на Δx, тогда y увеличивается на Δy :
у + Δу = f(х + Δх)
2. Вычесть две формулы
| От кого: | у + Δу = f(х + Δх) | |
| Вычесть: | у = f(x) | |
| Получить: | y + Δy − y = f(x + Δx) − f(x) | |
| Упрощение: | Δy = f(x + Δx) − f(x) |
3. Скорость изменения
Чтобы определить, насколько быстро (называется скорость изменения
) мы делим на Δx :Δy Δx = f(x + Δx) − f(x) Δx
4. Уменьшить Δx близко к 0
Мы не можем допустить, чтобы Δx стало равным 0 (потому что это было бы делением на 0), но мы можем заставить его направиться к нулю и назвать его «dx»:
Δx dx
Вы также можете думать о «dx» как о бесконечно малом или бесконечно малом.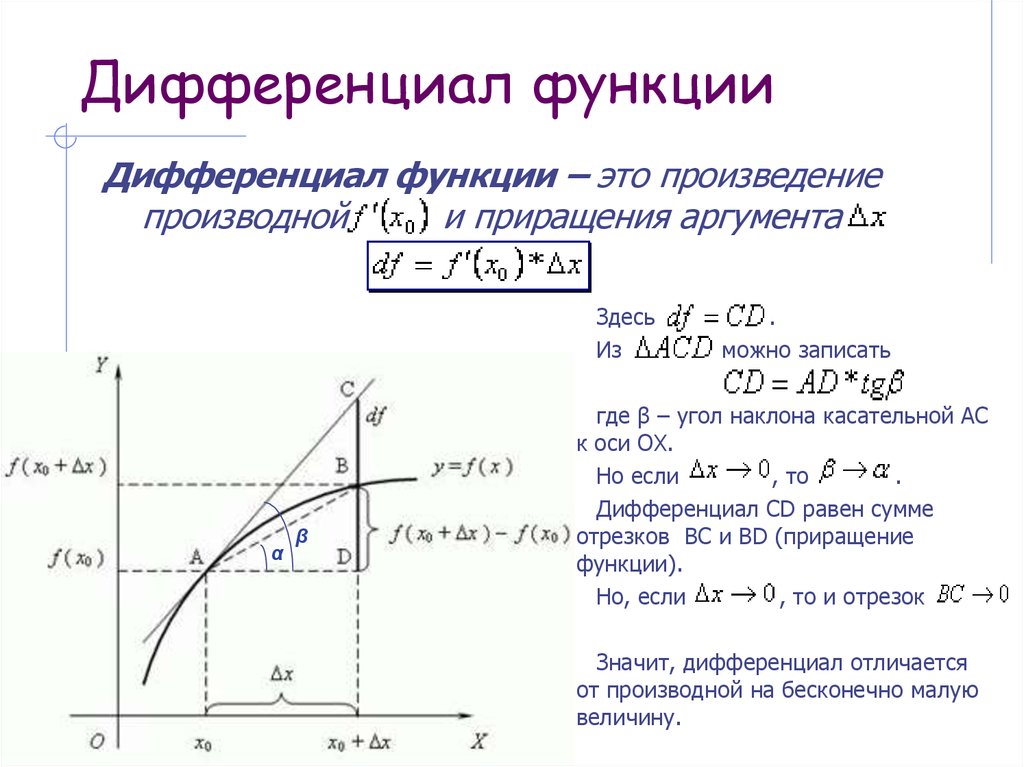
Точно так же Δy становится очень маленьким, и мы называем его «dy», чтобы получить:
д дх знак равно е (х + дх) — е (х) дх
Попробуйте функцию
Попробуем f(x) = x 2
| д дх | = е (х + дх) — е (х) дх | ||
| = (х + дх) 2 − х 2 дх | f(x) = x 2 | ||
| = x 2 + 2x(dx) + (dx) 2 − x 2 дх | Расширить (x+dx) 2 | ||
| = 2x(дх) + (дх) 2 дх | x 2 −x 2 =0 | ||
| = 2х + дх | Упростить дробь | ||
| = 2x | dx идет к 0 |
Таким образом, производная от x 2 равна 2x
.
Почему бы вам не попробовать это на f(x) = x
3 ?| д дх | = е (х + дх) — е (х) дх | ||
| = (х + дх) 3 − х 3 дх | f(x) = x 3 | ||
| = x 3 + … (ваша очередь!) дх | Расширить (x+dx) 3 |
Какое производное вы получаете?
Новые кадры подтверждают, что фальшивый избиратель Трампа провел несколько часов в избирательном штабе Джорджии в день взлома
Вашингтон Си-Эн-Эн —
Недавно полученное видео наблюдения впервые показывает, что произошло в избирательном участке округа Джорджия в тот день, когда стало известно, что его системы голосования были взломаны 7 января 2021 года.
Чиновник республиканского округа в Джорджии и оперативники, работающие с адвокатом бывшего президента Дональда Трампа, в тот день провели несколько часов в закрытой зоне избирательного участка округа Кофе. Среди тех, кто был замечен на кадрах, Кэти Лэтэм, бывший председатель Республиканской партии округа Кофе, в отношении которой ведется уголовное расследование за то, что она выдавала себя за фальшивого избирателя в 2020 году.
CNN ранее сообщал, что 7 января 2021 года Лэтэм сопровождала оперативников, работающих с бывшим адвокатом Трампа Сидни Пауэллом, через парадную дверь избирательной комиссии. Новые кадры, похоже, опровергают предыдущие заявления Лэтэм о том, что она не была «лично причастна» к взлому.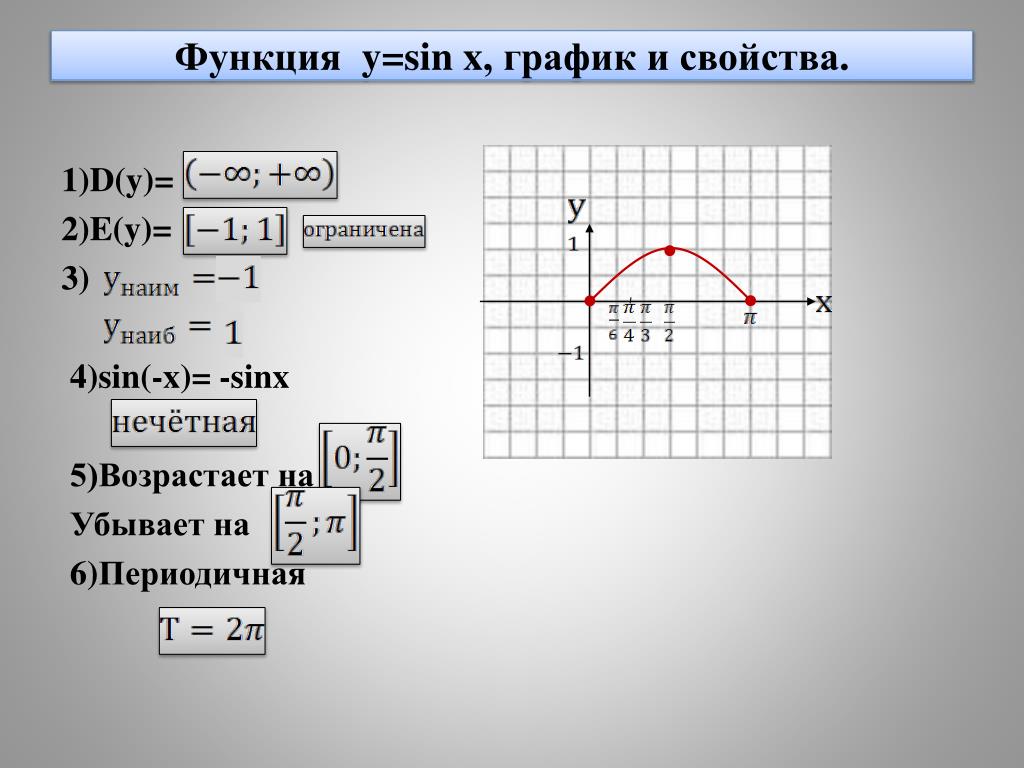
Смотрите видео, как бывший чиновник из Грузии сопровождает оперативников Трампа в избирательные участки
02:20 — Источник: CNN
Новое видео, полученное в рамках многолетнего гражданского судебного процесса в Джорджии, связанного с безопасностью систем голосования, показывает, что Лэтэм оставался в офисе в течение нескольких часов, пока те же самые оперативники устанавливали компьютеры рядом с избирательным оборудованием и, по-видимому, получали доступ к данным голосования.
Маджио не ответил на запрос CNN о комментариях. Информационная фирма SullivanStrickler, на которую он работает, которая, как показывают судебные документы, была нанята Пауэллом, ранее заявила в заявлении для CNN, что «адвокаты поручили связаться с окружными избирательными властями для получения доступа к определенным данным» в Джорджии, а также «указали адвокатами для распространения этих данных среди определенных лиц».
В электронном письме от 29 августа 2022 года поверенный Салливана Стриклера признает, что Лэтэм был «основным контактным лицом» при координации визита команды в округ Кофе.
cms.cnn.com/_components/paragraph/instances/paragraph_143BDD93-BE0E-D588-AB69-5861D1C96F9C@published» data-editable=»text» data-component-name=»paragraph»>
Фирма заявила, что у нее нет оснований полагать, что эти адвокаты будут просить или указывать ей «сделать что-либо ненадлежащее или незаконное».Видео наблюдения показывает, как Кэти Лэтэм со Скоттом Холлом входят в избирательный офис округа Кофе 7 января 2021 года вместе с третьим неизвестным лицом.
Округ Кофе, Джорджия Недавно полученное видео наблюдения показывает, что фальшивый избиратель Трампа сопровождал оперативников в избирательную комиссию округа Джорджия, прежде чем взломать машину для голосования.
«Нет никаких известных нам свидетельств того, что миссис Лэтэм разговаривала с мисс Пауэлл или с кем-либо в SullivanStrickler 6 января 2021 года или ранее. И действительно, нам не известно никаких свидетельств того, что миссис Лэтэм разговаривала с мисс , Пауэллу или кому-либо в SullivanStrickler не позднее 6 января 2021 года», — добавил адвокат.
Второй адвокат, представляющий Лэтэма, Боб Чили, ранее сказал CNN: «Кэти Лэтэм на протяжении многих лет посвятила много времени и усилий защите честности выборов в округе Кофе, штат Джорджия. Она не будет и не была сознательно причастна к каким-либо нарушениям на каких-либо выборах».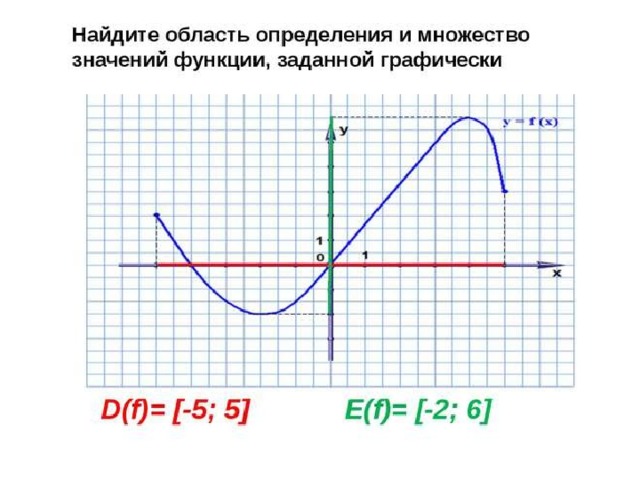
Холл, поручитель под залог в Атланте и наблюдатель за опросами республиканцев в округе Фултон, не ответил на неоднократные запросы CNN о комментариях.
На новом видео также видно, как третий оперативник, Джеффри Ленберг, входит в серверную комнату с ограниченным доступом в избирательном штабе округа Кофе более чем через две недели, 26 января. Ленберг находится под следствием генерального прокурора штата Мичиган в связи с серией голосований. системные бреши там.
Также в конце января 2021 года доступ к избирательному офису округа Кофе получил генеральный директор Cyber Ninjas Дуг Логан, который руководил партийным аудитом выборов в округе Марикопа, штат Аризона, а также является объектом уголовного расследования в Мичигане.
Согласно судебным документам, Логан и Маджио являются частью команды, которая получила доступ к системам голосования в округе Антрим, штат Мичиган, в конце 2020 года, что в конечном итоге привело к опровергнутому отчету об уязвимостях системы голосования Доминиона, который остается в центре необоснованных заявления о широкомасштабном мошенничестве на выборах, выдвинутые Трампом и его союзниками.
Видео наблюдения снаружи здания показывает, что Логан несколько раз посещал избирательный участок округа Кофе в январе 2021 года, примерно через две недели после того, как произошло нарушение. CNN связался с адвокатами Логана.