Практическое занятие 3+СР(координаты вектора)
Практическое занятие № 3
(Координаты вектора)
Найдите координаты точки M, делящей отрезок, ограниченный точками M1(2; 3) и M2(–5; 1), в отношении: 1) , 2) , 3) , 4) .
Ответ: 1) , 2), 3) , 4) .
Пусть в данной аффинной системе координат даны точки Точки C, D, E делят отрезок AB на четыре равные части. Найти координаты этих точек.
Ответ: , , 3) .
Найти длины векторов, заданных своими координатами в ПДСК: , , , , .
Ответ: .
Даны векторы , , .

; 2); 3); 4).
Ответ: 1) , 2), 3), 4).
Найти координаты вектора , направляющие косинусы которого равны , если он образует с ортом острый угол и имеет длину . Ответ:
Три некомпланарных вектора попарно ортогональны, а их длины соответственно равны 2, 3, 6. Найти длину вектора и направляющие косинусы этого вектора в ПДСК, связанной с векторами .
Ответ:
Дан куб ABCDA1B1C1D1 со стороной AB = 7. Точка T делит ребро DD1 в отношении 2:5, а точка S
делит ребро B1C1 в отношении 3:4. Найти длину отрезка TS.
Найти длину отрезка TS.
Ответ:
В прямоугольном параллелепипеде со сторонами , , точка M делит отрезок AC1 в отношении 2:1, точка N ребро BB1 – в отношении 5:1, точка Q делит отрезок D1C в отношении 2:1. Найти:
расстояние между точками N и Q;
расстояние от точки M до плоскости ВВ1С1С.
Ответ:
Самостоятельная работа
Даны три вектора . Найти векторы и . (1184)
Ответ:
Даны три вектора . Подобрать числа и так, чтобы три вектора , и составили треугольник, если начало вектора совместить с концом вектора , а начало вектора с концом вектора .
 (1185)
(1185)
Ответ:
Из одной точки проведены векторы . Найти координаты единичного вектора, который, будучи проведен из той же точки, делил бы угол между и пополам. (1188)
Ответ:
Даны три вектора . Найти векторы и . (1190)
Ответ:
Относительно ортонормированного базиса дан вектор . Найти единичный вектор, имеющий то же направление, что и вектор . (1195)
Ответ:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному. Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Если даны две точки плоскости и , то вектор имеет следующие координаты: Если даны две точки пространства и , то вектор имеет следующие координаты: То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Задание: Для тех же точек запишите формулы нахождения координат вектора . Формулы в конце урока. Пример 1 Даны две точки плоскости и . Найти координаты вектора Решение: по соответствующей формуле: Как вариант, можно было использовать следующую запись: Эстеты решат и так: Лично я привык к первой версии записи. Ответ: По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь: Обязательно нужно понимать различие между координатами точек и координатами векторов: Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя. Координаты же вектора – это его разложение по базису , в данном случае . Записи координат точек и координат векторов вроде бы схожи: , асмысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства. Дамы и господа, набиваем руку: Пример 2 а) Даны точки и . Найти векторы и . Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока. Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Как найти длину отрезка? Длина, как уже отмечалось, обозначается знаком модуля. Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле Если даны две точки пространства и , то длину отрезка можно вычислить по формуле Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант Пример 3 Даны точки и . Найти длину отрезка . Решение: по соответствующей формуле: Ответ: Для наглядности выполню чертёж Отрезок – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка. Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить: Во-первых, в ответе ставим размерность: «единицы». Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи: Читаем!!! Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя. Вот другие распространенные случаи: Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д. В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя. Давайте заодно повторим возведение корней в квадрат и другие степени: Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно. Задание для самостоятельного решения с отрезком в пространстве: Пример 4 Даны точки и . Найти длину отрезка . Решение и ответ в конце урока. Как найти длину вектора? Если дан вектор плоскости , то его длина вычисляется по формуле . Если дан вектор пространства , то его длина вычисляется по формуле . Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора. Пример 5 Даны точки и . Найти длину вектора . Я взял те же точки, что и в Примере 3. Решение: Сначала найдём вектор : По формуле вычислим длину вектора: Ответ: Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3 знаков после запятой. Выполним чертеж к задаче: В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка равна длине вектора . Так же очевидно, что длина вектора будет такой же. По итогу: Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки и . Найти длину отрезка . Вместо применения формулы , поступаем так: Этот способ широко практикуется в ходе решений задач аналитической геометрии. Вышесказанное справедливо и для пространственного случая Для тренировки: Пример 6 а) Даны точки и . Найти длину вектора . Решения и ответы в конце урока.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
2.2: Векторные уравнения и промежутки
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 70187
- Дэн Маргалит и Джозеф Рабинофф
- Технологический институт Джорджии
Цели
- Понять эквивалентность между системой линейных уравнений и векторным уравнением.
 3\).
3\). - Словарное слово: векторное уравнение .
- Основное словарное слово: диапазон .
Векторные уравнения
Уравнение, включающее векторы с \(n\) координатами, аналогично \(n\) уравнениям, включающим только числа. Например, уравнение
\[x\left(\begin{array}{c}1\\2\\6\end{array}\right) +y\left(\begin{array}{c}- 1\\-2\\-1\end{массив}\right)=\left(\begin{массив}{c}8\\16\\3\end{массив}\right)\nonnumber\]
упрощается до
\[\left(\begin{array}{c}x\\2x\\6x\end{array}\right)+\left(\begin{array}{c}-y\\ -2y\\-y\end{массив}\right)=\left(\begin{массив}{c}8\\16\\3\end{массив}\right)\quad\text{or}\quad \left(\begin{массив}{c}xy\\2x-2y\\6x-y\end{массив}\right)=\left(\begin{массив}{c}8\\16\\3\ end{array}\right).\nonumber\]
Чтобы два вектора были равны, все их координаты должны быть равны, так что это просто система линейных уравнений
\[\left\{\begin{array }{rrrrc}x &-& y &=& 8\\ 2x &-& 2y &=& 16\\ 6x &-& y &=& 3. \end{массив}\right.\nonumber\]
\end{массив}\right.\nonumber\]
Определение \(\PageIndex{1}\): Векторное уравнение
Векторное уравнение представляет собой уравнение, включающее линейную комбинацию векторов с возможными неизвестными коэффициентами.
Примечание \(\PageIndex{1}\)
Вопрос о том, имеет ли векторное уравнение решение, аналогичен вопросу о том, является ли данный вектор линейной комбинацией некоторых других заданных векторов.
Например, приведенное выше векторное уравнение спрашивает, является ли вектор \((8,16,3)\) линейной комбинацией векторов \((1,2,6)\) и \((-1,2 ,-1)\).
На самом деле нас волнует решение систем линейных уравнений, а не решение векторных уравнений. Весь смысл векторных уравнений в том, что они дают нам другой, более геометрический способ рассмотрения систем линейных уравнений.
Примечание \(\PageIndex{2}\): Изображение согласованной системы
Ниже мы покажем, что приведенная выше система уравнений непротиворечива.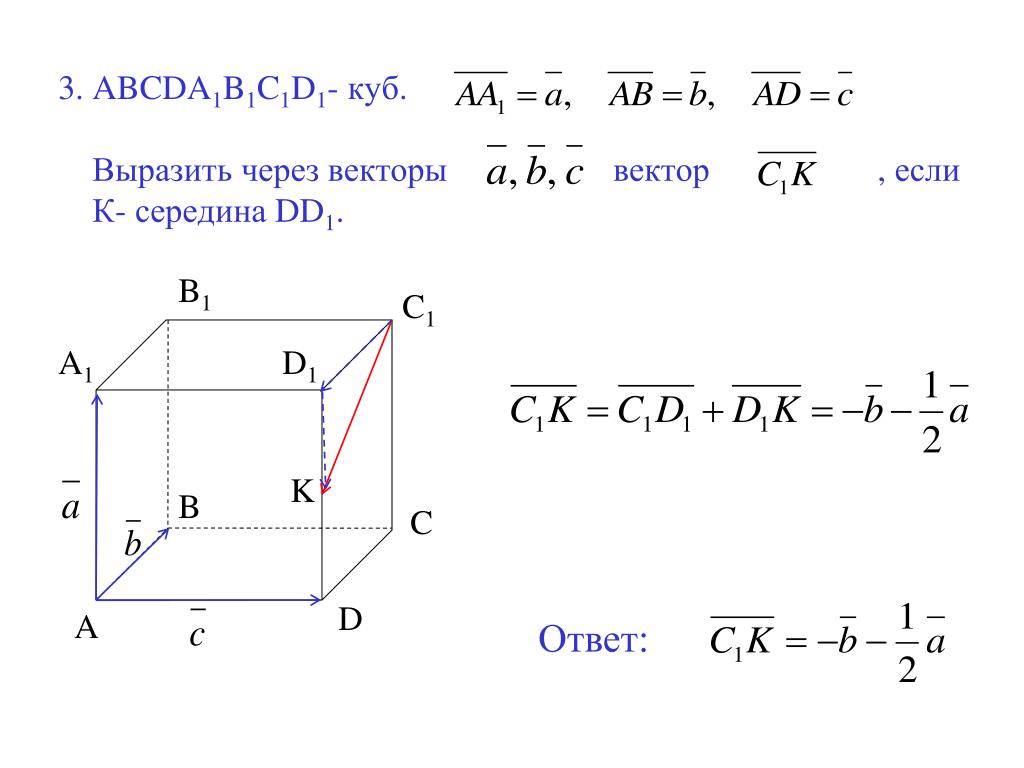 Эквивалентно, это означает, что приведенное выше векторное уравнение имеет решение. Другими словами, существует линейная комбинация \((1,2,6)\) и \((-1,2,-1)\), равная \((8,16,3)\). Мы можем визуализировать последнее утверждение геометрически. Таким образом, на следующем рисунке \(\PageIndex{1}\) дана оценка картина согласованной системы уравнений . Сравните с Рисунок \(\PageIndex{2}\), на котором показана картина несогласованной системы.
Эквивалентно, это означает, что приведенное выше векторное уравнение имеет решение. Другими словами, существует линейная комбинация \((1,2,6)\) и \((-1,2,-1)\), равная \((8,16,3)\). Мы можем визуализировать последнее утверждение геометрически. Таким образом, на следующем рисунке \(\PageIndex{1}\) дана оценка картина согласованной системы уравнений . Сравните с Рисунок \(\PageIndex{2}\), на котором показана картина несогласованной системы.
Для решения векторного уравнения
\[x\color{Red}{\left(\begin{array}{c}1\\2\\6\end{array}\right)} \color{ black}{+y}\color{Green}{\left(\begin{array}{c}-1\\-2\\-1\end{array}\right)}\color{black}{=} \color{blue}{\left(\begin{array}{c}8\\16\\3\end{array}\right)}\color{black}{,}\nonumber\]
надо решить систему линейных уравнений
\[\left\{\begin{array}{rrrrc} x &-& y &=& 8\\ 2x &-& 2y &=& 16\\ 6x &-& y &=& 3. \end{массив}\right. \nonumber\]
\end{массив}\right. \nonumber\]
Это означает формирование расширенной матрицы
\[\left(\begin{array}{cc|c}\color{Red}{1}&\color{Green}{-1}&\color {синий}{8} \\ \color{красный}{2}&\color{зеленый}{-2}&\color{синий}{16}\\ \color{красный}{6}&\color{зеленый }{-1} &\color{blue}{3}\end{массив}\right)\nonnumber\]
и уменьшение ряда. Обратите внимание, что столбцы расширенной матрицы являются векторами из исходного векторного уравнения , поэтому на самом деле нет необходимости записывать систему уравнений: можно напрямую перейти от векторного уравнения к расширенной матрице, «сложив векторы вместе». ». В примере \(\PageIndex{1}\) мы выполняем сокращение строк и находим решение.
Пример \(\PageIndex{1}\)
Является ли \(\left(\begin{array}{c}8\\16\\3\end{array}\right)\) линейной комбинацией \ (\left(\begin{array}{c}1\\2\\6\end{массив}\right)\) и \(\left(\begin{array}{c}-1\\-2\ \-1\конец{массив}\справа)\)?
Решение
Как обсуждалось выше, этот вопрос сводится к сокращению строки:
\[\left(\begin{array}{cc|c} 1&-1&8 \\ 2&-2&16 \\ 6&-1&3\end {массив}\right) \quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&-1 \\ 0&1&-9 \\ 0&0&0\end{массив}\right ). \nonumber\]
\nonumber\]
Из этого мы видим, что уравнение непротиворечиво, и решение имеет вид \(x=-1\) и \(y=-9\). Мы заключаем, что \(\left(\begin{array}{c}8\\16\\3\end{array}\right)\) действительно является линейной комбинацией \(\left(\begin{array}{ c}1\\2\\6\end{массив}\right)\) и \(\left(\begin{array}{c}-1\\-2\\-1\end{массив}\right )\), с коэффициентами \(-1\) и \(-9n\) и \(x_1,x_2,\ldots,x_k\) — неизвестные скаляры, имеет тот же набор решений, что и линейная система с расширенной матрицей
\[\left(\begin{array}{cccc|c} | & |&\quad &|&| \\ v_1 &v_2 &\cdots &v_k &b \\ |&|&\quad &|&|\end{array}\right)\nonumber\]
, чьи столбцы являются \( v_i\) и \(b\)’s.
Теперь у нас есть три эквивалентных способа представить линейную систему:
- Как систему уравнений:
\[\left\{\begin{array}{rrrrrrr} 2x_1 &+& 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{массив}\right .\номер\] - В виде расширенной матрицы:
\[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonnumber\] - В виде векторного уравнения (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
\[x_{1}\left(\begin{array}{c}2\\1\end{array}\ вправо)+x_{2}\влево(\begin{массив}{c}3\\-1\конец{массив}\вправо)+x_{3}\влево(\begin{массив}{c}-2\ \-3\end{массив}\right)=\left(\begin{массив}{c}7\\5\end{массив}\right)\nonnumber\] 9н\). Диапазон из \(v_1,v_2,\ldots,v_k\) представляет собой набор всех линейных комбинаций \(v_1,v_2,\ldots,v_k\text{,}\) и обозначается \(\ text{Span}\{v_1,v_2,\ldots,v_k\}\). В символах:
Диапазон из \(v_1,v_2,\ldots,v_k\) представляет собой набор всех линейных комбинаций \(v_1,v_2,\ldots,v_k\text{,}\) и обозначается \(\ text{Span}\{v_1,v_2,\ldots,v_k\}\). В символах:\[ \text{Span}\{v_1,v_2,\ldots,v_k\} = \bigl\{x_1v_1 + x_2v_2 + \cdots + x_kv_k \mid x_1,x_2,\ldots,x_k \text{ in }\mathbb{R}\bigr\} \nonumber \]
Мы также говорим, что \(\text{Span}\{v_1,v_2,\ldots,v_k\}\) — это подмножество , натянутое на или генерируется векторами \(v_1,v_2,\ldots,v_k\).
Приведенное выше определение Definition \(\PageIndex{2}\) является первым из нескольких основных определений , которые мы встретим в этом учебнике. Они важны в том смысле, что составляют сущность предмета линейной алгебры: изучение линейной алгебры означает (частично) изучение этих определений. Все определения важны, но очень важно, чтобы вы выучили и поняли определения, помеченные как таковые.

Примечание \(\PageIndex{3}\): Установить нотацию Builder
Нотацию
\[ \bigl\{x_1v_1 + x_2v_2 + \cdots + x_kv_k \mid x_1,x_2,\ldots,x_k \text{ в }\mathbb{R}\bigr\} \nonumber \]
читается как: «множество всех вещей вида \(x_1v_1 + x_2v_2 + \cdots + x_kv_k\), таких что \(x_1,x_2,\ldots ,x_k\) находятся в \(\mathbb{R}\)». Вертикальная черта – «такая, что»; все, что слева от него, — это «множество всех вещей этой формы», а все, что справа, — это условие, которому эти вещи должны удовлетворять, чтобы быть в множестве. Задание набора таким образом называется установить обозначение построителя .
Все математические обозначения являются лишь стенографическими: любая последовательность символов должна переводиться в обычное предложение.
Примечание \(\PageIndex{4}\): три характеристики согласованности
Теперь у нас есть три эквивалентных способа сделать одно и то же утверждение:
- Вектор \(b\) находится в промежутке \(v_1, v_2,\ldots,v_k\).

- Векторное уравнение
\[x_1 v_1 +x_2 v_2 +\cdots +x_k v_k =b\nonnumber\]
имеет решение. - Линейная система с расширенной матрицей
\[\left(\begin{array}{cccc|c} |&|&\quad &|&| \\ v_1 &v_2 &\cdots &v_k &b \\ |&|&\quad &|&| \end{массив}\right)\nonumber\]
соответствует.
Эквивалент означает, что для любого заданного списка векторов \(v_1,v_2,\ldots,v_k,\,b\text{,}\) либо все три утверждения верны, либо все три утверждения ложны .
Рисунок \(\PageIndex{2}\): Это изображение несовместимая линейная система: вектор \(w\) в правой части уравнения \(x_1v_1 + x_2v_2 = w\) не лежит в промежутке \(v_1,v_2\). Убедитесь в этом сами, попробовав решить уравнение \(x_1v_1 + x_2v_2 = w\) путем перемещения ползунков и сокращения строк. Сравните это с рисунком \(\PageIndex{1}\).Фотографии пролетов.
Рисование изображения \(\text{Span}\{v_1,v_2,\ldots,v_k\}\) аналогично рисованию всех линейных комбинаций \(v_1,v_2,\ldots,v_k\ ).
 93\). Установите флажок «Показать x.v + y.w + z.u» и переместите ползунки, чтобы увидеть, как каждая точка в фиолетовой области на самом деле является линейной комбинацией трех векторов.
93\). Установите флажок «Показать x.v + y.w + z.u» и переместите ползунки, чтобы увидеть, как каждая точка в фиолетовой области на самом деле является линейной комбинацией трех векторов.Эта страница под названием 2.2: Vector Equations and Spans распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Дэном Маргалитом и Джозефом Рабинофф с помощью исходного содержимого, которое было отредактировано в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэн Маргалит и Джозеф Рабинофф
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Теги
- источник@https://textbooks.
 math.gatech.edu/ila
math.gatech.edu/ila
- источник@https://textbooks.
Подкаст FYPC, выпуск 26: Дэн Касетта, руководитель отдела продаж компании Vector Marketing и Cutco Cutlery0065 Дэн Касетта — человек эпохи Возрождения. Менеджер по продажам с более чем 30-летним стажем работы в Vector Marketing и Cutco Cutlery, национальный спикер, автор бестселлеров и ведущий подкаста «Changing Lives Selling Knives Podcast», Дэн страстно любит соединять хорошие идеи и замечательных людей.
Дэн также проводит мероприятия, объединяющие предпринимателей, лидеров и продавцов в качестве бизнес-тренера и тренера по жизни.
«Я думаю, важно восхищаться людьми и проявлять к ним искренний интерес», — сказал Дэн.
Узнайте, как Дэн преследует свою любимую карьеру в подкасте Find Your Passion Career Podcast!
Дэн начал свою увлеченную карьеру «с места в карьер», еще будучи студентом Университета Санта-Клары. Сначала он думал, что будет специалистом по финансам. Но вскоре он обнаружил в себе страсть к работе с людьми во время занятий по менеджменту и свой ранний опыт работы с Vector Marketing и Cutco Cutlery.

Дэн понял, что его тянет к должностям, которые позволяют ему продвигать себя в погоне за практически неограниченным доходом и свободой в составлении собственного графика.
Теперь, будучи региональным менеджером Западного региона компании Vector, он управляет повседневными операциями, работая с восемью руководителями подразделений и сотнями торговых представителей. Даже в этот напряженный рабочий день Дэн находит время для постоянного обучения.
Постоянное обучение
«Я чувствую, что некоторая форма личного развития очень важна на регулярной основе, если не на ежедневной основе», — сказал Дэн.
Дэн делает это, читая, слушая подкасты и просматривая видео. Затем он ставит точку, чтобы поделиться своими новыми знаниями.
«Обмен тем, что я узнаю в разных контекстах, с разной аудиторией, дает мне возможность усвоить то хорошее, что я узнаю. Так что я делаю это в первую очередь через письмо, но также и через выступления, а затем, конечно же, все мероприятия, которые я провожу в рамках своего бизнеса Cutco».

Но вам не обязательно быть оратором, чтобы изучать и усваивать информацию. Или даже на руководящей должности, если на то пошло. Простое письмо может помочь вам организовать свои мысли и поразмышлять над тем, что вы узнали. «Каждый должен каким-то образом писать, будь то ведение дневника или что-то более публичное, например блог, просто для того, чтобы иметь возможность выбросить свои идеи из головы и дать себе возможность повторить эти идеи», — сказал Дэн.
Дэн также считает, что «связи — это ресурсы». Он рассматривает создание вашей сети как еще один важный аспект личного развития.
Этот процесс не происходит в одночасье, а скорее включает в себя постепенный поиск и открытость для настоящих связей. И они могут прийти из неожиданного места.
«Каждый день вы начинаете с осознания того, что тот, кого вы встретите сегодня, может оказать глубокое влияние на всю оставшуюся жизнь. И если вы начнете с этого осознания в начале дня, вы будете лучшим в этот день…» — сказал Дэн.

Дэн призывает нас делать обдуманный выбор при расширении вашей сети от открытой до общения в чате с кем-то в очереди или даже инвестирования в посещение выступления. Он верит в силу окружить себя людьми, которые разделяют вашу страсть. В 19 лет Дэн заплатил 600 долларов, чтобы посетить мероприятие Тони Роббинса, где он услышал о Джиме Роне, известном американском предпринимателе, писателе и спикере. Дэн был вдохновлен и знал, что хочет пойти по стопам Рона, поскольку он продолжал посещать эти мероприятия и в конечном итоге даже сам стал спикером.
Добавление ценности
В подкасте Дэн объясняет, что он считает важным аспектом увлеченной карьеры: добавление ценности. «Вы должны найти какое-то занятие, где вы можете принести пользу другим, и вы будете знать, что добавляете ценность, потому что если вы это делаете, вам платят».
Где вы можете повысить ценность, преследуя свою страсть ? Возьмите записку от Дэна и будьте очарованы окружающими. Спросите их об их увлечениях.

- Вектор \(b\) находится в промежутке \(v_1, v_2,\ldots,v_k\).


 Найти длину отрезка TS.
Найти длину отрезка TS. (1185)
(1185) ..
..
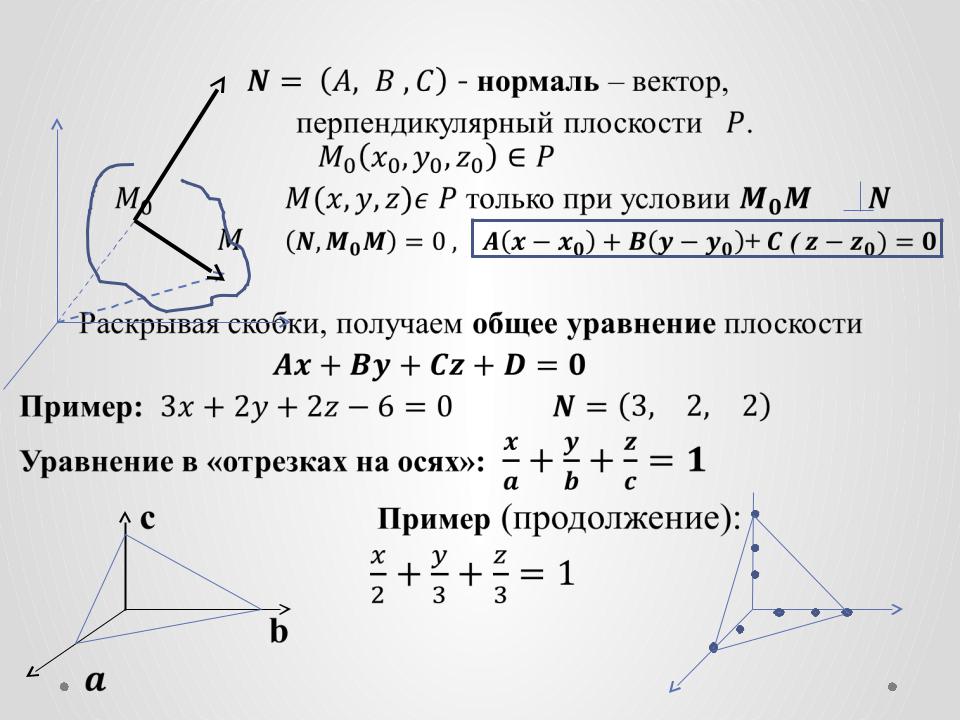
 Сразу извиняюсь, если где ошибся =)
Сразу извиняюсь, если где ошибся =) В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».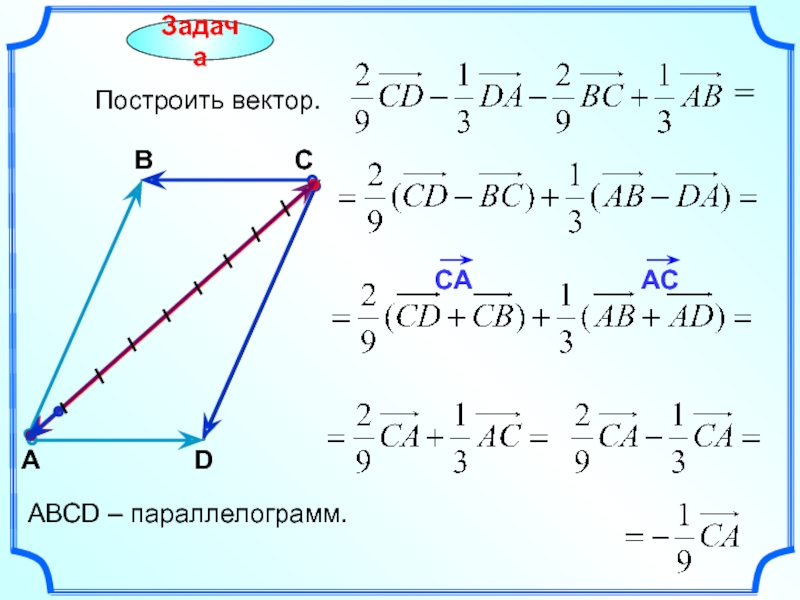 Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
 Вектор можно переместить в любую точку плоскости.
Вектор можно переместить в любую точку плоскости.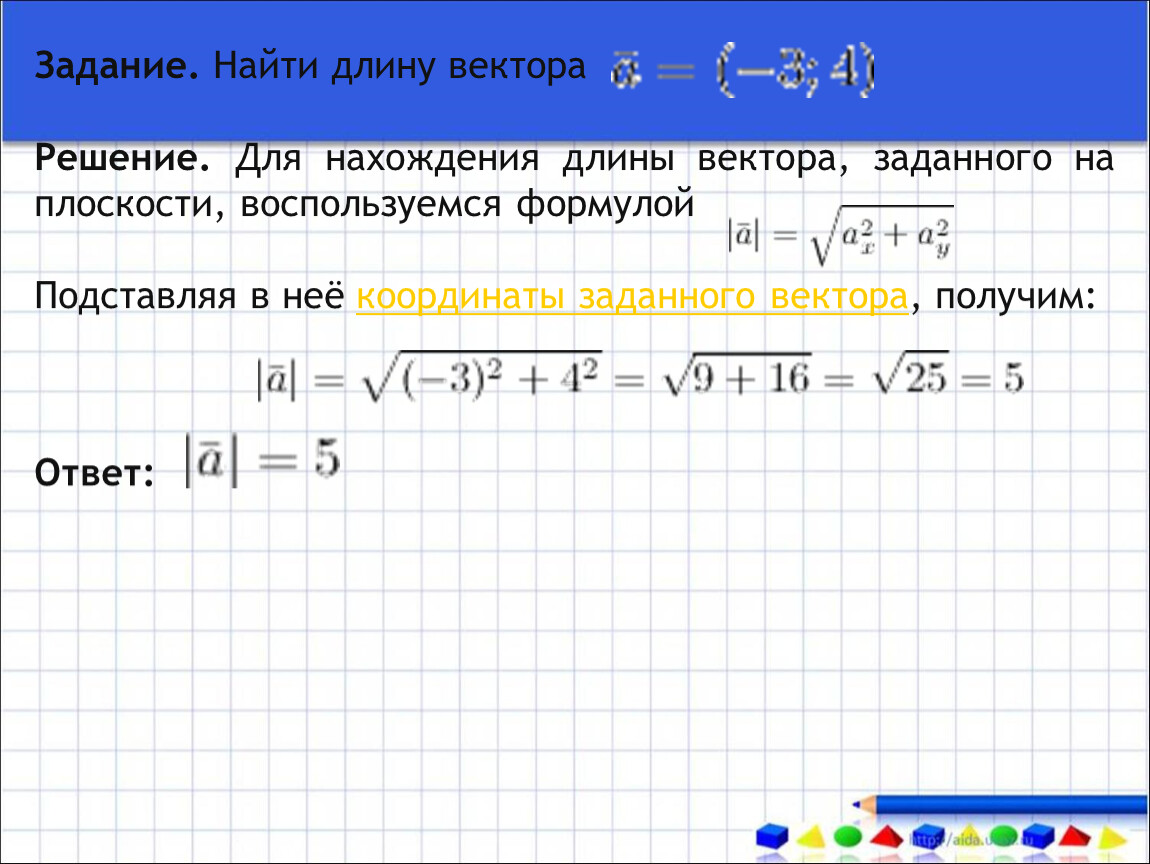 ..
.. 3\).
3\). Диапазон из \(v_1,v_2,\ldots,v_k\) представляет собой набор всех линейных комбинаций \(v_1,v_2,\ldots,v_k\text{,}\) и обозначается \(\ text{Span}\{v_1,v_2,\ldots,v_k\}\). В символах:
Диапазон из \(v_1,v_2,\ldots,v_k\) представляет собой набор всех линейных комбинаций \(v_1,v_2,\ldots,v_k\text{,}\) и обозначается \(\ text{Span}\{v_1,v_2,\ldots,v_k\}\). В символах:

 93\). Установите флажок «Показать x.v + y.w + z.u» и переместите ползунки, чтобы увидеть, как каждая точка в фиолетовой области на самом деле является линейной комбинацией трех векторов.
93\). Установите флажок «Показать x.v + y.w + z.u» и переместите ползунки, чтобы увидеть, как каждая точка в фиолетовой области на самом деле является линейной комбинацией трех векторов. math.gatech.edu/ila
math.gatech.edu/ila


