Дан закон распределения дискретной случайной величины х: Математическое ожидание случайной величины. Подробный пример решения

Дан закон распределения дискретной случайной величины:

X	1	2	3	4	5
P	0,45	0,28	0,22	0,04	0,01

Математическое ожидание данной случайной величины равно:

1. 2.95

2. 1.88

3. 3.75

4. 4,15

27. Дан закон распределения дискретной случайной величины:

X	1	2	3	4	5
P	0,45	0,28	0,22	0,04	0,01

дисперсия данной случайной величины равна:

1. 2. 95.

2. 1.19

3. 3.75

4. 4,15

28. Дан закон распределения дискретной случайной величины:

X	2	4	6
P	0,3	0,1	0,6

Математическое ожидание:

1. 7,6

2. 2,7

3. 3,6

4. * 4,6

29. Случайная дискретная величина принимает три возможных значения: x₁=4 с вероятностью p₁=0.5; x₂=6 с вероятностью p₂=0,3 и x₃ с вероятностью p₃. Значения x₃ и p₃ при M(X)=8:

1. x3=12; p3=0,2

2. x3=18; p3=0,1

3. x3=21; p3=0,2

4. x3=20; p3=0,3

30. Случайная дискретная величина принимает три возможных значения: x₁=4 с вероятностью p₁=0.5; x₂=6 с вероятностью p₂

    =0,3 и x₃ с вероятностью p3. Значения x₃ и p₃, при M(X)=8.

1. x3=12; p3=0,2

2. x3=18; p3=0,1

3. x3=21; p3=0,2

4. x3=20; p3=0,3

31. Дан перечень возможных значений дискретной случайной величины X: x₁=2, x₂=4, а также известно ее математическое ожидание M(X)=3 . Значения p₁, p₂, соответствующие возможным значениям x₁, x₂:

1. p1=0,4; p2=0,6

2. p1=0,3; p2=0,7

3. p1=0,5; p2=0,5

4. p1=0,2; p2=0,8

32. Дан закон распределения дискретной случайной величины

X	1	2	3	4
p	0,2	0,4	0,1	0,3

P(X<3) = …

33. Дан закон распределения дискретной случайной величины X:

X	1	3	5	7
p	0,3	0,1	0,2	p4

Значения p₄ и P(X<7):

1. p4=0,5; P(X<7)=0,4

2. p4=0,4; P(X<7)=0,3

3. p4=0,3; P(X<7)=0,6

4. p4=0,4; P(X<7)=0,5

34. Закон распределения вероятностей дискретной случайной величины

3. 

35. Пропущенное значение вероятности в законе распределения дискретной случайной величины c математическим ожиданием M(X)=3 равно …

    xi	1	3	4
    pi	0,5	0,1	0,2

36. Пропущенное значение x₄ в законе распределения дискретной случайной величины c математическим ожиданием M(X)=3 равно …

    xi	1	3	4
    pi	0,5	0,1	0,2

37. Даны числовые характеристики двух случайных величин X и Y: MX=3, MY=7, DX=1, DY=2.

    Значение M(3X+2Y):

    1. 23;

    2. 21

    3. 25

    4. 28

38. Даны числовые характеристики двух случайных величин X и Y: MX=3, MY=7, DX=1, DY=2. Значение D(4X-Y).

    1. 2

    2. 14

    3. 15

    4. 18

39. Два стрелка независимо друг от друга стреляют по одной цели. Вероятность попадания в цель первого стрелка равна 0,7; второго – 0,8. Математическое ожидание числа попаданий в цель:

    1. 1,5

    2. 0,7

    3. 0,8

    4. 1,4

40. Дана функция распределения случайной величины

F(x)=

.

Математическое ожидание X равно:

1. 1;

2. 3;

3. 2;

4. 2,5.

41. Соответствие между формулой и определением

Математическое ожидание дискретной случайной величины	A.
Математическое ожидание константы	B. с
Математическое ожидание суммы случайных величин	C.

42. Соответствие между формулой и определением

Дисперсия дискретной случайной величины х	A. M(x-Mx)2
Дисперсия константы	B. 0
Дисперсия произведения константы и случайной величины	C. С2Dх

43. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется … случайной величины

2.2. Непрерывные случайные величины

2.2.1. Плотность вероятности и интегральная функция распределения

1. С помощью плотности распределения вероятности можно задать

1. дискретную случайную величину

2. непрерывную случайную величину

3. случайное событие

4. интервальную величину

2. С помощью дифференциальной функции распределения можно задать

1. дискретную случайную величину

2. непрерывную случайную величину

3. случайное событие

4. интервальную величину

3. Вероятность каждого конкретного значения непрерывной случайной величины равна

1. 0

2. 0,1

3. 0,5

4. 1

4. Возможное событие ……. иметь нулевую вероятность

1. Может

2. Не может

3. Может для непрерывной случайной величины

4. Может для дискретной случайной величины

5. Непрерывную случайную величину можно задать с помощью

1. таблицы распределения

2. многоугольника распределения

3. функции распределения вероятности

4. плотности распределения вероятности

6. Свойства плотности вероятности

2. p (x)  0

4. p (x)  1)

5. (*)

7. Плотность вероятности любой случайной величины находится в пределах

1. от –1 до 1

2. от 0 до 1

3. от 0,5 до 1

4. от 0 до 

5. от - до 

8. Кривая, изображающая дифференциальную функцию распределения f(x) случайной величины, называется

1. полигоном распределения

2. многоугольником распределения

3. * кривой распределения

4. гистограммой

9. Случайная величина задана дифференциальной функцией распределения.

Недостающее значение a=….

10. Случайная величина задана дифференциальной функцией распределения.

Недостающее значение a=….

11. Случайная величина задана дифференциальной функцией распределения.

Недостающее значение a=….

12. Функция распределения случайной величины изменяется в интервале

1. –1 ; 1

2. 0 ; 1

3. 0,5 ; 1

4. 0 ; –1

13. Случайная величина X задана функцией распределения

F(x)=.

Вероятность того, что случайная величина X примет значение, принадлежащее интервалу (0,25;0,75) равна:

1. 0,5;

2. 0,25;

3. 0,375;

4. 0,475

5. 458.

1. Cвойство, не обязательное для функции распределения:

1. F(X) не более 1

2. F(X) не убывает с ростом х

3. F(0)=0

4. F(X) не отрицательна

15. Дискретно-непрерывная случайная величина может быть задана в виде

1. интегральной функции распределения

2. дифференциальной функции распределения

3. полигона частот

4. таблицы

16. Непрерывная случайная величина может быть задана в виде

1. интегральной функции распределения

2. таблицы

3. дифференциальной функции распределения

4. полигона частот

5. гистограммы

17. Дифференциальная функция распределения представляет собой зависимость … вероятности случайной величины от значения этой случайной величины

18. Знак в выражении для интегральная функции распределения F(x) = P(X … x)

1. 

2. 

3. 

4. 

5. =

19. Функция распределения любой случайной величины имеет значения в интервале

1. (-1;)

2. (-1;0)

3. (-1;1)

4. (0;1)

5. (0; )

20. Функция распределения случайной величины F(x). Интеграл в бесконечных пределах от плотности распределения вероятности равен\

1. 1

2. 0

3. 0,5

4. F()

5. F(0)

21. Вероятность любого отдельного значения непрерывной случайной величины равна

1. 1

2. 0

3. 0,5

4. F()

5. -1

22. Cвойство, не обязательное для многомерной функции распределения:

1. F(X) не отрицательна

2. F(X) не убывает с ростом любого из ее аргументов

3. Не имеет разрывов

4. Не превосходит 1

23. Дана плотность вероятности непрерывной случайной величины:

f(x)=;

Величина А равна:

1. a=2;

2. a=1;

3. a=3;

4. a=2,5

24. Дана плотность вероятности непрерывной случайной величины:

f(x)=;

MX равно:

1. MX=0,75;

2. MX=0,6;

3. MX=0,75;

4. MX=0,78.

25. Дана плотность вероятности непрерывной случайной величины X:

f(x)=;

P(0,1<X<0,3) равна:

1. P(0,1<X<0,3)=0,026;

2. P(0,1<X<0,3)=0,25;

3. P(0,1<X<0,3)=0,26;

4. P(0,1<X<0,3)=0,03.

26. Дана плотность вероятности непрерывной случайной величины X:

f(x)=.

Вероятность P(1<X<3) равна:

1. P(1<X<3)=0,6;

2. P(1<X<3)=0,55;

3. P(1<X<3)=0,5;

4. P(1<X<3)=0,4.

27. Дана плотность вероятности случайной величины X:

f(x)=.

Величина А равна:

1. A=1;

2. A=1/2;

3. A=2;

4. A=3/2.

28. Дана плотность вероятности случайной величины X:

f(x)=.

Вероятность P(5<X<7) равна:

1. 0,5;

2. 0,25;

3. -0,5;

4. 1.

29. Непрерывная случайная величина X имеет плотность . Вероятность попадания случайной величины X на участок от 0 до :

1. 1/2

3. 1/3

5. 2/3

30. F(x) — функция распределения центрированной, симметрично распределенной непрерывной случайной величины X. Справедливы равенства:

1. P(x≥0) = F(-)

2. P(x≥0) = F(0) (*)

3. P(x≥0) = F()

4. P(x≥0) = 1-F(0)

5. P(x≥0) = F()-F(0)

31. Соответствие между величинами для непрерывной стандартной симметрично распределенной случайной величины X:

p(-x)	p(x)
F(-X)	1-F(x)
M(X)	0
D(X)	1

2. 2.2. Числовые характеристики случайных величин

Математическое ожидание непрерывной случайной величины

Дисперсия непрерывной случайной величины х равна

3. Дан закон распределения дискретной случайной величины:

X	1	2	3	4
p	0,4	0,35	0,15	0,1

Математическое ожидание данной случайной величины равно:

1. 1. 95.

2. 2.95.

3. 2.09

4. 3.75

1. Дан закон распределения дискретной случайной величины:

X	1	2	3	4
p	0,4	0,35	0,15	0,1

Дисперсия данной случайной величины равна:

1. 2.95.

2. 2.09

3. 3.75

4. 0,95

5. Дан закон распределения дискретной случайной величины:

X	1	2	3	4
p	0,4	0,35	P3	0,1

Значение P₃ равно

1. 0,95

2. 0,09

3. 0,75

4. 0,15

6. Дана плотность вероятности непрерывной случайной величины X:

f(x)=.

Математическое ожидание MX равно:

1. MX=2

2. MX=3

3. MX=8/3

4. MX=7/3

7. Соответствие между формулой и определением

Вероятность того, что непрерывная случайная величина ξ примет значение, лежащее в интервале (а,b) равна
Математическое ожидание непрерывной случайной величины определяется по формуле
Дисперсия непрерывной случайной величины х равна

8. Независимые случайные величины X и Y распределены равномерно в интервалах соответственно [-1 ; 1] и [2 ; 4]. Математическое ожидание и дисперсия их суммы

1. М(х+y)=3; D(x+y)=2/3

2. М(х+y)=3; D(x+y)=2/9

3. М(х+y)=3; D(x+y)=1/12

4. М(х+y)=1; D(x+y)=2/3

9. Свойства математического ожидания

1. M (cX) = c M(X)

2. M (c) = 0

3. M (c) = c

4. M (X+Y) = M (X) + M(Y)

5. M (X+Y) = M (X) + M(Y) – M(XY)

10. Дисперсия произвольной случайной величины X описывается выражением

2. (*)

3. (*)

11. Дисперсия разности независимых случайных величин равна

1. Разности их дисперсий

2. Сумме их дисперсий

3. Дисперсии их произведения

12. Математическое ожидание разности независимых случайных величин равно

1. разности их математических ожиданий

2. сумме их математических ожиданий

3. сумме математических ожиданий минус математическое ожидание произведения

4. математическому ожиданию их произведения

13. Третий центральный момент случайной величины характеризует

1. среднее значение

2. островершинность распределения

3. асимметрию распределения

4. Разброс значений относительно математического ожидания

14. Четвертый центральный момент случайной величины характеризует

1. ее среднее значение

2. островершинность распределения

3. асимметрию распределения

4. Разброс значений относительно математического ожидания

15. Второй центральный момент случайной величины характеризует

1. ее среднее значение

2. островершинность распределения

3. асимметрию распределения

4. разброс значений относительно математического ожидания

16. Первый начальный момент случайной величины представляет собой

1. математическое ожидание случайной величины

2. дисперсию случайной величины

3. среднее значение случайной величины

4. среднее квадратическое отклонение случайной величины

17. Значения среднего квадратического отклонения, начальных _i и центральных _i моментов стандартизованной случайной величины

1.  ₃ = 0

2. ₁ = 0

3.  = 1

4.  ₂ = 1

5.  ₄ /  ⁴ = 3

2.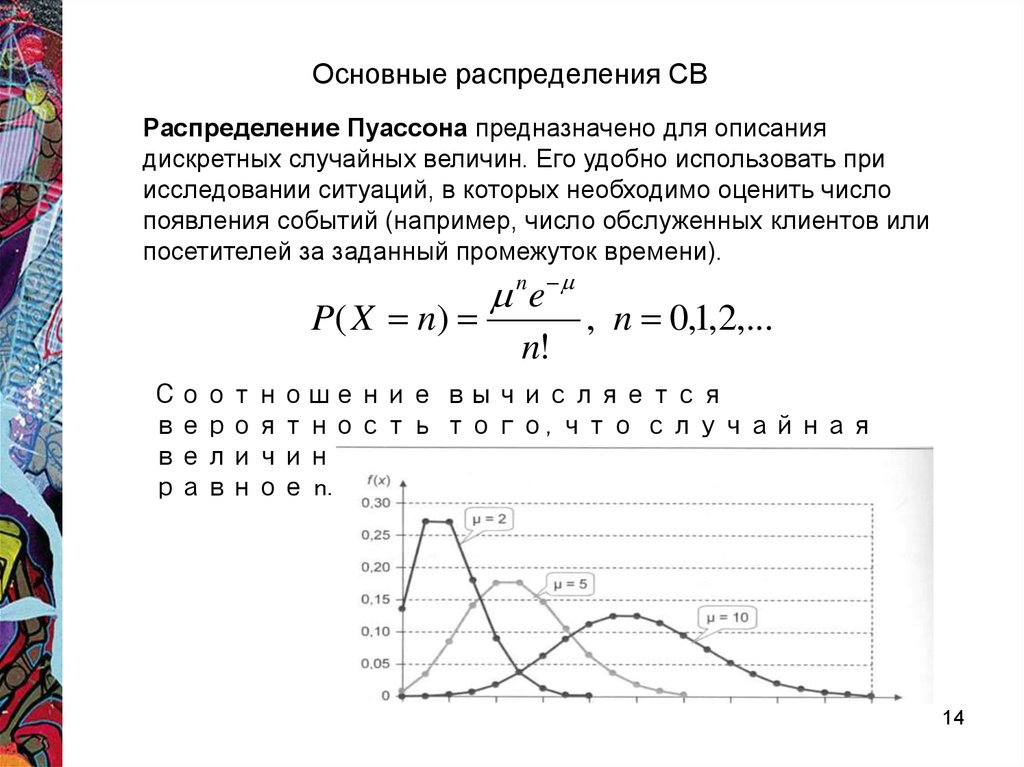 3. Законы распределения вероятностей

2.3.1. Нормальный закон распределения

1. Нормированный нормальный закон распределения вероятностей:

Математическое ожидание нормального распределения равно	a
	(b+a)/2
	np
	m/n
	npq

	a
Дисперсия нормального закона распределения равна
	np
	m/n
	npq

1.

Дан закон распределения дискретной случайной величины

	1	3	11	500
	0,3	0,4

Известно, что . Найти , , , .

2. Бросают кубик до выпадения первой «тройки», но не более, чем 5 раз. Х — число бросаний кубика. Выписать закон распределения дискретной случайной величины Х. Найти

3. Произвели 5 испытаний, в каждом из которых вероятность наблюдать событие равна 0,2.

Х – количество испытаний, в которых событие A наблюдалась. Выписать закон распределения дискретной случайной величины Х. Найти

5. Случайная величина распределена по биномиальному закону. Известно, что ее математическое ожидание равно 2,4, дисперсия равна 0,92. Найти вероятность того, что .

Вариант 14.

1. Дан закон распределения дискретной случайной величины

	-1	1	3	300
	0,2	0,2

Известно, что . Найти , , , .

2. Магазин получает от фабрики партии товара. Следующая партия получается только в случае продажи предыдущих. Вероятность продажи первой партии равна 0,7; для каждой последующей эта вероятность уменьшается на 0,2. Х – количество полученных тонн товара. В 1-ой партии – 500 тонн, во 2-ой – 200 тонн, в 3-ей – 150, в 4-ой – 100, в 5-ой -50. Выписать закон распределения дискретной случайной величины Х. Найти

3. В потоке вагонов, идущем на сортировочную горку 30% шестиосные и 70% четырехосные.

Х – количество шестиосных в отцепе из 4 вагонов. Выписать закон распределения дискретной случайной величины Х. Найти

5. Случайная величина распределена по закону Пуассона. Известно, что . Найти вероятность, что .

_______________________________________________________________________________________

Вариант 15.

1. Дан закон распределения дискретной случайной величины

	1	3	100	700
	0,4	0,1

Известно, что . Найти , , , .

2. Студент сдает экзамены по математике, информатике и литературе. Вероятность сдать математику равна 0,7; информатику – 0,4. Если студент сдал хотя бы один экзамен, вероятность сдать литературу – 0,9; в ином случае – 0,3.

Х – число сданных экзаменов. Найти

3. Кубик бросили 5 раз. Х – количество бросаний, при которых выпадало нечетное число очков. Выписать закон распределения дискретной случайной величины Х. Найти

5. Случайная величина распределена по биномиальному закону. Известно, что ее математическое ожидание равно 2,8, дисперсия равна 1,68. Найти вероятность того, что .

Вариант

1. Дан закон распределения дискретной случайной величины

	-1	1	3	500
	0,2	0,2

Известно, что . Найти , , , .

2. Комиссар Жюв с помощниками устроили 3 хитроумные ловушки на Фантомаса. Однако Фантомас не прост: первую ловушку он проходит с вероятностью 0,5; для каждой последующей ловушки эта вероятность уменьшается на 0,2. Х — число пройденных злодеем ловушек. Выписать закон распределения дискретной случайной величины Х. Найти

3. Дана функция плотности вероятности

Найти .

4. Случайная величина распределена по нормальному закону с параметрами и , , Найти .

Статистика | Определение, типы и значение

гистограмма

Посмотреть все СМИ

Ключевые люди:

Карл Пирсон Сэр Рональд Эйлмер Фишер Молли Оршанский Ричард фон Мизес ПК. Махаланобис

Похожие темы:

Парадокс Симпсона кластерный анализ регрессия к среднему шкала измерения закон больших чисел

Просмотреть весь связанный контент →

статистика , наука о сборе, анализе, представлении и интерпретации данных. Потребность правительства в данных переписи, а также в информации о различных видах экономической деятельности во многом послужила толчком для развития области статистики на раннем этапе. В настоящее время необходимость превращения больших объемов данных, доступных во многих прикладных областях, в полезную информацию стимулировала как теоретические, так и практические разработки в статистике.

Данные — это факты и цифры, которые собираются, анализируются и обобщаются для представления и интерпретации. Данные могут быть классифицированы как количественные или качественные. Количественные данные измеряют количество или количество чего-либо, а качественные данные предоставляют ярлыки или имена для категорий подобных предметов. Например, предположим, что конкретное исследование интересует такие характеристики, как возраст, пол, семейное положение и годовой доход для выборки из 100 человек. Эти характеристики будут называться переменными исследования, и значения данных для каждой из переменных будут связаны с каждым человеком. Таким образом, значения данных 28, мужчина, холост и 30 000 долларов будут записаны для 28-летнего холостого мужчины с годовым доходом 30 000 долларов. При наличии 100 человек и 4 переменных набор данных будет состоять из 100 × 4 = 400 элементов. В этом примере возраст и годовой доход являются количественными переменными; соответствующие значения данных указывают, сколько лет и сколько денег для каждого человека. Пол и семейное положение являются качественными переменными. Ярлыки «мужской» и «женский» предоставляют качественные данные о поле, а ярлыки «холост», «замужем», «разведен» и «овдовевший» указывают на семейное положение.

Методы выборочного обследования используются для сбора данных обсервационных исследований, а методы планирования эксперимента используются для сбора данных экспериментальных исследований. Область описательной статистики связана в первую очередь с методами представления и интерпретации данных с использованием графиков, таблиц и числовых сводок. Всякий раз, когда статистики используют данные из выборки, т. е. подмножества совокупности, чтобы делать выводы о совокупности, они выполняют статистический вывод. Оценка и проверка гипотезы — это процедуры, используемые для получения статистических выводов. Такие области, как здравоохранение, биология, химия, физика, образование, инженерия, бизнес и экономика, широко используют статистические выводы.

Вероятностные методы первоначально были разработаны для анализа азартных игр. Вероятность играет ключевую роль в статистическом выводе; он используется для измерения качества и точности выводов. Многие из методов статистического вывода описаны в этой статье. Некоторые из этих методов используются в основном для исследований с одной переменной, в то время как другие, такие как регрессионный и корреляционный анализ, используются для получения выводов о взаимосвязях между двумя или более переменными.

Линейные, столбчатые и свечные графики: технические аналитики используют три типа

Описательная статистика представляет собой табличные, графические и числовые сводки данных. Цель описательной статистики — облегчить представление и интерпретацию данных. Большинство статистических материалов, публикуемых в газетах и ​​журналах, носят описательный характер. Одномерные методы описательной статистики используют данные для улучшения понимания одной переменной; многомерные методы сосредоточены на использовании статистики для понимания взаимосвязей между двумя или более переменными. Чтобы проиллюстрировать методы описательной статистики, рассмотрим предыдущий пример, в котором были собраны данные о возрасте, поле, семейном положении и годовом доходе 100 человек.

Табличные методы

Наиболее часто используемая табличная сводка данных для одной переменной представляет собой частотное распределение. Распределение частоты показывает количество значений данных в каждом из нескольких непересекающихся классов. Другая табличная сводка, называемая относительным частотным распределением, показывает долю или процент значений данных в каждом классе. Наиболее распространенная табличная сводка данных для двух переменных представляет собой перекрестную таблицу, аналог частотного распределения с двумя переменными.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Для качественной переменной частотное распределение показывает количество значений данных в каждой качественной категории. Например, переменная «пол» имеет две категории: «мужской» и «женский». Таким образом, частотное распределение по полу будет иметь два непересекающихся класса, чтобы показать количество мужчин и женщин. Распределение относительной частоты для этой переменной покажет долю лиц мужского пола и долю лиц женского пола.

Построение частотного распределения для количественной переменной требует большей осторожности при определении классов и точек разделения между соседними классами. Например, если возрастные данные в приведенном выше примере находятся в диапазоне от 22 до 78 лет, можно использовать следующие шесть непересекающихся классов: 20–29, 30–39, 40–49, 50–59, 60–69 и 70–70 лет. 79. Распределение частоты покажет количество значений данных в каждом из этих классов, а распределение относительной частоты покажет долю значений данных в каждом из этих классов.

Перекрестная таблица представляет собой двустороннюю таблицу, в которой строки таблицы представляют классы одной переменной, а столбцы таблицы представляют классы другой переменной. Чтобы построить перекрестную таблицу с использованием переменных «пол» и «возраст», пол можно показать в двух строках, мужской и женский, а возраст можно показать в шести столбцах, соответствующих возрастным классам 20–29, 30–39, 40–49, 50 лет. –59, 60–69 и 70–79. Запись в каждой ячейке таблицы будет указывать количество значений данных с полом, указанным в заголовке строки, и возрастом, указанным в заголовке столбца. Такая перекрестная таблица может быть полезна для понимания взаимосвязи между полом и возрастом.

Для описания данных доступно несколько графических методов. Гистограмма — это графическое устройство для изображения качественных данных, которые были суммированы в частотном распределении. Метки категорий качественной переменной показаны на горизонтальной оси графика. Полоса над каждой меткой построена таким образом, что высота каждой полосы пропорциональна количеству значений данных в категории. Гистограмма семейного положения для 100 человек в приведенном выше примере показана на рисунке 1. На графике есть 4 столбца, по одному для каждого класса. Круговая диаграмма — еще одно графическое средство для обобщения качественных данных. Размер каждого фрагмента круговой диаграммы пропорционален количеству значений данных в соответствующем классе. Круговая диаграмма семейного положения 100 человек показана на рисунке 2.

Гистограмма является наиболее распространенным графическим представлением количественных данных, которые были суммированы в частотном распределении. Значения количественной переменной показаны на горизонтальной оси. Прямоугольник рисуется над каждым классом таким образом, что основание прямоугольника равно ширине интервала класса, а его высота пропорциональна количеству значений данных в классе.

4.2 Среднее или ожидаемое значение и стандартное отклонение

Введение

ожидаемое значение дискретной случайной величины X , обозначенное как E(X) , часто упоминается как долгосрочное среднее или среднее (обозначается как μ ). Это означает, что в течение длительного времени, проводя эксперимент снова и снова, вы должны ожидать этого среднего значения. Например, пусть X = количество выпавших орлов при подбрасывании трех одинаковых монет. Если вы повторите этот эксперимент (бросьте три честные монеты) большое количество раз, математическое ожидание X — это количество голов, которое вы ожидаете получить в среднем за каждые три броска.

ПРИМЕЧАНИЕ

Чтобы найти ожидаемое значение E(X) или среднее μ дискретной случайной величины X , просто умножьте каждое значение случайной величины на его вероятность и сложите произведения. Формула задается как E(X)=µ=∑xP(x).E(X)=µ=∑xP(x).

Здесь x представляют значения случайной величины X , P ( x ), представляет соответствующую вероятность, а символ ∑∑ представляет сумму всех произведений x P ( x ).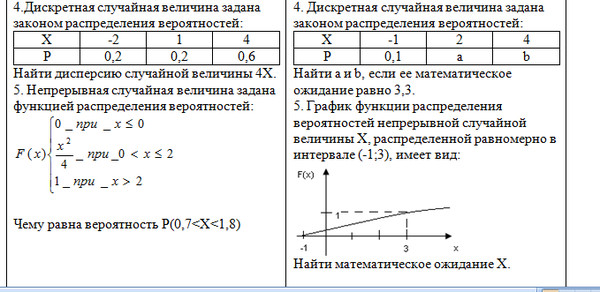 Здесь мы используем символ μ для среднего значения, потому что это параметр. Он представляет собой среднее значение населения.

Пример 4.3

Мужская футбольная команда играет в футбол ноль, один или два дня в неделю. Вероятность того, что они сыграют нулевой день, равна 0,2, вероятность того, что они сыграют один день, равна 0,5, а вероятность того, что они сыграют два дня, равна 0,3. Найдите долгосрочное среднее или ожидаемое значение, μ , количество дней в неделю, когда мужская футбольная команда играет в футбол.

Чтобы решить эту задачу, сначала пусть случайная величина X = количество дней, в течение которых мужская футбольная команда играет в футбол в неделю. X принимает значения 0, 1, 2. Создайте таблицу PDF, добавив столбец x*P(x) , произведение значения x с соответствующей вероятностью P(x) . В этом столбце вы будете умножать каждое значение x на его вероятность.

Эта таблица называется таблицей ожидаемых значений. Таблица поможет вам рассчитать ожидаемое значение или долгосрочное среднее значение.

х	Р ( х )	х * Р ( х )
0	.2	(0)(.2) = 0
1	.5	(1)(.5) = .5
2	.3	(2)(.3) = .6

Таблица 4.5 Таблица ожидаемых значений

Добавьте последний столбец x*P(x)x*P(x), чтобы получить ожидаемое значение/среднее значение случайной величины X .

E(X)=µ=∑xP(x)=0+.5+.6=1.1E(X)=µ=ExP(x)=0+.5+.6=1.1

Ожидаемое значение /среднее 1,1. Мужская футбольная команда в среднем будет играть в футбол 1,1 дня в неделю. Число 1,1 — это долгосрочное среднее или ожидаемое значение, если мужская футбольная команда играет в футбол неделю за неделей за неделей.

Как вы узнали из главы 3, если вы подбросите правильную монету, вероятность того, что выпадет орёл, равна 0,5. Эта вероятность является теоретической вероятностью, и мы ожидаем, что это произойдет. Эта вероятность не описывает краткосрочные результаты эксперимента. Если вы подбросите монету два раза, вероятность не говорит вам, что эти подбрасывания приведут к одному орлу и одной решке. Даже если вы подбросите монету 10 или 100 раз, вероятность не говорит вам, что выпадет половина решки и половина решки. Вероятность дает информацию о том, чего можно ожидать в долгосрочной перспективе. Чтобы продемонстрировать это, Карл Пирсон однажды подбросил правильную монету 24 000 раз! Он записал результаты каждого броска, получив орла 12 012 раз. Относительная частота выпадения орла составляет 12 012/24 000 = 0,5005, что очень близко к теоретической вероятности 0,5. В своем эксперименте Пирсон проиллюстрировал закон больших чисел.

Закон больших чисел гласит, что по мере увеличения числа испытаний в вероятностном эксперименте разница между теоретической вероятностью события и относительной частотой приближается к нулю (теоретическая вероятность и относительная частота становятся все ближе и ближе друг к другу ). Относительная частота также называется экспериментальной вероятностью, термин, который означает, что происходит на самом деле.

В следующем примере мы покажем, как найти ожидаемое значение и стандартное отклонение дискретного распределения вероятностей с использованием относительной частоты.

Как и данные, распределения вероятностей имеют дисперсию и стандартное отклонение. Дисперсия распределения вероятностей обозначается как σ2σ2, а стандартное отклонение распределения вероятностей обозначается как σ . Оба являются параметрами, поскольку они обобщают информацию о совокупности. Чтобы найти дисперсию σ2σ2 дискретного распределения вероятностей, найдите каждое отклонение от его ожидаемого значения, возведите его в квадрат, умножьте на его вероятность и сложите произведения. Чтобы найти стандартное отклонение σ распределения вероятностей, просто возьмите квадратный корень из дисперсии σ2σ2. Формулы приведены ниже.

ПРИМЕЧАНИЕ

Формула дисперсии σ2σ2 дискретной случайной величины X :

σ2=∑(x−μ)2P(x).σ2=∑(x−μ)2P(x).

Здесь x представляет значения случайной величины X , μ является средним значением X , P ( x ) представляет соответствующую вероятность, а символ ∑ представляет собой сумму всех произведений (x−μ)2P(x). (x−μ)2P(x).

Чтобы найти стандартное отклонение σ дискретной случайной величины X , просто возьмите квадратный корень из дисперсии σ2σ2.

σ=σ2=∑(x−μ)2P(x)σ=σ2=∑(x−μ)2P(x)

Пример 4.4

Исследователь провел исследование, чтобы выяснить, как плач новорожденного ребенка после полуночи влияет на сон матери ребенка. Исследователь случайным образом выбрал 50 молодых матерей и спросил, сколько раз в неделю они просыпаются от плача своего новорожденного ребенка после полуночи. Две матери проснулись ноль раз, 11 матерей проснулись один раз, 23 матери проснулись два раза, девять матерей проснулись три раза, четыре матери проснулись четыре раза и одна мать проснулась пять раз. Найдите математическое ожидание того, сколько раз в неделю плач новорожденного ребенка будит его мать после полуночи. Также вычислите стандартное отклонение переменной.

Чтобы решить задачу, сначала пусть случайная величина X = количество раз, когда мать просыпается от плача новорожденного после полуночи в неделю. X принимает значения 0, 1, 2, 3, 4, 5. Создайте таблицу PDF, как показано ниже. Столбец P ( x ) дает экспериментальную вероятность каждого значения x . Мы будем использовать относительную частоту, чтобы получить вероятность. Например, вероятность того, что мать проснется ноль раз, равна 250250, так как две матери из 50 пробуждаются ноль раз. Третий столбец таблицы представляет собой произведение значения и его вероятности, x P ( x ).

The second data row contains, 1, P opening parenthesis x = 1 closing parenthesis equals eleven fiftieths, and opening parenthesis 1 closing parenthesis opening parenthesis eleven fiftieths closing parenthesis equals eleven fiftieths. The third data row contains, 2, P opening parenthesis x = 2 closing parenthesis equals twenty-three fiftieths, and opening parenthesis 2 closing parenthesis opening parenthesis twenty-three fiftieths closing parenthesis equals forty-six fiftieths. The fourth data row contains, 3, P opening parenthesis x = 3 closing parenthesis equals nine fiftieths, and opening parenthesis 3 closing parenthesis opening parenthesis nine fiftieths closing parenthesis equals twenty-seven fiftieths. The fifth data row contains, 4, P opening parenthesis x = 4 closing parenthesis equals four fiftieths, and opening parenthesis 4 closing parenthesis opening parenthesis four fiftieths closing parenthesis equals sixteen fiftieths. The sixth data row contains, 5, P opening parenthesis x = 5 closing parenthesis equals one fiftieth, and opening parenthesis 05closing parenthesis opening parenthesis one fiftieth closing parenthesis equals five fiftieths. «>

х	Р ( х )	х Р ( х )
0	P(x = 0) = 250P(x = 0) = 250	(0)(250)=0(0)(250)=0
1	P(x = 1) =1150P(x = 1) =1150	(1)(1150)=1150(1)(1150)=1150
2	P(x = 2) = 2350P(x = 2) = 2350	(2)(2350)=4650(2)(2350)=4650
3	P(x = 3) =950P(x = 3) =950	(3)(950)=2750(3)(950)=2750
4	P(x = 4) =450P(x = 4) =450	(4)(450)=1650(4)(450)=1650
5	P(x = 5) =150P(x = 5) =150	(5)(150)=550(5)(150)=550

Таблица 4.6

Затем мы сложим все продукты в третьем столбце, чтобы получить среднее/ожидаемое значение X

E(X)=μ=∑xP(x)=0+1150+4650+2750+1650+550=10550=2,1E(X)=μ=∑xP(x)=0+1150+4650+2750 +1650+550=10550=2,1

Таким образом, мы ожидаем, что новорожденный будет будить мать после полуночи в среднем 2,1 раза в неделю.

Чтобы рассчитать стандартное отклонение σ , мы добавляем четвертый столбец ( x-μ ) ² и пятый столбец ( x-μ ) ² ∙ P ( x ), чтобы получить следующую таблицу: Р ( х ) х Р ( х ) ( х-мк ) ² ( x-µ ) ² • P ( x ) 0 Р(х=0)=250Р(х=0)=250 (0)(250)=0(0)(250)=0 (0-2,1)2=4,41(0-2,1)2=4,41 4,41•250=0,17644,41•250=0,1764 1 P(x = 1) =1150P(x = 1) =1150 (1)(1150)=1150(1)(1150)=1150 (1−2,1)2=1,21(1−2,1)2=1,21 1,21•1150=0,26621,21•1150=0,2662 2 P(x = 2) = 2350P(x = 2) = 2350 (2)(2350)=4650(2)(2350)=4650 (2−2,1)2=0,01(2−2,1)2=0,01 . 01•2350=.0046.01•2350=.0046 3 P(x = 3) =950P(x = 3) =950 (3)(950)=2750(3)(950)=2750 (3−2,1)2=0,81(3−2,1)2=0,81 0,81•950=0,1458,81•950=0,1458 4 P(x = 4) =450P(x = 4) =450 (4)(450)=1650(4)(450)=1650 (4−2,1)2=3,61(4−2,1)2=3,61 3,61•450=0,28883,61•450=0,2888 5 P(x = 5) =150P(x = 5) =150 (5)(150)=550(5)(150)=550 (5−2,1)2=8,41(5−2,1)2=8,41 8,41•150=0,16828,41•150=0,1682 Таблица 4.7

σ2=0,1764+0,2662+0,0046+0,1458+0,2888+0,1682=1,05σ2=0,1764+0,2662+0,0046+0,1458+0,2888+0,1682=1,05

Чтобы получить стандартное отклонение σ , мы просто возьмем квадратный корень из дисперсии σ ² .

σ=σ2=1,05≈1,0247σ=σ2=1,05≈1,0247

Пример 4.5

Предположим, вы играете в азартную игру, в которой выбираются пять чисел от 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Компьютер случайным образом выбирает пять чисел от нуля до девяти с замена. Вы платите 2 доллара за игру и можете получить 100 000 долларов, если угадаете все пять чисел по порядку (вы получите свои 2 доллара обратно плюс 100 000 долларов). В долгосрочной перспективе, каковы ваши ожидаемая прибыль от игры?

Чтобы решить эту задачу, создайте таблицу PDF для суммы денег, которую вы можете получить.

Пусть X = сумма денег, которую вы заработали. Если ваши пять номеров совпадут по порядку, вы выиграете игру и получите обратно свои 2 доллара плюс 100 000 долларов. Это означает, что ваша прибыль составляет 100 000 долларов. Если ваши пять номеров не совпадают по порядку, вы проиграете игру и потеряете свои 2 доллара. Это означает, что ваша прибыль составляет –$2. Следовательно, X принимает значения 100 000 долларов и -2 доллара. Это второй столбец x в таблице PDF ниже.

Чтобы выиграть, вы должны правильно угадать все пять чисел по порядку. Вероятность выбора правильного первого числа равна 110110, так как имеется 10 чисел (от нуля до девяти) и только одно из них правильное. Вероятность выбора правильного второго числа также равна 110110, потому что выбор производится с заменой и вам остается выбрать 10 номеров (от нуля до девяти). По той же причине вероятность выбора правильного третьего числа, правильного четвертого числа и правильного пятого числа также равна 110110. Выбор одного номера не влияет на выбор другого номера. Это означает, что пять выборов являются независимыми. Вероятность выбора всех пяти правильных чисел по порядку равна произведению вероятностей правильного выбора каждого числа.

P(правильный выбор всех пяти чисел)•P(правильный выбор 1-го числа)• P(правильный выбор 2-го числа)• P(правильный выбор 5-го числа)=(110)•(110)•(110)•(110) •(110)=.00001P(правильный выбор всех пяти чисел)•P(правильный выбор 1-го числа)• P(правильный выбор 2-го числа)• P(правильный выбор 5-го числа)=(110)•(110)•(110) •(110)•(110)=0,00001

Следовательно, вероятность выигрыша равна 0,00001, а вероятность проигрыша равна 1 − 0,00001 = 0,99999. Вот так мы получаем третий столбец P ( x ) в таблице PDF ниже.

Чтобы получить четвертый столбец x P ( x ) в таблице, мы просто умножаем значение x на соответствующую вероятность P ( x ).

Таблица PDF выглядит следующим образом:

	х	Р ( х )	х * Р ( х )
Потеря	–2	.99999	(–2)(0,99999) = –1,99998
Прибыль	100 000	. 00001	(100 000)(.00001) = 1

Таблица 4.9

Затем мы суммируем все продукты в последнем столбце, чтобы получить среднее/ожидаемое значение X

 E(X)=µ=∑xP(x)=−1,99998+1=-0,9998. E(X)=μ=∑xP(x)=−1,99998+1=−0,9998.

Поскольку –0,99998 равно –1, в среднем вы ожидаете, что будете терять примерно 1 доллар за каждую игру, в которую вы играете. Однако каждый раз, когда вы играете, вы либо теряете 2 доллара, либо получаете 100 000 долларов. 1 доллар — это средний или ожидаемый проигрыш за игру после многократного прохождения этой игры.

Пример 4.6

Предположим, вы играете в игру со смещенной монетой. Вы играете в каждую игру, подбрасывая монету один раз. P (головки) = 2323 и P (решка) = 1313. Если выпадет решка, вы заплатите 6 долларов. Если вы подбросите решку, вы выиграете 10 долларов. Если вы будете играть в эту игру много раз, выйдете ли вы вперед?

а. Задайте случайную величину X .

Раствор 4.6

а. Х = сумма прибыли

б. Заполните следующую таблицу ожидаемых значений:

	х	____	____
ВИН	10	1313	____
ПОТЕРЯ	____	____	–123–123

Таблица 4.10

Решение 4.6

b.

	х	Р ( х )	xP ( x )
ВЫИГРЫШ	10	1313	103103
ПОТЕРЯ	–6	2323	–123–123

Таблица 4. 11

 

 

c. Каково ожидаемое значение, μ ? Ты выходишь вперед?

Раствор 4.6

c. Добавьте последний столбец таблицы. Ожидаемое значение   E(X)=μ=103+(−123)=−23≈−0,67(X)=μ=103+(−123)=−23≈−0,67. Вы теряете в среднем около 67 центов каждый раз, когда играете в игру, так что вы не выходите вперед.

Обычно для вероятностных распределений мы используем калькулятор или компьютер для расчета μ и σ , чтобы уменьшить ошибки округления. Для некоторых распределений вероятностей существуют сокращенные формулы для вычисления μ и σ .

Пример 4.7

Дважды подбросьте правильный шестигранный кубик. Пусть X = количество граней, которые показывают четное число. Составьте таблицу, подобную таблице 4.12, и рассчитайте среднее значение μ и стандартное отклонение 9. 0057 σ из X .

Решение 4.7

Подбрасывание одного правильного шестигранного кубика дважды занимает такое же пространство выборки, как и подбрасывание двух правильных шестигранных игральных костей. Выборочное пространство имеет 36 результатов.

The final row contains the following ordered pairs: 6 and 1, 6 and 2, 6 and 3, 6 and 4, 6 and 5, and 6 and 6.»>

(1, 1)	(1, 2)	(1, 3)	(1, 4)	(1, 5)	(1, 6)
(2, 1)	(2, 2)	(2, 3)	(2, 4)	(2, 5)	(2, 6)
(3, 1)	(3, 2)	(3, 3)	(3, 4)	(3, 5)	(3, 6)
(4, 1)	(4, 2)	(4, 3)	(4, 4)	(4, 5)	(4, 6)
(5, 1)	(5, 2)	(5, 3)	(5, 4)	(5, 5)	(5, 6)
(6, 1)	(6, 2)	(6, 3)	(6, 4)	(6, 5)	(6, 6)

Таблица 4.13

Используйте свободное место для заполнения следующей таблицы:

The header row contains the following column titles: x, p opening parenthesis x closing parenthesis, x p opening parenthesis x closing parenthesis, and opening parenthesis x minus mu closing parenthesis superscript 2 times p opening parenthesis x closing parenthesis. The first data row contains 0, nine thirty-sixths, 0, and opening parenthesis 0 minus 1 closing parenthesis superscript 2 times nine thirty-sixths equals nine thirty-sixths. The second data row contains 1, eighteen thirty-sixths, eighteen thirty-sixths, and opening parenthesis 1 minus 1 closing parenthesis superscript 2 times eighteen thirty-sixths equals 0. The final row contains 2, nine thirty-sixths, eighteen thirty sixths, and opening parenthesis 1 minus 1 closing parenthesis superscript 2 times nine thirty-sixths equals nine thirty-sixths.»>

Расчет μ и σ .

х	Р ( х )	х Р ( х )	( x – μ ) 2 ⋅⋅ P ( x )
0	936936	0	(0 – 1) 2 ⋅ 936936 = 936936
1	18361836	18361836	(1 – 1) 2 ⋅ 18361836 = 0
2	936936	18361836	(2 – 1) 2 ⋅ 936936 = 936936

Таблица 4. 14

Сложите значения в третьем столбце, чтобы найти ожидаемое значение: μ = 36363636 = 1. Используйте это значение, чтобы заполнить четвертый столбец.

Сложите значения в четвертом столбце и извлеките квадратный корень из суммы: σ = 18361836 ≈ 0,7071.

Некоторые из наиболее распространенных дискретных функций вероятности — биномиальная, геометрическая, гипергеометрическая и функция Пуассона. Большинство элементарных курсов не охватывают геометрические, гипергеометрические и пуассоновские. Ваш инструктор сообщит вам, если он или она желает покрыть эти раздачи.

Функция распределения вероятностей является образцом. Вы пытаетесь подогнать вероятностную задачу под шаблон или распределение, чтобы выполнить необходимые вычисления. Эти распределения являются инструментами, облегчающими решение вероятностных задач. Каждый дистрибутив имеет свои особенности. Изучение характеристик позволяет различать разные дистрибутивы.