Дана плотность распределения случайной величины найти параметр а: Пример расчета математического ожидания непрерывной случайной величины

Пример расчета математического ожидания непрерывной случайной величины

Чтобы найти функцию распределения дискретной случайной величины, необходимо использовать данный калькулятор.

Задание 1. Плотность распределения непрерывной случайной величины Х имеет вид:
Найти:
а) параметр A;
б) функцию распределения F(x);
в) вероятность попадания случайной величины X в интервал [1;2];
г) математическое ожидание MX и дисперсию DX.
Построить график функций f(x) и F(x).

Решение.

Скачать решение

Задание 2. Найти дисперсию случайной величины X, заданной интегральной функцией.

Задание 3. Найти математическое ожидание случайной величины Х заданной функцией распределения.

Перейти к онлайн решению своей задачи

Задание 4.

Плотность вероятности некоторой случайной величины задана следующим образом: f(x) = A/x⁴ (x = 1; +∞)
Найти коэффициент A, функцию распределения F(x), математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [0,2]. Построить графики f(x) и F(x).

Задача. Функция распределения некоторой непрерывной случайной величины задана следующим образом:

Определить параметры a и b, найти выражение для плотности вероятности f(x), математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [2,3]. Построить графики f(x) и F(x).

• Решение
• Видео решение

Найдем функцию плотности распределения, как производную от функции распределения.

F′=f(x)=a
Зная, что найдем параметр a:

или 3a=1, откуда a = 1/3
Параметр b найдем из следующих свойств:
F(4) = a*4 + b = 1
1/3*4 + b = 1 откуда b = -1/3
Следовательно, функция распределения имеет вид: F(x) = (x-1)/3

Математическое ожидание.


Дисперсия.

¹/₉•4³ — (¹/₉•1³) — (⁵/₂)² = ³/₄
Найдем вероятность того, что случайная величина примет значение в интервале [2,3]
P(2 < x< 3) = F(3) – F(2) = (1/3*3 — 1/3) — (1/3*2 — 1/3) = 1/3

Пример №1. Задана плотность распределения вероятностей f(x) непрерывной случайной величины X. Требуется:

1. Определить коэффициент A.
2. найти функцию распределения F(x).
3. схематично построить графики F(x) и f(x).
4. найти математическое ожидание и дисперсию X.
5. найти вероятность того, что X примет значение из интервала (2;3).

f(x) = A*sqrt(x), 1 ≤ x ≤ 4.
Решение:

Случайная величина Х задана плотностью распределения f(x):

Найдем параметр A из условия:



или
14/3*A-1 = 0
Откуда,
A = ³/₁₄
Функцию распределения можно найти по формуле.


Математическое ожидание находится по следующей формуле:


Дисперсия выражена формулой:

³/₄₉•4^7/₂ — (³/₄₉ •1^7/₂) — (⁹³/₃₅)² = ⁸⁷⁶/₁₂₂₅
Вероятность того, что X примет значение из интервала (2;3):

Скачать пример №1

Пример №2. Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).

Плотность распределения вероятностей — f(x)

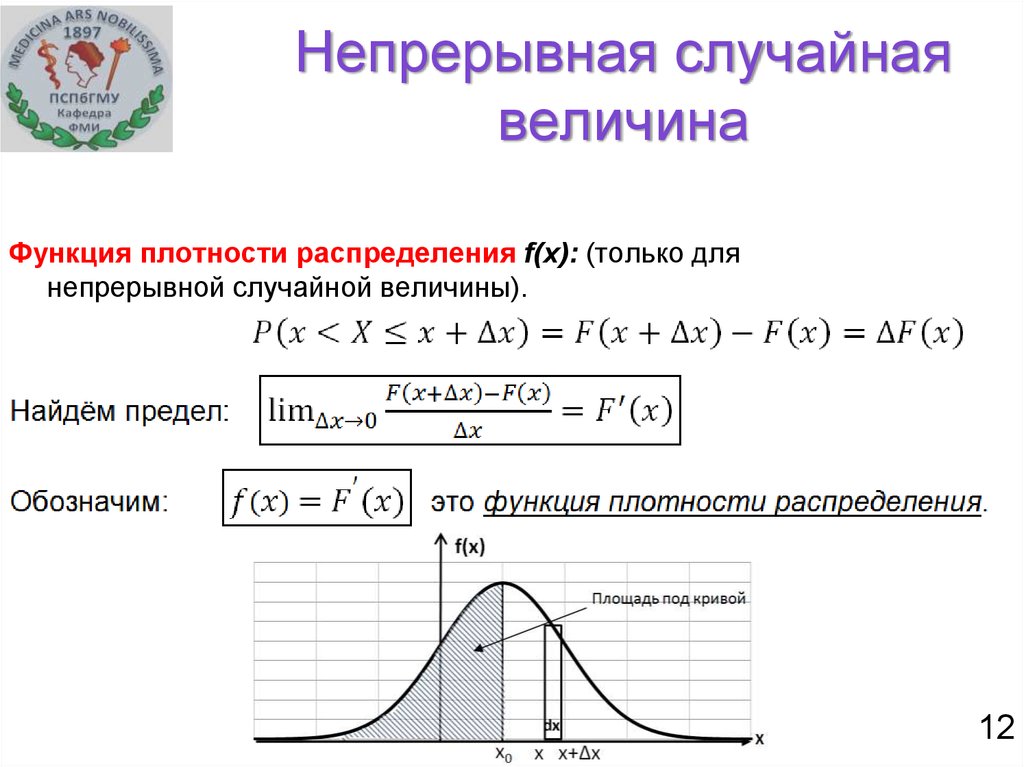
Для непрерывных случайных величин наряду с законом распределения вероятностей рассматривают плотность вероятностей, которую обозначают так .

Плотностью вероятностей случайной величины называют первую производную от интегральной функции распределения вероятностей

откуда дифференциал

Поскольку прирост определяют зависимости

куплена плотности вероятностей на прирост случайной величины соответствует вероятность того, что случайная величина содержаться в промежутке где .

Геометрически на графике плотности вероятностей соответствует площадь прямоугольника с основанием и высотой

Свойства плотности вероятностей

1. Плотность вероятностей принимает положительные значения . Это свойство следует из определения первой производной от функции распределения , которая в свою очередь является неубывающей функцией.

2. Условие нормирования случайной величины

3.Вероятность попадания случайной величины в промежуток определяется зависимостью

4. Функция распределения вероятностей непрерывной случайной величины определяется через плотность распределения вероятностей интегрированием

—————————————

Рассмотрим задачи для закрепления материала на практике.

Пример 1. Закон распределения случайной величины заданы функцией

Найти плотность распределения вероятностей и построить графики обеих функций . Вычислить вероятность того, что случайная величина принадлежит промежутку

Решение.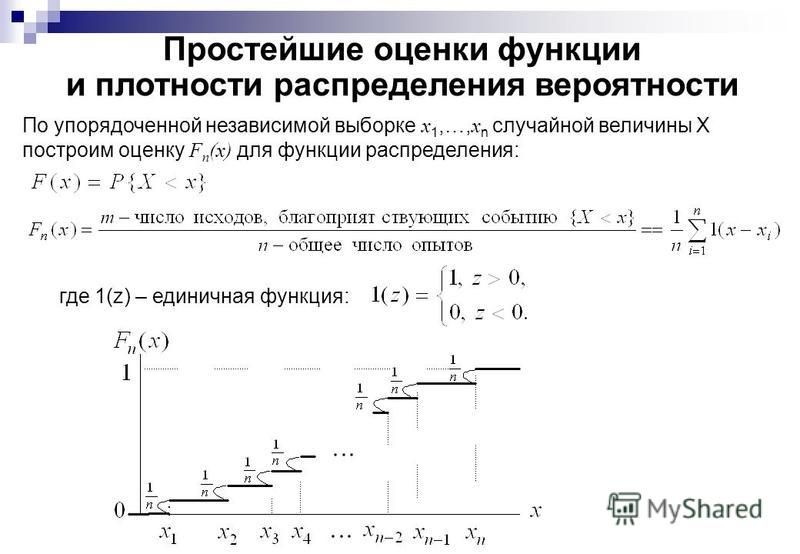 Вычисляем функцию плотности вероятностей

Графики функций изображены на рисунках

 

 

Вероятность события вычислим по формуле

Согласно приведенной выше формулы получим

На этом задача решена.

———————————————

Пример 2. По заданной функцией плотности распределения вероятностей

установить параметры и функцию распределения вероятностей . Построить графики функций.

Решение. Значение постоянной определяем из условия нормировки

При найденном значении плотность вероятностей будет иметь вид

Функция распределения вероятностей определяется интегрированием:

Записываем общий вид функции ,

Графики функций распределения вероятностей и ее плотности показаны на рисунках ниже

 

 

 

—————————————

Пример 3. Случайная величина имеет закон распределения вероятностей в виде треугольника

Записать выражения для плотности вероятностей и функции распределения вероятностей, построить график и вычислить .

Решение. На промежутках и плотность вероятностей меняется по линейному закону вида

для первого и второго участки соответственно. Для нахождения неизвестных констант установим ординаты вершины треугольника . Используем условие нормирования, согласно которому площадь треугольника равна единице:

При известных координатах всех вершин находим уравнение прямых

Есть другой способ нахождения уравнения прямых, предусматривающий отыскания по одной константе на уравнение. Если известна точка пересечения прямой с осью ординат , то уравнение прямой которая через эту точку проходит следующее

где – ордината пересечения с осью . Подстановкой второй точки прямой находят неизвестную константу . Для заданных точек получим

Со временем второй метод для Вас станет проще и практичнее в использовании. Плотность вероятностей примет значение

а ее функция примет вид

Функцию распределения вероятностей находим интегрированием:

а) на промежутке :

2) на промежутке

Следовательно, функция распределения вероятностей такая

Ее график приведен ниже

Вычисляем вероятность события согласно формуле

или

Следовательно, вероятность равна

————————-

Хорошо проанализируйте приведенные примеры — это поможет научиться быстро находить плотность распределения вероятностей и выполнять построение графика. Будьте внимательны при интегрировании и выбирайте удобную для вычислений методику.

Вероятность

— найти CDF, дисперсию и найти параметр для заданной плотности.

Задавать вопрос

спросил 4 года 9 месяцев назад

Изменено 4 года, 9 месяцев назад

Просмотрено 33 раза

$\begingroup$ 9{12}$

$(C)$ ?

Итак, моя просьба к этому сообщению: пожалуйста, проверьте приведенные выше расчеты и формулы, в частности, и пришлите мне любые советы в соответствии с $(C)$, потому что я понятия не имею, как это сделать. Любая помощь будет оценена.

• вероятность
• теория вероятностей

$\endgroup$

$\begingroup$

$c$ характеризуется следующим уравнением, которое должно выполняться для PDF:

$$\int_{-\infty}^{\infty}cx^4\mathbf{1}_{[0,6]} \ дх = с \ int_0 ^ 6x ^ 4 \ дх = 1. $ $ 94}$ подтверждено.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Распределения функций случайных величин

Пусть \(X_i\) обозначает, одобряет ли случайно выбранный человек работу президента. Более конкретно:

• Пусть \(X_i=1\), если человек одобряет работу президента, с вероятностью \(p\)
• Пусть \(X_i=0\), если человек не одобряет работу президента с вероятностью \(1-p\)

Затем вспомним, что \(X_i\) — случайная величина Бернулли со средним значением: 92=np(1-p)\)

Теперь пусть \(n=10\) и \(p=\frac{1}{2}\), так что \(Y\) является биномиальным(\( 10, \frac{1}{2}\)). Какова вероятность того, что ровно пять человек одобряют работу президента?

Решение

Здесь нет ничего нового. Мы можем рассчитать точную вероятность, используя биномиальную таблицу в конце книги с \(n=10\) и \(p=\frac{1}{2}\). Таким образом, мы получаем:

\begin{align} P(Y=5)&= P(Y \leq 5)-P(Y \leq 4)\\ &= 0,6230-0,3770\\ &= 0,2460\\ \end{выравнивание}

То есть с вероятностью 24,6% ровно пять человек из десяти выбранных одобряют работу президента.

Обратите внимание, однако, что \(Y\) в приведенном выше примере определяется как сумма независимых, одинаково распределенных случайных величин. Следовательно, пока \(n\) достаточно велико, мы можем использовать центральную предельную теорему для вычисления вероятностей для \(Y\). В частности, Центральная предельная теорема говорит нам, что:

\(Z=\dfrac{Y-np}{\sqrt{np(1-p)}}\stackrel {d}{\longrightarrow} N(0,1) \). 92=np(1-p)=10\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right)=2.5\)

Теперь, если мы посмотрим на график биномиального распределения с прямоугольником, соответствующим \(Y=5\), заштрихованным красным: нам было бы полезно внести некоторую поправку на тот факт, что мы используем непрерывное распределение для аппроксимации дискретного распределения. В частности, кажется, что прямоугольник \(Y=5\) действительно включает все \(Y\) больше 4,5, но меньше 5,5. То есть:

\(P(Y=5)=P(4.5< Y < 5.5)\)

Такая корректировка называется « коррекция непрерывности «. После того, как мы сделали поправку на непрерывность, вычисление сводится к обычному вычислению вероятности:

Теперь вспомните, что ранее мы использовали биномиальное распределение, чтобы определить, что вероятность того, что \(Y=5\), точно равна 0,246. Здесь мы использовали нормальное распределение, чтобы определить, что вероятность \(Y=5\) приблизительно равна 0,251. Это неплохое приближение, учитывая тот факт, что мы имеем дело с относительно небольшим размером выборки \(n=10\)!

Попробуем еще несколько приближений. Какова вероятность того, что более 7, но не более 9 человек из десяти опрошенных одобряют работу президента?

Решение

Если мы посмотрим на график биномиального распределения с площадью, соответствующей \(7 581N — 1000

мы должны увидеть, что мы хотим сделать следующую поправку на непрерывность:

\(P(7

Теперь снова, когда мы сделали поправку на непрерывность, расчет сводится к обычному расчету вероятности:

Кстати, вам может быть интересно отметить, что приблизительная нормальная вероятность весьма близка к точной биномиальной вероятности. Мы показали, что приблизительная вероятность равна 0,0549, тогда как следующий расчет показывает, что точная вероятность (с использованием биномиальной таблицы с \(n=10\) и \(p=\frac{1}{2}\) равна 0,0537:

\(P(7

Попробуем еще одно приближение. Какова вероятность того, что по крайней мере 2, но менее 4 из десяти опрошенных одобряют работу президента?

Решение

Если мы посмотрим на график биномиального распределения с площадью, соответствующей \(2\le Y<4\), заштрихованной красным цветом: - 5StDev - 1. 581N — 1000

мы должны увидеть, что мы хотим сделать следующую поправку на непрерывность:

\(P(2 \leq Y <4)=P(1.5< Y < 3.5)\)

Опять же, как только мы сделали коррекция непрерывности, расчет сводится к обычному расчету вероятности:

\begin{align} P(2 \leq Y <4)=P(1.5< Y <3.5) &= P(\dfrac{1.5-5}{\ sqrt{2,5}}0,95)-P( Z>2,21)\\ &= 0,1711-0,0136=0,1575\\ \end{выравнивание}

Между прочим, точная биномиальная вероятность равна 0,1612, как показывает следующий расчет:

\(P(2 \leq Y <4)=P(Y\leq 3)-P(Y\leq 1)=0,1719 -0,0107=0,1612\)

Всего пара комментариев, прежде чем мы закончим обсуждение нормального приближения к двучлену.

(1) Во-первых, мы еще не обсуждали, что означает «достаточно большой» с точки зрения того, когда уместно использовать нормальное приближение к двучлену. Общее эмпирическое правило состоит в том, что размер выборки \(n\) является «достаточно большим», если:

\(np\ge 5\) и \(n(1-p)\ge 5\)

Например, в приведенном выше примере, в котором \(p=0,5\), два условия выполнено, если:

\(np=n(0,5)\ge 5\) и \(n(1-p)=n(0,5)\ge 5\)

Теперь оба условия верны, если:

\(n\ge 5\left(\frac{10}{5}\right)=10\)

Поскольку размер нашей выборки был не менее 10 (ну, едва ли!), мы теперь понимаем, почему наши приближения были довольно близко к точным вероятностям. Как правило, чем дальше \(p\) от 0,5, тем больше требуется размер выборки \(n\). Например, предположим \(p=0,1\). Тогда два условия выполняются, если:

\(np=n(0.1)\ge 5\) и \(n(1-p)=n(0.9)\ge 5\)

Теперь первое условие выполнено, если:

\ (n\ge 5(10)=50\)

Второе условие выполняется, если:

\(n\ge 5\left(\frac{10}{9}\right)=5.5\)

То есть оба условия выполняются только если \(n\ge 50\). Таким образом, при \(p=0,5\) достаточно размера выборки \(n=10\). Но если \(p=0,1\), то нам нужен гораздо больший размер выборки, а именно \(n=50\).

(2) По правде говоря, если у вас есть доступные инструменты, такие как биномиальная таблица или статистический пакет, вы, вероятно, захотите вычислить точные вероятности, а не приблизительные вероятности. Значит ли это, что вся наша дискуссия здесь напрасна? Нет, вовсе нет! На самом деле мы чаще всего будем использовать центральную предельную теорему применительно к сумме независимых случайных величин Бернулли, чтобы помочь нам сделать выводы об истинной пропорции населения \(p\).