Что такое действительное число? Ответ на webmath.ru
Содержание:
- Определение действительного числа
- Сложение действительных чисел
- Вычитание действительных чисел
- Умножение действительных чисел
- Деление действительных чисел
- Свойства операции сложения действительных чисел
- Свойства операции умножения действительных чисел
Определение действительного числа
Определение
Действительными или вещественными числами называются все положительные числа, отрицательные числа и нуль.
Множество действительных чисел объединяет в себе множество рациональных и иррациональных чисел. Обозначается множество действительных чисел $R$ .
Например. $\frac{2}{3} ; 0,754 ;-23 ;-\frac{5}{4} ; 113 ;-\sqrt[3]{2} ;-2,34 ; \frac{1}{\pi}$ — все это действительные числа.
На множестве действительных чисел можно ввести четыре арифметические операции:
сложение,
вычитание,
умножение и
деление.
Сложение действительных чисел
Для любых двух действительных чисел $a$ и $b$ существует единственное число $c$, называемое суммой этих чисел. При этом
Свойства операции сложения действительных чисел
Коммутативный закон сложения: для любой пары чисел $a$ и $b$
$$a+b=b+a$$
Ассоциативный закон сложения: для любой тройки чисел $a$, $b$ и $c$
$$(a+b)+c=a+(b+c)$$
Нейтральный элемент: существует число, обозначаемое 0 и называемое нулем, такое, что для любого числа $a$
$$a+0=0+a=a$$
Для любого числа $a$ существует число, обозначаемое $(-a)$, такое, что
$$a+(-a)=(-a)+a=0$$
число $(-a)$ называется противоположным числу $a$ ;
Вычитание действительных чисел
Для любых двух действительных чисел $a$ и $b$ число $c=a+(-b)$ называется разностью чисел $a$ и $b$, и обозначается
Пример
Задание.
Найти сумму и разность действительных чисел $23$ и $12,4$
Решение. Сумма заданных чисел равна $23+12,4=35,4$
Разность: $23-12,4=10,6$
Ответ.
$23+12,4=35,4$
$23-12,4=10,6$
Умножение действительных чисел
На множестве действительных чисел определена операция называемая умножением. Для любых двух действительных чисел $a$ и $b$ существует единственное число $c$, называемое их произведением и обозначаемая
Свойства операции умножения действительных чисел
Коммутативный закон сложения: для любой пары чисел $a$ и $b$
$$a \cdot b=b \cdot a$$
Ассоциативный закон умножения: для любой тройки чисел $a$, $b$ и $c$
$$(a \cdot b) \cdot c=a \cdot(b \cdot c)$$
Нейтральный элемент: существует число, обозначаемое символом 1 и называемое единицей, такое, что для любого числа $a$
$$a \cdot 1=1 \cdot a$$
Для любого числа $a$, отличного от нуля, существует число, обозначаемое $$(1 / a)$$, такое, что
$$a \cdot \frac{1}{a}=\frac{1}{a} \cdot a=1$$
число $$(1 / a)$$ называется обратным числу $a$ ;
Деление действительных чисел
Для любых двух действительных чисел $a$ и $b$ ( $b$ отлично от нуля) существует число $c$
$$c=a \cdot \frac{1}{b}$$
называется частным от деления числа $a$ на $b$, и обозначается
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание.
Решение. Произведение заданных чисел равно $1,2 \cdot 5=6$
Частное: $1,2 : 5=1,2 \cdot \frac{1}{5}=1,2 \cdot 0,2=0,24$
Ответ.
$1,2 \cdot 5=6$
$1,2 : 5=0,24$
Операции сложения и умножения действительных чисел связаны законом дистрибутивности умножения относительно сложения:
$$(a+b) \cdot c=a \cdot c+b \cdot c$$
Читать дальше: что такое четное число.
Действительные числа – примеры, определение, символ (6 класс, математика)
4.3
Средняя оценка: 4.3
Всего получено оценок: 362.
4.3
Средняя оценка: 4.3
Всего получено оценок: 362.
Действительные числа – это очень большой блок значений. Фактически любое число, которое встречается вам в школьном курсе можно считать действительным. Но нужно уметь различать, к какому множеству относится заданное число, ведь существуют разные виды действительных чисел – об этом и пойдет речь сегодня.
Множества чисел
Зачем вообще нужно определение разных множеств чисел? Ведь было бы куда проще просто взять число и начать выполнять какие-либо действия. Но все не так просто.
Вы наверняка уже сталкивались со сложностью вычисления дробей? Сложение, умножение, деление и вычитания – все действия с дробями отличаются от действий с привычными нам натуральными числами, ведь они относятся другому подмножеству.
То же касается, к примеру, отрицательных чисел. Складывать их с положительными можно, но только по отдельным правилам. Поэтому в вопросе множеств чисел нужно разбираться с самого начала.
Все существующие числа можно разделить на действительные и комплексные. Комплексные числа в школьном курсе не изучаются. В этом подмножестве можно извлечь корень из -1, это единственное, что в 6 классе нужно знать о комплексных числах. А знать это нужно, чтобы понимать: если у уравнения нет решений, то, скорее всего, его нет только среди действительных чисел. А вот среди комплексных это решение может и найтись.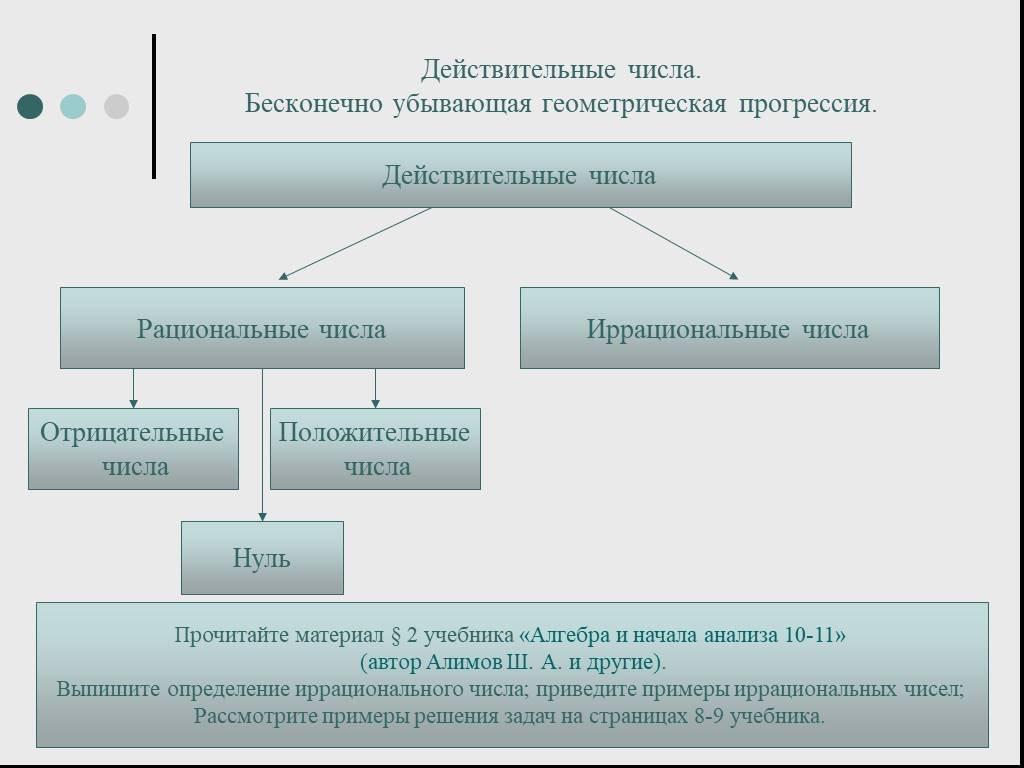
Действительным числами зовутся любые:
- Положительные числа: целые и дробные.
- Отрицательные числа: целые и дробные.
- Число ноль.
Это именно те числа, которые мы используем для наиболее распространенных математических действий. Примеры действительных чисел: 5; 5,13; $\sqrt{13}$.
Эти числа обозначаются общим символом R.Иррациональные числа так же входят в сообщество действительных чисел.
Подмножества чисел
Действительные числа состоят из подмножеств, каждое из которых следует рассмотреть отдельно:
- Натуральные числа. Натуральные числа были так названы еще древними греками. Натуральные или природные – это первые числа, которые придумало человечество. Их до сих пор используют для счета на рынке или в магазине. Там, где не нужны сложные и долгие вычисления: для простого счета используется именно эта категория чисел.
- Целые числа. Сюда входят помимо натуральных, еще и число ноль и отрицательные числа, но только целые.
Дроби в эту категорию не входят. - Рациональные числа. Сюда входят все целые и натуральные числа, а так же любые дроби.
- Иррациональные числа. Это подмножество не пересекается с рациональными числами, но так же относится к действительным числам.
Дроби в эту категорию не входят.Обратите внимание, что число 0 для счета не используется, то есть оно не относится к натуральным числам. Само число 0 было изобретено гораздо позднее натуральных чисел, в Индии. Это открытие считается одним из величайших событий в математике.
Также нельзя забывать, что рациональные и иррациональные числа хоть и относятся к действительным, но подчиняются разным правилам счета. Это нужно учитывать при решении уравнений и примеров.
Что мы узнали?
Мы поговорили о множествах чисел. Выяснили, что числа делятся на действительные числа и комплексные числа. Действительные числа в свою очередь подразделяются на рациональные и иррациональные. Мы поговорили о разнице в действиях с рациональными и иррациональными числами.
Проговорили все подмножества иррациональных чисел.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Назар Шевченко
10/10
Виктория Матяшова
9/10
Шахтёрский Увк
8/10
Надежда Мальцева
8/10
Оценка статьи
4.3
Средняя оценка: 4.3
Всего получено оценок: 362.
А какая ваша оценка?
Могут ли действительные числа быть отрицательными?
Алгебра
Наука
- Анатомия и физиология
- астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
- Преалгебра
- Предварительный расчет
- Статистика
- Тригонометрия
Гуманитарные науки
- Английская грамматика
- История США
- Всемирная история
- Сократическая мета
- Избранные ответы
.
.. и не толькоТемы
Влияние этого вопроса
5339 просмотров по всему миру
Вы можете повторно использовать этот ответ
Лицензия Creative Commons
Начальный курс алгебры 5
Начальный курс алгебры
Курс 5. Сложение вещественных чисел бюстгальтер
Цели обучения
После завершения этого руководства вы сможете:
- Сложите действительные числа с одинаковым знаком.
- Сложите действительные числа с разными знаками.
- Найдите добавку, обратную или противоположную числу.
Введение
В этом руководстве рассматривается добавление действительных чисел, а также найти добавку обратное или противоположное числу. У меня есть все возможное уверенность что вы знакомы с дополнением , но иногда норм для отрицательные числа (фу!) время от времени немного путаются. Таким образом, хорошо просмотреть их, чтобы убедиться, что они у вас есть.
Учебник
Добавление реальных чисел
Добавление действительных чисел
с одинаковым знаком
Шаг 1: Добавьте
абсолютные значения.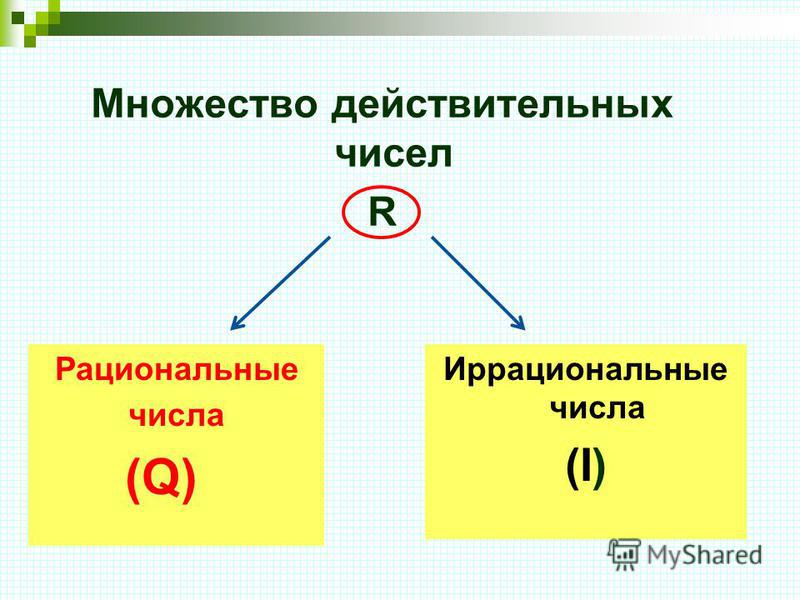
Если вам нужен обзор абсолютные значения, перейдите к Уроку 2: Символы и наборы чисел.
Шаг 2: Прикрепить
их общий признак
подвести.
Другими словами:
Если оба добавляемых числа положительные, тогда у вас будет положительный ответ.
Если оба добавляемых числа отрицательные тогда у вас будет отрицательный ответ.
Пример 1: Добавьте -6 + (-8).
-6 + (-8) = -14
Сумма абсолютных значений будет равна 14, а их
общий признак
-.
Вот как мы получаем ответ -14.
Вы также можете представить это как деньги. Я знаю, что мы все можем относиться к этому. Подумайте о отрицательный как убыток. В этом примере вы можете думать об этом как о потере 6 долларов, а затем потеряв еще 8 долларов за полная потеря 14 долларов.
Пример 2: Добавить -5,5 + (-8,7).
-5,5 + (-8,7) = -14,2
Сумма абсолютных значений будет равна 14,2, а их общий признак -. Так мы получаем ответ -14.2.
Вы также можете представить это как
деньги — я знаю
мы все можем относиться к этому.
Думайте о негативе как о
потеря. В этом примере вы можете думать об этом как о потере 5,5
долларов
а затем потеряв еще 8,7 доллара на общих убытка в 14,2
долларов.
Добавление действительных чисел
с противоположными знаками
Шаг 1: Возьмите
разница в абсолюте
ценности.
Если вам нужен обзор абсолютные значения, перейдите к Уроку 2: Символы и наборы чисел.
Шаг 2: Прикрепите
знак числа
которая имеет более высокое абсолютное значение.
Чего у вас было больше, отрицательного или отрицательного? положительный?
Если число с большим абсолютным значением
отрицательный, то ваш
сумма отрицательная.
Другими словами, у вас больше негатива, чем
положительный.
Если число с большим абсолютным значением было положительный, то ваш сумма положительная. Другими словами, у вас больше позитива, чем у отрицательный.
Пример 3: Добавить -8 + 6.
-8 + 6 = -2.
Разница между 8 и 6 равна 2 и знаку 8 (больший абсолютный значение) равно -. Так мы получаем ответ -2.
Думая о деньгах: мы потерянный 8 долларов и вернули 6 долларов, так что мы все еще в яме 2 долларов.
Пример
4: Добавить .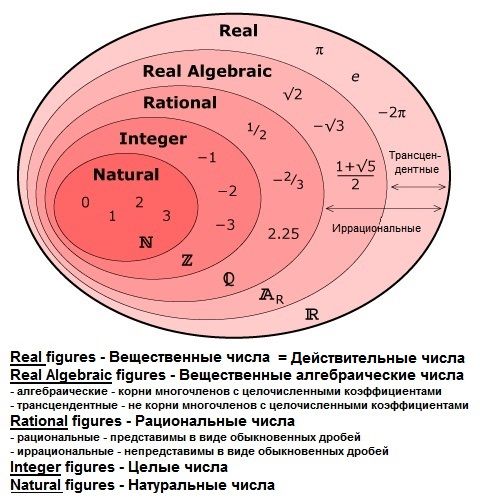
*Множ. верх и низ первого
дробь на 2, чтобы получить LCD 6
*Возьмите разницу числители и записать над общим знаменателем 6
*Уменьшить дробь
Разница между 4/6 и 1/6 составляет 3/6 = 1/2, а знак 4/6 (большее абсолютное значение) равно +. Так мы получаем отвечать 1/2.
Думая о деньгах: мы имел 2/3 доллара и потеряли 1/6 доллара, поэтому мы вышли вперед 1/2 доллара.
Обратите внимание: если вам нужна помощь по дробям, вернитесь к Учебнику. 3: дроби.
Пример
5: Добавить -10 + 7 + (-2) + 5.
В этом примере нам нужно объединить более два числа вместе, но мы по-прежнему будем следовать тому же мыслительному процессу, который мы делаем, если есть только два числа. Я собираюсь пойти дальше и пройти через это, двигаясь налево к верно.
* -10 + 7 = -3
* -3 + (-2) = -5
Пример 6: Добавить .
В этой задаче на сложение у нас есть несколько абсолютных значений
бросили в
микс. Помните, что нам нужно делать то, что находится внутри абсолютного
значения (символ группировки), а затем сложить эти числа вместе.
Если
вам нужно обзор по заказу
операции перейдите к Учебнику 4: Знакомство с переменными выражениями и
Уравнения.
*Добавить абсолютные значения
*Вычислить абсолютные значения
*Добавить
Противоположности
Противоположности — это два числа, которые находятся на противоположных сторонах происхождения (0) на числовой прямой, но имеют одинаковое абсолютное значение. Другими словами, противоположности находятся на одинаковом расстоянии от начала координат, но в противоположных направлениях.
Противоположностью x является номер — х .
Имейте в виду, что противоположность 0 равна 0.
Ниже приведена иллюстрация противоположностей с использованием
цифры 3
и -3:
Двойное отрицательное свойство
Для каждого действительного числа a ,
-(- a ) = a .
Если вы видите знак минус перед выражением,
ты можешь думать
из него как принимать противоположное ему. Например, если у вас было
-(-2),
вы можете думать об этом как о противоположности -2. Поскольку число может
только
иметь один из двух знаков, либо «+», либо «-», то противоположность
отрицательный
должен быть положительным. Итак, -(-2) = 2,
Пример
7: Напишите добавку, обратную или противоположную
1.
5.
Противоположное 1,5 равно -1,5 , так как оба эти числа имеют одинаковое абсолютное значение, но находятся по разные стороны от начала координат на числовая строка.
Пример 8: Запишите значение, противоположное -3.
Противоположностью -3 является 3 , так как оба эти числа имеют одинаковое абсолютное значение, но находятся по разные стороны от начала координат на число линия.
Пример 9: Упростить -(-10).
Если перед скобкой стоит отрицание, например
это, это
другой способ написать, что вам нужно найти добавку, обратную или
противоположный.
Поскольку отрицательным является положительный, наш ответ 10.
Пример 10: Упростить -|-5,2|.
-|-5.2| =
-(5.2) =
-5.2
*Вычислить абсолютное значение
*Найти противоположное
Практические задачи
Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
виды проблем. Математика работает так же, как
что-либо
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
это.
Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этих вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1а — 1г: Доп.
1а. -15 + 7
(ответ/обсуждение
к 1а)
1б.
(ответ/обсуждение
к 1b)
1c. 3,2 + (-1,3) + (- 4,1)
(ответ/обсуждение
к 1с)
1д. |- 4 + (-3) + 2|
(ответ/обсуждение
к 1д)
Практика Задачи 2a — 2b: Найдите обратную или противоположную добавку.
2а. ½
(ответ/обсуждение
к 2а)
2б. -20
(ответ/обсуждение
к 2б)
Практика Задачи 3a — 3b: Упростить.
3а. -(- 4)
(ответ/обсуждение
до 3а)
3б.
(ответ/обсуждение
к 3б)
Нужна дополнительная помощь по этим темам?
Ниже представлена веб-страница
что может помочь
вы в темах, которые были освещены на этой странице:
http://www.mathleague.com/help/integers/integers.htm#addingintegers
На этой веб-странице рассказывается, как складывать целые числа.