Дерево возможных вариантов в комбинаторике: Метод дерева вариантов — Комбинаторные задачи

решение комбинаторных задач, полный граф, граф дерево, примеры

Понятие графа

Кроме таблиц, удобным инструментом для перебора и подсчёта различных комбинаций является граф.

Граф – это абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.

Граф из 6 вершин и 7 ребёр.

Например:

Сколько различных трёхзначных чисел можно написать с помощью цифр 0 и 1?

Получаем 4 числа: 100,101,110 и 111

Полный граф в комбинаторике

Полный граф– это граф со всеми возможными ребрами.

С помощью полного графа удобно решать задачи полного перебора про «всех со всеми».

Например:

5 школьных команд по волейболу сыграли серию игр. Каждая команда провела с другими командами по одному матчу. Сколько всего матчей было сыграно?

Изобразим полный граф с 5-ю вершинами и посчитаем количество ребёр.

N = 10. Значит, было сыграно 10 матчей.

Граф-дерево

Дерево – это граф без циклов, у которого между парами вершин имеется только одно ребро.

Граф-дерево с 9 узлами и 8 ребрами.

Из каждого узла выходит не более 2 ребер.

Такое дерево называют бинарным.

С помощью дерева удобно составлять упорядоченные комбинации элементов.

Например:

На столе стоит три стакана сока – апельсиновый, виноградный и яблочный. Можно взять только два стакана. Сколько есть возможных вариантов и каких?

По правилу произведения число возможных вариантов: $3 \cdot 2 = 6$. Поскольку, порядок выбора неважен, остаётся $\frac{6}{2} = 3$ варианта. Построим граф:

3 варианта: 1) апельсиновый + яблочный, 2)апельсиновый + виноградный, 3) виноградный + яблочный.

Примеры

Пример 1. Вася, Петя, Коля и Толя хотят быть дежурными в столовой. Но можно выбрать только троих. Сколько вариантов выбора есть?

Построим полный граф.

Каждая тройка ребят соответствует треугольнику в этом графе.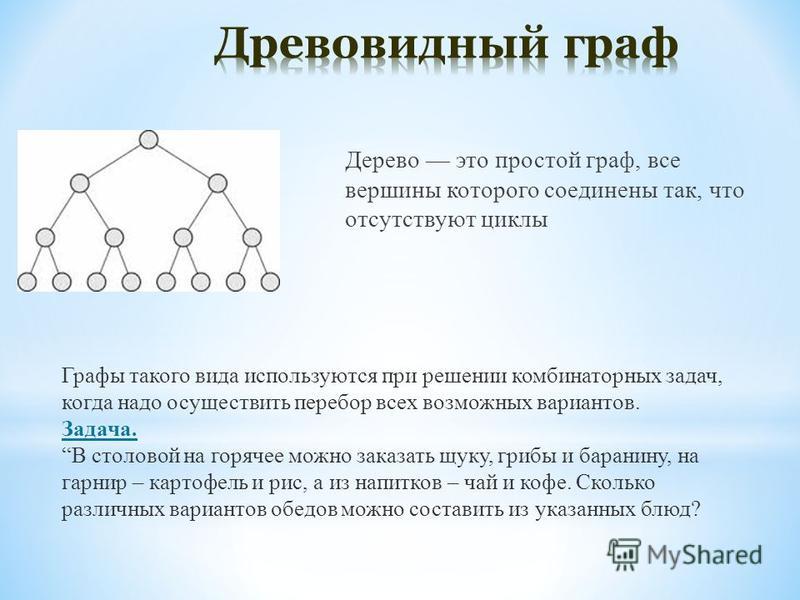

Например, Вася образует три треугольника с оставшимися тремя ребятами:

$ \frac{3\cdot 2}{2} = 3$ — ВПК, ВТК и ВТП

Без Васи есть только один треугольник – ПКТ

Общее количество треугольников 3+1=4

Ответ: 4 варианта

Пример 2. Под рукой есть 6 видов овощей (капуста, морковь, лук, помидоры, огурцы и перец). Для салата нужно 3 вида овощей. Сколько всего различных салатов можно приготовить?

Построим полный граф.

Каждые три овоща на полном графе образуют треугольник.

Например, капуста образует треугольники с оставшимися 5 овощами. Таких треугольников $ \frac{5\cdot 4}{2} = 10$, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).

Количество треугольников, в которые не входит капуста: $ \frac{4\cdot 3}{2} = 6$

Количество треугольников, в которые не входят капуста и морковь: $ \frac{3\cdot 2}{2} = 3$

Количество треугольников, в которые не входят капуста, морковь и перец: $ \frac{2\cdot 1}{2} = 1$

Итого 10+6+3+1 = 20 различных треугольников.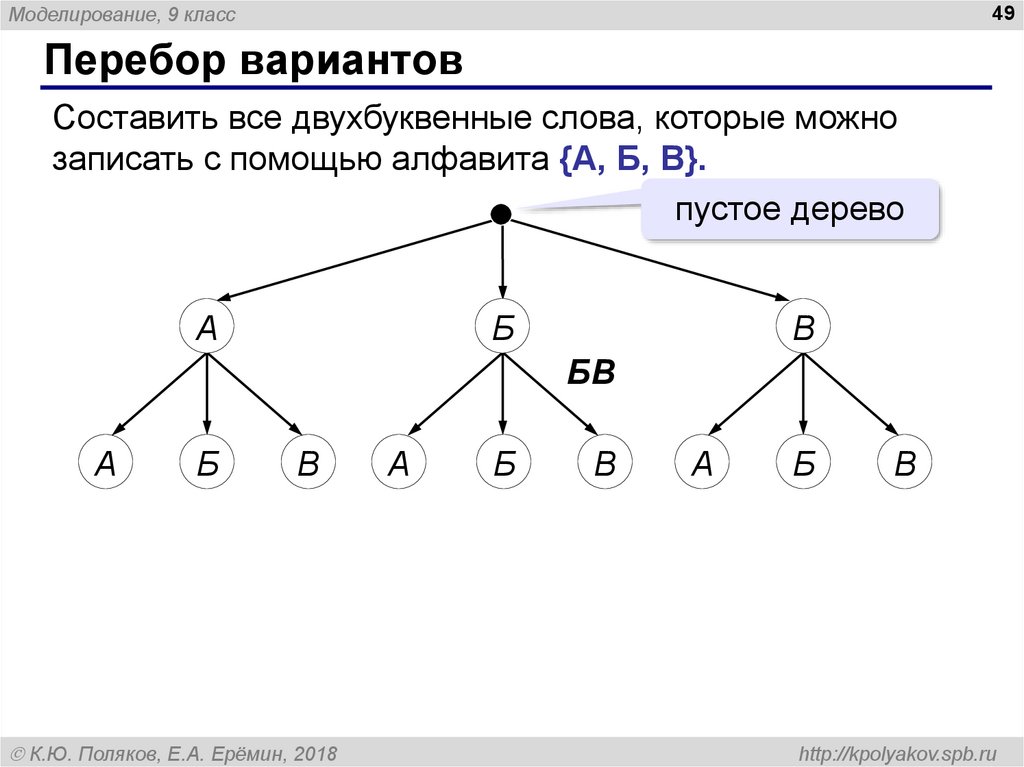

{11} = 11\cdot10\cdot9 = 990 $ — ответ правильный.

Пример 4. В столовой есть на выбор

• два первых блюда: щи (Щ) и борщ (Б)
• три вторых блюда: мясо (М), рыба (Р), блинчики с творогом (Т)
• два напитка: компот (К) и сок (С)

Сколько вариантов обедов можно составить из этих блюд и каких?

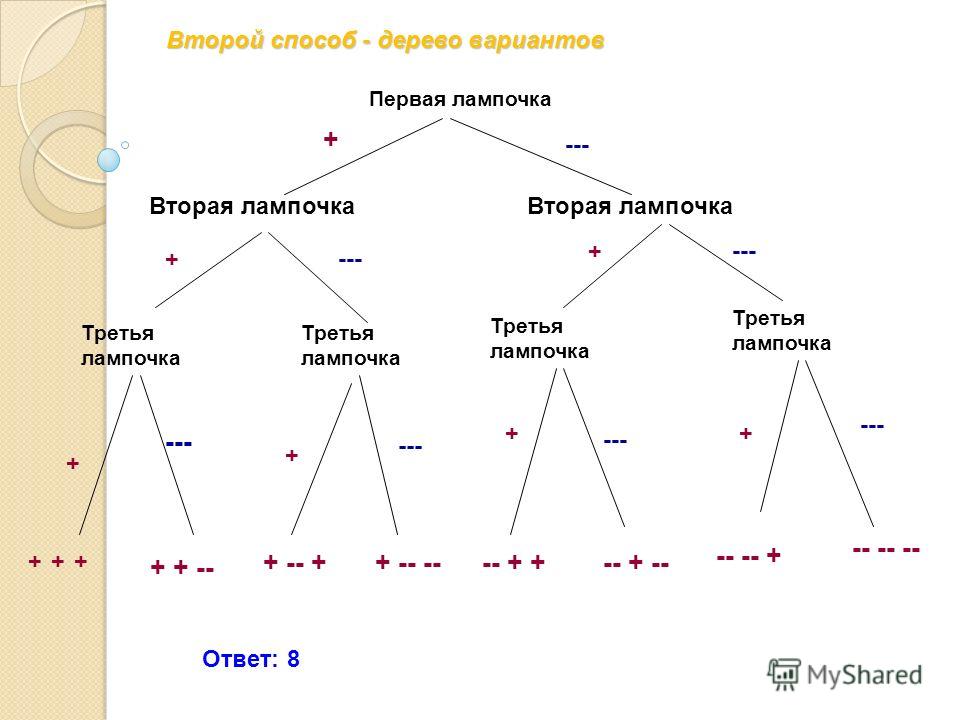
По правилу произведения общее количество вариантов обедов: $2\cdot3\cdot2 = 12$

Построим дерево для перечисления вариантов:

Ответ: 12 вариантов

Комбинаторика в лоскутной технике

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Манукян С.Г. 1

---

1МБОУ школа № 3

Казак А.Д. 1

---

1МБОУ Школа № 3

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.

Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов разложения некоторых предметов. Разные варианты, которые приходится выбирать, складываются в самые различные комбинации. И целый раздел математики, называемый комбинаторикой, занят поиском ответов на вопрос: сколько всего есть комбинаций в том или другом случае.

Комбинаторика — раздел математики, изучающая комбинации и перестановки предметов. На уроках технологии при изготовлении рисунка на кухонных прихватках, из лоскутков ткани геометрической формы, меня заинтересовало сколько разных прихваток можно сшить из трех лоскутков, из четырех лоскутков.

Актуальность:

Сегодня выбором объектов и расположением их в том, или ином порядке приходится заниматься всем. Современный человек должен самостоятельно мыслить, сопоставлять факты, уметь находить различные варианты решения проблем. Умение решать комбинаторные задачи пригодиться ученикам в разных жизненных ситуациях и на многих уроках в школе. Лоскутное шитье во времена экономического кризиса помогает многим людям сохранить семейный бюджет. Комбинации лоскутков различной геометрической формы применяются для создания одежды и предметов интерьера. Накопление опыта решения комбинаторных задач расширяет кругозор, показывает использование комбинаторики в смежных дисциплинах.

Гипотеза:

Комбинаторика имеет широкую практическую направленность в лоскутной техники.

Объект исследования:

Область математики «Комбинаторика» и вид прикладного искусства «Лоскутная техника».

Цель:

Показать широкое применение комбинаторики в одном из видов прикладного искусства – «Лоскутной техники». Выяснить какие комбинаторные методы применяются для перебора вариантов построения комбинаций геометрического рисунка.

Задачи:

Подобрать и изучить литературу о истории развития комбинаторики.

Изучить историю развития «Лоскутной техники».

Провести перебор вариантов построения комбинаций геометрического рисунка при изготовлении кухонных прихваток, а так же объёмных фигур в виде сов.

Проанализировать результаты перебора и результаты подсчета по формулам комбинаторики.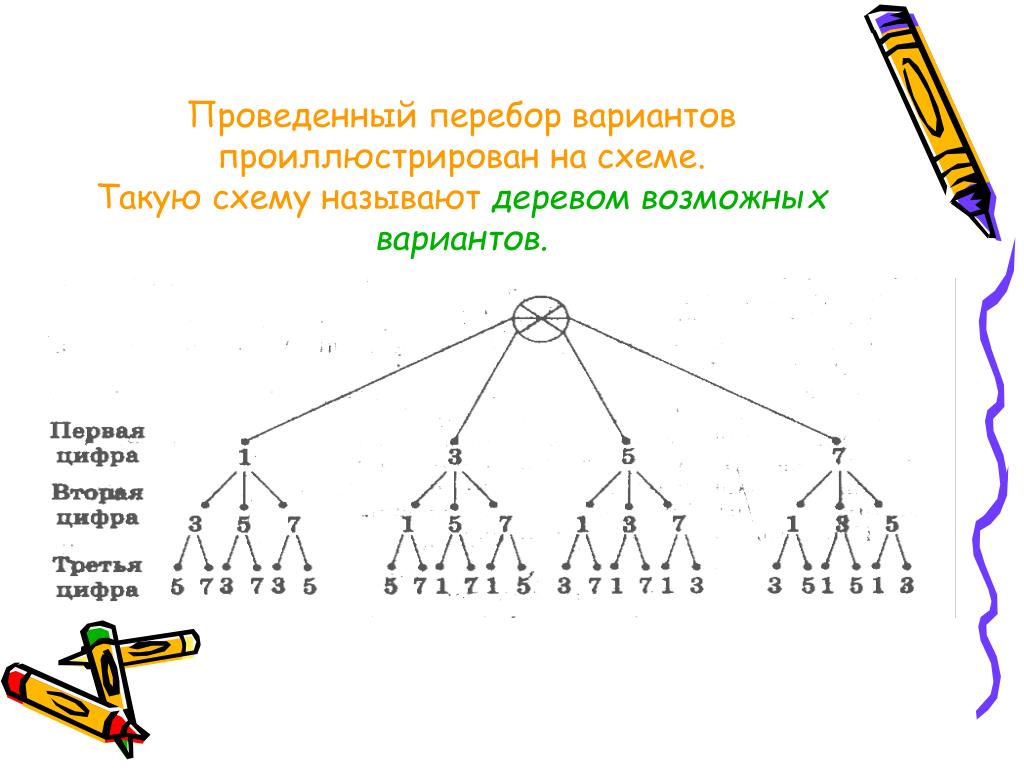

Составить комбинаторные задачи на основе материала с урока технологии.

1. История развития Комбинаторики

Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.

В повседневной жизни нередко перед нами возникают про­блемы, которые имеют не одно, а несколько различных вариан­тов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число. Такого рода задачи называют комбинаторными.

Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, – возникла в XVII в. Долгое время комбинаторика лежала вне основного русла развития математики. На протяжении двух с половиной столетий основную роль в изучении природы играл математический анализ. Процессы, имевшие атомистическую природу, заменялись непрерывными, чтобы можно было применить к ним развитый аппарат математики. Положение коренным образом изменилось после создания быстродействующих вычислительных машин, компьютеров. С их помощью стало возможным делать переборы, ранее требовавшие сотен и тысяч лет. В эпоху расцвета дискретной математики изменилась и роль древнейшей области дискретной математики – комбинаторики.

2. История развития «Лоскутной техники» и лоскутного шитья.

2.1. История развития лоскутной техники

Гурама. .. Пэчворк.. . Квилт. .. Все это — лоскутная техника, корни которой в очень далеком прошлом. Некоторые исследователи называют примерную дату зарождения этого вида бытовой деятельности человека, отсылая нас к девятому веку. Впрочем, некоторые из них считают, что на самом деле это было гораздо раньше. Однако, как бы там ни было, мы знаем, что «лоскутная техника» — это один из видов прикладного искусства, чрезвычайно востребованный сегодня.

В традиции очень многих народов Европы, Азии, Америки это практичное изобретение человечества было связано, прежде всего, с бедностью большей части населения, которая пыталась таким образом решить свои житейские проблемы. И, конечно, нетрудно догадаться, что изобретательницей техники сшивания лоскутков была женщина. Именно она, решая домашний вопрос — во что одеть мужа и детей, додумалась до абсолютно экономичного и оправданного действия: из лоскутков старой, вы шедшей из обихода одежды, создавать новую, а также предметы домашнего обихода в виде одеял, навесов, сумок, подушек и занавесей.

Многие из исследователей склонны предполагать, что впервые этот метод применили англичанки; сшивая из кусочков кожи одежду. Другие утверждают, что этот вид творчества возник все-таки на Востоке и былизвестен в Японии и Китае много тысячелетий назад. Впрочем, это уже дело исследователей — докапываться до самых фантастических деталей и подробностей исторического хода событий — в возникновении и распространении этого рукотворчества по всей планете и отличительных национальных особенностей, ставших основополагающей частью того или иного рисунка. Понятно, что в Африке, Японии или Древней Руси все это выглядело абсолютно по-разному. Но все же объединяющие моменты существуют. Например, практически во всех техниках отмечено наличие геометрического рисунка: квадрат, круг, прямоугольник, треугольник и т.д.

2.2. История развития

Лоскутная мозаика известна очень давно. Ее применяли вместе с другими технологиями шитья, когда создавали одежду и предметы интерьера из ткани. Были найдены аппликации, сделанные 3000 лет назад. Однако лоскутная техника как самостоятельный вид декоративно-прикладного искусства начало развиваться в Англии в первой половине восемнадцатого века.

В семнадцатом веке в Англию начали привозить индийские хлопчатобумажные ткани прекрасных расцветок и узоров. Иметь в доме одеяло индийского производства, богато декорированное вышивкой или набивным рисунком, стало считаться признаком достатка. Появились и подделки — одеяла из хлопчатобумажных индийских тканей, но выполненных на английских мануфактурах. В 1721 г. Правительство Англии издало Акт о сохранении и развитии шерстяных и шелковых мануфактур, запрещающий продавать ситец и изделия из него, произведенные в Индии. Конечно, контрабанду ситца это не остановило, однако он стал дефицитен и очень дорог. Экономные хозяйки, выкроив из дорогого ситца одежду, стали использовать его остатки для других изделий. Так, яркие элементы узора ткани шли на аппликации: их нашивали на льняные или шерстяные полотна. А из мелких лоскутков разноцветных тканей создавали единое полотно по принципу мозаики. Таком образом, лоскутная техника первоначально возникла как способ изготовления рукодельницами модных текстильных предметов интерьера (например, парадных одеял) в домах без большого достатка.

2.3. Лоскутное шитье в Рооссии

Первоначально это было не столько лоскутное шитье в современном понимании этих слов, сколько перешивание, подновление одежды и предметов убранства жилища из лоскутков отслуживших свой срок вещей. Старые вещи разрезались, лоскутки сортировались: все, что годилось для шитья, шло на лоскутные одеяла, занавески; из очень поношенного плели дорожки, шили махровые коврики – половички. Поскольку «мелкоте» — так на Руси называли мальчиков и девочек до шести – восьми лет – новый одежды не полагалось, то русские крестьянки перешивали старые рубашки, на рубашечки для самых маленьких. Да и одежды более взрослых детей шили преимущественно из старой одежды родителей или просто давали донашивать свою. Такая традиция была распространена не только в бедных семьях, но и в зажиточных и даже богатых. Сейчас это может показаться странным, но если учесть, что вся одежда состояла только из натуральных волокон и шилась натуральными нитками, то становится понятным, почем у вещи, послужившие одному поколению, не только не выбрасывались, но и могли пригодиться детям и внукам. Следует сказать, что до восемнадцатого века одежда на Руси была в основном домотканой, то есть изготавливалась из полотна, сотканного на ткацком станке, который был почти в каждой избе.

3.Методы решения Комбинаторных задач

«Особая примета» комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался словами: «Сколькими способами».

В повседневной жизни нередко перед нами возникают про­блемы, которые имеют не одно, а несколько различных вариан­тов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число. Такого рода задачи называют комбинаторными.

Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7 ?

Решение. Для того чтобы не пропустить и не повто­рить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 2 и, наконец, с цифры 7:

11,14,17,41,44,47,71,74,77.

Таким образом, из трех данных цифр можно составить всего 9 различных двузначных чисел.

Дерево возможных вариантов

В задаче мы искали свой способ перебора всех возможных вариантов решения. Однако существует единый подход к реше­нию самых разных комбинаторных задач с помощью составле­ния специальных схем. Внешне такая схема напоминает де­рево, отсюда название — дерево возможных вариантов. При правильном построении дерева ни один из возможных вариан­тов решения не будет потерян.

Вернемся к задаче о составлении двузначных чисел из цифр 1, 4 и 7. Для ее решения построена специальная схема.

Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Знак * изображает корень дерева, ветви дерева — различные варианты решения. Чтобы получить дву­значное число, надо сначала выбрать первую его цифру, а для этого есть три варианта: 1, 4 или 7. Поэтому из точки * проведены три отрезка и на концах поставлены цифры 1, 4 и 7. Затем надо выбрать вторую цифру, а для этого также есть три варианта: 1, 4 или 7. Поэтому от каждой первой цифры прове­дено по три отрезка, на концах которых снова записано 1, 4 или 7.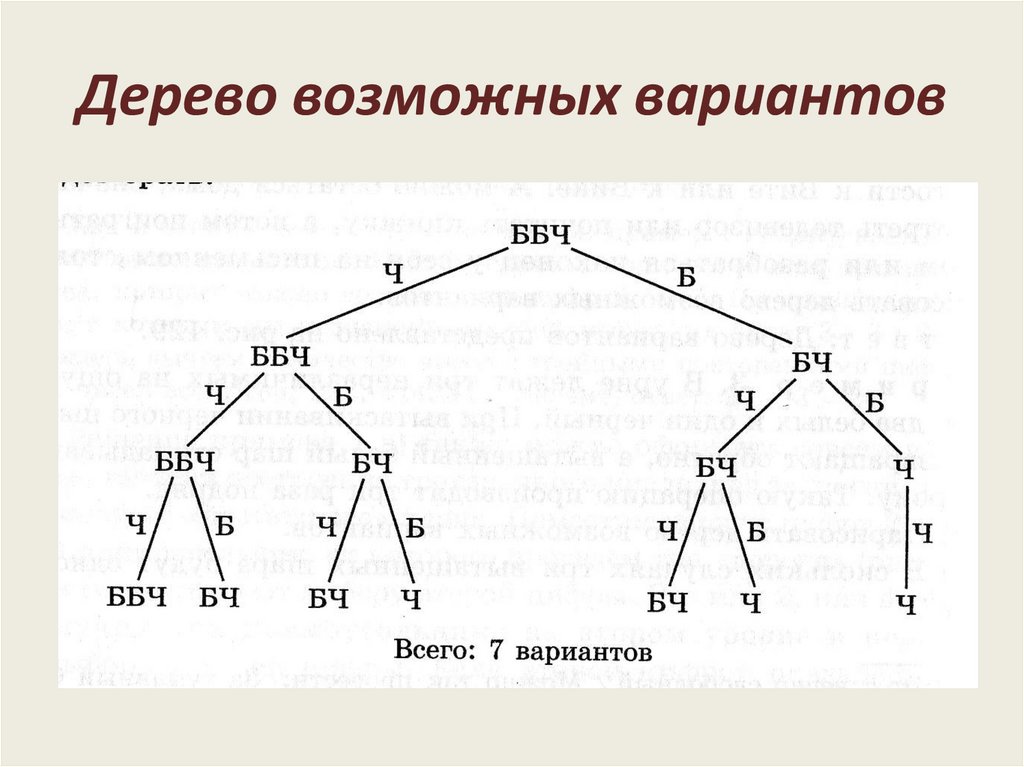 Итак, получено всего 9 различных двузначных чисел. Других двузначных чисел из этих трех цифр составить невозможно.

Посмотрим, как построение дерева помогает решить самые разные комбинаторные задачи.

Задача 2. Школьники из Волгограда собрались на кани­кулы поехать в Москву, посетив по дороге Нижний Новгород. В справочном бюро они получили следующие сведения: из Волгограда в Нижний Новгород можно отправиться на тепло­ходе или поезде, а из Нижнего Новгорода в Москву — на самолете, теплоходе, поезде или автобусе.

Сколькими различными способами могут ребята осущест­вить свое путешествие?

Решение. Изобразим все возможные способы совер­шить путешествие при помощи дерева. При построе­нии дерева использованы следующие обозначения: Т — тепло­ход, П — поезд, С — самолет, А — автобус.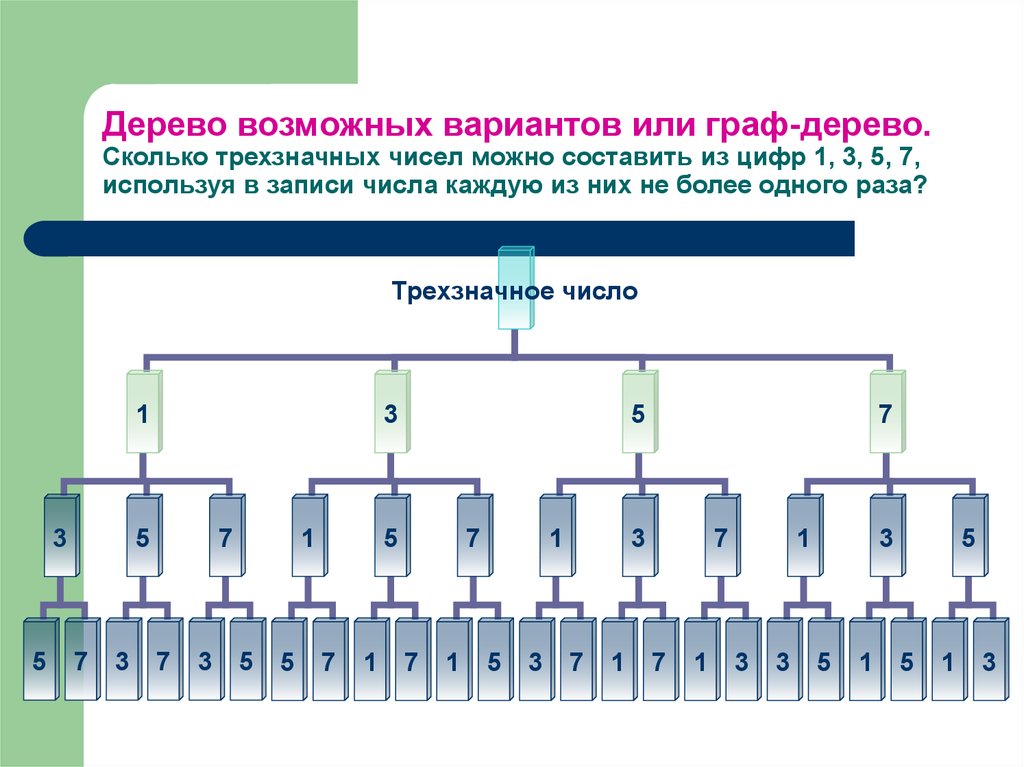

Таким образом, имеется 8 возможных способов добраться из Волгограда в Нижний Новгород и затем в Москву. Из них ребята могут выбрать подходящий по времени и по стоимости.

4. Изготовление кухонных прихваток и объёмных сов

4.1. Перебор вариантов комбинаций геометрического рисунка

На уроке технологии мы решили изготовить кухонные прихватки. Рисунок на прихватках мы будем выполнять из лоскутков ткани, имеющих форму различных геометрических фигур. Я выполняла рисунок из прямоугольников и квадратов разного размера и цвета. Мне стало интересно, сколькими способами я могу составить рисунок на кухонных прихватках.

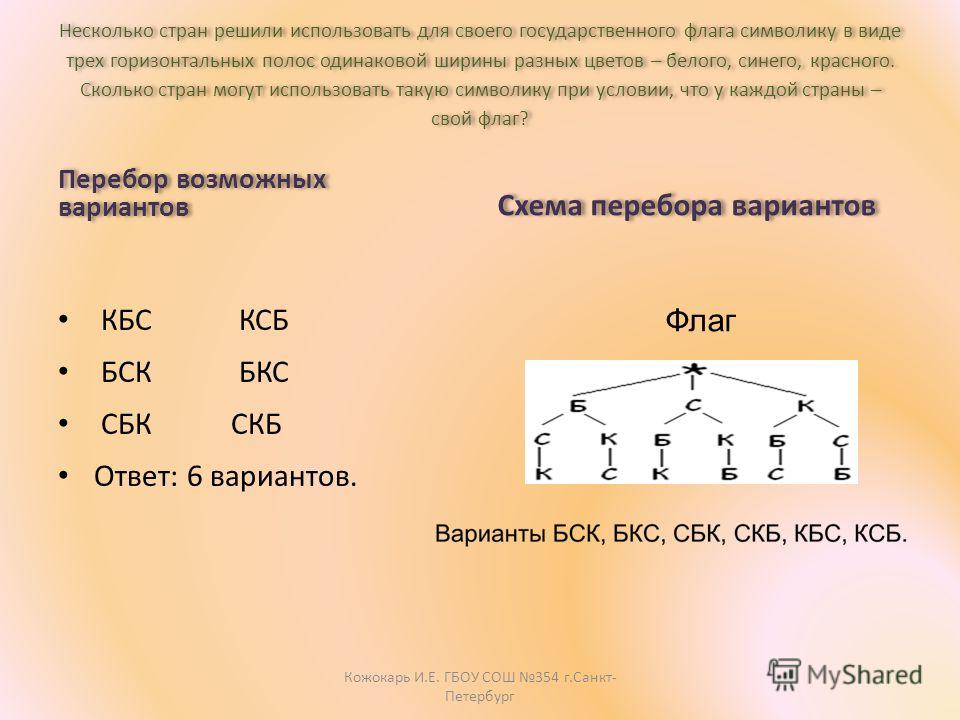
Первая серия прихваток: я взяла 3 лоскутка в форме прямоугольников разного цвета (синий, красный, зеленый). При изготовления рисунка я комбинировала лоскутки по цвету и выбирала для рисунка 2 прямоугольника из 3 прямоугольников.

Чтобы подсчитать все возможные комбинации я составила схему:

У меня получилось 6-ть способов изготовления рисунка на кухонной прихватке.

Вторая серия прихваток: я взяла 3 лоскутка в форме прямоугольников разного цвета (синий, красный, зеленый). При изготовления рисунка я комбинировала лоскутки по цвету и выбирала для рисунка 3 прямоугольника. Для подсчета всевозможных комбинации я снова составила схему ( дерево возможных комбинации)

Первый лоскуток я могу выбрать тремя способами, второй – двумя способами, а третий – только одним. Всего получилось 6 комбинаций.

Мы решили усложнить задачу, изготовив не плоские, а объёмные фигуры (в виде сов) с помощью метода комбинаторики. Для изготовления (Приложение 1) сов мы использовали 3 прямоугольных лоскута, которые разрезали на 8 треугольников каждый. Из полученных теоретических знаний и практических навыках на кухонных прихватках мы знаем, что должно получиться 6 комбинаций сов, отличающихся только раскраской. В итоге нами получены 6 симпатичных сов. Они такие похожие, но такие разные!

4.2. Подсчет вариантов комбинаций геометрического рисунка по формулам

При подсчете возможных комбинаций геометрического рисунка на кухонных прихватках способом составления схем я затратила много времени. А если применить формулы комбинаторики, то вычисление можно упростить и затратить меньше времени.

В зависимости от правил составления комбинаций можно выделить 3 типа комбинаций:

1. Перестановки;

2. Размещения;

3. Сочетания.

Определение: Перестановкой из п элементов называется каждое расположение этих элементов в определенном порядке.

…2*1

При изготовлении рисунка из трех прямоугольников разного цвета можно применить эту формулу

способов

Определение: Размещением из п элементов по к называется любое множество, состоящие из любых к элементов, взятых в определенном порядке из данных п элементов.

По этой формуле можно рассчитать количество комбинаций при изготовлении кухонных прихваток, выбирая из 3-х лоскутков прямоугольной формы по 2 прямоугольника.

способов

При изготовлении кухонных прихваток из 2 квадратов и 2 прямоугольников количество комбинаций можно рассчитать по формуле перестановок

способа

Результаты перебора возможных комбинаций геометрического рисунка на кухонных прихватках и результаты подсчета этих комбинаций по формулам комбинаторики совпали. Использование формул комбинаторики сокращает время подсчета комбинаций.

4.2. Задачи с урока технологии

1. На уроке технологии в нашем классе занимаются 14 девочек. Сколькими способами можно рассадить из на 14 мест?

2. Для изготовления рисунка на круглом коврике взяли лоскутки в виде 6 треугольников разного цвета. Сколькими способами можно составить рисунок из 6 треугольников?

3. К 8 марта были сшиты 10 фартуков. Сколькими способами можно их подарить 10 мамам?

4. В олимпиаде по технологии участвовало 20 учеников. Сколько существует вариантов распределения 3-х призовых мест и одного поощрения?

5. Сколькими способами можно выбрать 3 цветных полоски разного цвета для коврика из 9 лоскутков?

6. Сколькими способами можно рассадить учениц за ручную, ножную и электрическую швейные машины, если всего в группе занимается 14 девочек.

7. Из 14 учениц класса, нужно выбрать 3 ученицы на олимпиаду по технологии. Сколькими способами можно сделать этот выбор?

8. Для изготовления рисунка на лоскутном одеяле взяли 15 кругов и семь квадратов. Рисунок нужно составить из 5 кругов и трех квадратов. Сколькими способами это можно сделать?

Заключение

Работая над этим проектом я расширила свои знания о комбинаторике и лоскутной технике. Я рассмотрела, как можно комбинировать рисунок из нескольких лоскутков различной геометрической формы. Я приобрела опыт решения комбинаторных задач при изготовлении кухонных прихваток с геометрическим рисунком и при изготовлении объёмных фигур, на примере сов.

Рассмотрев использование комбинаторики в одном из видов прикладного искусства – «лоскутной технике», мы показали практическую значимость комбинаторики как области математики. Таким образом мы подтвердили гипотезу: комбинаторика – это раздел математики, который имеет широкую практическую направленность в лоскутной технике.

Я надеюсь, что моя работа заинтересует учащихся, поможет развитию их кругозора, мышления, будет способствовать развитию творчества и умению решать комбинаторные задачи в разных ситуациях в жизни.

Литература

Айгенер М. Комбинаторная теория. М.:Мир,1982.

Алгебра для 9 класса: Учеб. пособие для учащихся шк. и кл.с глуб. изуч. математики/ Н.Я. Виленкина-М.: Просвещение,1999

Бородин А.И.,Бугай А.С. Биографический словарь деятелей в облости математики. Киев: Ряданськая школа, 1979

Бродский Я. Об изучении элементов комбинаторики, вероятности, статистики в школе// Математика.-2004.-№31.

Виленкин Н. Я. Комбинаторика. –М: Просвещение, 1969

Семеновых А. Комбинаторика //Математика. – 2004- №15.

Шейнина О. С., Соловьева Г. М. Математика/О. С. Шейнина, Г. М. Соловьева – М.: Изд-во НЦ ЭНАС, 2007. – 208с.

Энциклопедия для детей. Т.11.Математика / Глав. ред, М.Д.Аксёнова. – М.: Аванта+,1998. – 688 с.: ил.

Приложение 1

Изготовление сов используя свойства комбинаторики

Просмотров работы: 632

8.3: Вероятность с использованием древовидных диаграмм и комбинаций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

37908

• Рупиндер Сехон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе вы научитесь:

1. Использовать диаграммы дерева вероятностей для расчета вероятностей
2. Использовать комбинации для расчета вероятностей

В этом разделе мы применим ранее изученные методы счета для расчета вероятностей и воспользуемся древовидными диаграммами, чтобы лучше понять, о чем идет речь.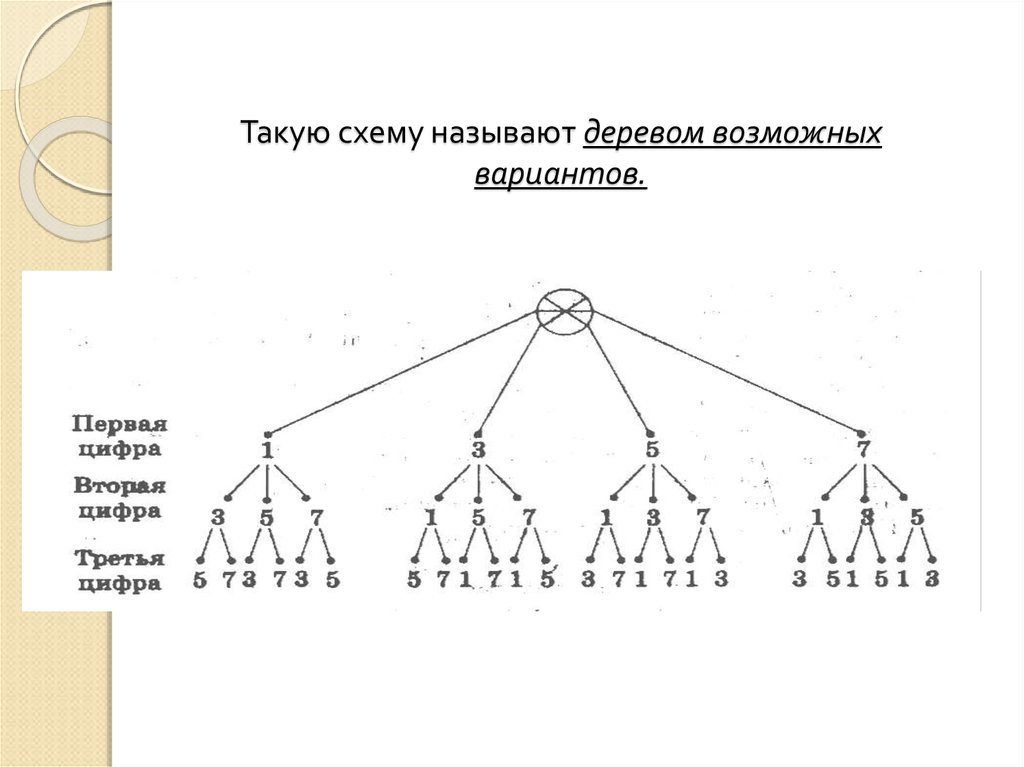

ИСПОЛЬЗОВАНИЕ ДИАГРАММ ДЕРЕВА ДЛЯ ВЫЧИСЛЕНИЯ ВЕРОЯТНОСТЕЙ

Мы уже использовали древовидные диаграммы для перечисления событий в демонстрационном пространстве. Древовидные диаграммы могут быть полезны для организации информации в вероятностных задачах; они помогают обеспечить структуру для понимания вероятности. В этом разделе мы расширяем наше предыдущее использование древовидных диаграмм на ситуации, в которых не все события в демонстрационном пространстве равновероятны.

Мы назначаем соответствующие вероятности событиям, показанным на ветвях дерева.
Перемножая вероятности вдоль пути по дереву, мы можем найти вероятности для «и» событий, которые являются пересечениями событий.

Начнем с примера.

Пример \(\PageIndex{1}\)

Предположим, в банке лежат 3 красных и 4 белых шарика. Если два шарика извлечены с заменой, какова вероятность того, что оба шарика красные?

Решение

Пусть \(\mathrm{E}\) будет событием, что первый вытащенный шарик будет красным, и пусть \(\mathrm{F}\) будет событием, что второй вытащенный шарик будет красным.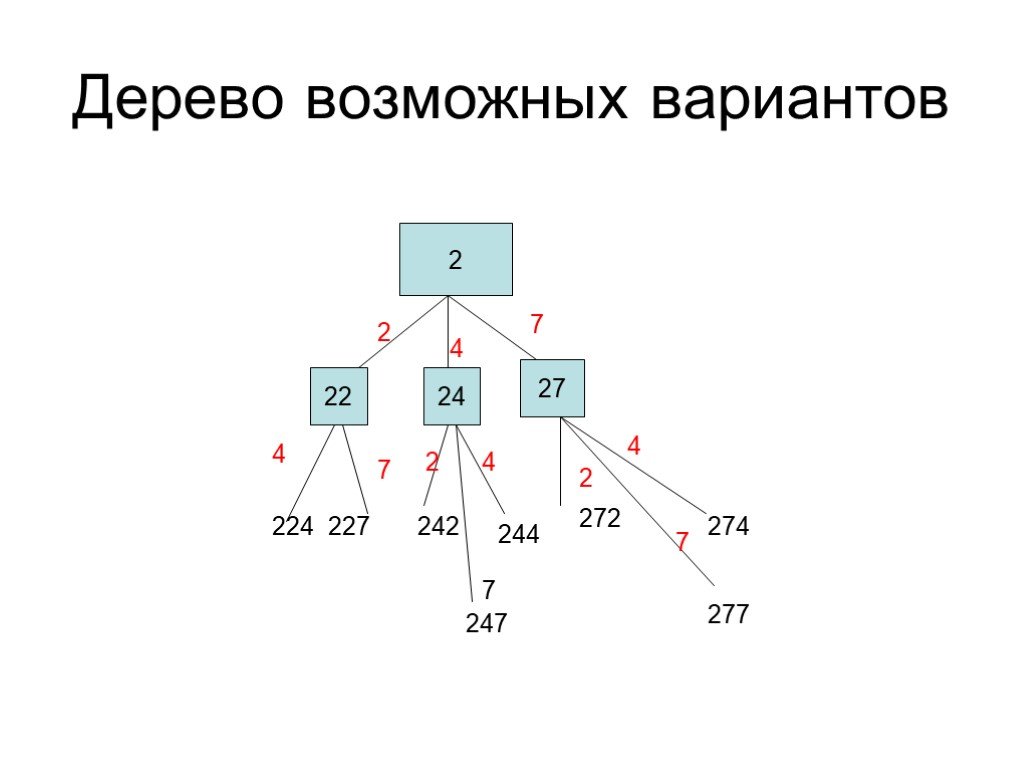

Нам нужно найти \(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).

Под утверждением «два шарика вынимаются с замещением» мы подразумеваем, что первый шарик заменяется до того, как вытащен второй шарик.

В первом розыгрыше есть 7 вариантов. А так как первый шарик ставится на место до того, как вытащен второй, то для второго вытягивания опять же есть семь вариантов. Используя аксиому умножения, мы заключаем, что выборочное пространство \(\mathrm{S}\) состоит из 49 упорядоченных пар. Из 49 упорядоченных пар есть \(3 \times 3 = 9\) упорядоченные пары, которые показывают красный цвет при первом розыгрыше, а также красный цвет при втором розыгрыше. Следовательно,

\[P(E \cap F)=\frac{9}{49} \nonumber \]

Далее обратите внимание, что в данном конкретном случае

\[P(E \cap F)=\frac{9} {49}=\frac{3}{7} \cdot \frac{3}{7} \nonumber \]

, в результате чего в этом примере: \(\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F})\)

Пример \(\PageIndex{2}\)

Если в примере \(\PageIndex{1}\) два шарика вытащены без замены, то какова вероятность того, что оба шарика красные?

Решение

Под утверждением «два шарика вынимаются без возврата» мы имеем в виду, что первый шарик не вынимается до того, как вытащен второй шарик.

Опять же, нам нужно найти \(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).

В первом розыгрыше снова 7 вариантов. А поскольку первый шарик не кладут на место до того, как будет вытащен второй, для второго вытягивания есть только шесть вариантов. Используя аксиому умножения, мы заключаем, что выборочное пространство S состоит из 42 упорядоченных пар. Из 42 упорядоченных пар есть \(3 \times 2 = 6\) упорядоченные пары, которые показаны красным при первом розыгрыше и красным при втором розыгрыше. Следовательно,

\[P(E \cap F)=\frac{6}{42} \nonumber \]

Обратите внимание, что мы можем разбить это вычисление как

\[P(E \cap F)=\frac{ 6}{42}=\frac{3}{7}\cdot\frac{2}{6}\nonumber\].

Здесь 3/7 представляет собой \(\mathrm{P}(\mathrm{E})\), а 2/6 представляет вероятность выпадения красного при втором розыгрыше, учитывая, что в первом розыгрыше выпало красное.

Последнее записывается как \(\mathrm{P}\)(красный на втором | красный на первом) или \(\mathrm{P}(\mathrm{F} | \mathrm{E})\). «|» представляет слово «дано» или «если». Это приводит к тому, что:

\[\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F} | \mathbf{E}) \nonumber \]

Это важный результат, называемый правилом умножения , , который снова появится в следующих разделах.

Теперь продемонстрируем приведенные выше результаты с помощью древовидной диаграммы.

Пример \(\PageIndex{3}\)

Предположим, в банке лежат 3 красных и 4 белых шарика. Если два шарика вытащены без замены, найдите следующие вероятности, используя древовидную диаграмму.

1. Вероятность того, что оба шарика красные.
2. Вероятность того, что первый шарик красный, а второй белый.
3. Вероятность того, что один шарик красный, а другой белый.

Решение

Пусть \(\mathrm{R}\) будет событием, что вытащенный шарик красный, и пусть W будет событием, что вытащенный шарик будет белым.

Рисуем следующую древовидную диаграмму.

1. Вероятность того, что оба шарика красные, равна \(\mathrm{P}(\mathrm{RR})=6/42\)
2. Вероятность того, что первый шарик красный, а второй белый, равна \(\mathrm{P}(\mathrm{RW})=12/42\)
3. . Для вероятности того, что один шарик красный, а другой белый, мы видим, что это может быть удовлетворено, если первый красный, а второй белый, или , если первый белый, а второй красный. «Или» говорит нам, что мы будем использовать правило сложения из раздела 7.2.

Кроме того, события \(\mathrm{RW}\) и \(\mathrm{WR}\) являются взаимоисключающими событиями, поэтому мы используем форму правила сложения, которая применяется к взаимоисключающим событиям.

Следовательно,

\(\mathrm{P}\)(один шарик красный, а другой белый)

\[\begin{array}{l}
=\mathrm{P}(\mathrm{RW } \text { или } \mathrm{WR}) \\
=\mathrm{P}(\mathrm{RW})+\mathrm{P}(\mathrm{WR}) \\
=12 / 42+12 / 42=24 / 42
\end{array} \nonumber \]

ИСПОЛЬЗОВАНИЕ КОМБИНАЦИЙ ДЛЯ ПОИСКА ВЕРОЯТНОСТЕЙ

Хотя древовидные диаграммы дают нам лучшее представление о проблеме, они непрактичны для задач, где есть более двух или трех вещей. выбраны. В таких случаях мы используем концепцию комбинаций, которую мы изучили в предыдущей главе. Этот метод лучше всего подходит для задач, где порядок выбора объектов не важен, и объекты выбираются без замены.

Пример \(\PageIndex{4}\)

Предположим, в банке находятся 3 красных, 2 белых и 3 синих шарика. Если три шарика вытащены без замены, найти следующие вероятности.

1. \(\mathrm{P}\)(два красных и один белый)
2. \(\mathrm{P}\)(по одному каждого цвета)
3. \(\mathrm{P}\)(Нет синего)
4. \(\mathrm{P}\)(хотя бы один синий)

Решение

Предположим, что шарики помечены как \(R_1,R_2,R_3,W_1,W_2,B_1,B_2,B_3\).

а. \(\mathrm{P}\)(Два красных и один белый)

Поскольку мы выбираем 3 шарика из 8, имеется 8\(\mathrm{C}\)3 = 56 возможных комбинаций. Из этих 56 комбинаций есть \(3 \mathrm{C} 2 \times 2 \mathrm{C}1=6\) комбинаций, состоящих из 2 красных и одной белой. Следовательно,

\[P(\text { Два красных и один белый })=\frac{3 \mathrm{C} 2 \times 2 \mathrm{C} 1}{8 \mathrm{C} 3}=\ frac{6}{56} \nonumber. \номер\]

б. \(\mathrm{P}\)(по одному каждого цвета)

Опять же, имеется 8\(\mathrm{C}\)3 = 56 возможных комбинаций. Из этих 56 комбинаций есть \(3 \mathrm{Cl} \times 2 \mathrm{Cl} \times 3 \mathrm{Cl}=18\) комбинаций, состоящих из одного красного, одного белого и одного синего. Следовательно,

\[P(\text {По одному каждого цвета})=\frac{3 \mathrm{C} 1 \times 2 \mathrm{C} 1 \times 3 \mathrm{C} 1}{8 \ mathrm{C} 3}=\frac{18}{56} \nonumber \]

c. \(\mathrm{P}\)(Нет синих)

Есть 5 не синих шариков, поэтому

\[\mathrm{P}(\text { Нет синего })=\frac{5 \mathrm{C} 3}{8 \mathrm{C} 3}=\frac{10}{56}=\frac{ 5}{28} \номер\]

d. \(\mathrm{P}\)(По крайней мере, один синий)

Под «хотя бы одним синим шариком» мы подразумеваем следующее: один синий шарик и два не синих шарика, ИЛИ два синих шарика и один не синий -синий шарик, ИЛИ все три синих шарика. Итак, нам нужно найти сумму вероятностей всех трех случаев.

\[\mathrm{P}(\mathrm{At} \text { минимум один синий })=\mathrm{P}(1 \text { синий } 2 \text { не синий) }+\mathrm{ P}(2 \text { синий, l не синий) }+\mathrm{P}(3\text { синий) } \nonumber \] 9c) = 5/28\), поэтому \(\mathrm{P}(\mathrm{E}) = 1 — 5/28 = 23/28\).

Пример \(\PageIndex{5}\)

Из колоды вытягиваются пять карт. Найти вероятность получения двух пар, то есть двух карт одного достоинства, двух другого достоинства и одной другой карты.

Решение

Сначала решим более легкую задачу — вероятность получения пары королей и дам.

Поскольку в колоде четыре короля и четыре дамы, вероятность получить двух королей, двух дам и еще одну карту равна

\[\mathrm{P}(\mathrm{A} \text { пара королей и дам })=\frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm {C}1}{52 \mathrm{C} 5} \nonumber \]

Чтобы найти вероятность получения двух пар, мы должны рассмотреть все возможные пары.

Поскольку всего имеется 13 значений, то есть тузы, двойки и т. д., существует 13\(\mathrm{C}\)2 различных комбинаций пар.

\[P(\text { Две пары })=13 \mathrm{C} 2 \cdot \frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm{C} 1}{52 \mathrm{C} 5}=.04754 \номер\]

Пример \(\PageIndex{6}\)

В магазин сотовых телефонов поступила партия из 15 сотовых телефонов, включающая 8 iPhone и 7 телефонов Android.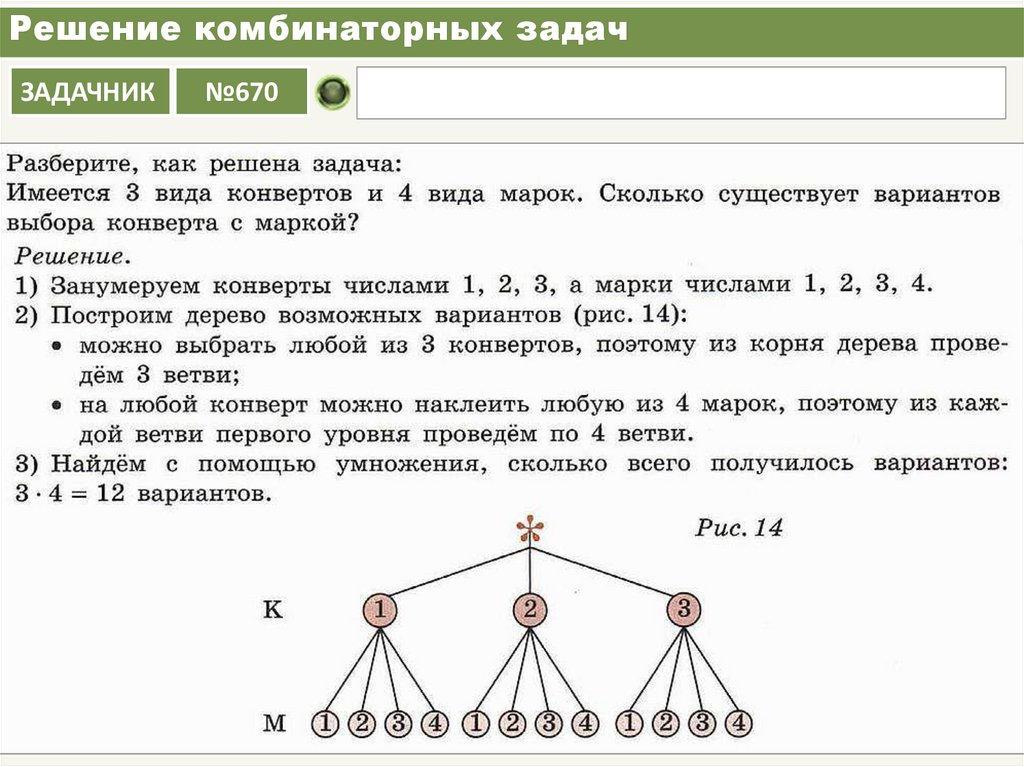 Предположим, что из этой партии случайным образом выбрано 6 сотовых телефонов. Найти вероятность того, что случайно выбранный набор из 6 мобильных телефонов состоит из 2 iPhone и 4 телефонов Android.

Решение

Есть 8\(\mathrm{C}\)2 способов выбрать 2 из 8 iPhone.

и 7\(\mathrm{C}\)4 способа выбора 4 из 7 телефонов Android

Но всего существует 15\(\mathrm{C}\)6 способов выбрать 6 из 15 сотовых телефонов.

Следовательно, у нас есть

\[P(2 \text {iPhone и } 4 \text {телефоны Android})=\frac{8 \mathrm{C} 2 \times 7 \mathrm{C} 4}{15 \ mathrm{C} 6}=\frac{(28)(35)}{5005}=\frac{980}{5005}=0,1958 \nonumber \]

Пример \(\PageIndex{7}\)

Один После обеда в магазине рогаликов осталось 53 рогалика: 20 обычных, 15 с маком и 18 с кунжутом. Предположим, что владелец магазина упаковывает пакет из 9рогалики, которые нужно принести домой на завтрашний завтрак, и выбирает их случайным образом. Найдите вероятность того, что в мешочке 4 простых, 3 маковых и 2 кунжутных семени.

Решение

Существует 20\(\mathrm{C}\)4 способов выбрать 4 из 20 простых рогаликов,

и 15\(\mathrm{C}\)3 способов выбрать 3 из из 15 рогаликов с маком,

и 18\(\mathrm{C}\)2 способов выбрать 2 из 18 рогаликов с кунжутом.

Но всего их 53\(\mathrm{C}\)9способы выбора 9 из 53 рогаликов.

\begin{array}{l}
\mathrm{P} \text{(4 простых, 3 маковых и 2 кунжутных)} &=\frac{20 \mathrm{C} 4 \times 15 \mathrm{ C} 3 \times 18 \mathrm{C} 2}{53 \mathrm{C} 9} \\
&=\frac{(4845)(455)(153)}{4431613550} \\
&=0,761
\end{array}

Мы заканчиваем раздел решением известной задачи под названием Задача дня рождения .

Пример \(\PageIndex{8}\): Задача о дне рождения

Если в комнате 25 человек, какова вероятность того, что по крайней мере у двух человек дни рождения совпадают?

Решение

Пусть событие \(\mathrm{E}\) означает, что по крайней мере у двух людей день рождения совпадает.

Сначала найдем вероятность того, что никакие два человека не имеют одинаковых дней рождения.

Анализируем следующим образом.

Предположим, что в каждом году 365 дней. Согласно аксиоме умножения, у 25 человек может быть 365 90 291 25 90 292 дня рождения. Следовательно, выборочное пространство имеет 365 ²⁵ элемента. Нас интересует вероятность того, что никакие два человека не имеют одинаковых дней рождения. Для первого человека есть 365 возможных вариантов, а поскольку у второго человека день рождения должен быть другим, для второго человека есть 364 варианта, для третьего — 363 и так далее. Следовательно, 9{25}}=.5687\\номер\]

---

Эта страница под заголовком 8.3: Вероятность с использованием древовидных диаграмм и комбинаций распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Рупиндер Сехон и Роберта Блум

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. Правило умножения
   2. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
   3. древовидные диаграммы

Stats Stuff

Древовидная диаграмма полезна для работы с пересечениями событий и условными вероятностями. Дерево состоит из узлов и ветвей, представляющих различные этапы эксперимента. Дерево 1 показывает эксперимент в два этапа с двумя возможными исходами на каждом этапе. На первом этапе это возможности А и А’. Однажды один из те выбраны, варианты на следующем этапе — B и B’.

Узлы представляют начальную точку каждого этапа эксперимента. В Дереве 2 узлы обведены. Ветки — это линии которые распространяются на каждый из результатов на каждом этапе. Ветвь, указывающая, что A’ является результатом первого этапа, показана на дереве толстой зеленой линией. Путь — это последовательность соединенных линий через дерево. У этого дерева четыре пути. Путь, соответствующий исходу А на первом этапе, за которым следует исход B на втором этапе показан пунктирной линией.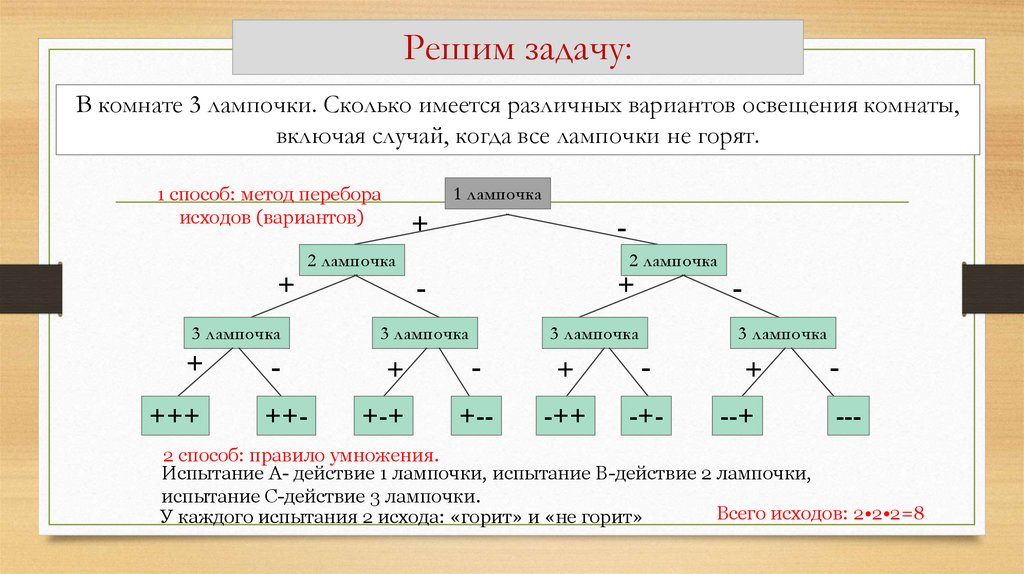

Ветви дерева вероятностей обычно помечаются вероятностями соответствующих событий, как показано на дереве 3. Вероятность, связанная с полным путем через дерево, отмечена справа от дерева и может быть найдена путем умножения вдоль ветви, образующие путь. Для иллюстрации самый верхний путь в дереве соответствует получению исход A на первом этапе и исход B на втором этапе, таким образом, ветви, составляющие путь, представляют P(A) и P(B|A). Полный путь представляет A ∩ B, а вероятность P(A ∩ B) можно найти умножением по ветвям: P(A ∩ B) = P(A)P(B|A).

В дереве вероятностей ветви, исходящие из данного узла, представляют все возможные исходы на данном этапе эксперимента. Таким образом, сумма вероятностей, исходящих из данного узла, должна быть равна 1. В частности, мы видим, что P(A’|B) = 1 — P(A|B).

Пример : Цветовое предпочтение ящерицы

Ученые исследовали, некоторые ящерицы больше терпимы к людям, которые носят выбранный половым путем цвет ящериц (оранжевый). 38,1% попыток исследователей поймать ящерицу были предприняты в синяя рубашка, 33,9% попыток были предприняты в зеленой рубашке, а 28% попыток были предприняты в оранжевой рубашке. Вероятность того, что исследователь одетый в синее успешно поймал ящерицу, составлял 0,627, вероятность того, что исследователь вероятность того, что исследователь в оранжевой одежде успешно поймал ящерицу, равнялась 0,662, а вероятность того, что исследователь, одетый в оранжевую одежду, успешно поймал ящерицу, равнялась 0,803.

Настройте дерево вероятностей для моделирования этого сценария.

Поскольку вероятность поимки зависела от цвета был одет исследователь, цветовые события – исходы на первом этапе и условные события (захват заданного цвета) находятся на втором этапе.

Пример : Предпочтение цвета ящерицы

Используйте дерево, чтобы найти вероятность того, что случайно выбранная попытка поимки была предпринята исследователем. в зеленом и был неудачным ?

Вероятность того, что случайно выбранная попытка захвата была предпринята исследователем в зеленом и оказалась неудачной, равна P(G ∩ C’).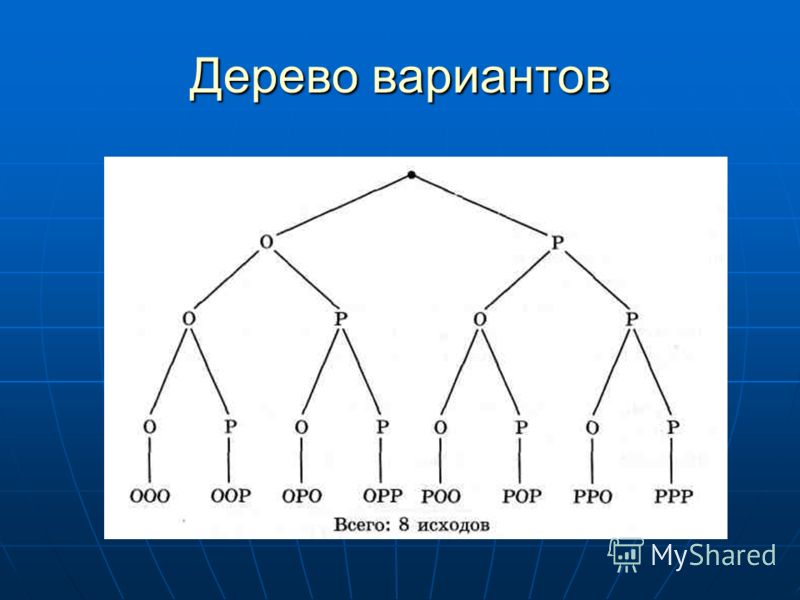 Чтобы найти эту вероятность будем перемножать вероятности, соответствующие ветвям соответствующего пути, выделенным в дереве. То есть P(G ∩ C’) = P(G)P(C’|G). Р(Г) = 0,339и P(C|G) = 0,662. P(C’|G) = 1 – P(C|G) = 1 – 0,662 = 0,338.

P(G ∩C’) = P(G)P(C’|G) = 0,339(0,338) = 0,115.

Вероятность того, что случайно выбранная попытка захвата была предпринята исследователем в зеленом и оказалась неудачной, равна 0,115.

Пример : Предпочтение цвета ящерицы

Какова вероятность того, что любая попытка поимки была успешной?

Вероятность того, что любая попытка захвата была успешной, равна P(C). Все успешные попытки захвата отображаются на дерево путями, которые заканчиваются на C и выделены в дереве. Поскольку эти пути взаимоисключающие, P(C) = P(B ∩ C) + P(G ∩ C) + P(O ∩C).

Чтобы найти вероятность каждого пересечения, умножьте вероятности на соответствующем пути. $ $ \ small{\ begin {массив} {rcl} P (C) & = & P (B) \ cdot P (C | B) + P (G) \ cdot P (C | G) + P (O) \cdot Р(С|О) \\ & = &(0,381 \cdot 0,627) + (0,339 \cdot 0,662) + (0,28 \cdot 0,803)\\ & = & 0,688\end{массив}}$$

Вероятность того, что любая попытка захвата была успешной, равна 0,688.