Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить площадь трапеции.
8 класс
Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить (в см2) площадь трапеции.
Пусть \( ABCD \) — трапеция, \( AC \) — диагональ трапеции и биссектриса острого угла \( \angle A \), т.е. \( \angle BAC=\angle CAD \). \( EF \) — средняя линия трапеции. \( EO=15 \) см, \( OF=33 \) см (\( AC \) пересекает \( EF \) в точке \( O \)). Опустим высоты на \( AD \) из \( B \) и \( C \) (\( BM\perp AD \), \( CK\perp AD \)).
\( S_{ABCD}=\frac{AD+BC}{2}\cdot BM=EF\cdot BM \)
\( EF=EO+OF=15+33=48 \) см
Рассмотрим треугольники \( \triangle ABC \) и \( \triangle ACD \) для которых \( EO \) и \( OF \) являются соответственно средними линиями. Значит \( BC=2\cdot EO=30 \) см, \( AD=2\cdot OF=66 \) см.
2}=\sqrt{900-324}=\sqrt{576}=24 \) см.
Тогда площадь трапеции равна \( S_{ABCD}=48\cdot24=1152 \) см
1152 см2.
8 класс Математика Простая 4174
Продолжить чтение
Формула площади трапеции
Ещё по теме
Найдите \( \cos \alpha \) и \( ctg \alpha \), если \( \sin \alpha=\dfrac{\sqrt3}{2} \) и \( \dfrac{\pi}{2} < \alpha < \pi \).
8 класс Математика Простая 2580
Диагональ равнобокой трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 15 см и 33 см. Вычислить (в см2) площадь трапеции.
8 класс Математика Простая 4174
Дан ромб с диагоналями \(d1=5\) см и \(d2=4\). Найти площадь ромба.
8 класс Математика Простая 1050
Найти конус наибольшего объема, вписанный в шар радиуса \(R.
\)
8 класс Математика Простая 6026
Выразить километры в метрах:
1) 2 километра;
2) 12 километров;
3) 20 километров;
4) 3,7 километра;
5) 8 километров 29 метров;
6) 5 3/20 километра.
8 класс Математика Простая 1628
Пусть \( \overrightarrow{a}=\left\{3,\ 4,2\right\} \), \( \overrightarrow{b}=\{2,\ -1,0\} \). Найти \( \overrightarrow{a}+\overrightarrow{b} \), \( \overrightarrow{a}-\overrightarrow{b} \) и \( 3\overrightarrow{a} \).
8 класс Математика Простая 865
Найти периметр окружности радиуса \( r = 10 \)см.
8 класс Математика Простая 897
В шар радиусом \(a\) вписан цилиндр.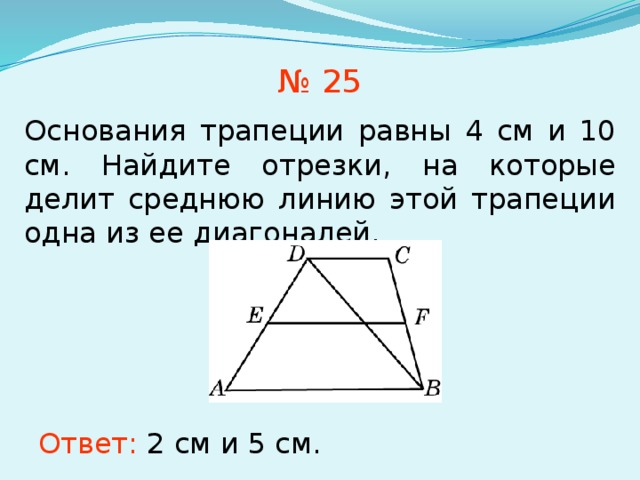
Найти радиус основания \(R\) и высоту \(H\) цилиндра, имеющего наибольший объем.
8 класс Математика Простая 9075
Найти цилиндр с наименьшей площадью поверхности.
8 класс Математика Простая 5201
Конус имеет объем \(V.\) При каком радиусе основания \(R\) и высоте \(H\) площадь боковой поверхности конуса является наименьшей?
8 класс Математика Простая 2192
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Трапеция. Теорема о средней линии трапеции презентация, доклад
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны – боковыми сторонами.
Трапеция называется прямоугольной, если один из ее углов прямой.
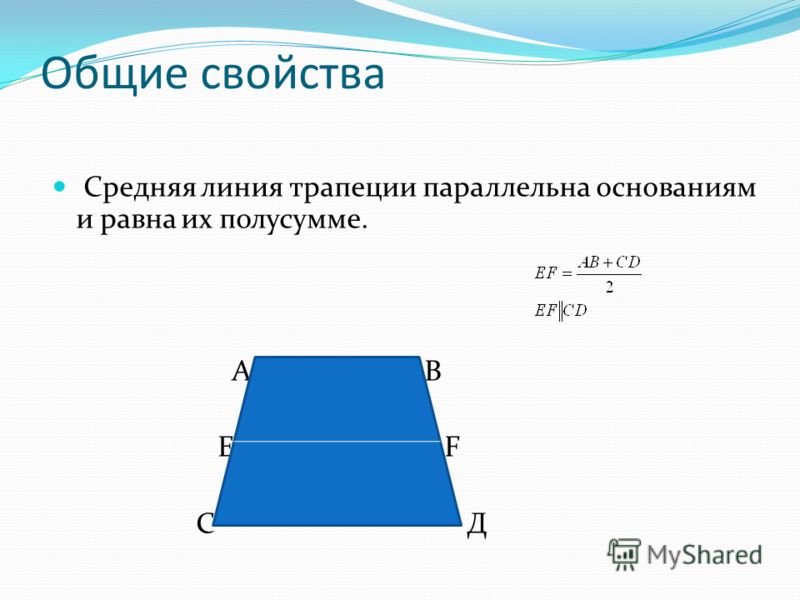
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Теорема о средней линии трапеции
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть EF – средняя линия трапеции ABCD (AB || CD). Проведем прямую DF и ее точку пересечения с прямой AB обозначим G.
Треугольники DFC и GFB равны по второму признаку равенства треугольников (CF = BF по условию, угол 1 равен углу 2, как вертикальные, угол 3 равен углу 4, как накрест лежащие углы). Из равенства этих треугольников следует, что DF = GF и, значит, EF — средняя линия треугольника AGD.
Из теоремы о средней линии треугольника следует, что EF параллельна AB и EF = AG. Так как AB || CD, то EF будет параллельна обоим основаниям и кроме того, EF = AG/2 = (AB + BG)/2 = (AB + CD)/2.
Вопрос 1
Какой четырехугольник называется трапецией?
Ответ: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Вопрос 2
Какие стороны трапеции называются: а) основаниями; б) боковыми сторонами?
Ответ: а) Основаниями трапеции называются ее параллельные стороны;
б) боковыми сторонами трапеции называются ее непараллельные стороны.
Вопрос 3
Какая трапеция называется: а) равнобедренной; б) прямоугольной?
Ответ: а) Трапеция называется равнобедренной, если ее боковые стороны равны;
б) трапеция называется прямоугольной, если один из ее углов прямой.
Вопрос 4
Что называется средней линией трапеции?
Ответ: Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
Вопрос 5
Сформулируйте теорему о средней линии трапеции.
Ответ: Средняя линия трапеции параллельна основаниям и равна их полусумме.
Упражнение 1
Изобразите равнобедренную трапецию ABCD, три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.
Упражнение 2
Изобразите прямоугольную трапецию ABCD, три вершины которой даны на рисунке, а четвертая находится в одном из узлов сетки.
Упражнение 3
Могут ли углы, прилежащие к основанию трапеции, быть один острым, а другой тупым?
Упражнение 4
Может ли у трапеции быть: а) три прямых угла; б) три острых угла?
Ответ: а) Нет;
б) нет.
Упражнение 5
Докажите, что углы при основании равнобедренной трапеции равны.
Доказательство. Пусть ABCD – трапеция, AD не параллельна BC. Докажем, что углы A и B равны.
Через вершину C проведем прямую, параллельную AD и обозначим E ее точку пересечения с прямой AB.
Четырехугольник AECD – параллелограмм, следовательно, угол BAD равен углу BEC. Треугольник BCE – равнобедренный, следовательно, угол BCE равен углу BEC. Таким образом, в трапеции ABCD угол A равен углу B.
Упражнение 6
Верно ли, что если два угла трапеции равны, то она равнобедренная?
Ответ. Нет, она может быть прямоугольной.
Упражнение 7
Верно ли, что если два угла при основании трапеции равны, то она равнобедренная?
Ответ. Да.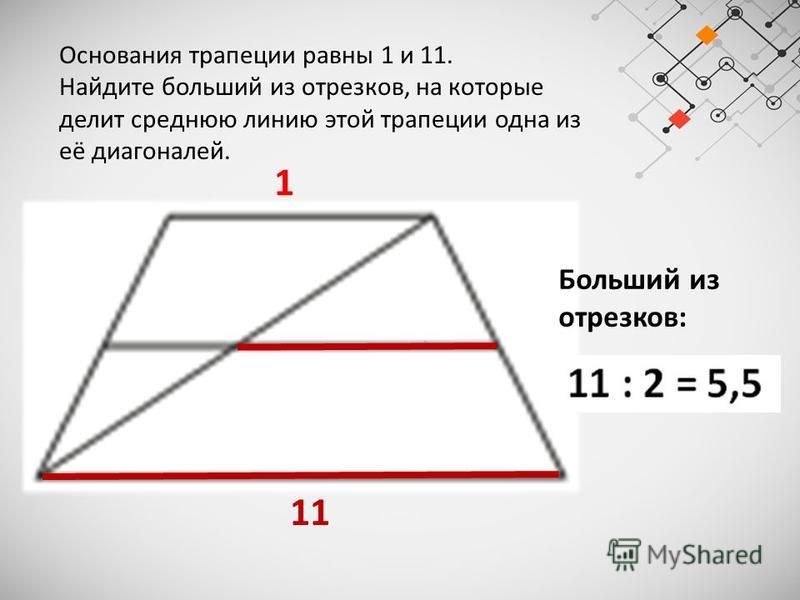
Упражнение 8
Докажите, что сумма двух противоположных углов равнобедренной трапеции равна 180о.
Доказательство. Пусть ABCD – трапеция, AD не параллельна BC. Докажем, что сумма углов A и С равна 180о. Действительно, Сумма углов B и C равна 180о. Угол A равен углу B. Следовательно, сумма углов A и С равна 180о.
Упражнение 9
Чему равны углы равнобедренной трапеции, если известно, что разность противолежащих углов равна 40о?
Ответ: 70о, 110о, 70о, 110о.
Упражнение 10
Докажите, что диагонали равнобедренной трапеции равны.
Доказательство. Пусть ABCD – равнобедренная трапеция. Треугольники ABC и BAD равны (AB – общая сторона, BC = AD, угол ABC равен углу BAD. Следовательно, AC = BD.
Упражнение 11
Верно ли, что если диагонали трапеции равны, то она равнобедренная?
Ответ.
Да.
Упражнение 12
Определите вид четырехугольника, который получится, если последовательно соединить отрезками середины сторон равнобедренной трапеции.
Упражнение 13
Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 3 см, отсекает треугольник, периметр которого равен 15 см. Найдите периметр трапеции.
Ответ: 21 см.
Упражнение 14
Проведите среднюю линию трапеции, изображенной на рисунке.
Упражнение 15
Проведите среднюю линию трапеции, изображенной на рисунке.
Упражнение 16
Основания трапеции относятся как 5:2, а их разность равна 18 см.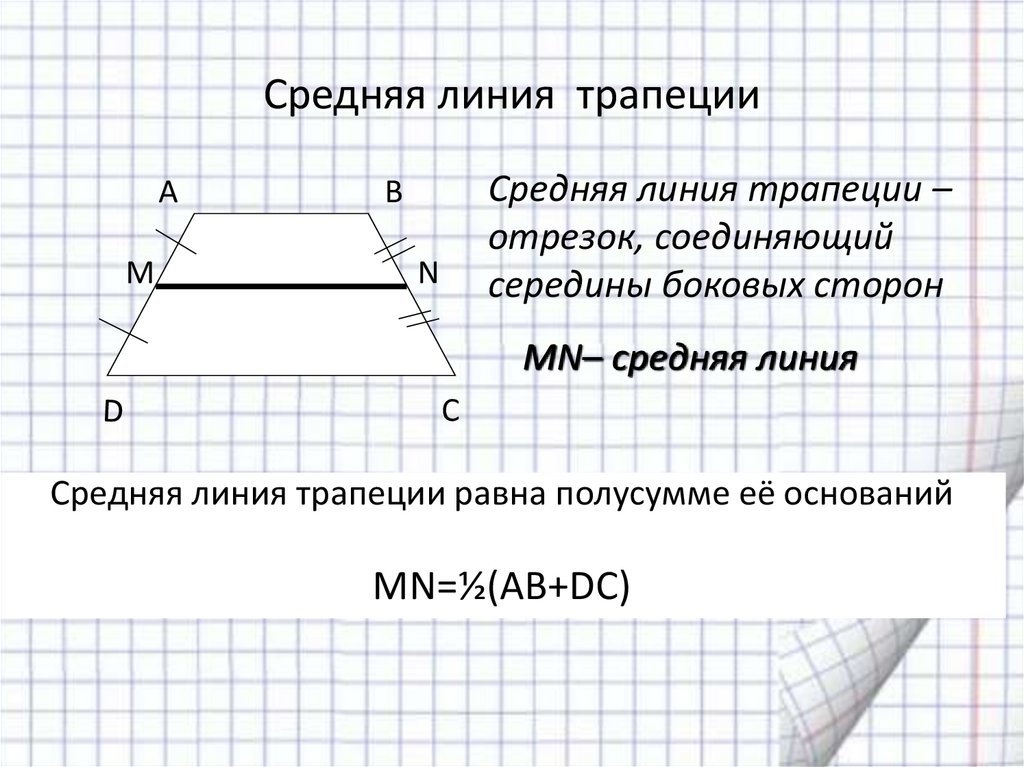
Найдите среднюю линию трапеции.
Ответ: 21 см.
Упражнение 17
Периметр трапеции равен 50 см, а сумма непараллельных сторон равна 20 см. Найдите среднюю линию трапеции.
Ответ: 15 см.
Упражнение 18
Средняя линия трапеции равна 30 см, а меньшее основание равно 20 см. Найдите большее основание.
Ответ: 40 см.
Упражнение 19
Периметр равнобедренной трапеции равен 80 см, ее средняя линия равна боковой стороне. Найдите боковую сторону данной трапеции.
Ответ: 20 см.
Упражнение 20
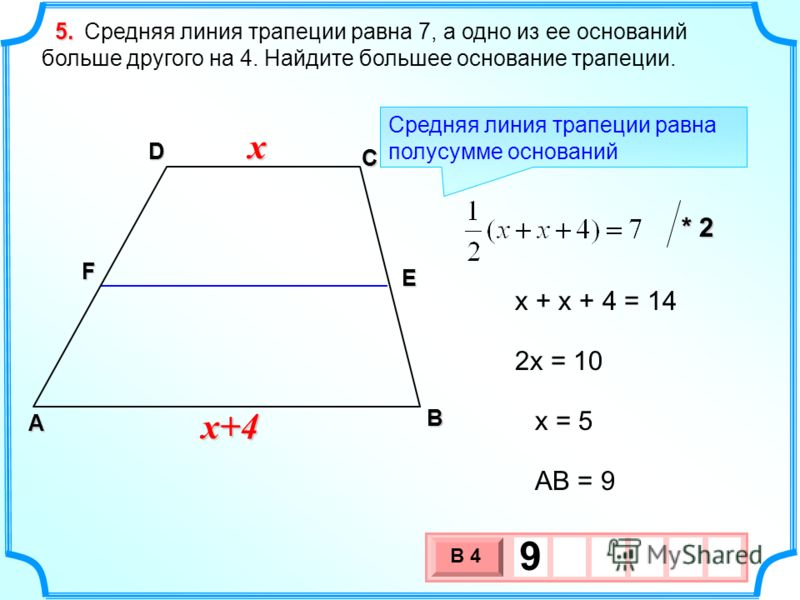
Средняя линия трапеции равна 7 см, а одно из ее оснований больше другого на 4 см. Найдите основания трапеции.
Ответ: 5 см и 9 см.
Упражнение 21
Основания трапеции относятся как 2 : 3, а средняя линия равна 5 м.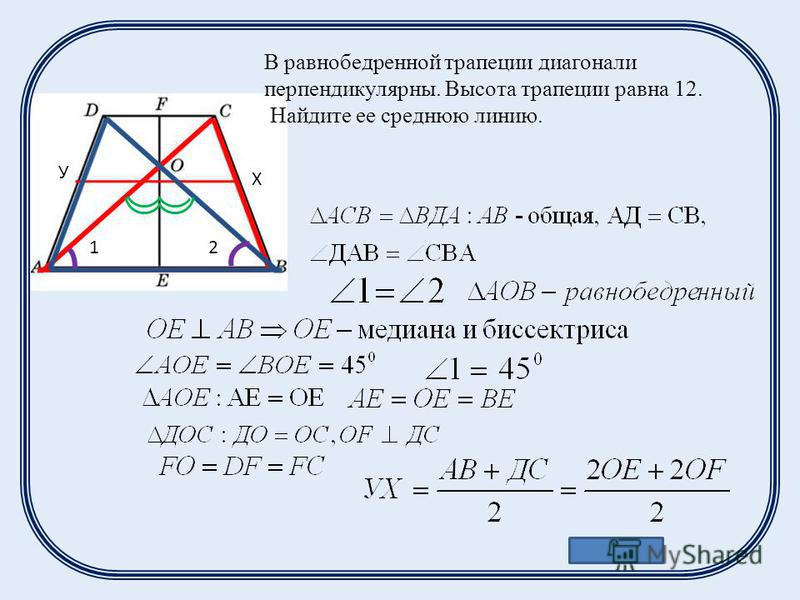
Найдите основания.
Ответ: 4 м и 6 м.
Упражнение 22
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 5 см и 2 см. Найдите среднюю линию этой трапеции.
Ответ: 5 см.
Упражнение 23
В равнобедренной трапеции большее основание равно 2,7 м, боковая сторона равна 1 м, угол между ними 60о. Найдите меньшее основание.
Ответ: 1,7 м.
Упражнение 24
Cредняя линия трапеции равна 10 см. Одна из диагоналей делит ее на два отрезка, разность которых равна 2 см. Найдите основания этой трапеции.
Ответ: 8 см и 12 см.
Упражнение 25
Основания трапеции равны 4 см и 10 см.
Найдите отрезки, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Ответ: 2 см и 5 см.
Упражнение 26
Меньшее основание равнобедренной трапеции равно боковой стороне, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.
Ответ: 60о, 120о, 60о, 120о.
Упражнение 27*
Может ли средняя линия трапеции пройти через точку пересечения диагоналей?
Упражнение 28*
В выпуклом пятиугольнике ABCDE AE = 4. Середины сторон AB и CD, BC и ED соединены отрезками. Середины H и K этих отрезков снова соединены отрезками. Найдите длину отрезка HK.
Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему.
РЕШЕНИЕ: Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему.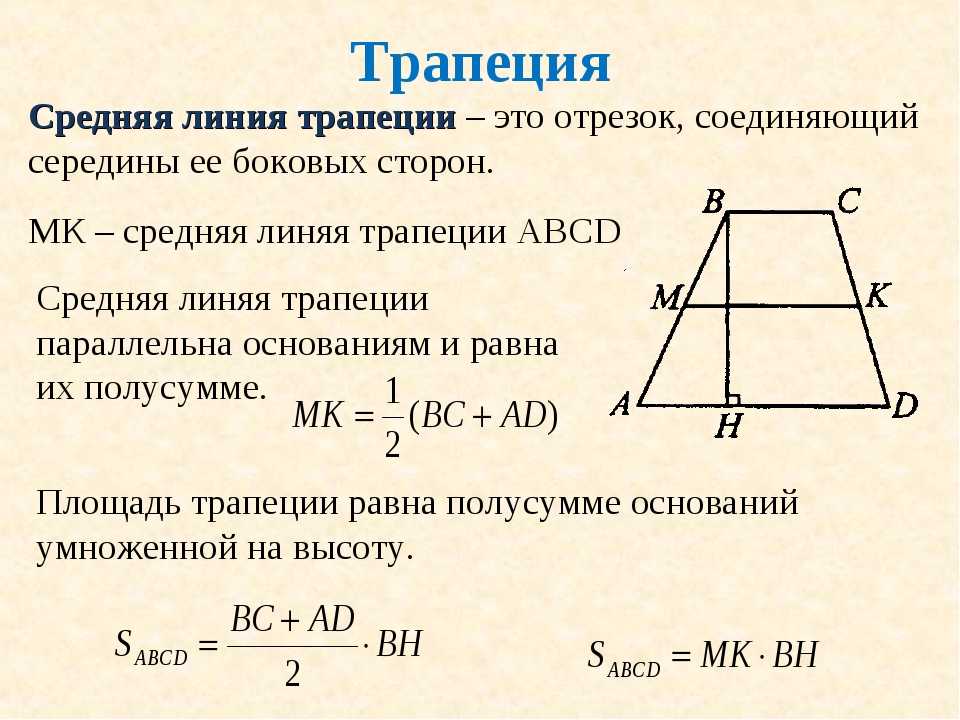
Алгебра -> Настраиваемые средства решения задач Word -> Геометрия -> РЕШЕНИЕ: Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему. Войти
|
|
Объяснить, почему. 
геометрия — Нахождение длины прямой, пересекающей диагонали трапеции.
спросил
Изменено 2 года, 5 месяцев назад
Просмотрено 701 раз
$\begingroup$
В трапеции $ABCD основание $\overline{AB}$ имеет длину 6, а основание $\overline{CD}$ имеет длину 18. Через пересечение диагоналей проходит прямая, параллельная основаниям. Эта прямая пересекает $\overline{AD}$ и $\overline{BC}$ в точках $X$ и $Y,$ соответственно. Найдите $XY.$
Я думал попробовать и получить значение XY.
Я мог бы составить пропорцию, используя медиану. Я действительно не понимаю, как я буду включать длины диагоналей, чтобы найти длину линии, которая пересекается через точку их пересечения.
- геометрия
- конкурс-математика
- четырехугольник
$\endgroup$
1
$\begingroup$
Пусть AC и BD пересекаются в точке O. Тогда подобные треугольники ведут к $\frac{XO}{AB}= \frac{XD}{DA},\>
\frac{XO}{DC}= \frac{XA}{AD}$. Сложите два отношения, чтобы получить$$\frac{XO}{AB}+ \ гидроразрыва {XO} {DC} = 1 $$ что дает $XO = \frac{AB\cdot DC}{AB+DC}=\frac92$. Аналогично, $YO= \frac92$. Таким образом, $XY = XO +YO =9$.
$\endgroup$
$\begingroup$
Пусть пересечение диагоналей равно $O$.
Покажите, что
- $\frac{OA}{OC} = \frac{6}{18}$.
