Диаметр и площадь круга: Формулы, как найти площадь круга

Вычисление площади круга по радиусу. Площадь круга в задаче B5

В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.

Определение площади круга

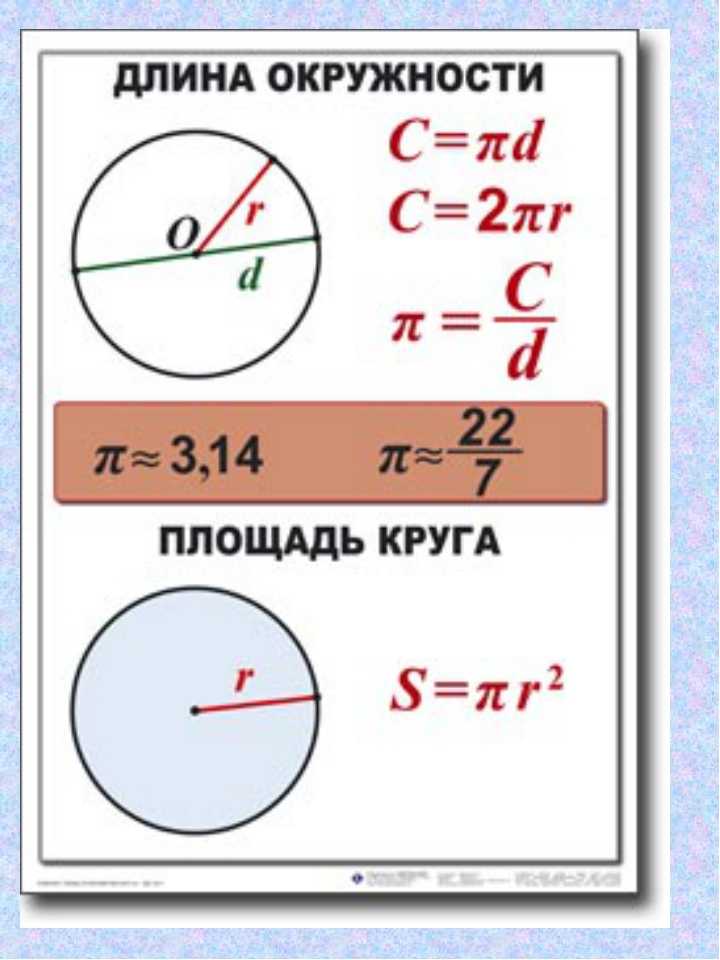
При необходимости площадь круга можно вычислить по формуле:

S

πr 2

D 2

r — радиус круга

D — диаметр круга

S — площадь круга

π — 3.14

Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее.

При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.

Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т.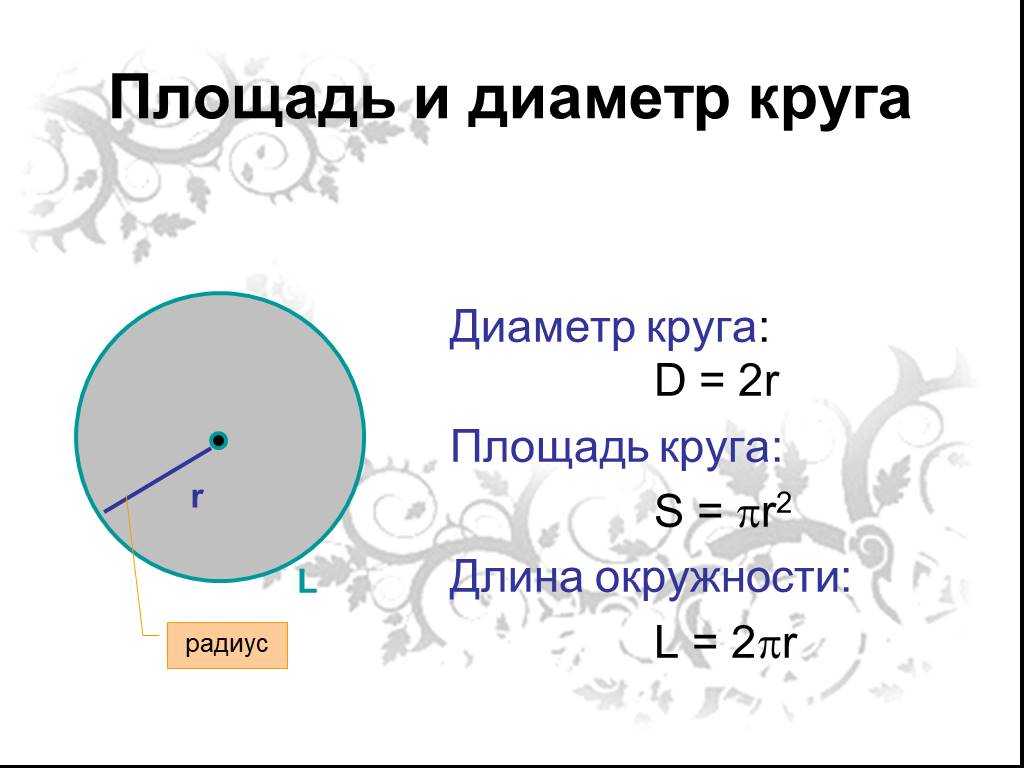

д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.

Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.

Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «

круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.

– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

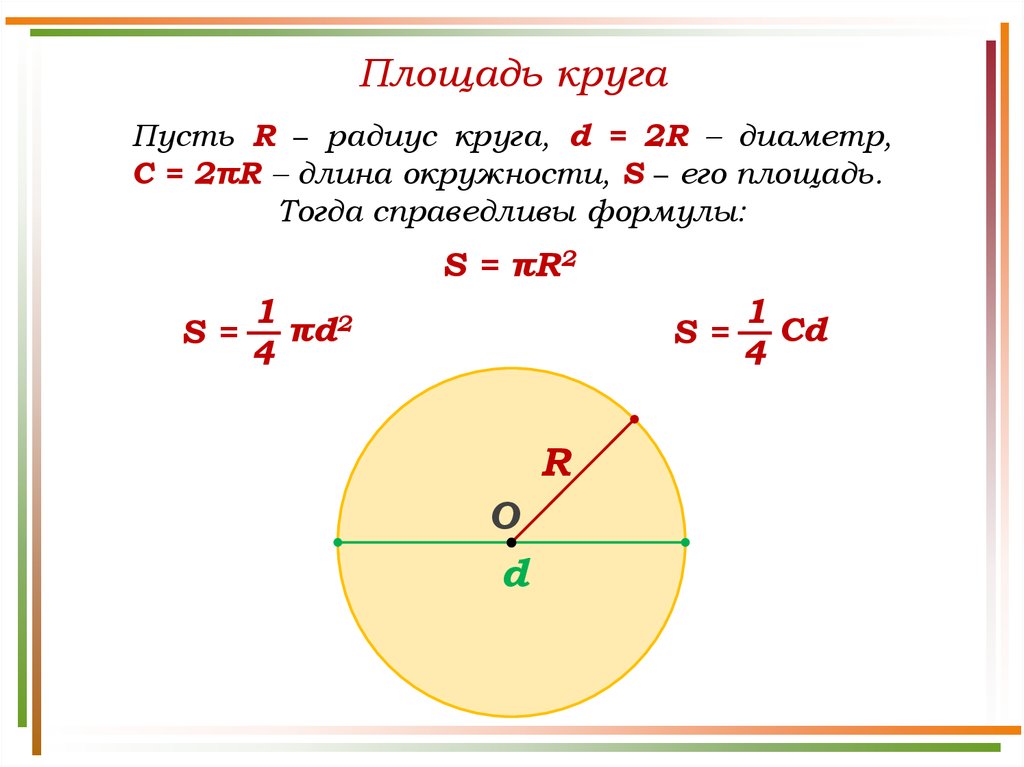
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется

диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..

Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.

Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:

Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.

Площадь нашей окружности будет равна 50,24 кв. см.

Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .

Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.

Теперь используем данные для примера расчета площади круга по приведенной выше формуле:

Как видим, в результате получаем тот же ответ, что и при первых расчетах.

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности.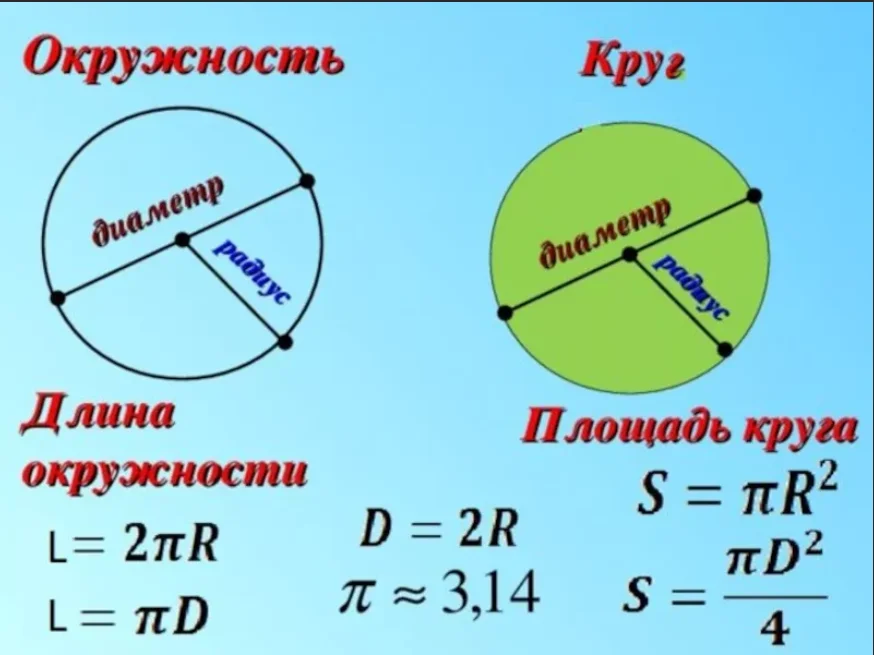 Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:

Итого площадь круга будет равна 5 кв. см.

Площадь круга описанного вокруг квадрата

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра.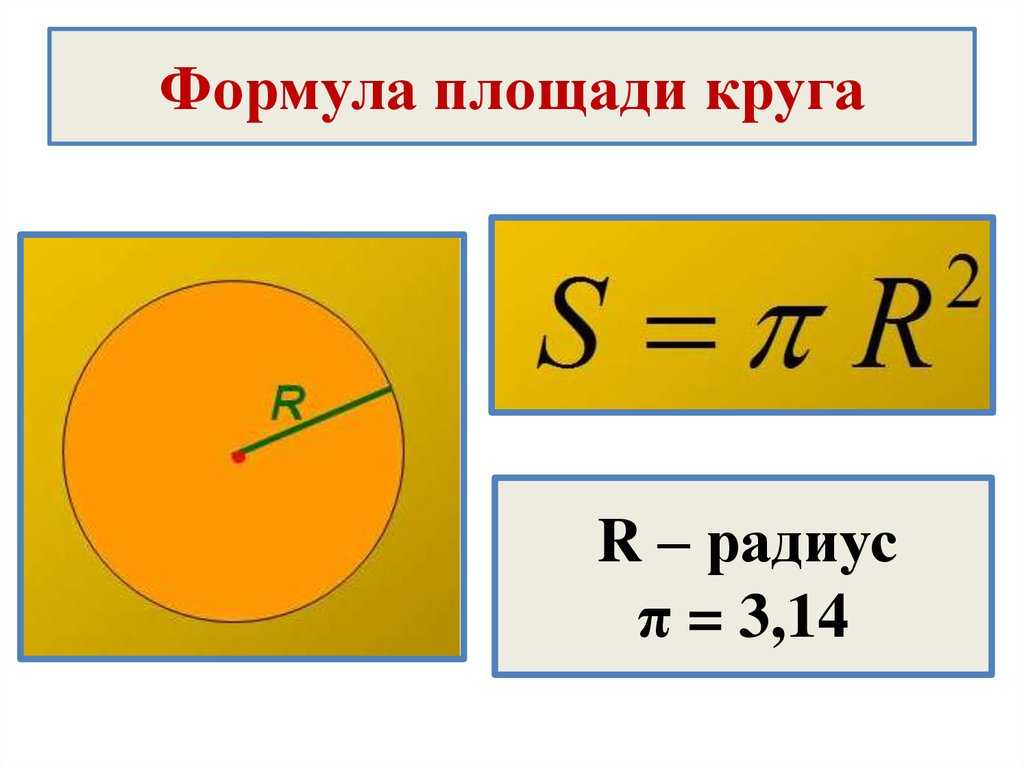 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.

Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.

Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.

Как нам известно из школьной программы, кругом принято называть плоскую геометрическую фигуру, которая состоит из множества точек, равноудалённых от центра фигуры. Так как все они находятся на одинаковом расстоянии, они формируют окружность.

Удобная навигация по статье:

Отрезок, соединяющий центр круга и точки его окружности называют радиусом.

2}/{4*3,14}=64/{12,56}=5. И получаем площадь круга равную пяти квадратным сантиметрам.

Площадь круговых формул

Магистр. круга по площади.

Найдите площадь круга, диаметр которого равен 10 единицам.

Зная диаметр, площадь можно найти двумя способами.

Вариант 1. Используйте формулу,

3,14/4 = 0,785

квадрат диаметр, 10 квадрат = 100

.785 * 100 ≈ 78,5 Единиц. Разделите диаметр на 2, чтобы найти Radius

10/2 = 5

, затем использование,

π * r * r

π * 5 * 5 = π25

3.14 * 25 ≈ 78.5 единицы в квадрате 

Что делать, если известна площадь круга и требуется узнать радиус?

Найдите площадь круга, используя длину окружности.

Найдите площадь круга с длиной окружности 20 π единиц.

Шаг 1. Найдите радиус круга с использованием окружности = 2 πr

20 π = 2 πr

Разделите каждую сторону на π

20/ π = 2 πr/ π

20= 2r

Разделить на 2 обе стороны

20/2 = 2r/2

10 = радиус

Шаг 2.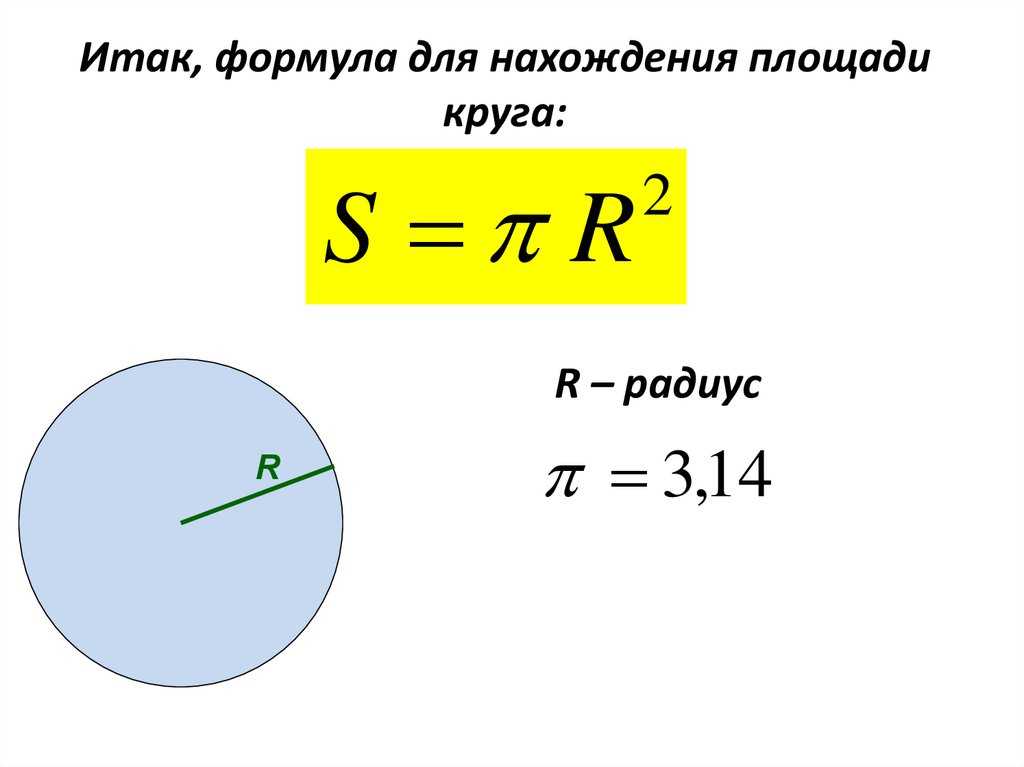   Теперь подставьте радиус 10 в формулу площади.

Площадь = π* 10 *10 = 100 π или 3,14*100 ≈ 314 единиц в квадрате

Найдите площадь круга с радиусом 4 единицы.

Подключите вашу информацию в область круговой формулы:

или π*r*r

π*4*4 = π16 Квадрат. квадрат — примерный ответ.

Найдите площадь круга с радиусом 8 единиц.

π * 8*8 = π64

3,14* 64 ≈ 200,96 единиц в квадрате

Если дана длина окружности, используйте двухэтапный процесс.

Шаг 1.  Найти радиус по окружности, используя,

Радиус = длина окружности/ π

Шаг 2.  После нахождения диаметра используйте формулу

,

Существует несколько формул для нахождения площади круга на основе предоставленной информации.

If the radius is given use, 

Common Core Standard: 7.G.4   7th Grade Math

Finding the area of ​​a circle step шаг за шагом.