Дискретная случайная величина примеры: Дискретные случайные величины. Пример решения задачи на Викиматик

Дискретные случайные величины. Пример решения задачи на Викиматик

Случайной величиной называют переменную величину, которая в результате каждого испытания принимает одно заранее неизвестное значение, зависящее от случайных причин. Случайные величины обозначают заглавными латинскими буквами: $X,\ Y,\ Z,\ \dots $ По своему типу случайные величины могут быть дискретными и непрерывными.

Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.

Пример 1. Приведем примеры дискретных случайных величин:

а) число попаданий в мишень при $n$ выстрелах, здесь возможные значения $0,\ 1,\ \dots ,\ n$.

б) число выпавших гербов при подкидывании монеты, здесь возможные значения $0,\ 1,\ \dots ,\ n$.

в) число прибывших кораблей на борт (счетное множество значений).

г) число вызовов, поступающих на АТС (счетное множество значений).

Содержание

1. Закон распределения вероятностей дискретной случайной величины.

Дискретная случайная величина $X$ может принимать значения $x_1,\dots ,\ x_n$ с вероятностями $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Соответствие между этими значениями и их вероятностями называется законом распределения дискретной случайной величины. Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.

$\begin{array}{|c|c|}
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end{array}$

Пример 2. Пусть случайная величина $X$ — число выпавших очков при подбрасывании игрального кубика. Такая случайная величина $X$ может принимать следующие значения $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятности всех этих значений равны $1/6$. Тогда закон распределения вероятностей случайной величины $X$:

$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$

Замечание. Поскольку в законе распределения дискретной случайной величины $X$ события $1,\ 2,\ \dots ,\ 6$ образуют полную группу событий, то в сумме вероятности должны быть равны единице, то есть $\sum{p_i}=1$.

2. Математическое ожидание дискретной случайной величины.

Математическое ожидание случайной величины задает ее «центральное» значение. Для дискретной случайной величины математическое ожидание вычисляется как сумма произведений значений $x_1,\dots ,\ x_n$ на соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$, то есть: $M\left(X\right)=\sum^n_{i=1}{p_ix_i}$. В англоязычной литературе используют другое обозначение $E\left(X\right)$.

Свойства математического ожидания $M\left(X\right)$:

$M\left(X\right)$ заключено между наименьшим и наибольшим значениями случайной величины $X$.
Математическое ожидание от константы равно самой константе, т.е. $M\left(C\right)=C$.
Постоянный множитель можно выносить за знак математического ожидания: $M\left(CX\right)=CM\left(X\right)$.
Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$.

Пример 3. Найдем математическое ожидание случайной величины $X$ из примера $2$.

$$M\left(X\right)=\sum^n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$

Можем заметить, что $M\left(X\right)$ заключено между наименьшим ($1$) и наибольшим ($6$) значениями случайной величины $X$.

Пример 4. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=2$. Найти математическое ожидание случайной величины $3X+5$.

Используя вышеуказанные свойства, получаем $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2+5=11$.

Пример 5. Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=4$. Найти математическое ожидание случайной величины $2X-9$.

Используя вышеуказанные свойства, получаем $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4-9=-1$.

3. Дисперсия дискретной случайной величины.

Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений. Например, в двух студенческих группах средний балл за экзамен по теории вероятностей оказался равным 4, но в одной группе все оказались хорошистами, а в другой группе — только троечники и отличники. Поэтому возникает необходимость в такой числовой характеристике случайной величины, которая бы показывала разброс значений случайной величины вокруг своего математического ожидания. Такой характеристикой является дисперсия.

Дисперсия дискретной случайной величины $X$ равна:

$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}.\ $$

В англоязычной литературе используются обозначения $V\left(X\right),\ Var\left(X\right)$. Очень часто дисперсию $D\left(X\right)$ вычисляют по формуле $D\left(X\right)=\sum^n_{i=1}{p_ix^2_i}-{\left(M\left(X\right)\right)}^2$.

Свойства дисперсии $D\left(X\right)$:

Дисперсия всегда больше или равна нулю, т.е. $D\left(X\right)\ge 0$.
Дисперсия от константы равна нулю, т.е. $D\left(C\right)=0$.
Постоянный множитель можно выносить за знак дисперсии при условии возведения его в квадрат, т.е. $D\left(CX\right)=C^2D\left(X\right)$.
Дисперсия суммы независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$.
Дисперсия разности независимых случайных величин равна сумме их дисперсий, т.е. $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$.

Пример 6. Вычислим дисперсию случайной величины $X$ из примера $2$.

$$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2}={{1}\over {6}}\cdot {\left(1-3,5\right)}^2+{{1}\over {6}}\cdot {\left(2-3,5\right)}^2+\dots +{{1}\over {6}}\cdot {\left(6-3,5\right)}^2={{35}\over {12}}\approx 2,92.$$

Пример 7. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=2$. Найти дисперсию случайной величины $4X+1$.

Используя вышеуказанные свойства, находим $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0=16D\left(X\right)=16\cdot 2=32$.

Пример 8. Известно, что дисперсия случайной величины $X$ равна $D\left(X\right)=3$. Найти дисперсию случайной величины $3-2X$.

Используя вышеуказанные свойства, находим $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.

4. Функция распределения дискретной случайной величины.

Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.

Функцией распределения случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X < x\right)$

Свойства функции распределения:

$0\le F\left(x\right)\le 1$.
Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha < X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
$F\left(x\right)$ — неубывающая.
${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.

Пример 9. Найдем функцию распределения $F\left(x\right)$ для закона распределения дискретной случайной величины $X$ из примера $2$.

$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$

Если $x\le 1$, то, очевидно, $F\left(x\right)=0$ (в том числе и при $x=1$ $F\left(1\right)=P\left(X < 1\right)=0$).

Если $1 < x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

Если $2 < x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

Если $3 < x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

Если $4 < x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

Если $5 < x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

Если $x > 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+1/6+1/6=1$.

Итак, $F(x)=\left\{\begin{matrix}
0,\ при\ x\le 1,\\
1/6,при\ 1 < x\le 2,\\
1/3,\ при\ 2 < x\le 3,\\
1/2,при\ 3 < x\le 4,\\
2/3,\ при\ 4 < x\le 5,\\
5/6,\ при\ 4 < x\le 5,\\
1,\ при\ x > 6.
\end{matrix}\right.$

График функции распределения $F\left(x\right)$:

Законы распределения дискретных случайных величин

Можно выделить наиболее часто встречающиеся законы распределения дискретных случайных величин:

Биномиальный закон распределения
Пуассоновский закон распределения
Геометрический закон распределения
Гипергеометрический закон распределения

Для данных распределений дискретных случайных величин расчет вероятностей их значений, а также числовых характеристик (математическое ожидание, дисперсия, и т.д.) производится по определенных «формулам». Поэтому очень важно знать данные типы распределений и их основные свойства.

1. Биномиальный закон распределения.

Дискретная случайная величина $X$ подчинена биномиальному закону распределения вероятностей, если она принимает значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$. Фактически, случайная величина $X$ — это число появлений события $A$ в $n$ независимых испытаний Бернулли. Закон распределения вероятностей случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end{array}$

Для такой случайной величины математическое ожидание $M\left(X\right)=np$, дисперсия $D\left(X\right)=np\left(1-p\right)$.

Пример. В семье двое детей. Считая вероятности рождения мальчика и девочки равными $0,5$, найти закон распределения случайной величины $\xi $ — числа мальчиков в семье.

Пусть случайная величина $\xi $ — число мальчиков в семье. Значения, которые может принимать $\xi :\ 0,\ 1,\ 2$. Вероятности этих значений можно найти по формуле $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot {\left(1-p\right)}^{n-k}$, где $n=2$ — число независимых испытаний, $p=0,5$ — вероятность появления события в серии из $n$ испытаний. Получаем:

$P\left(\xi =0\right)=C^0_2\cdot {0,5}^0\cdot {\left(1-0,5\right)}^{2-0}={0,5}^2=0,25;$

$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot {\left(1-0,5\right)}^{2-1}=2\cdot 0,5\cdot 0,5=0,5;$

$P\left(\xi =2\right)=C^2_2\cdot {0,5}^2\cdot {\left(1-0,5\right)}^{2-2}={0,5}^2=0,25.$

Тогда закон распределения случайной величины $\xi $ есть соответствие между значениями $0,\ 1,\ 2$ и их вероятностями, то есть:

$\begin{array}{|c|c|}
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi ) & 0,25 & 0,5 & 0,25 \\
\hline
\end{array}$

Сумма вероятностей в законе распределения должна быть равна $1$, то есть $\sum _{i=1}^{n}P(\xi _{{\rm i}} )=0,25+0,5+0,25=1 $.

Математическое ожидание $M\left(\xi \right)=np=2\cdot 0,5=1$, дисперсия $D\left(\xi \right)=np\left(1-p\right)=2\cdot 0,5\cdot 0,5=0,5$, среднее квадратическое отклонение $\sigma \left(\xi \right)=\sqrt{D\left(\xi \right)}=\sqrt{0,5}\approx 0,707$.

2. Закон распределения Пуассона.

Если дискретная случайная величина $X$ может принимать только целые неотрицательные значения $0,\ 1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.

Замечание. Особенность этого распределения заключается в том, что мы на основании опытных данных находим оценки $M\left(X\right),\ D\left(X\right)$, если полученные оценки близки между собой, то у нас есть основание утверждать, что случайная величина подчинена закону распределения Пуассона.

Пример. Примерами случайных величин, подчиненных закону распределения Пуассона, могут быть: число автомашин, которые будут обслужены завтра автозаправочной станцией; число бракованных изделий в произведенной продукции.

Пример. Завод отправил на базу $500$ изделий. Вероятность повреждения изделия в пути равна $0,002$. Найти закон распределения случайной величины $X$, равной числу поврежденных изделий; чему равно $M\left(X\right),\ D\left(X\right)$.

Пусть дискретная случайная величина $X$ — число поврежденных изделий. Такая случайная величина подчинена закону распределения Пуассона с параметром $\lambda =np=500\cdot 0,002=1$. Вероятности значений равны $P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.

$P\left(X=0\right)={{1^0}\over {0!}}\cdot e^{-1}=0,368;$

$P\left(X=1\right)={{1^1}\over {1!}}\cdot e^{-1}=0,368;$

$P\left(X=2\right)={{1^2}\over {2!}}\cdot e^{-1}=0,184;$

$P\left(X=3\right)={{1^3}\over {3!}}\cdot e^{-1}=0,061;$

$P\left(X=4\right)={{1^4}\over {4!}}\cdot e^{-1}=0,015;$

$P\left(X=5\right)={{1^5}\over {5!}}\cdot e^{-1}=0,003;$

$P\left(X=6\right)={{1^6}\over {6!}}\cdot e^{-1}=0,001;$

…

$P\left(X=k\right)={{{\lambda }^k}\over {k!}}\cdot e^{-\lambda }$

Закон распределения случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & … & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & … & {{{\lambda }^k}\over {k!}}\cdot e^{-\lambda } \\
\hline
\end{array}$

Для такой случайной величины математическое ожидание и дисперсия равным между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda =1$.

3. Геометрический закон распределения.

Если дискретная случайная величина $X$ может принимать только натуральные значения $1,\ 2,\ \dots ,\ n$ с вероятностями $P\left(X=k\right)=p{\left(1-p\right)}^{k-1},\ k=1,\ 2,\ 3,\ \dots $, то говорят, что такая случайная величина $X$ подчинена геометрическому закону распределения вероятностей. Фактически, геометрическое распределения представляется собой испытания Бернулли до первого успеха.

Пример. Примерами случайных величин, имеющих геометрическое распределение, могут быть: число выстрелов до первого попадания в цель; число испытаний прибора до первого отказа; число бросаний монеты до первого выпадения орла и т.д.

Математическое ожидание и дисперсия случайной величины, подчиненной геометрическому распределению, соответственно равны $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right)/p^2$.

Пример. На пути движения рыбы к месту нереста находится $4$ шлюза. Вероятность прохода рыбы через каждый шлюз $p=3/5$. Построить ряд распределения случайной величины $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Найти $M\left(X\right),\ D\left(X\right),\ \sigma \left(X\right)$.

Пусть случайная величина $X$ — число шлюзов, пройденных рыбой до первого задержания у шлюза. Такая случайная величина подчинена геометрическому закону распределения вероятностей. Значения, которые может принимать случайная величина $X:$ 1, 2, 3, 4. Вероятности этих значений вычисляются по формуле: $P\left(X=k\right)=pq^{k-1}$, где: $p=2/5$ — вероятность задержания рыбы через шлюз, $q=1-p=3/5$ — вероятность прохода рыбы через шлюз, $k=1,\ 2,\ 3,\ 4$.

$P\left(X=1\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^0={{2}\over {5}}=0,4;$

$P\left(X=2\right)={{2}\over {5}}\cdot {{3}\over {5}}={{6}\over {25}}=0,24;$

$P\left(X=3\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^2={{2}\over {5}}\cdot {{9}\over {25}}={{18}\over {125}}=0,144;$

$P\left(X=4\right)={{2}\over {5}}\cdot {\left({{3}\over {5}}\right)}^3+{\left({{3}\over {5}}\right)}^4={{27}\over {125}}=0,216.$

Тогда ряд распределения случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end{array}$

Математическое ожидание:

$M\left(X\right)=\sum^n_{i=1}{x_ip_i}=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176.$

Дисперсия:

$D\left(X\right)=\sum^n_{i=1}{p_i{\left(x_i-M\left(X\right)\right)}^2=}0,4\cdot {\left(1-2,176\right)}^2+0,24\cdot {\left(2-2,176\right)}^2+0,144\cdot {\left(3-2,176\right)}^2+$

$+\ 0,216\cdot {\left(4-2,176\right)}^2\approx 1,377.$

Среднее квадратическое отклонение:

$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{1,377}\approx 1,173.$

4. Гипергеометрический закон распределения.

Если $N$ объектов, среди которых $m$ объектов обладают заданным свойством. Случайных образом без возвращения извлекают $n$ объектов, среди которых оказалось $k$ объектов, обладающих заданным свойством. Гипергеометрическое распределение дает возможность оценить вероятность того, что ровно $k$ объектов в выборке обладают заданным свойством. Пусть случайная величина $X$ — число объектов в выборке, обладающих заданным свойством. Тогда вероятности значений случайной величины $X$:

$P\left(X=k\right)={{C^k_mC^{n-k}_{N-m}}\over {C^n_N}}$

Замечание. Статистическая функция ГИПЕРГЕОМЕТ мастера функций $f_x$ пакета Excel дает возможность определить вероятность того, что определенное количество испытаний будет успешным.

$f_x\to $ статистические $\to $ ГИПЕРГЕОМЕТ $\to $ ОК. Появится диалоговое окно, которое нужно заполнить. В графе Число_успехов_в_выборке указываем значение $k$. Размер_выборки равен $n$. В графе Число_успехов_в_совокупности указываем значение $m$. Размер_совокупности равен $N$.

Математическое ожидание и дисперсия дискретной случайной величины $X$, подчиненной геометрическому закону распределения, соответственно равны $M\left(X\right)=nm/N$, $D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}$.

Пример. В кредитном отделе банка работают 5 специалистов с высшим финансовым образованием и 3 специалиста с высшим юридическим образованием. Руководство банка решило направить 3 специалистов Для повышения квалификации, отбирая их в случайном порядке.

а) Составьте ряд распределения числа специалистов с высшим финансовым образованием, которые могут быть направлены на повышение квалификации;

б) Найдите числовые характеристики этого распределения.

Пусть случайная величина $X$ — число специалистов с высшим финансовым образованием среди трех отобранных. Значения, которые может принимать $X:0,\ 1,\ 2,\ 3$. Данная случайная величина $X$ распределена по гипергеометрическому распределению с параметрами: $N=8$ — размер совокупности, $m=5$ — число успехов в совокупности, $n=3$ — размер выборки, $k=0,\ 1,\ 2,\ 3$ — число успехов в выборке. Тогда вероятности $P\left(X=k\right)$ можно рассчитать по формуле: $P(X=k)={C_{m}^{k} \cdot C_{N-m}^{n-k} \over C_{N}^{n} } $. Имеем:

$P\left(X=0\right)={{C^0_5\cdot C^3_3}\over {C^3_8}}={{1}\over {56}}\approx 0,018;$

$P\left(X=1\right)={{C^1_5\cdot C^2_3}\over {C^3_8}}={{15}\over {56}}\approx 0,268;$

$P\left(X=2\right)={{C^2_5\cdot C^1_3}\over {C^3_8}}={{15}\over {28}}\approx 0,536;$

$P\left(X=3\right)={{C^3_5\cdot C^0_3}\over {C^3_8}}={{5}\over {28}}\approx 0,179.$

Тогда ряд распределения случайной величины $X$:

$\begin{array}{|c|c|}
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end{array}$

Рассчитаем числовые характеристики случайной величины $X$ по общим формулам гипергеометрического распределения.

$M\left(X\right)={{nm}\over {N}}={{3\cdot 5}\over {8}}={{15}\over {8}}=1,875.$

$D\left(X\right)={{nm\left(1-{{m}\over {N}}\right)\left(1-{{n}\over {N}}\right)}\over {N-1}}={{3\cdot 5\cdot \left(1-{{5}\over {8}}\right)\cdot \left(1-{{3}\over {8}}\right)}\over {8-1}}={{225}\over {448}}\approx 0,502.$

$\sigma \left(X\right)=\sqrt{D\left(X\right)}=\sqrt{0,502}\approx 0,7085.$

Дискретные двумерные случайные величины. Пример решения задачи на Викиматик

Довольно часто при изучении случайных величин приходится иметь дело с двумя, тремя и даже большим числом случайных величин. Например, двумерной случайной величиной $\left(X,\ Y\right)$ будет описываться точка попадания снаряда, где случайные величины $X,\ Y$ абсцисса и ордината соответственно. Успеваемость наудачу взятого студента в период сессии характеризуется $n$-мерной случайной величиной $\left(X_1,\ X_2,\ \dots ,\ X_n\right)$, где случайные величины $X_1,\ X_2,\ \dots ,\ X_n$ — это оценки, проставленные в зачетной книжке по различным дисциплинам.

Набор $n$ случайных величин $\left(X_1,\ X_2,\ \dots ,\ X_n\right)$ называется случайным вектором. Мы ограничимся рассмотрением случая $\left(X,\ Y\right)$.

Пусть $X$ — дискретная случайная величина с возможными значениями $x_1,x_2,\ \dots ,\ x_n$, а $Y$ — дискретная случайная величина с возможными значениями $y_1,y_2,\ \dots ,\ y_n$.

Тогда дискретная двумерная случайная величина $\left(X,\ Y\right)$ может принимать значения $\left(x_i,\ y_j\right)$ с вероятностями $p_{ij}=P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)=P\left(X=x_i\right)P\left(Y=y_j|X=x_i\right)$. Здесь $P\left(Y=y_j|X=x_i\right)$ — это условная вероятность того, что случайная величина $Y$ примет значение $y_j$ при условии, что случайная величина $X$ приняла значение $x_i$.

Вероятность того, что случайная величина $X$ примет значение $x_i$, равна $p_i=\sum_j{p_{ij}}$. Вероятность того, что случайная величина $Y$ примет значение $y_j$, равна $q_j=\sum_i{p_{ij}}$.

Если считать, что событие $Y=y_j$ произошло, то распределение случайной величины $X$ при условии $Y=y_j$ называется условным распределением случайной величины $X$ при условии $Y=y_j$. Тогда:

$$P\left(X=x_i|Y=y_j\right)={{P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)}\over {P\left(Y=y_j\right)}}={{p_{ij}}\over {q_j}}.$$

Если считать, что событие $X=x_i$ произошло, то распределение случайной величины $Y$ при условии $X=x_i$ называется условным распределением случайной величины $Y$ при условии $X=x_i$. Тогда:

$$P\left(Y=y_j|X=x_i\right)={{P\left(\left(X=x_i\right)\left(Y=y_j\right)\right)}\over {P\left(X=x_i\right)}}={{p_{ij}}\over {p_i}}.$$

Пример 1. Задано распределение двумерной случайной величины:

$\begin{array}{|c|c|}
\hline
X\backslash Y & 2 & 3 \\
\hline
-1 & 0,15 & 0,25 \\
\hline
0 & 0,28 & 0,13 \\
\hline
1 & 0,09 & 0,1 \\
\hline
\end{array}$

Определим законы распределения случайных величин $X$ и $Y$. Найдем условные распределения случайной величины $X$ при условии $Y=2$ и случайной величины $Y$ при условии $X=0$.

Заполним следующую таблицу:

$\begin{array}{|c|c|}
\hline
X\backslash Y & 2 & 3 & p_i & p_{ij}/q_1 \\
\hline
-1 & 0,15 & 0,25 & 0,4 & 0,29 \\
\hline
0 & 0,28 & 0,13 & 0,41 & 0,54 \\
\hline

1 & 0,09 & 0,1 & 0,19 & 0,17 \\
\hline
q_j & 0,52 & 0,48 & 1 & \\
\hline
p_{ij}/p_2 & 0,68 & 0,32 & & \\
\hline
1 & 0,09 & 0,1 \\
\hline
\end{array}$

Поясним, как заполняется таблица. Значения первых трех столбцов первых четырех строк взяты из условия. Сумму чисел $2$-го и $3$-го столбцов $2$-й ($3$-й) строки укажем в $4$-м столбце $2$-й ($3$-й) строки. Сумму чисел $2$-го и $3$-го столбцов $4$-й строки укажем в $4$-м столбце $4$-й строки.

Сумму чисел $2$-й, $3$-й и $4$-й строк $2$-го ($3$-го) столбца запишем в $5$-й строке $2$-го ($3$-го) столбца. Каждое число $2$-го столбца делим на $q_1=0,52$, результат округляем до двух цифр после запятой и пишем в $5$-м столбце. Числа из $2$-го и $3$-го столбцов $3$-й строки делим на $p_2=0,41$, результат округляем до двух цифр после запятой и пишем в последней строке.

Тогда закон распределения случайной величины $X$ имеет следующий вид.

$\begin{array}{|c|c|}
\hline
X & -1 & 0 & 1 \\
\hline
p_i & 0,4 & 0,41 & 0,19 \\
\hline
\end{array}$

Закон распределения случайной величины $Y$.

$\begin{array}{|c|c|}
\hline
Y & 2 & 3 \\
\hline
q_j & 0,52 & 0,48 \\
\hline
\end{array}$

Условное распределение случайной величины $X$ при условии $Y=2$ имеет следующий вид.

$\begin{array}{|c|c|}
\hline
X & -1 & 0 & 1 \\
\hline
p_{ij}/q_1 & 0,29 & 0,54 & 0,17 \\
\hline
\end{array}$

Условное распределение случайной величины $Y$ при условии $X=0$ имеет следующий вид.

$\begin{array}{|c|c|}
\hline
Y & 2 & 3 \\
\hline
p_{ij}/p_2 & 0,68 & 0,32 \\
\hline
\end{array}$

Пример 2. Имеем шесть карандашей, среди которых два красных. Раскладываем карандаши в две коробки. В первую кладут $2$ штуки, а во вторую тоже два. $X$ — количество красных карандашей в первой коробке, a $Y$ — во второй. Написать закон распределения системы случайных величин $(X,\ Y)$.

Пусть дискретная случайная величина $X$ — количество красных карандашей в первой коробке, а дискретная случайная величина $Y$ — количество красных карандашей во второй коробке. Возможные значения случайных величин $X,\ Y$ соответственно $X:0,\ 1,\ 2$, $Y:0,\ 1,\ 2$. Тогда дискретная двумерная случайная величина $\left(X,\ Y\right)$ может принимать значения $\left(x,\ y\right)$ с вероятностями $P=P\left(\left(X=x\right)\times \left(Y=y\right)\right)=P\left(X=x\right)\times P\left(Y=y|X=x\right)$, где $P\left(Y=y|X=x\right)$ — условная вероятность того, что случайная величина $Y$ примет значение $y$ при условии, что случайная величина $X$ приняла значение $x$. Изобразим соответствие между значениями $\left(x,\ y\right)$ и вероятностями $P\left(\left(X=x\right)\times \left(Y=y\right)\right)$ в виде следующей таблицы.

$\begin{array}{|c|c|}
\hline
X\backslash Y & 0 & 1 & 2 \\
\hline
0 & {{1}\over {15}} & {{4}\over {15}} & {{1}\over {15}} \\
\hline
1 & {{4}\over {15}} & {{4}\over {15}} & 0 \\
\hline
2 & {{1}\over {15}} & 0 & 0 \\
\hline
\end{array}$

По строкам такой таблицы указываются значения $X$, а по столбцам значения $Y$, тогда вероятности $P\left(\left(X=x\right)\times \left(Y=y\right)\right)$ указываются на пересечении соответствующей строки и столбца. Рассчитаем вероятности, используя классическое определение вероятности и теорему произведения вероятностей зависимых событий.

$$P\left(\left(X=0\right)\left(Y=0\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^2_2}\over {C^2_4}}={{6}\over {15}}\cdot {{1}\over {6}}={{1}\over {15}};$$

$$P\left(\left(X=0\right)\left(Y=1\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^1_2\cdot C^1_2}\over {C^2_4}}={{6}\over {15}}\cdot {{2\cdot 2}\over {6}}={{4}\over {15}};$$

$$P\left(\left(X=0\right)\left(Y=2\right)\right)={{C^2_4}\over {C^2_6}}\cdot {{C^2_2}\over {C^2_4}}={{6}\over {15}}\cdot {{1}\over {6}}={{1}\over {15}};$$

$$P\left(\left(X=1\right)\left(Y=0\right)\right)={{C^1_2\cdot C^1_4}\over {C^2_6}}\cdot {{C^2_3}\over {C^2_4}}={{2\cdot 4}\over {15}}\cdot {{3}\over {6}}={{4}\over {15}};$$

$$P\left(\left(X=1\right)\left(Y=1\right)\right)={{C^1_2\cdot C^1_4}\over {C^2_6}}\cdot {{C^1_1\cdot C^1_3}\over {C^2_4}}={{2\cdot 4}\over {15}}\cdot {{1\cdot 3}\over {6}}={{4}\over {15}};$$

$$P\left(\left(X=2\right)\left(Y=0\right)\right)={{C^2_2}\over {C^2_6}}\cdot {{C^2_4}\over {C^2_4}}={{1}\over {15}}\cdot 1={{1}\over {15}}.$$

Поскольку в законе распределения (полученной таблице) все множество событий образует полную группу событий, то сумма вероятностей должна быть равна 1. Проверим это:

$$\sum_{i,\ j}{p_{ij}}={{1}\over {15}}+{{4}\over {15}}+{{1}\over {15}}+{{4}\over {15}}+{{4}\over {15}}+{{1}\over {15}}=1.$$

Функция распределения двумерной случайной величины

Функцией распределения двумерной случайной величины $\left(X,\ Y\right)$ называется функция $F\left(x,\ y\right)$, которая для любых действительных чисел $x$ и $y$ равна вероятности совместного выполнения двух событий $\left\{X < x\right\}$ и $\left\{Y < y\right\}$. Таким образом, по определению

$$F\left(x,\ y\right)=P\left\{X < x,\ Y < y\right\}.$$

Для дискретной двумерной случайной величины функция распределения находится путем суммирования всех вероятностей $p_{ij}$, для которых $x_i < x,\ y_j < y$, то есть

$$F\left(x,\ y\right)=\sum_{x_i < x}{\sum_{y_j < y}{p_{ij}}}.$$

Свойства функции распределения двумерной случайной величины.

1. Функция распределения $F\left(x,\ y\right)$ является ограниченной, то есть $0\le F\left(x,\ y\right)\le 1$.

2. $F\left(x,\ y\right)$ не убывающая для каждого из своих аргументов при фиксированном другом, то есть $F\left(x_2,\ y\right)\ge F\left(x_1,\ y\right)$ при $x_2>x_1$, $F\left(x,\ y_2\right)\ge F\left(x,\ y_1\right)$ при $y_2>y_1$.

3. Если хотя бы один из аргументов принимает значение $-\infty $, то функция распределения будет равна нулю, то есть $F\left(-\infty ,\ y\right)=F\left(x,\ -\infty \right),\ F\left(-\infty ,\ -\infty \right)=0$.

4. Если оба аргумента принимают значение $+\infty $, то функция распределения будет равна $1$, то есть $F\left(+\infty ,\ +\infty \right)=1$.

5. В том случае, когда ровно один из аргументов принимает значение $+\infty $, функция распределения $F\left(x,\ y\right)$ становится функцией распределения случайной величины, соответствующей другому элементу, то есть $F\left(x,\ +\infty \right)=F_1\left(x\right)=F_X\left(x\right),\ F\left(+\infty ,\ y\right)=F_y\left(y\right)=F_Y\left(y\right)$.

6. $F\left(x,\ y\right)$ является непрерывной слева для каждого из своих аргументов, то есть

$${\mathop{lim}_{x\to x_0-0} F\left(x,\ y\right)\ }=F\left(x_0,\ y\right),\ {\mathop{lim}_{y\to y_0-0} F\left(x,\ y\right)\ }=F\left(x,\ y_0\right).$$

Пример 3. Пусть дискретная двумерная случайная величина $\left(X,\ Y\right)$ задана рядом распределения.

$\begin{array}{|c|c|}
\hline
X\backslash Y & 0 & 1 \\
\hline
0 & {{1}\over {6}} & {{2}\over {6}} \\
\hline
1 & {{2}\over {6}} & {{1}\over {6}} \\
\hline
\end{array}$

Тогда функция распределения:

$F(x,y)=\left\{\begin{matrix}
0,\ при\ x\le 0,\ y\le 0 \\
0,\ при\ x\le 0,\ 0 < y\le 1 \\
0,\ при\ x\le 0,\ y>1 \\
0,\ при\ 0 < x\le 1,\ y\le 0 \\
{{1}\over {6}},\ при\ 0 < x\le 1,\ 0 < y\le 1 \\
{{1}\over {6}}+{{2}\over {6}}={{1}\over {2}},\ при\ 0 < x\le 1,\ y>1 \\
0,\ при\ x>1,\ y\le 0 \\
{{1}\over {6}}+{{2}\over {6}}={{1}\over {2}},\ при\ x>1,\ 0 < y\le 1 \\
{{1}\over {6}}+{{2}\over {6}}+{{2}\over {6}}+{{1}\over {6}}=1,\ при\ x>1,\ y>1 \\
\end{matrix}\right.$

Дискретная случайная величина и ее числовые характеристики. Примеры решения задач

Дискретная случайная величина и ее числовые характеристики

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
Закон распределения
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Функцией распределения дискретной случайной величины называют функцию:
,
определяющую для каждого значения аргумента x вероятность того, что случайная величина X примет значение, меньшее этого x.

Математическое ожидание дискретной случайной величины
,
где — значение дискретной случайной величины; — вероятности принятия случайной величиной X значений .
Если случайная величина принимает счетное множество возможных значений, то:
.
Математическое ожидание числа наступлений события в n независимых испытаниях:
,
где p — вероятность наступления события.
Дисперсия и среднеквадратическое отклонение дискретной случайной величины
Дисперсия дискретной случайной величины:
или .
Дисперсия числа наступлений события в n независимых испытаниях
,
где p — вероятность наступления события.
Среднеквадратическое отклонение дискретной случайной величины:
.

Пример 1
Составьте закон распределения вероятностей дискретной  случайной величины (д.с.в.) X – числа k выпадений  хотя бы одной «шестерки» в n = 8  бросаниях пары игральных кубиков. Постройте многоугольник распределения. Найдите  числовые характеристики распределения (моду распределения, математическое  ожидание M(X), дисперсию D(X), среднее квадратическое отклонение s(X)).

Решение: Введем обозначение: событие A – «при бросании пары игральных кубиков шестерка появилась хотя бы один раз». Для нахождения вероятности P(A) = p события A удобнее вначале найти вероятность P(Ā) = q противоположного события Ā – «при бросании пары игральных кубиков шестерка не появилась ни разу».
Поскольку вероятность непоявления «шестерки» при бросании одного кубика равна 5/6, то по теореме умножения вероятностей
P(Ā) = q = = .
Соответственно,
P(A) = p = 1 – P(Ā) = .
Испытания в задаче проходят по схеме Бернулли, поэтому д.с.в. величина X – число k выпадений хотя одной шестерки при бросании двух кубиков подчиняется биномиальному закону распределения вероятностей:

где = – число сочетаний из n по k.

Проведенные для данной задачи расчеты удобно оформить в виде таблицы:
Распределение вероятностей д.с.в. X º k (n = 8; p = ; q = )

k	0	1	2	3	4	5	6	7	8	Сумма
	1	8	28	56	70	56	28	8	1
Pn(k)	0,0541	0,1904	0,2932	0,258	0,1419	0,05	0,011	0,0013	0,0001	1

Полигон (многоугольник) распределения вероятностей дискретной случайной величины X представлен на рис.:

Рис. Полигон распределения вероятностей д.с.в. X=k.
Вертикальной линией показано математическое ожидание распределения M(X).

Найдем числовые характеристики распределения вероятностей д.с.в. X. Мода распределения равна 2 (здесь P8(2) = 0,2932 максимально). Математическое ожидание по определению равно:
M(X) = = 2,4444,
где xk = k – значение, принимаемое д.с.в. X. Дисперсию D(X) распределения найдем по формуле:
D(X) = = 4,8097.
Среднее квадратическое отклонение (СКО):
s(X) = = 2,1931.


 Пример2
Дискретная случайная величинаX задана законом  распределения  
 Найти функцию распределения F(x) и построить ее график.

Решение. Если , то (третье свойство).
Если , то . Действительно, X может принять значение 1 с вероятностью 0,3.
Если , то . Действительно, если удовлетворяет неравенству
, то равно вероятности события , которое может быть осуществлено, когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события равна сумме вероятностей 0,3 + 0,1=0,4. Если , то . Действительно, событие достоверно, следовательно, его вероятность равна единице. Итак, функция распределения аналитически может быть записана так:

График этой функции:

Пример3
В магазине куплено 3 электроприбора: чайник, утюг и  пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого  из них соответственно равны   . Составить закон распределения случайной величины  X – числа приборов, вышедших из строя в течение гарантийного  срока.

Решение. X – число приборов, вышедших из строя, имеет следующие возможные значения:
— все три прибора не выйдут из строя в течении гарантийного срока;
— один прибор выйдет из строя;
— два прибора выйдут из строя;
— три прибора выйдут из строя.
Найдем соответствующие этим значениям вероятности. По условию, вероятности выхода из строя приборов равны: тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны:

Закон распределения имеет вид:

	0	1	2	3
	0,684	0,283	0,032	0,001

Проверка: 1.

Числовые характеристики дискретной случайной величины

Числовые характеристики дискретной случайной величины.

Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение.

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:

$\sum_{i=1}^n x_{i} \cdot p_{i}=x_{1} \cdot p_{1}+x_{2} \cdot p_{2}+\cdots +x_{n} \cdot p_{n}$

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной:

$M(C)=C$

2. Постоянную можно выносить за знак математического ожидания:

$M(CX)=CM(X)$

3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:

$M(X_1 \cdot X_2 \cdot ... \cdot X_n)=M(X_1)\cdot M(X_2)\cdot ... \cdot M(X_n)$

4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:

$M(X_1 + X_2 + ... + X_n)=M(X_1) + M(X_2) + ... + M(X_n)$

(для разности аналогично)

Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

$D(X)=M{[X-M(X)]}^2$

Дисперсию удобно вычислять по формуле:

$D(X)=M(X^2)-{[M(X)]}^2$

Свойства дисперсии:

1. Дисперсия постоянной равна нулю:

$D(C)=0$

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

$D(CX)=C^2D(X)$

3. Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых:

$D(X_1 \pm X_2 \pm ... \pm X_n)=D(X_1) + D(X_2) + ... + D(X_n)$

$D(X+C)=D(X)$

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

$\sigma (X) =\sqrt{D(X)}$

Рассмотрим следующие задачи.

1. Математическое ожидание и дисперсия СВ Х соответственно равны 0,5 и 5. Найти математическое ожидание и дисперсию случайной величины 2X-3 .

Решение.

Согласно свойствам математического ожидания и дисперсии, получаем:

$M(2X-3)=M(2X)+M(-3)=2M(X)-3=2\cdot \frac12-3=1-3=-2$

$D(2X-3)=4\cdot D(X)=4\cdot 5=20$

2. Случайные величины X и Y независимы, причем D(X)=3 и D(Y)=5 . Найти D(Z) , если $Z=4\cdot X- 5 \cdot Y +3$ .

Решение.

На основании свойств дисперсии получаем:

$D(Z)=D(4\cdot X- 5 \cdot Y +3)=16\cdot D(X)+25\cdot D(Y)=16\cdot 3+25\cdot 5=48+125=173$

3. Закон распределения ДСВ Х задан таблицей распределения

Найти: $c,\quad M(X), \quad D(X), \quad \sigma (X), \quad P\{X<3\}.$

1) Так как $\sum_{i=1}^4 p_i =1$ , т.е. $\frac18 +\frac14 +\frac13+c=1$ , следовательно

$c=1-\frac18 -\frac14 -\frac13=\frac{24-3-6-8}{24}=\frac{7}{24}$

Т.о. закон распределения примет вид

$M(X)=\sum_{i=1}^4 x_i \cdot p_i=1\cdot \frac18+2\cdot \frac14+3\cdot \frac13+4\cdot \frac{7}{24}=\frac18+\frac12+1+\frac76=$

$=\frac{3+12+24+28}{24}=\frac{67}{24};$

2) Для вычисления дисперсии воспользуемся формулой:

$D(X)=M(X^2)-{[M(X)]}^2$

Сначала найдем математическое ожидание ДСВ Х2 для этого составим закон распределения этой СВ. Напоминаю, что для этого необходимо каждое значение ДСВ Х возвести в квадрат, а вероятности оставляем прежними. При одинаковых значениях ДСВ вероятности складываем.

$M(X^2)=1\cdot \frac18+4\cdot \frac14+9\cdot \frac13+16\cdot \frac{7}{24}=\frac18+1+3+\frac{14}{3}=\frac{3+96+112}{24}=\frac{211}{24};$

$D(X)=\frac{211}{24}-{\left(\frac{67}{24}\right)}^2=\frac{24\cdot 211-{67}^2}{{24}^2}=\frac{5064-4489}{576}=\frac{575}{576};$

3) Найдем среднее квадратическое отклонение:

$\sigma (X) =\sqrt{D(X)}=\sqrt{\frac{575}{576}}=\frac{5\sqrt{23}}{24}$

$P\{X<3\}=P\{X=1\}+P\{X=2\}=\frac18+\frac14=\frac38$

4. Функция распределения ДСВ Х имеет вид

$F(x)=\{ 0, \qquad \qquad x\le 0 \\ 0,2, \qquad 0< x \le 1, \\ 0,6, \qquad \qquad 1< x \le 2 \\ 0,9, \qquad \qquad 2< x \le 3 \\ 1, \qquad \qquad x>3$

Найти:

$M(X), \quad M(X^2) \quad D(X), \quad \sigma (X).$

Решение.

Составляем закон распределения ДСВ Х (т.е. выполняем операцию обратную той, которую мы делали в предыдущей статье)

	0	1	2	3
	0,2	0,4	0,3	0,1

$M(X)=0\cdot 0,2+1\cdot 0,4+2\cdot 0,3+3\cdot 0,1=0,4+0,6+0,3=1,3$

Составляем закон распределения ДСВ X^2

	0	1	4	9
	0,2	0,4	0,3	0,1

$M(X^2)=0\cdot 0,2+1\cdot 0,4+4\cdot 0,3+9\cdot 0,1=0,4+1,2+0,9=2,5$

$D(X)=M(X^2)-{[M(X)]}^2=2,5-{1,3}^2=2,5-1,69=0,81$

$\sigma (X)=\sqrt{0,81}=0,9$

5. Независимые случайные величины X и Y заданы таблицами распределения вероятностей

	10	20
	0,2	0,8

	30	40	50
	0,5	0,3	0,2

Найти D(X+Y) двумя способами:

1. Составив предварительно таблицу распределения СВ Z=X+Y ;

2. Используя правило сложения дисперсий.

Решение.

Составим таблицу распределения ДСВ Z=X+Y .

Найдем $z_{ij}=x_i+y_{j}$

10+30=40 20+30=50
10+40=50 20+40=60
10+50=60 20+50=70
Т.о. значения ДСВ Z таковы: $z_1=40,\quad z_2=50,\quad z_3=60,\quad z_4=70$

Найдем соответствующие им вероятности:

$p_1=P\{Z=40\}=P\{X=10, Y=30\}=0,2\cdot 0,5=0,1$

$p_2=P\{Z=50\}=P\{X=10, Y=40\}+P\{X=20, Y=30\}=$

$=0,2\cdot 0,3+0,8\cdot 0,5=0,06+0,4=0,46$

$p_3=P\{Z=60\}=P\{X=10, Y=50\}+P\{X=20, Y=40\}=$

$=0,2\cdot 0,2+0,8\cdot 0,3=0,04+0,24=0,28$

$p_4=P\{Z=70\}=P\{X=20, Y=50\}=0,8\cdot 0,2=0,16$

Получаем ряд распределения СВ Z

	40	50	60	70
	0,1	0,46	0,28	0,16

$M(Z)=\sum_{i=1}^4 z_i \cdot p_i=40\cdot 0,1+50\cdot 0,46+60\cdot 0,28+70\cdot 0,16=4+23+16,8+11,2=55;$

$M(Z^2)=\sum_{i=1}^4 z_i^2 \cdot p_i=1600\cdot 0,1+2500\cdot 0,46+3600\cdot 0,28+4900\cdot 0,16=$

$=160+1150+1008+784=3102;$

$D(Z)=M(Z^2)-{[M(Z)]}^2=3102-3025=77$

2. Используя правило сложения дисперсий:

$D(Z)=D(X+Y)=D(X)+D(Y)$

$D(X)=M(X^2)-{[M(X)]}^2$

$M(X)=10\cdot 0,2+20\cdot 0,8=2+16=18;$

$M(X^2)=100\cdot 0,2+400\cdot 0,8=20+320=340;$

$M(Y)=30\cdot 0,5+40\cdot 0,3+50\cdot 0,2=15+12+10=37$

$M(Y^2)=900\cdot 0,5+1600\cdot 0,3+2500\cdot 0,2=450+480+500=1430$

$D(Y)=1430-1369=61$

$D(Z)=16+61=77$

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ — КиберПедия

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется переменная, которая в результате испытания принимает одно и только одно возможное значение, но какое именно – заранее не известно.

Примеры случайных величин:

— количество студентов на лекции;

— количество больных в городе;

— число родившихся в течение суток в г. Кемерово;

— продолжительность человеческой жизни.

Случайные величины принято обозначать прописными латинскими буквами X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z,…

Вероятности случайных величин обозначают буквами с соответствующими индексами — запись показывает вероятность того, что случайная величина принимает значение .

Случайные величины разделяют на дискретные и непрерывные.

Дискретной называют случайную величину, принимающую отдельные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.

Например,

— количество мальчиков, родившихся в каком-либо месяце;

— количество рецептов, поступивших в аптеку в течение дня;

— число ударов пульса больного в минуту;

— количество осложнений после операций в данной больнице.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Число возможных значений непрерывной случайной величины бесконечно.

Например,

— температура воздуха в течение дня;

— продолжительность человеческой жизни;

— время инкубационного периода заболевания.

ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ПЛОТНОСТЬ ВЕРОЯТНОСТИ

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.

Для непрерывной случайной величины можно дать еще одно определение:

Случайная величина называется непрерывной, если ее функция распределения непрерывно в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Непрерывную случайную величину можно задать не только с помощью функции распределения , но и с помощью плотности вероятности.

Плотностью вероятности (плотностью распределения) непрерывной случайной величины называется производная ее функции распределения

Иногда функцию называют дифференциальной функцией распределения или дифференциальным законом распределения.

График плотности вероятности называют кривой распределения. Кривая распределения лежит не ниже оси абсцисс, и площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Свойства плотности вероятности непрерывной случайной величины

1. Плотность вероятности – неотрицательная функция

2. Вероятность попадания непрерывной случайной величины в интервал равна определенному интегралу от ее плотности вероятности в пределах от до

3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Примеры случайных величин:

— количество студентов на лекции;

— количество больных в городе;

— число родившихся в течение суток в г. Кемерово;

— продолжительность человеческой жизни.

Случайные величины разделяют на дискретные и непрерывные.

Например,

— количество мальчиков, родившихся в каком-либо месяце;

— количество рецептов, поступивших в аптеку в течение дня;

— число ударов пульса больного в минуту;

— количество осложнений после операций в данной больнице.

Например,

— температура воздуха в течение дня;

— продолжительность человеческой жизни;

— время инкубационного периода заболевания.

Дискретная случайная величина. Закон распределения дискретной случайной величины. Числовые характеристики дискретных случайных величин. — Студопедия

Случайной величинойназывается величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.

Случайные величины можно разделить на две категории.

Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).

Это множество может быть как конечным, так и бесконечным.

Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.

Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.

Очевидно, что число возможных значений непрерывной случайной величины бесконечно.

Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.

Закон распределения полностью характеризует случайную величину. Однако, когда невозможно найти закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины. Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

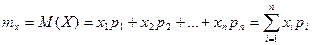
Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно.

С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания.

1) Математическое ожидание постоянной величины равно самой постоянной.

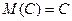
2) Постоянный множитель можно выносить за знак математического ожидания.

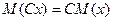
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

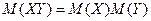
Это свойство справедливо для произвольного числа случайных величин.

4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

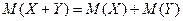
Это свойство также справедливо для произвольного числа случайных величин.

Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

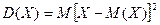
Вычисление дисперсии.

Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания.

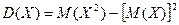
Свойства дисперсии.

1) Дисперсия постоянной величины равна нулю.

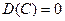
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

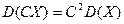
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

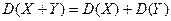
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

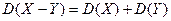
Справедливость этого равенства вытекает из свойства 2.

Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии.

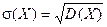
Функция распределения.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

Функцию распределения также называют интегральной функцией.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет вид:

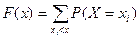
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение х_i.

Свойства функции распределения..

1) значения функции распределения принадлежат отрезку [0, 1].

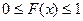
2) F(x) – неубывающая функция.

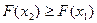при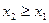

3) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале.

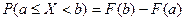
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

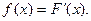
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

90000 Discrete Random Variables — Mathematics A-Level Revision 90001 90002 This section covers Discrete Random Variables, probability distribution, Cumulative Distribution Function and Probability Density Function. 90003 90002 A 90005 probability distribution 90006 is a table of values showing the probabilities of various outcomes of an experiment. 90003 90002 For example, if a coin is tossed three times, the number of heads obtained can be 0, 1, 2 or 3. The probabilities of each of these possibilities can be tabulated as shown: 90003 90010 90011 90012 90013 90002 Number of Heads 90003 90016 90013 90002 0 90003 90016 90013 90002 1 90003 90016 90013 90002 2 90003 90016 90013 90002 3 90003 90016 90033 90012 90013 90002 Probability 90003 90016 90013 90002 1/8 90003 90016 90013 90002 3/8 90003 90016 90013 90002 3/8 90003 90016 90013 90002 1/8 90003 90016 90033 90056 90057 90002 A 90005 discrete variable 90006 is a variable which can only take a countable number of values.In this example, the number of heads can only take 4 values (0, 1, 2, 3) and so the variable is discrete. The variable is said to be 90005 random 90006 if the sum of the probabilities is one. 90003 90002 90065 90005 Probability Density Function 90006 90068 90003 90002 The probability density function (p.d.f.) of X (or probability mass function) is a function which allocates probabilities. Put simply, it is a function which tells you the probability of certain events occurring. The usual notation that is used is P (X = x) = something.The random variable (r.v.) X is the event that we are considering. So in the above example, X represents the number of heads that we throw. So P (X = 0) means «the probability that no heads are thrown». Here, P (X = 0) = 1/8 (the probability that we throw no heads is 1/8). 90003 90002 In the above example, we could therefore have written: 90003 90010 90011 90012 90013 90002 x 90003 90016 90013 90002 0 90003 90016 90013 90002 1 90003 90016 90013 90002 2 90003 90016 90013 90002 3 90003 90016 90033 90012 90013 90002 P (X = x) 90003 90016 90013 90002 1/8 90003 90016 90013 90002 3/8 90003 90016 90013 90002 3/8 90003 90016 90013 90002 1/8 90003 90016 90033 90056 90057 90002 Quite often, the probability density function will be given to you in terms of x.In the above example, P (X = x) = 90123 3 90124 C 90125 x 90126 / (2) 90123 3 90124 (see permutations and combinations for the meaning of 90123 3 90124 C 90125 x 90126). 90003 90002 90135 90005 Example 90006 90138 90003 90002 A die is thrown repeatedly until a 6 is obtained. Find the probability density function for the number times we throw the die. 90003 90002 Let X be the random variable representing the number of times we throw the die. 90003 90002 P (X = 1) = 1/6 (if we only throw the die once, we get a 6 on our first throw.The probability of this is 1/6). 90003 90002 P (X = 2) = (5/6) × (1/6) (if we throw the die twice before getting a 6, we must throw something that is not a 6 with our first throw, the probability of which is 5/6 and we must throw a 6 on our second throw, the probability of which is 1/6) 90003 90002 etc 90003 90002 In general, P (X = x) = (5/6) 90123 (x-1) 90124 × (1/6) 90003 90002 90065 90005 Cumulative Distribution Function 90006 90068 90003 90002 The cumulative distribution function (c.d.f.) of a discrete random variable X is the function F (t) which tells you the probability that X is less than or equal to t. So if X has p.d.f. P (X = x), we have: 90003 90002 F (t) = P (X £ t) = SP (X = x). 90003 90002 In other words, for each value that X can be which is less than or equal to t, work out the probability that X is that value and add up all such results. 90003 90002 90135 90005 Example 90006 90138 90003 90002 In the above example where the die is thrown repeatedly, lets work out P (X £ t) for some values of t.90003 90002 P (X £ 1) is the probability that the number of throws until we get a 6 is less than or equal to 1. So it is either 0 or 1. 90003 90002 P (X = 0) = 0 and P (X = 1) = 1/6. Hence P (X £ 1) = 1/6 90003 90002 Similarly, P (X £ 2) = P (X = 0) + P (X = 1) + P (X = 2) = 0 + 1/6 + 5/36 = 11/36 90003 .90000 Discrete Random Variables 90001 90002 It is often the case that a number is naturally associated to the outcome of a random experiment: the number of boys in a three-child family, the number of defective light bulbs in a case of 100 bulbs, the length of time until the next customer arrives at the drive-through window at a bank. Such a number varies from trial to trial of the corresponding experiment, and does so in a way that can not be predicted with certainty; hence, it is called a 90003 random variable 90004.In this chapter and the next we study such variables. 90005 90006 4.1 Random Variables 90007 90008 Learning Objectives 90009 90010 90011 To learn the concept of a random variable. 90012 90011 To learn the distinction between discrete and continuous random variables. 90012 90015 90008 Definition 90009 90002 90003 A 90004 random variableA numerical value generated by a random experiment. 90003 is a numerical quantity that is generated by a random experiment.90004 90005 90002 We will denote random variables by capital letters, such as 90003 X 90004 or 90003 Z 90004, and the actual values that they can take by lowercase letters, such as 90003 x 90004 and 90003 z 90004. 90005 90002 Table 4.1 «Four Random Variables» gives four examples of random variables. In the second example, the three dots indicates that every counting number is a possible value for 90003 X 90004. Although it is highly unlikely, for example, that it would take 50 tosses of the coin to observe heads for the first time, nevertheless it is conceivable, hence the number 50 is a possible value.The set of possible values is infinite, but is still at least 90003 countable 90004, in the sense that all possible values can be listed one after another. In the last two examples, by way of contrast, the possible values can not be individually listed, but take up a whole interval of numbers. In the fourth example, since the light bulb could conceivably continue to shine indefinitely, there is no natural greatest value for its lifetime, so we simply place the symbol ∞ for infinity as the right endpoint of the interval of possible values.90005 90002 Table 4.1 Four Random Variables 90005 90042 90043 90044 90045 Experiment 90046 90045 Number 90003 X 90004 90046 90045 Possible Values of 90003 X 90004 90046 90055 90056 90057 90044 90059 Roll two fair dice 90060 90059 Sum of the number of dots on the top faces 90060 90059 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 90060 90055 90044 90059 Flip a fair coin repeatedly 90060 90059 Number of tosses until the coin lands heads 90060 90059 1, 2, 3,4, … 90060 90055 90044 90059 Measure the voltage at an electrical outlet 90060 90059 Voltage measured 90060 90059 118 ≤ 90003 x 90004 ≤ 122 90060 90055 90044 90059 Operate a light bulb until it burns out 90060 90059 Time until the bulb burns out 90060 90059 0 ≤ 90003 x 90004 <∞ 90060 90055 90094 90095 90008 Definition 90009 90002 90003 A random variable is called 90004 discreteA random variable with a finite or countable number of possible values.90003 if it has either a finite or a countable number of possible values. A random variable is called 90004 continuousA random variable whose possible values contain an interval of decimal numbers. 90003 if its possible values contain a whole interval of numbers. 90004 90005 90002 The examples in the table are typical in that discrete random variables typically arise from a counting process, whereas continuous random variables typically arise from a measurement. 90005 90008 Key Takeaways 90009 90110 90011 A random variable is a number generated by a random experiment.90012 90011 A random variable is called 90003 discrete 90004 if its possible values form a finite or countable set. 90012 90011 A random variable is called 90003 continuous 90004 if its possible values contain a whole interval of numbers. 90012 90121 90008 Exercises 90009 90124 90008 Basic 90009 90011 90002 Classify each random variable as either discrete or continuous.90005 90130 90011 The number of arrivals at an emergency room between midnight and 6:00 a.m. 90012 90011 The weight of a box of cereal labeled "18 ounces." 90012 90011 The duration of the next outgoing telephone call from a business office. 90012 90011 The number of kernels of popcorn in a 1-pound container. 90012 90011 The number of applicants for a job.90012 90015 90012 90011 90002 Classify each random variable as either discrete or continuous. 90005 90130 90011 The time between customers entering a checkout lane at a retail store. 90012 90011 The weight of refuse on a truck arriving at a landfill. 90012 90011 The number of passengers in a passenger vehicle on a highway at rush hour.90012 90011 The number of clerical errors on a medical chart. 90012 90011 The number of accident-free days in one month at a factory. 90012 90015 90012 90011 90002 Classify each random variable as either discrete or continuous. 90005 90130 90011 The number of boys in a randomly selected three-child family.90012 90011 The temperature of a cup of coffee served at a restaurant. 90012 90011 The number of no-shows for every 100 reservations made with a commercial airline. 90012 90011 The number of vehicles owned by a randomly selected household. 90012 90011 The average amount spent on electricity each July by a randomly selected household in a certain state. 90012 90015 90012 90011 90002 Classify each random variable as either discrete or continuous.90005 90130 90011 The number of patrons arriving at a restaurant between 5:00 p.m. and 6:00 p.m. 90012 90011 The number of new cases of influenza in a particular county in a coming month. 90012 90011 The air pressure of a tire on an automobile. 90012 90011 The amount of rain recorded at an airport one day. 90012 90011 The number of students who actually register for classes at a university next semester.90012 90015 90012 90011 90002 Identify the set of possible values for each random variable. (Make a reasonable estimate based on experience, where necessary.) 90005 90130 90011 The number of heads in two tosses of a coin. 90012 90011 The average weight of newborn babies born in a particular county one month. 90012 90011 The amount of liquid in a 12-ounce can of soft drink.90012 90011 The number of games in the next World Series (best of up to seven games). 90012 90011 The number of coins that match when three coins are tossed at once. 90012 90015 90012 90011 90002 Identify the set of possible values for each random variable. (Make a reasonable estimate based on experience, where necessary.) 90005 90130 90011 The number of hearts in a five-card hand drawn from a deck of 52 cards that contains 13 hearts in all.90012 90011 The number of pitches made by a starting pitcher in a major league baseball game. 90012 90011 The number of breakdowns of city buses in a large city in one week. 90012 90011 The distance a rental car rented on a daily rate is driven each day. 90012 90011 The amount of rainfall at an airport next month. 90012 90015 90012 90015 90008 Answers 90009 90124 90011 90130 90011 discrete 90012 90011 continuous 90012 90011 continuous 90012 90011 discrete 90012 90011 discrete 90012 90015 90012 90241 90012 90011 90130 90011 discrete 90012 90011 continuous 90012 90011 discrete 90012 90011 discrete 90012 90011 continuous 90012 90015 90012 90241 90012 90011 90130 90011 {0.1.2} 90012 90011 an interval (a, b) (answers vary) 90012 90011 an interval (a, b) (answers vary) 90012 90011 {4,5,6,7} 90012 90011 {2,3} 90012 90015 90012 90241 90012 90015 90006 4.2 Probability Distributions for Discrete Random Variables 90007 90008 Learning Objectives 90009 90010 90011 To learn the concept of the probability distribution of a discrete random variable.90012 90011 To learn the concepts of the mean, variance, and standard deviation of a discrete random variable, and how to compute them. 90012 90015 90006 Probability Distributions 90007 90002 Associated to each possible value 90003 x 90004 of a discrete random variable 90003 X 90004 is the probability P (x) that 90003 X 90004 will take the value 90003 x 90004 in one trial of the experiment. 90005 90008 Definition 90009 90002 90003 The 90004 probability distributionA list of each possible value and its probability.90003 of a discrete random variable 90004 90003 X 90004 90003 is a list of each possible value of 90004 90003 X 90004 90003 together with the probability that 90004 90003 X 90004 90003 takes that value in one trial of the experiment. 90004 90005 90002 The probabilities in the probability distribution of a random variable 90319 90005.90000 Discrete Random Variables Tutorials & Notes | Machine Learning 90001 90002 In the previous tutorial you got introduced to various concepts of probability. Now let us see how to build functions over the outcomes of a random experiment. 90003 90002 90005 Discrete Random Variables 90006 90007 90003 90002 90005 Def: 90006 90007 A discrete random variable is defined as function that maps the sample space to a set of discrete real values. \ Begin {equation} X: S \ rightarrow {\ rm R} \ End {equation} where X is the random variable, S is the sample space and $$ {\ rm R} $$ is the set of real numbers.Just like any other function, X takes in a value and computes the result according to the rule defined for it. 90003 90002 Elaborating it more, if X is a random variable defined for a certain random experiment with a sample space S, then $$ X = c $$ means the event E containing all possible outcomes $$ e_ {i} \ in S $$ such that $$ X (e_ {i}) = c $$. 90003 90002 90005 Note: 90006 90007 Random variable can take values that are not in sample too. All the values that are not in the sample space are mapped to empty set.90003 90002 90005 Example 1: 90006 90007 From a set of 5 boys and 5 girls, three kids were selected for a painting competition but their genders are not known. Let X be the random variable that denotes the no.of girls selected. What is the event set "c" such that X (c) = 3. 90003 90002 90005 Solution: 90006 90007 X (c) = 3 implies all the outcomes where all the 3 kids selected are girls. c = {(GGG)}. 90003 90002 90005 Probability Mass Function 90006 90003 90002 Probability mass function (pmf) is the probability defined over a given random variable.For a random variable X, p (X = c) is denoted as p (c) and the mapping of each value in sample space to their respective probabilities is known as pmf. For all the values c that are not in sample space, p (c) is pointing towards the probability of an empty set and the value is equal to 0. 90007 90005 Note: 90006 90007 Pmf is just another function that has probability values as results . Hence $$ 0 \ leq p (c) \ leq 1 $$ for any value c. 90003 90002 90005 Example 2: 90006 90007 In continuation to example 1, what is the value of p (3) and also write down the pmf function for random variable X.90003 90002 90005 Solution: 90006 90007 Only case in the sample space that has all three kids as girls is (GGG). The probability of that happening is $$ 1/12 $$. The total pmf is, 90003 90051 90052 90053 90054 $$ a $$ 90055 90054 $$ p (a) $$ 90055 90058 90053 90060 $$ 0 $$ 90061 90060 $$ 1/12 $$ 90061 90058 90053 90060 $$ 1 $$ 90061 90060 $$ 5/12 $$ 90061 90058 90053 90060 $$ 2 $$ 90061 90060 $$ 5/12 $$ 90061 90058 90053 90060 $$ 3 $$ 90061 90060 $$ 1/12 $$ 90061 90058 90083 90084 $$ p (4) = 0 $$ as random variable X can never take the value 4 or for that matter any value greater than 3.90002 90005 Cumulative distribution function 90006 90003 90002 We have seen above that subjecting a random variable to equality leads to pmf. Now what if we deal with inequalities? As per the definition, $$ X \ leq c $$ leads to the event set containing all the outcomes that satisfy the equality condition from $$ - \ infty $$ to $$ c $$. When probability function is applied over such an inequality, it leads to a cumulative probability value giving the estimate of the value being less than or equal to $$ c $$.90003 90002 90005 Def: 90006 90007 Cumulative distribution function (cdf), denoted by CD (c) = $$ \ sum_ {b} p (b) $$ for all $$ - \ infty \ leq b \ leq c $$. 90003 90002 90005 Example: 90006 90007 Continuing the example 2, what is the value of CD (2)? Also calculate the whole CDF for X. 90003 90002 90005 Solution: 90006 90007 $$ CD (2) = p (0) + p (1) + p (2) = 11/12 $$. Complete CDF is as follows: 90003 90051 90052 90053 90054 $$ a $$ 90055 90054 $$ p (a) $$ 90055 90054 $$ CD (a) $$ 90055 90058 90053 90060 $$ 0 $$ 90061 90060 $$ 1/12 $$ 90061 90060 $$ 1/12 $$ 90061 90058 90053 90060 $$ 1 $$ 90061 90060 $$ 5/12 $$ 90061 90060 $$ 6/12 $$ 90061 90058 90053 90060 $$ 2 $$ 90061 90060 $$ 5/12 $$ 90061 90060 $$ 11/12 $$ 90061 90058 90053 90060 $$ 3 $$ 90061 90060 $$ 1/12 $$ 90061 90060 $$ 1 $$ 90061 90058 90083 90084 90002 90005 Some specific distributions 90006 90003 90002 90005 Uniform distribution 90006 90003 90002 Starting with the simplest of all distributions, X = Uniform (N) is used to model the scenarios where all the outcomes are equally possible.For example, the probability of getting a heads or tails are equal in case of a fair coin. So, Uniform (N) implies that there are N outcomes and each has a probability of $$ 1 / N $$. 90003 90002 90005 Bernoulli distribution 90006 90003 90002 Bernoulli distribution is used to model the scenarios in which each trail of random experiment has exactly two possible outcomes. One possible outcomes is termed as 90005 success 90006 and the other as 90005 failure 90006. The main parameter 90005 p 90006 is the probability with success might occur in any trial of the random experiment.X = Bernoulli (p) implies the following points, 90003 90002 Denoting the random variable in binary values, it can take 0 (failure) or 1 (success) value for each trail. 90007 X = 1 is attained with a probability of 90005 p 90006 and X = 0 with a probability of 90005 1-p 90006. 90003 90002 90005 Binomial distribution 90006 90003 90002 Binomial distribution is used to model 90005 n 90006 independent trails of Bernoulli distributions. If X follows Binomial (n, p) then, X = k implies, the event of having k successes in a series of n independent Bernoulli trials.{K} * p \ End {equation} X = k is the event in which the first success was observed after k failures. 90003 90002 Arithmetic rules are applicable to random variables too. They can be added, subtracted or multiplied together. If X and Y follows geometric distribution with same probability p, then X + Y is also a geometric distribution. 90003 90002 90005 Note: 90006 Try to write the PMF tables for each of these distributions! 90003 90002 90005 Expected value 90006 Expected value for a random variable gives the average or mean value calculated over all the possible outcomes of the variable.90007 90005 Def: 90006 90007 If X is a random variable that takes value $$ v_ {i} $$ with a probability of $$ p (v_ {i}) $$ and has a sample space of size n, then the expected value is, \ Begin {equation} E (X) = \ sum_ {n} v_ {i} * p (v_ {i}) \ End {equation} Expected value is often denoted by $$ \ mu $$. 90003 90002 It is clearly evident from the above equation that expected value need not be in the sample space set of the random variable rather it just gives the information about the central tendency of the random variable as a whole.Expected value follows the same when a random variable is multiplied with a scalar or added to other random variable. It also holds for shifting of variable. 90007 $$ E (X + Y) = E (X) + E (Y) $$ 90007 $$ E (cX + d) = c * E (X) + d $$ 90003 90002 90005 Variance and Standard deviation 90006 90003 90002 Expected value is a good measure to represent the random value in a single value. But it also leaves out some vital information that is necessary to understand it better. 90005 Variance 90006 is used to understand the dispersion of probability mass around the mean value of the random value.2) $$$ $$$ \ sigma = \ sqrt (Var (X)) $$$ Where $$ \ sigma $$ is the called the standard deviation. Looking at Var (X) in detail, it is evident that the distance of each value from the mean is squared and it's mean is calculated. This leads to calculation of average distance of the probability mass from the mean value. Square of the distance value is taken to handle the sign of the distances calculated as we only need the magnitude. 90003 90002 Following properties hold for variance of a random variable, 90007 $$ Var (aX + b) = a ^ 2Var (X) $$ 90007 $$ Var (X) = E (X ^ 2) - (E (X)) ^ 2 $$ 90007 $$ Var (X + Y) = Var (X) + Var (Y) $$ iff X and Y are independent.2} $$ 90061 90058 90083 90084 90002 Contributed by: Shubhakar Reddy Tipireddy 90003 .90000 Discrete random variable 90001 90002 by Marco Taboga, PhD 90003 90002 A random variable is said to be discrete if the set of values it can take (its support) has either a finite or an infinite but countable number of elements. Its probability distribution can be characterized through a function called probability mass function. 90003 90002 90007 90003 90009 Definition 90010 90002 The following is a formal definition. 90003 90002 A discrete random variable is often said to have a discrete probability distribution.90003 90009 Examples 90010 90002 Here are some examples. 90003 90019 Example 1 90020 90002 Let 90022 be a random variable that can take only three values (90023, 90024 and 90025), each with probability 90026. Then, 90022 is a discrete variable. Its support is 90028 and its probability mass function is 90029 90003 90002 So, for example, the probability that 90022 will be equal to 90024 is 90034 and the probability that 90022 will be equal to 90036 is 90037 because 90036 does not belong to the support of 90022.90003 90019 Example 2 90020 90002 Let 90022 be a random variable. Let its support be the set of natural natural numbers, that is, 90045 and its probability mass function be 90046 90003 90002 Note that differently from the previous example, where the support was finite, in this example the support is infinite. 90003 90002 What is the probability that 90051 will be equal to 90052? Since 90052 is a natural number, it belongs to the support of 90022 and its probability is 90055 90003 90002 What is the probability that 90051 will be equal to 90059? Since 90059 is not a natural number, it does not belong to the support.As a consequence, its probability is 90061 90003 90009 Probability of a set of numbers 90010 90002 How do we compute the probability that the realization of a discrete variable 90022 will belong to a given set of numbers 90067? 90003 90002 This is accomplished by summing the values of the probability mass function over all the elements of 90067: 90071 90003 90002 Example Consider the variable 90022 introduced in Example 2 above.Suppose we want to compute the probability that 90022 belongs to the set 90076 Then, 90077 90003 90009 Expected value 90010 90002 The expected value of a discrete random variable is computed with the formula 90082 90003 90002 Note that the sum is over the whole support 90085. 90003 90002 Example Consider a variable having support 90088 and probability mass function 90089 Its expected value is 90090 90003 90009 Variance 90010 90002 By using the definition of variance 90095 and the formula for the expected value illustrated in the previous section, we can write the variance of a discrete random random variable as 90096 90003 90002 Example Take the variable in the previous example.We have already calculated its expected value: 90099 Its variance is 90100 90003 90009 Common discrete distributions 90010 90002 The next table contains some examples of discrete distributions that are frequently encountered in probability theory and statistics. 90003 90106 90107 90108 Name of the discrete distribution 90109 90108 Support 90109 90108 Type of support 90109 90114 90107 90116 Bernoulli 90117 90116 {0,1} 90117 90116 Finite 90117 90114 90107 90116 Binomial 90117 90116 {0,1,2 ,..., n} 90117 90116 Finite 90117 90114 90107 90116 Poisson 90117 90116 The set of all non-negative integer numbers 90117 90116 Infinite but countable 90117 90114 90139 90009 More details 90010 90002 You can read a thorough explanation of discrete random variables in the lecture entitled Random variables. 90003 90002 You can also find more details about the probability mass function in this glossary entry.90003 90009 Keep reading the glossary 90010 90002 Previous entry: Design matrix 90003 90002 Next entry: Discrete random vector 90003 .

1. Закон распределения вероятностей дискретной случайной величины.

2. Математическое ожидание дискретной случайной величины.

3. Дисперсия дискретной случайной величины.

4. Функция распределения дискретной случайной величины.

1. Биномиальный закон распределения.

2. Закон распределения Пуассона.

3. Геометрический закон распределения.

4. Гипергеометрический закон распределения.

Функция распределения двумерной случайной величины

Дискретная случайная величина и ее числовые характеристики

Добавить комментарий Отменить ответ