Доверительные интервалы: Доверительные интервалы

Что такое доверительные интервалы?

---

Часто в статистике нас интересует измерение параметров населения — чисел, описывающих некоторые характеристики всего населения.

Двумя наиболее распространенными параметрами населения являются:

1. Среднее значение населения: среднее значение некоторой переменной в популяции (например, средний рост мужчин в США).

2. Доля населения: доля некоторой переменной в населении (например, доля жителей округа, которые поддерживают определенный закон).

Хотя мы заинтересованы в измерении этих параметров, обычно слишком дорого и долго собирать данные о каждом человеке в популяции, чтобы вычислить параметр популяции.

Вместо этого мы обычно берем случайную выборку из общей совокупности и используем данные из выборки для оценки параметра совокупности.

Например, предположим, что мы хотим оценить средний вес определенного вида черепах во Флориде. Поскольку во Флориде тысячи черепах, было бы очень много времени и денег, чтобы обойти и взвесить каждую отдельную черепаху.

Вместо этого мы могли бы взять простую случайную выборку из 50 черепах и использовать средний вес черепах в этой выборке для оценки истинного среднего значения популяции:

Проблема в том, что средний вес черепах в выборке не обязательно точно соответствует среднему весу черепах во всей популяции. Например, мы можем просто случайно выбрать образец, полный черепах с низким весом, или, возможно, образец, полный тяжелых черепах.

Чтобы зафиксировать эту неопределенность, мы можем создать доверительный интервал. Доверительный интервал — это диапазон значений, который может содержать параметр генеральной совокупности с определенным уровнем достоверности. Он рассчитывается по следующей общей формуле:

Доверительный интервал = (точечная оценка) +/- (критическое значение) * (стандартная ошибка)

Эта формула создает интервал с нижней границей и верхней границей, который, вероятно, содержит параметр совокупности с определенным уровнем достоверности.

Доверительный интервал = [нижняя граница, верхняя граница]

Например, формула для расчета доверительного интервала для среднего значения генеральной совокупности выглядит следующим образом:

Доверительный интервал = x +/- z*(s/ √n )

куда:

• x : выборочное среднее
• z: выбранное значение z
• s: стандартное отклонение выборки
• n: размер выборки

Z-значение, которое вы будете использовать, зависит от выбранного вами уровня достоверности. В следующей таблице показано значение z, которое соответствует популярным вариантам выбора уровня достоверности:

| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |

Например, предположим, что мы собираем случайную выборку черепах со следующей информацией:

• Размер выборки n = 25
• Средний вес выборки x = 300
• Стандартное отклонение выборки s = 18,5

Вот как найти вычислить 90% доверительный интервал для истинного среднего веса населения:

90% доверительный интервал: 300 +/- 1,645*(18,5/√25) = [293,91, 306,09]

Мы интерпретируем этот доверительный интервал следующим образом:

Вероятность того, что доверительный интервал [293,91, 306,09] содержит истинный средний вес популяции черепах, составляет 90%.

Другой способ сказать то же самое состоит в том, что существует только 10-процентная вероятность того, что истинное среднее значение генеральной совокупности лежит за пределами 90-процентного доверительного интервала. То есть существует только 10%-ная вероятность того, что истинный средний вес популяции черепах больше 306,09 фунтов или меньше 293,91 фунтов.

Ничего не стоит, что есть два числа, которые могут повлиять на размер доверительного интервала:

1. Размер выборки: чем больше размер выборки, тем уже доверительный интервал.

2. Уровень достоверности: чем выше уровень достоверности, тем шире доверительный интервал.

Существует много типов доверительных интервалов. Вот наиболее часто используемые:

Доверительный интервал для среднего

Доверительный интервал для среднего значения — это диапазон значений, который может содержать среднее значение генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = x +/- z*(s/ √n )

куда:

• x : выборочное среднее
• z: выбранное значение z
• s: стандартное отклонение выборки
• n: размер выборки

Ресурсы: Как рассчитать доверительный интервал для среднего
Доверительный интервал для среднего калькулятора

Доверительный интервал для разницы между средними значениями

Доверительный интервал (ДИ) для разницы между средними значениями представляет собой диапазон значений, который, вероятно, содержит истинное различие между двумя средними значениями генеральной совокупности с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = ( x 1 – x 2 ) +/- t * √ ((s p 2 /n 1 ) + (s p 2 /n 2 ))

куда:

• x 1 , x 2 : среднее значение для образца 1, среднее значение для образца 2
• t: t-критическое значение, основанное на доверительном уровне и (n 1 +n 2 -2) степенях свободы
• s p 2 : объединенная дисперсия
• n 1 , n 2 : размер выборки 1, размер выборки 2

куда:

• Объединенная дисперсия рассчитывается как: s p 2 = ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
• Критическое значение t можно найти с помощью калькулятора обратного t-распределения .

Ресурсы: Как рассчитать доверительный интервал для разницы между средними
Доверительный интервал для калькулятора разницы между средними значениями

Доверительный интервал для пропорции

Доверительный интервал для доли — это диапазон значений, который может содержать долю населения с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = p +/- z * (√ p (1-p) / n )

куда:

• p: доля выборки
• z: выбранное значение z
• n: размер выборки

Ресурсы: Как рассчитать доверительный интервал для пропорции
Доверительный интервал для калькулятора пропорций

Доверительный интервал для разницы в пропорциях

Доверительный интервал для разницы в пропорциях — это диапазон значений, который может содержать истинную разницу между двумя пропорциями населения с определенным уровнем достоверности. Формула для расчета этого интервала:

Доверительный интервал = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )

куда:

• p 1 , p 2 : доля образца 1, доля образца 2
• z: z-критическое значение, основанное на доверительном уровне
• n 1 , n 2 : размер выборки 1, размер выборки 2

Ресурсы: Как рассчитать доверительный интервал для разницы пропорций
Доверительный интервал для калькулятора разницы пропорций

Функция ДОВЕРИТ — Служба поддержки Майкрософт

В этой статье описаны синтаксис формулы и использование  в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

ДОВЕРИТ(альфа;стандартное_откл;размер)

Аргументы функции ДОВЕРИТ описаны ниже.

• Альфа     — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.

• Стандартное_откл     — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.

• Размер     — обязательный аргумент. Размер выборки.

Замечания

• Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

• Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.

• org/ListItem»>

  Если значение аргумента «размер» не является целым числом, оно усекается.

• Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

• Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
0,05	Уровень значимости
2,5	Стандартное отклонение для генеральной совокупности
50	Размер выборки
Формула	Описание	Результат
=ДОВЕРИТ(A2;A3;A4)	Доверительный интервал для математического ожидания генеральной совокупности. Иными словами, доверительный интервал средней продолжительности поездки на работу для генеральной совокупности составляет 30 ± 0,692952 минуты или от 29,3 до 30,7 минут.	0,692951912

Что такое доверительный интервал и как его рассчитать?

Что такое доверительный интервал?

Доверительный интервал в статистике относится к вероятности того, что параметр совокупности будет находиться между набором значений в течение определенного количества раз. Аналитики часто используют доверительные интервалы, которые содержат 95% или 99% ожидаемых наблюдений. Таким образом, если точечная оценка получена на основе статистической модели 10,00 с 95% доверительным интервалом 9,50–10,50, можно сделать вывод, что существует 95% вероятность того, что истинное значение попадает в этот диапазон.

Статистики и другие аналитики используют доверительные интервалы, чтобы понять статистическую значимость своих оценок, выводов или прогнозов. Если доверительный интервал содержит нулевое значение (или какую-либо другую нулевую гипотезу), то нельзя удовлетворительно заявить, что результат данных, полученных в результате тестирования или экспериментов, следует отнести к конкретной причине, а не к случайности.

Основные выводы

• Доверительный интервал показывает вероятность того, что параметр окажется между парой значений около среднего.
• Доверительные интервалы измеряют степень неопределенности или уверенности в методе выборки.
• Они также используются при проверке гипотез и регрессионном анализе.
• Статистики часто используют p-значения в сочетании с доверительными интервалами для оценки статистической значимости.
• Они чаще всего строятся с использованием доверительной вероятности 95% или 99%.

Понимание доверительных интервалов

Доверительные интервалы измеряют степень неопределенности или уверенности в методе выборки. Они могут принимать любое количество пределов вероятности, наиболее распространенным из которых является уровень достоверности 95% или 99%. Доверительные интервалы определяются с использованием статистических методов, таких как t-критерий.

Статистики используют доверительные интервалы для измерения неопределенности выборочной переменной. Например, исследователь случайным образом выбирает разные образцы из одной и той же совокупности и вычисляет доверительный интервал для каждой выборки, чтобы увидеть, как он может представлять истинное значение переменной совокупности. Результирующие наборы данных все разные; некоторые интервалы включают параметр истинной популяции, а другие нет.

Доверительный интервал — это диапазон значений, ограниченный выше и ниже среднего статистического значения, который, вероятно, будет содержать неизвестный параметр генеральной совокупности. Уровень достоверности относится к проценту вероятности или уверенности в том, что доверительный интервал будет содержать истинный параметр генеральной совокупности, когда вы делаете случайную выборку много раз. Или, говоря простым языком, «мы на 99% уверены (уровень достоверности), что большинство этих выборок (доверительные интервалы) содержат истинный параметр совокупности».

Самое большое заблуждение относительно доверительных интервалов заключается в том, что они представляют собой процент данных из данной выборки, которые находятся между верхней и нижней границами. Например, можно ошибочно интерпретировать вышеупомянутый 99% доверительный интервал от 70 до 78 дюймов как указание на то, что 99% данных в случайной выборке попадают между этими числами. Это неверно, хотя для такого определения существует отдельный метод статистического анализа. Для этого необходимо определить среднее значение и стандартное отклонение выборки и нанести эти цифры на кривую нормального распределения.

Доверительный интервал и уровень достоверности взаимосвязаны, но это не одно и то же.

Расчет доверительного интервала

Предположим, группа исследователей изучает рост баскетболистов средней школы. Исследователи берут случайную выборку из населения и устанавливают средний рост 74 дюйма.

Среднее значение 74 дюйма является точечной оценкой среднего значения населения. Точечная оценка сама по себе имеет ограниченную полезность, поскольку она не раскрывает неопределенность, связанную с оценкой; у вас нет четкого представления о том, насколько далеко это 74-дюймовое среднее значение выборки может быть от среднего значения генеральной совокупности. Чего не хватает, так это степени неопределенности в этой единственной выборке.

Доверительные интервалы предоставляют больше информации, чем точечные оценки. Установив 95% доверительный интервал, используя среднее значение выборки и стандартное отклонение, и предполагая нормальное распределение, представленное кривой нормального распределения, исследователи получают верхнюю и нижнюю границы, которые содержат истинное среднее значение в 95% случаев.

Предположим, что интервал составляет от 72 дюймов до 76 дюймов. Если исследователи возьмут 100 случайных выборок из популяции баскетболистов средней школы в целом, среднее значение должно быть между 72 и 76 дюймами за 9 лет.5 таких образцов.

Если исследователям нужна еще большая уверенность, они могут расширить интервал до 99% достоверности.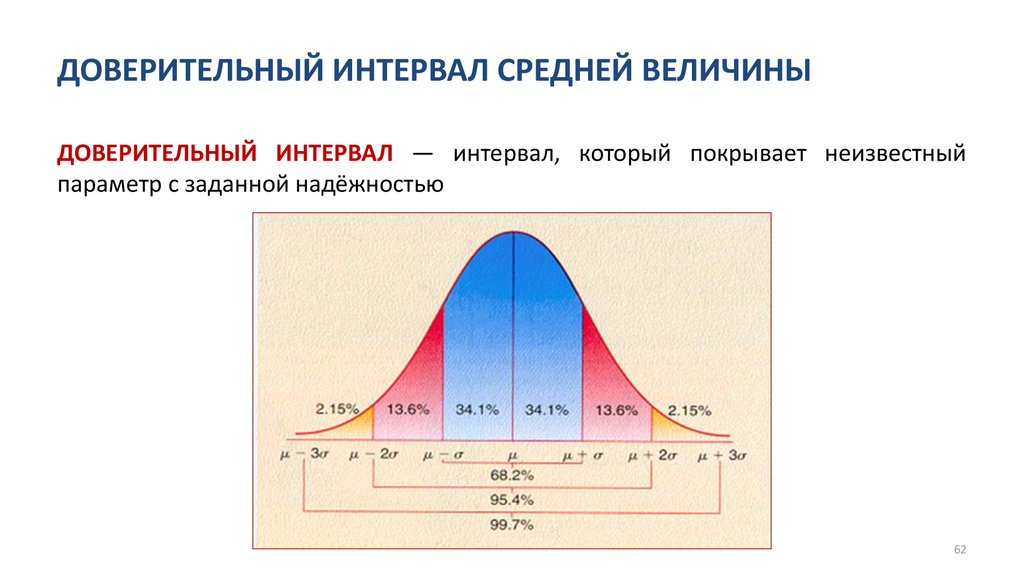 Это неизменно создает более широкий диапазон, поскольку освобождает место для большего количества выборочных средних. Если они установят 99% доверительный интервал между 70 и 78 дюймами, они могут ожидать, что 99 из 100 оцененных образцов будут содержать среднее значение между этими числами.

С другой стороны, уровень достоверности 90% означает, что мы ожидаем, что 90% интервальных оценок будут включать параметр генеральной совокупности и так далее.

Что показывает доверительный интервал?

Доверительный интервал — это диапазон значений, ограниченный выше и ниже среднего статистического значения, который, вероятно, будет содержать неизвестный параметр генеральной совокупности. Уровень достоверности относится к проценту вероятности или уверенности в том, что доверительный интервал будет содержать истинный параметр генеральной совокупности, когда вы делаете случайную выборку много раз.

Для чего используются доверительные интервалы?

Статистики используют доверительные интервалы для измерения неопределенности выборочной переменной. Например, исследователь случайным образом выбирает разные образцы из одной и той же совокупности и вычисляет доверительный интервал для каждой выборки, чтобы увидеть, как он может представлять истинное значение переменной совокупности. Результирующие наборы данных все разные, где некоторые интервалы включают истинный параметр совокупности, а другие нет.

Какое распространенное заблуждение о доверительных интервалах?

Самое большое заблуждение относительно доверительных интервалов состоит в том, что они представляют собой процент данных из данной выборки, которые находятся между верхней и нижней границами. Другими словами, было бы неверным предполагать, что доверительный интервал 99 % означает, что 99 % данных в случайной выборке попадают в эти пределы. На самом деле это означает, что можно быть на 99% уверенным, что диапазон будет содержать среднее значение генеральной совокупности.

Что такое Т-тест?

Доверительные интервалы определяются с использованием статистических методов, таких как t-критерий. Стьюдентный тест — это тип логической статистики, используемый для определения того, существует ли значительная разница между средними значениями двух групп, которая может быть связана с определенными функциями. Для расчета t-критерия требуются три значения ключевых данных. Они включают разницу между средними значениями из каждого набора данных (называемую средней разницей), стандартное отклонение каждой группы и количество значений данных в каждой группе.

Как вы интерпретируете P-значения и доверительный интервал?

Значение p — это статистическое измерение, используемое для проверки гипотезы на основе наблюдаемых данных, которое измеряет вероятность получения наблюдаемых результатов, предполагая, что нулевая гипотеза верна. Как правило, значение p менее 0,05 считается статистически значимым, и в этом случае нулевую гипотезу следует отклонить. Это может в некоторой степени соответствовать вероятности того, что значение нулевой гипотезы (которое часто равно нулю) содержится в 95% доверительный интервал.

Практический результат

Доверительные интервалы позволяют аналитикам понять вероятность того, что результаты статистического анализа являются реальными или случайными. При попытке сделать выводы или прогнозы на основе выборки данных будет некоторая неопределенность в отношении того, действительно ли результаты такого анализа соответствуют изучаемой популяции в реальном мире. Доверительный интервал отображает вероятный диапазон, в пределах которого должно находиться истинное значение.

Понимание доверительных интервалов | Простые примеры и формулы

Опубликован в 7 августа 2020 г. к Ребекка Беванс. Отредактировано 18 ноября 2022 г.

Когда вы делаете оценку в статистике, будь то сводная статистика или тестовая статистика, вокруг этой оценки всегда присутствует неопределенность, поскольку число основано на выборке изучаемой вами совокупности.

Доверительный интервал — это диапазон значений, который, как вы ожидаете, попадет в вашу оценку в определенный процент времени, если вы снова запустите эксперимент или повторите выборку населения таким же образом.

Доверительный уровень — это процент времени, когда вы ожидаете воспроизвести оценку между верхней и нижней границей доверительного интервала, и задается значением альфа.

Содержание

1. Что такое доверительный интервал?
2. Расчет доверительного интервала: что вам нужно знать
3. Доверительный интервал для среднего значения данных с нормальным распределением
4. Доверительный интервал для пропорций
5. Доверительный интервал для данных с ненормальным распределением доверительные интервалы
6. Часто задаваемые вопросы о доверительных интервалах

Что такое доверительный интервал?

Доверительный интервал — это среднее значение вашей оценки плюс и минус вариация этой оценки.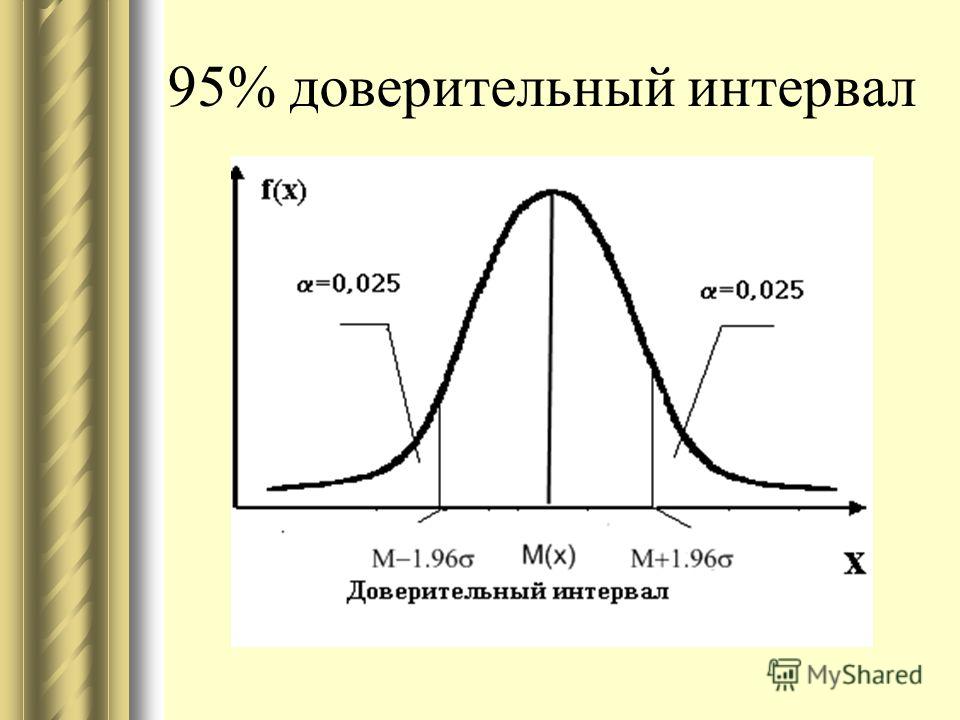 Это диапазон значений, между которыми, как вы ожидаете, будет находиться ваша оценка, если вы повторите тест с определенным уровнем достоверности.

Уверенность , в статистике, это еще один способ описать вероятность. Например, если вы строите доверительный интервал с уровнем достоверности 95 %, вы уверены, что в 95 случаях из 100 оценка попадет между верхним и нижним значениями, указанными в доверительном интервале.

Ваш желаемый уровень достоверности обычно равен единице минус значение альфа (α), которое вы использовали в своем статистическом тесте:

Уровень достоверности = 1 − a

Таким образом, если вы используете значение альфа p < 0,05 для статистической значимости, то ваш уровень достоверности будет 1 − 0,05 = 0,95, или 95%.

Когда вы используете доверительные интервалы?

Вы можете рассчитать доверительные интервалы для многих видов статистических оценок, в том числе:

• Пропорции
• Население означает
• Различия между средними значениями или пропорциями населения
• Оценки различий между группами

Все это точечные оценки, и они не дают никакой информации о вариации числа. Доверительные интервалы полезны для сообщения об отклонении от точечной оценки.

Пример: отклонение от оценки. Вы опросили 100 британцев и 100 американцев об их привычках смотреть телевизор и обнаружили, что обе группы смотрят телевизор в среднем 35 часов в неделю.

Однако у опрошенных британцев наблюдались большие различия в количестве часов просмотра, в то время как у всех американцев наблюдалось одинаковое количество часов.

Несмотря на то, что обе группы имеют одинаковую точечную оценку (среднее количество часов просмотра), британская оценка будет иметь более широкий доверительный интервал, чем американская оценка, поскольку данные больше разнятся.

Расчет доверительного интервала: что нужно знать

Большинство статистических программ включают доверительный интервал оценки при выполнении статистического теста.

Если вы хотите рассчитать доверительный интервал самостоятельно, вам необходимо знать:

1. Точечная оценка, которую вы строите доверительный интервал для
2. Критические значения тестовой статистики
3. Стандартное отклонение выборки
4. Объем выборки

Зная каждый из этих компонентов, вы можете рассчитать доверительный интервал для своей оценки, подставив их в формулу доверительного интервала, соответствующую вашим данным.

Точечная оценка

Точечной оценкой вашего доверительного интервала будет любая статистическая оценка, которую вы делаете (например, среднее значение генеральной совокупности, разница между средними значениями генеральной совокупности, пропорции, различия между группами).

Пример: Оценка в баллах В примере с просмотром телепередач оценка в баллах представляет собой среднее количество часов просмотра: 35.

Нахождение критического значения

Критические значения сообщают вам, на сколько стандартных отклонений от среднего вам нужно уйти, чтобы достичь желаемого уровня достоверности для вашего доверительного интервала.

Есть три шага, чтобы найти критическое значение.

1. Выберите значение альфа (α).

Значение альфа является порогом вероятности для статистической значимости. Наиболее распространенное значение альфа-канала равно 9.0030 p = 0,05, но иногда используются 0,1, 0,01 и даже 0,001. Лучше всего просмотреть исследовательские работы, опубликованные в вашей области, чтобы решить, какое альфа-значение использовать.

2. Решите, нужен ли вам односторонний или двусторонний интервал.

Скорее всего, вы будете использовать двусторонний интервал, если только вы не выполняете односторонний тест t .

Для двустороннего интервала разделите альфу на два, чтобы получить значение альфы для верхнего и нижнего хвостов.

3. Найдите критическое значение, соответствующее альфа-значению.

Если ваши данные подчиняются нормальному распределению или у вас есть большой размер выборки ( n > 30), который примерно нормально распределен, вы можете использовать распределение z , чтобы найти критические значения.

Для статистики z некоторые из наиболее распространенных значений показаны в этой таблице:

Уровень достоверности	90%	95%	99%
альфа для одностороннего CI	0,1	0,05	0,01
альфа для двустороннего CI	0,05	0,025	0,005
z статистика	1,64	1,96	2,57

Если вы используете небольшой набор данных (n ≤ 30) с приблизительно нормальным распределением, используйте т дистрибутив вместо.

Распределение t имеет ту же форму, что и распределение z , но с поправкой на небольшие размеры выборки. Для распределения t вам необходимо знать свои степени свободы (размер выборки минус 1).

Ознакомьтесь с набором таблиц t , чтобы найти статистику t . Мы включили уровень достоверности и значения p как для односторонних, так и для двусторонних тестов, чтобы помочь вам найти t нужное вам значение.

Для нормальных распределений, таких как распределение t и распределение z , критическое значение одинаково по обе стороны от среднего.

Пример: критическое значение. В опросе о просмотре телепередач насчитывается более 30 наблюдений, и данные следуют примерно нормальному распределению (колоколообразная кривая), поэтому мы можем использовать распределение z для нашей тестовой статистики.

Для двустороннего 95% доверительного интервала значение альфа равно 0,025, а соответствующее критическое значение равно 1,9. 6.

Это означает, что для расчета верхней и нижней границ доверительного интервала мы можем взять среднее значение ±1,96 стандартного отклонения от среднего.

Определение стандартного отклонения

Большинство статистических программ имеют встроенную функцию для расчета стандартного отклонения, но чтобы найти его вручную, вы можете сначала найти дисперсию выборки, а затем извлечь квадратный корень, чтобы получить стандартное отклонение.

1. Найти выборочную дисперсию

Выборочная дисперсия определяется как сумма квадратов отличий от среднего, также известная как среднеквадратическая ошибка (MSE):

Чтобы найти MSE, вычтите среднее значение выборки из каждого значения в наборе данных, возведите полученное число в квадрат и разделите это число на n − 1 (размер выборки минус 1).

Затем сложите все эти числа, чтобы получить общую выборочную дисперсию ( s ² ). Для больших выборок проще всего это сделать в Excel.

2. Найдите стандартное отклонение.

Стандартное отклонение вашей оценки ( s ) равно квадратному корню выборочной дисперсии/ошибки выборки ( s ² ):

 

Пример: стандартное отклонение. В опросе телезрителей дисперсия оценки Великобритании составляет 100, а дисперсия оценки США — 25. Извлечение квадратного корня из дисперсии дает нам стандартное отклонение выборки ( с ) из:

• 10 для оценки ГБ.
• 5 для оценки США.

Размер образца

Размер выборки — это количество наблюдений в вашем наборе данных.

Пример: Размер выборки В нашем опросе американцев и британцев размер выборки составляет 100 человек для каждой группы.

Что может сделать корректура для вашей статьи?

Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в статье не было неясных выражений, избыточных слов и неудобных формулировок.

См. пример редактирования

Доверительный интервал для среднего значения нормально распределенных данных

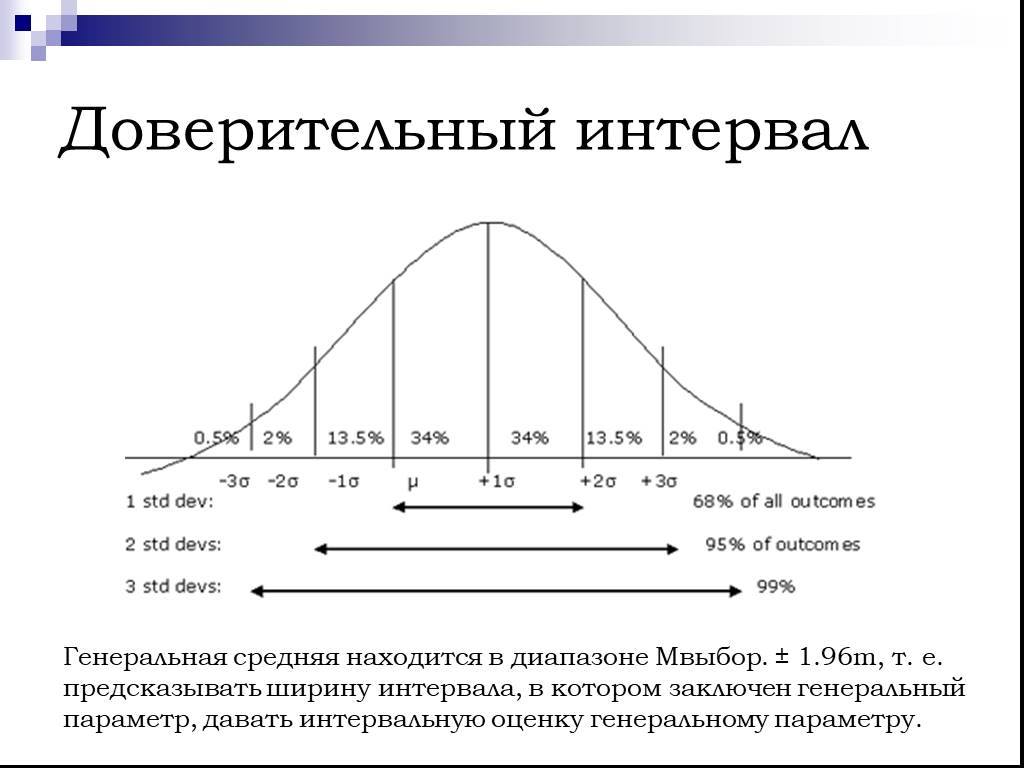
Нормально распределенные данные образуют форму колокола при нанесении на график со средним значением выборки в середине, а остальные данные распределены достаточно равномерно по обе стороны от среднего.

Доверительный интервал для данных, соответствующих стандартному нормальному распределению:

Где:

• ДИ = доверительный интервал
• X̄ = среднее значение населения
• Z* = критическое значение распределения z
• σ = стандартное отклонение совокупности
• √n = квадратный корень из численности населения

Доверительный интервал для распределения t следует той же формуле, но заменяет Z * на t *.

В реальной жизни вы никогда не узнаете истинные значения численности населения (если только вы не можете провести полную перепись).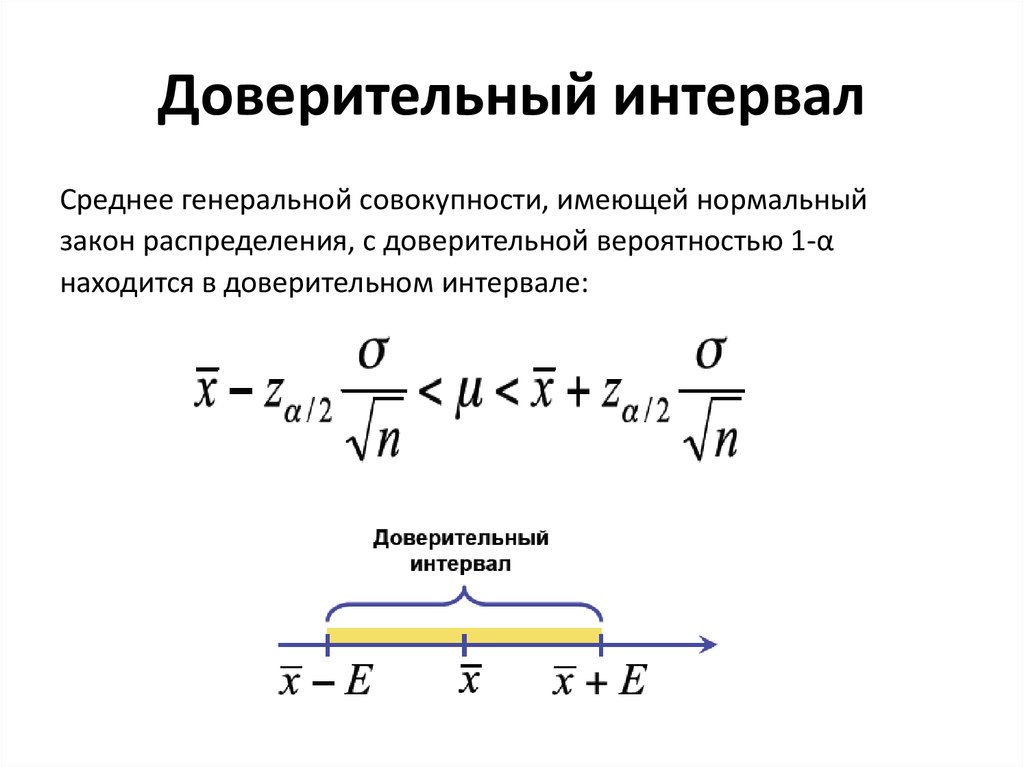 Вместо этого мы заменяем значения генеральной совокупности значениями из наших выборочных данных, поэтому формула принимает следующий вид:

Где:

• ˆx = выборочное среднее
• с = стандартное отклонение выборки

Пример: расчет доверительного интервала. В исследовании привычек американцев и британцев смотреть телевизор мы можем использовать среднее значение выборки, стандартное отклонение выборки и размер выборки вместо среднего значения генеральной совокупности, стандартного отклонения генеральной совокупности и размера генеральной совокупности.

Чтобы вычислить 95% доверительный интервал, мы можем просто подставить значения в формулу.

Для США:

   

Итак, для США нижняя и верхняя границы 95% доверительного интервала равны 34,02 и 35,98.

Для ГБ:

   

Таким образом, для ГБ нижняя и верхняя границы 95% доверительного интервала составляют 33,04 и 36,96.

Доверительный интервал пропорций

Доверительный интервал для пропорции следует той же схеме, что и доверительный интервал для средних, но вместо стандартного отклонения вы используете пропорцию выборки, умноженную на единицу, минус пропорцию:

Где:

• ˆp = доля в вашей выборке (например, доля респондентов, которые вообще не смотрели телевизор)
• Z*= критическое значение распределения z
• n = объем выборки

Доверительный интервал для ненормально распределенных данных

Чтобы вычислить доверительный интервал вокруг среднего значения данных, которые не имеют нормального распределения, у вас есть два варианта:

1. Вы можете найти распределение, соответствующее форме ваших данных, и использовать это распределение для расчета доверительного интервала.
2. Вы можете выполнить преобразование данных, чтобы привести их к нормальному распределению, а затем найти доверительный интервал для преобразованных данных.

Выполнение преобразований данных очень распространено в статистике, например, когда данные следуют логарифмической кривой, но мы хотим использовать их вместе с линейными данными. Вам просто нужно не забыть выполнить обратное преобразование ваших данных, когда вы вычисляете верхнюю и нижнюю границы доверительного интервала.

Отчетные доверительные интервалы

Доверительные интервалы иногда приводятся в статьях, хотя исследователи чаще сообщают о стандартном отклонении своих оценок.

Если вас попросят указать доверительный интервал, вы должны указать верхнюю и нижнюю границы доверительного интервала.

Пример: отчет о доверительном интервале «Мы обнаружили, что и в США, и в Великобритании в среднем 35 часов просмотра телевизора в неделю, хотя оценка для Великобритании была более вариативной (9 часов). 5% ДИ = 33,04, 36,96), чем для США (95% ДИ = 34,02, 35,98)».

Одним из мест, где часто используются доверительные интервалы, являются графики. При отображении различий между группами или построении линейной регрессии исследователи часто включают доверительный интервал, чтобы дать визуальное представление о вариации вокруг оценки.

Пример: доверительный интервал на графике. Вы можете нанести точечные оценки среднего количества часов просмотра телевизора в США и Великобритании с 95% доверительный интервал вокруг среднего значения.

Внимание при использовании доверительных интервалов

Доверительные интервалы иногда интерпретируются как говорящие о том, что «истинное значение» вашей оценки находится в пределах доверительного интервала.

Это не так. Доверительный интервал не может сказать вам, насколько вероятно, что вы нашли истинное значение вашей статистической оценки, потому что она основана на выборке, а не на всей совокупности.

Доверительный интервал только говорит вам, какой диапазон значений вы можете ожидать, если вы повторно сделаете выборку или проведете эксперимент снова точно таким же образом.

Чем точнее ваш план отбора проб или реалистичнее ваш эксперимент, тем выше вероятность того, что ваш доверительный интервал включает истинное значение вашей оценки. Но эта точность определяется вашими методами исследования, а не статистикой, которую вы делаете после того, как собрали данные!

Часто задаваемые вопросы о доверительных интервалах

Чем отличается доверительный интервал от доверительного уровня?

Уровень достоверности — это процент случаев, когда вы ожидаете приблизиться к той же оценке, если вы снова запустите эксперимент или повторите выборку населения таким же образом.

Доверительный интервал состоит из верхней и нижней границ оценки, которую вы ожидаете получить при заданном уровне достоверности.

Например, если вы оцениваете 95-процентный доверительный интервал вокруг средней доли младенцев женского пола, рождающихся каждый год на основе случайной выборки младенцев, вы можете найти верхнюю границу 0,56 и нижнюю границу 0,48. Это верхняя и нижняя границы доверительного интервала. Уровень достоверности 95%.

Как рассчитать доверительный интервал?

Для расчета доверительного интервала необходимо знать:

• Точечную оценку, которую вы строите доверительный интервал для
• Критические значения тестовой статистики
• Стандартное отклонение выборки
• Размер выборки

Затем вы можете подставить эти компоненты в формулу доверительного интервала, соответствующую вашим данным. Формула зависит от типа оценки (например, среднее значение или пропорция) и от распределения ваших данных.

Что такое z-показатели и t-показатели?

z -score и t -score (также известные как z -значение и t -value) показывают, на сколько стандартных отклонений от среднего значения распределения вы находитесь, предполагая, что ваши данные соответствуют распределению z . или т -распределение.

Эти баллы используются в статистических тестах, чтобы показать, насколько далека от среднего значения прогнозируемого распределения ваша статистическая оценка. Если ваш тест дает z -оценку 2,5, это означает, что ваша оценка составляет 2,5 стандартных отклонения от предсказанного среднего значения.

Прогнозируемое среднее значение и распределение вашей оценки генерируются нулевой гипотезой статистического теста, который вы используете. Чем больше стандартных отклонений от предсказанного среднего в вашей оценке, тем меньше вероятность того, что оценка могла быть получена при нулевой гипотезе.

Что такое критическое значение?

Критическое значение — это значение статистики теста, которое определяет верхнюю и нижнюю границы доверительного интервала или порог статистической значимости в статистическом тесте. Он описывает, как далеко от среднего значения распределения вам нужно пройти, чтобы охватить определенное количество общей вариации данных (т. е. 90%, 95%, 99%).

Если вы строите 95% доверительный интервал и используете порог статистической значимости p = 0,05, то ваше критическое значение будет одинаковым в обоих случаях.

Что означает, если мой доверительный интервал включает ноль?

Если ваш доверительный интервал для различий между группами включает ноль, это означает, что при повторном проведении эксперимента у вас есть хорошие шансы не обнаружить различий между группами.

Если ваш доверительный интервал для корреляции или регрессии включает ноль, это означает, что если вы снова запустите свой эксперимент, есть большая вероятность, что в ваших данных не будет найдено никакой корреляции.

В обоих этих случаях вы также обнаружите высокое значение p при выполнении статистического теста, что означает, что ваши результаты могли быть получены при нулевой гипотезе об отсутствии связи между переменными или отсутствии различий между группами.

No related posts.