Нахождение вектора, перпендикулярного данному вектору, примеры и решения
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
Определение 1При условии значения угла между двумя ненулевыми векторами равным 90°( π2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Теорема 1Скалярное произведение двух ненулевых векторов a→ и b→ равном нулю для выполнения равенства a→, b→=0 достаточно для их перпендикулярности.
Доказательство 1Пусть заданные векторы a→ и b→ перпендикулярны, тогда выполним доказательство равенства a⇀, b→=0.
Из определения про скалярное произведение векторов мы знаем, что оно равняется произведению длин заданных векторов на косинус угла между ними. По условию a→ и b→ перпендикулярны, а, значит, исходя из определения, угол между ними 90°.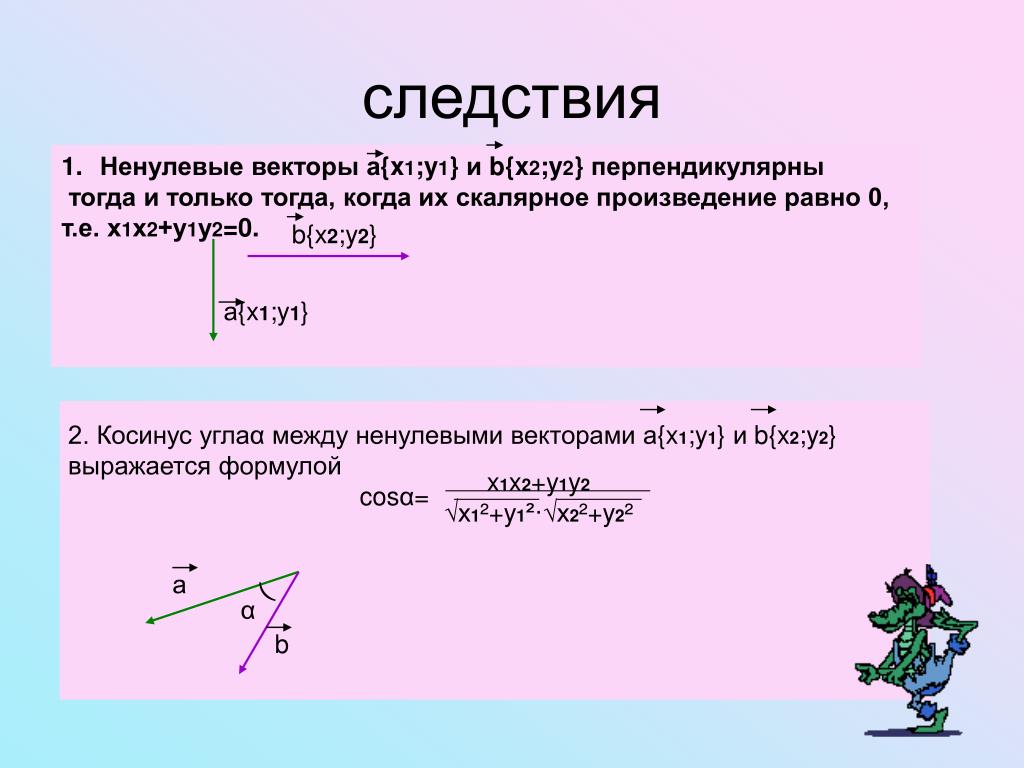
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство (a→, b→)=ax·bx+ay·by, справедливое для векторов с координатами a→=(ax, ay) и b→=(bx, by), на плоскости и (a→,b→)=ax·bx+ay·by для векторов a→=(ax, ay, az) и b→=(bx, by, bz) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид ax·bx+ay·by=0, для трехмерного пространства ax·bx+ay·by+az·bz=0.
Применим на практике и рассмотрим на примерах.
Пример 1Проверить свойство перпендикулярности двух векторов a→=(2, -3), b→=(-6, -4).
Решение
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
(a→, b→)=ax·bx+ay·by=2·(-6)+(-3)·(-4)=0. Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a→ и b→ перпендикулярны.
Пример 2Даны координатные векторы i→, j→, k→. Проверить, могут ли векторы i→-j→ и i→+2·j→+2·k→ быть перпендикулярными.
Решение
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i→-j→ и i→+2·j→+2·k→ имеются соответствующие координаты (1,-1, 0) и (1, 2, 2). Подставляем числовые значения и получаем: i→+2·j→+2·k→, i→-j→=1·1+(-1)·2+0·2=-1.
Выражение не равно нулю, (i→+2·j→+2·k→, i→-j→)≠0, а это означает, что векторы i→-j→ и i→+2·j→+2·k→ не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i→-j→ и i→+2·j→+2·k→ не перпендикулярны.
Пример 3Даны векторы a→=(1,0,-2) и b→=(λ, 5, 1). Найти значение λ, при котором данные векторы перпендикулярны.
Решение
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
ax·bx+ay·by+az·bz=0 ⇔1·λ+0·5+(-2)·1=0 ⇔λ=2
Ответ: векторы перпендикулярны при значении λ=2.
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 4Дан треугольник АВС со сторонами АВ=8, АС=6, ВС=10 см. проверить на перпендикулярность векторы AB→ и AC→.
Решение
При перпендикулярности векторов AB→ и AC→ треугольник ABC считается прямоугольным. Тогда применим теорему Пифагора, где ВС – гипотенуза треугольника. Равенство BC2=AB2+AC2 должно выполниться. Отсюда следует, что 102=82+62⇔100=100. Значит, АВ и АС являются катетами треугольника АВС, следовательно, AB→ и AC→ перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a→ может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Задан ненулевой вектор a→, лежащий на прямой а. Тогда заданный b→, расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным иa→. Если вектору i→ перпендикулярен вектор j→ или любой из векторов λ·j→при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b→, перпендикулярному a→=(ax, ay), сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a→=(ax, ay). Для этого необходимо записать условие перпендикулярности векторов в такой форме ax·bx+ay·by=0. Имеем bx и by , являющиеся искомыми координатами перпендикулярного вектора. Когда ax≠0, значение by является ненулевым, а bx вычислим из неравенства ax·bx+ay·by=0 ⇔bx=-ay·byax.
Дан вектор с координатами a→=(-2, 2). Найти перпендикулярный данному вектор.
Решение
Обозначим искомый вектор как b→(bx, by). Найти его координаты можно из условия перпендикулярности векторов a→ и b→. Тогда получим: (a→, b→)=ax·bx+ay·by=-2·bx+2·by=0. Присвоим by=1 и подставим: -2·bx+2·by=0⇔-2·bx+2=0. Отсюда из формулы получим bx=-2-2=12. Значит, вектор b→=(12, 1) является вектором, перпендикулярным a→.
Ответ: b→=(12, 1).
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a→=(ax, ay, az) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a→ , лежащая на прямой a. Перпендикулярную прямой a плоскость обозначаем α. В этом случае любой ненулевой вектор b→ из плоскости α перпендикулярен a→.
Необходимо найти координаты b→, перпендикулярного ненулевому вектору a→=(ax, ay, az).
Пусть задан b→ с координатами bx, by и bz. Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство ax·bx+ay·by+az·bz=0 должно выполняться. Из условия a→ — ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что ax≠0, ( ay≠0 или az≠0). Следовательно, имеем право разделить на эту координату все неравенство ax·bx+ay·by+az·bz=0, получим выражениеbx+ay·by+az·bzax=0⇔bx=-ay·by+az·bzax. Присваиваем координатам by и bx любое значение, вычисляем значение bx, исходя из формулы, bx=-ay·by+az·bzax. Искомый перпендикулярный вектор будет иметь значение a→=(ax, ay, az).
Рассмотрим доказательство на примере.
Пример 6Дан вектор с координатами a→=(1, 2, 3) . Найти вектор, перпендикулярный данному.
Решение
Обозначим искомый вектор за b→=(bx, by, bz). Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a⇀, b⇀=0⇔ax·bx+ay·by+az·bz=0⇔1·bx+2·by+3·bz=0⇔bx=-(2·by+3·bz)
Если значение by=1, bz=1, тогда bx=-2·by-3·bz=-(2·1+3·1)=-5. Отсюда следует, что координаты вектора b→(-5, 1, 1). Вектор b→ является одним из перпендикулярных векторов заданному.
Отсюда следует, что координаты вектора b→(-5, 1, 1). Вектор b→ является одним из перпендикулярных векторов заданному.
Ответ: b→=(-5, 1, 1).
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторамa→(ax, ay, az) и b→=(bx, by, bz). При условии коллинеарности векторов a→ и b→ в задаче достаточно будет найти вектор, перпендикулярный a→ или b→.
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a→ и b→ называют вектор, одновременно перпендикулярный и a→ и b→. Для решения данной задачи применяется векторное произведение a→×b→. Для трехмерного пространства имеет вид a→×b→=a→j→k→axayazbxbybz
Разберем подробнее векторное произведение на примере задачи.
Пример 7 Заданы векторы b→=(0, 2, 3) и a→=(2, 1, 0). Найти координаты любого перпендикулярного вектора данным одновременно.
Решение
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a→×b→=i→j→k→210023=i→·1·3+j→·0·0+k→·2·2-k→·1·0-j→·2·3-i→·0·2=3·i→+(-6)·j→+4·k→
Ответ: (3, -6, 4) — координаты вектора, одновременно перпендикулярного заданным a→ и b→.
Перпендикулярность векторов, условие перпендикулярности, примеры
Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.
Координаты вектора на плоскости, равного по модулю и перпендикулярного данному
Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Алгоритм получения координат перпендикулярных векторов
Вектор на плоскости xOy, перпендикулярный данному вектору получают так:
- Поменять местами координатные числа «x» и «y».
- Заменить знак у одной из координат на противоположный.
Графический пример
Рассмотрим небольшой графический пример (рис. 1).
Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом
На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: \(\vec{a}\) и \(\vec{b}\).
\[ \vec{a} = \left\{ 4 ; 3 \right\} \]
\[ \vec{b} = \left\{ -3 ; 4 \right\} \]
Из рисунка видно, что векторы \(\vec{a}\) и \(\vec{b}\) перпендикулярны: \( \vec{a} \perp \vec{b} \).
Вектор \( -\vec{b} = \left\{ 3 ; -4 \right\} \), также будет перпендикулярным вектору \( \vec{a} \): \( \vec{a} \perp \vec{(-b)} \)
Векторы, изображенные черным цветом, перпендикулярны красному вектору.
Длины векторов \( \vec{a} \), \( \vec{b} \) и \( \vec{(-b)} \) равны.
Условие перпендикулярности векторов
Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.
Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.
Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.
\[ \large \boxed { \begin{cases} \vec{a} = \left\{ a_{x} ; a_{y} ; a_{z} \right\} \\ \vec{b} = \left\{ b_{x} ; b_{y} ; b_{z} \right\} \\ |\vec{a}| \ne 0 \\ |\vec{b}| \ne 0 \end{cases}}\]
Запишем условие перпендикулярности векторов.
Для двумерного случая:
\[ \large \boxed { a_{x} \cdot b_{x} + a_{y} \cdot b_{y} = 0 }\]
Для трехмерного случая:
\[ \large \boxed { a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} = 0 }\]
Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.
При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.
Примечание:
Есть такое правило: Количество неизвестных должно равняться количеству уравнений.
Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.
Перпендикулярные векторы в физике
В физике перпендикулярность некоторых векторов достаточно важна.
Вот несколько примеров:
- Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
- На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
- Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.

- Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
- На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).
Как доказать что векторы перпендикулярны
Ключевые слова:
перпендикулярность, прямая линия, параллельность, вектор, коллинеарные вектора, координаты
Условие перпендикулярности векторов
Условие коллинеарности векторов
См. также:
Углы на плоскости, Координаты вектора
Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.
Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( радиан).
Для перпендикулярности двух ненулевых векторов и необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .
Пусть векторы и перпендикулярны. Докажем выполнение равенства .
По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы и перпендикулярны, то угол между ними равен девяноста градусам, следовательно, , что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что . Докажем, что векторы и перпендикулярны.
Так как векторы и ненулевые, то из равенства следует, что . Таким образом, косинус угла между векторами и равен нулю, следовательно, угол равен , что указывает на перпендикулярность векторов и .
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Как же выглядит условие перпендикулярности двух векторов в координатной форме?
В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами и на плоскости справедливо равенство , а для двух векторов и в пространстве . Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид на плоскости, а в трехмерном пространстве .
Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид на плоскости, а в трехмерном пространстве .
Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.
Перпендикулярны ли векторы .
Вычислим их скалярное произведение по координатам . Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
да, векторы перпендикулярны.
Перпендикулярны ли векторы и , где – координатные векторы прямоугольной системы координат в трехмерном пространстве.
Векторы и имеют соответственно координаты и (при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:
Так как , то векторы и не перпендикулярны.
нет, не перпендикулярны.
Найдите значение , при котором векторы и перпендикулярны.
Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме
векторы перпендикулярны при .
В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.
Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы и перпендикулярны.
Если векторы и перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство . Проверим его справедливость: .
Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы и перпендикулярны.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – | 7538 – или читать все.
А чужой храп его отдаляет. 8828 – | 7538 – или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Скалярное произведение двух ненулевых векторов a → и b → равном нулю для выполнения равенства a → , b → = 0 достаточно для их перпендикулярности.
Пусть заданные векторы a → и b → перпендикулярны, тогда выполним доказательство равенства a ⇀ , b → = 0 . векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.
Условие перпендикулярности на координатной плоскости
Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .
Применим на практике и рассмотрим на примерах.
Проверить свойство перпендикулярности двух векторов a → = ( 2 , – 3 ) , b → = ( – 6 , – 4 ) .
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
( a → , b → ) = a x · b x + a y · b y = 2 · ( – 6 ) + ( – 3 ) · ( – 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → – j → и i → + 2 · j → + 2 · k → быть перпендикулярными.
Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → – j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , – 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → – j → = 1 · 1 + ( – 1 ) · 2 + 0 · 2 = – 1 .
Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → – j → ) ≠ 0 , а это означает, что векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.
Ответ: нет, векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Даны векторы a → = ( 1 , 0 , – 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.
Найти значение λ , при котором данные векторы перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( – 2 ) · 1 = 0 ⇔ λ = 2
Ответ: векторы перпендикулярны при значении λ = 2 .
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .
При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 . Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = – a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = – a x · b x a y .
Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = – a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = – a x · b x a y .
Дан вектор с координатами a → = ( – 2 , 2 ) . Найти перпендикулярный данному вектор.
Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = – 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: – 2 · b x + 2 · b y = 0 ⇔ – 2 · b x + 2 = 0 . Отсюда из формулы получим b x = – 2 – 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .
Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .
Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .
Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .
Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = – a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = – a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .
Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .
Рассмотрим доказательство на примере.
Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.
Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.
a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = – ( 2 · b y + 3 · b z )
Если значение b y = 1 , b z = 1 , тогда b x = – 2 · b y – 3 · b z = – ( 2 · 1 + 3 · 1 ) = – 5 . Отсюда следует, что координаты вектора b → ( – 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.
Ответ: b → = ( – 5 , 1 , 1 ) .
Нахождение координат вектора, перпендикулярного двум заданным векторам
Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .
При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .
При решении применяется понятие векторного произведения векторов.
Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z
Разберем подробнее векторное произведение на примере задачи.
Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 – k → · 1 · 0 – j → · 2 · 3 – i → · 0 · 2 = 3 · i → + ( – 6 ) · j → + 4 · k →
Ответ: ( 3 , – 6 , 4 ) – координаты вектора, одновременно перпендикулярного заданным a → и b → .
Ортогональность векторов.
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = {ax; ay} и b = {bx; by}, условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by = 0
Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = {ax; ay; az} и b = {bx; by; bz}, условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by + az · bz = 0
Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 42n — 4 = 0
2n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Скалярное произведение векторов. Формулы и определение
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно.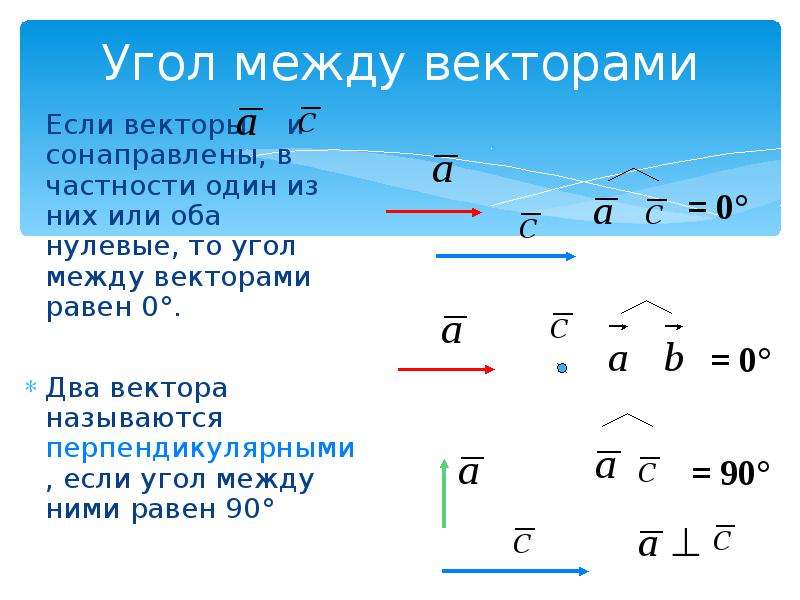 Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Значок угла ∠ можно опустить и писать просто: (→a;→b).
Пусть даны два вектора →a, →b.
Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
- Алгебраическая интерпретация.

Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0 так как , то есть cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
- Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
- Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
Так как:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
откуда
- Вспомнив формулу вычисления длины вектора по координатам, получаем
- Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.
- Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.

Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + … + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
- Скалярное произведение вектора самого на себя всегда больше или равно нулю.
 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору.→а * →а > 0
→0 * →0 = 0
- Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
- Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
- Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
- Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
- Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 <=> a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay.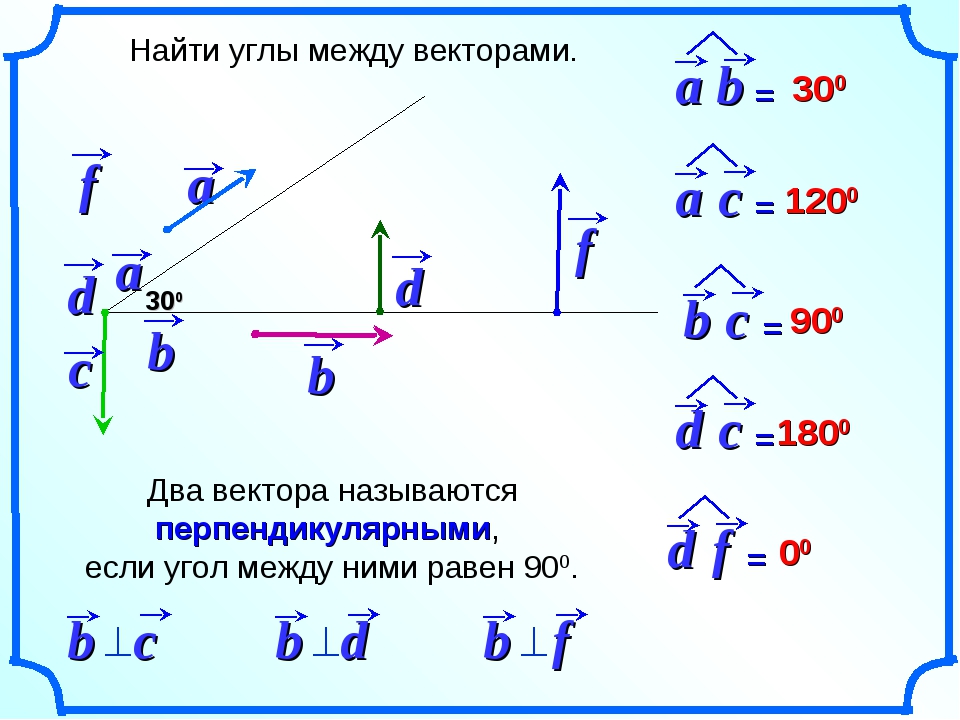 В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
и,
откуда следует:
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Как решаем:
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Ответ: →a * →b = 5√3.
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: (→a,→b) = 411.
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Как решаем:
- Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
- Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
- Найдем координаты векторов →AB1 и →BC1:
- Найдем длины векторов →AB1 и →BC1:
- Найдем скалярное произведение векторов →AB1 и →BC1:
- Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Урок 2. скалярное произведение векторов — Геометрия — 11 класс
Геометрия, 11 класс
Урок № 2. Скалярное произведение векторов
Перечень вопросов, рассматриваемых в теме:
— ввести понятие угла между векторами и скалярного произведения векторов, рассмотреть формулу скалярного произведения в координатах;
— показать применение скалярного произведения векторов при решение задач.
— рассмотреть основные свойства скалярного произведения;
— сформировать умения вычислять скалярное произведение векторов и находить угол между векторами;
— показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, а также между прямой и плоскостью.
Глоссарий по теме:
Два вектора называются перпендикулярными, если угол между ними равен 90°.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Формула вычисления скалярного произведения векторов по определению:
Формула вычисления скалярного произведения векторов через координаты:
Основная литература:
Гусева В.А., Куланин Е.Д. Геометрия. Профильный уровень. 10 класс — М.: Бином, 2010 — с. 130-148
Погорелов А.В. Геометрия. Учеб. для 7-11 кл. общеобразоват. Учреждение — 13-е изд-е. — М.: Просвещение, 2014. — с. 51-52
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 кл. 20-е изд-е. — М.: Просвещение, 2010. — с. 259-270.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Работа по теме урока. Объяснение новой темы
Объяснение новой темы
Угол между векторами
Если векторы не являются сонаправленными, то лучи ОА и ОB образуют угол АОВ.
Определение: Два вектора называются перпендикулярными, если угол между ними равен 90°.
Скалярное произведение векторов:
Определение: Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Запишем формулу:
Доказательство утверждений:
Утверждение1. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Утверждение2. Скалярный квадрат вектора равен квадрату его длины.
Формула скалярного произведения двух векторов и
Через их координаты
Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.
Угол между векторами.
Косинус угла между векторами пространства , заданными в ортонормированном базисе , выражается формулой:
Сформулируем основные свойства скалярного произведения векторов.
Для любых векторов и любого числа k справедливы равенства:
1) причем при
2) (переместительный закон).
3) (распределительный закон).
4) (сочетательный закон).
Вычисление углов между прямыми и плоскостями.
Угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Дано: прямоугольный параллелепипед, где . Найти и .
Решение: ранее в таких случаях мы пытались по рисунку находить величины углов.
Но теперь мы владеем формулой косинуса угла между прямыми.
Только для этого необходимо знать координаты направляющих векторов прямых. В данном случае, для прямой BD направляющим может является вектор BD , а для прямой
CD- CD вектор (рис. 15)
Для удобства изобразим прямоугольную систему координат так, чтобы точка B совпадала с точкой начала координат.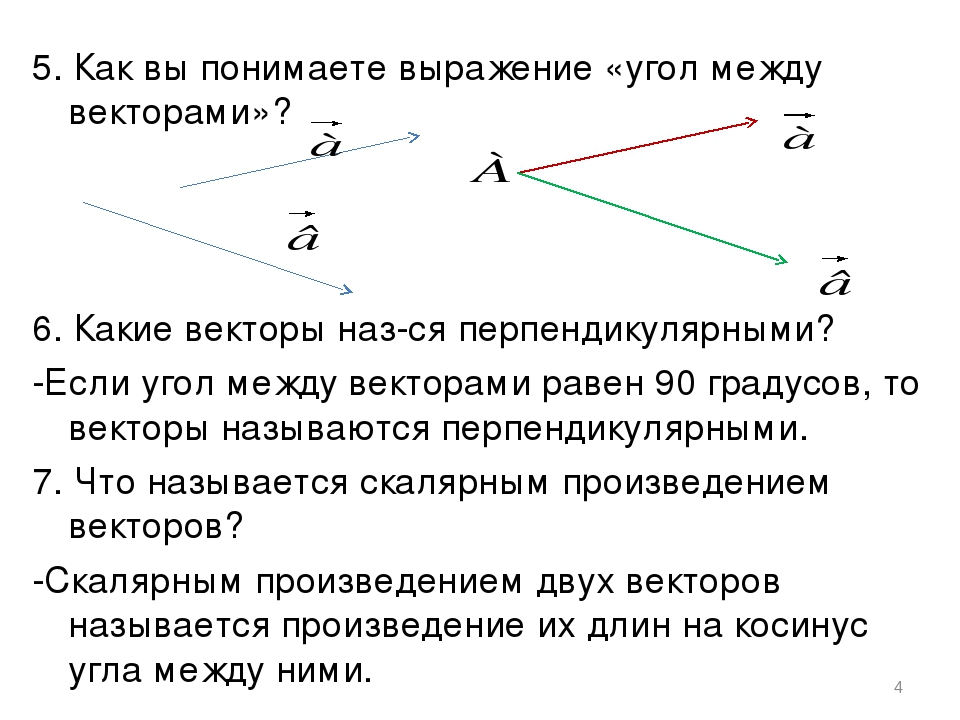 Взяв длину рёбер AB и BC за единичные отрезки, можно утверждать, что длина отрезка BB равна 2.
Взяв длину рёбер AB и BC за единичные отрезки, можно утверждать, что длина отрезка BB равна 2.
Тогда не трудно определить координаты точек B, D, C и D1.
Точка B(0;0;0). Точка D(1;1;0). Точка C(0;1;0) . А точка D(1;1;2).
Теперь не трудно найти координаты векторовBD и CD как разности соответствующих координат конца и начала вектора.
Получаем, что вектор BD {1-0;1-0;0-0}. А вектор
CD{1-0;1-1;2-0}.
Теперь можем воспользоваться формулой косинуса угла между прямыми. Подставим координаты направляющих векторов.
Рис. 15
Ответ:
Пример 2.
Дано: DABC – пирамида; DA ⊥ DB ⊥ DC; DA = DB = DC = а.
Найдите: косинус угла между прямыми DC и CM (СМ – высота треугольника АВС), поставьте ему в соответствие верный вариант ответа из предложенных ниже:
Решение:
Треугольник АВС правильный, поэтому тоска М является серединой стороны АВ.
Введем систему координат как показано на рисунке.
Найдем координаты векторов
Применив формулу косинуса угла между векторами, получим .
Ответ:
Ортогональность векторов.
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = {ax; ay} и b = {bx; by} условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by = 0
Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = {ax; ay; az} и b = {bx; by; bz} условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by + az · bz = 0
Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 42n — 4 = 0
2n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Определить, являются ли два вектора параллельными или перпендикулярными
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Расчет— выяснение, перпендикулярны ли два вектора или параллельны
исчисление — выяснение, являются ли два вектора перпендикулярными или параллельными — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 72к раз
$ \ begingroup $ Я не уверен, что правильно понял. {- 1} (\ frac {v_1.v_2} {| v_1 || v_2 |}) $$
если $ \ theta = 0 $ или $ 180 $, два вектора параллельны
{- 1} (\ frac {v_1.v_2} {| v_1 || v_2 |}) $$
если $ \ theta = 0 $ или $ 180 $, два вектора параллельны
, если $ \ theta = 90 $, два вектора перпендикулярны
Создан 13 июн.
E.H.EE.H.E22.8k11 золотых знаков2424 серебряных знака7575 бронзовых знаков
$ \ endgroup $ 4 $ \ begingroup $Два вектора $ v_1 = (x_1, y_1) $ и $ v_2 = (x_2, y_2) $ параллельны, если $ x_1 \, y_2 = x_2 \, y_1 $.
Данвил24511 серебряных знаков1313 бронзовых знаков
Создан 13 июн.
2,11388 серебряных знаков1818 бронзовых знаков
$ \ endgroup $ 2 $ \ begingroup $Два вектора параллельны, если они скалярно кратны друг другу.Другими словами, если вы можете умножить один вектор на константу и получить другой вектор.
Грубая причина этого в том, что умножение на скаляр вообще не поворачивает вектор (оно может растягивать или переворачивать вектор, но не меняет направление).
Создан 13 июн.
ptrsinclairptrsinclair41622 серебряных знака88 бронзовых знаков
$ \ endgroup $ $ \ begingroup $ Они параллельны тогда и только тогда, когда они различаются в i раз. е. (1,3) и (-2, -6).
Для перпендикулярных векторов скалярное произведение будет равно 0, то есть они пересекаются точно под углом 90 градусов.
е. (1,3) и (-2, -6).
Для перпендикулярных векторов скалярное произведение будет равно 0, то есть они пересекаются точно под углом 90 градусов.
Когда вы вычисляете скалярное произведение и ваш ответ отличен от нуля, это просто означает, что два вектора не перпендикулярны.
Создан 13 июн.
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
доказывает, что два вектора перпендикулярны
Мы можем немного использовать аналитическую геометрию, чтобы помочь в описании векторов для этой проблемы.(Не очень полезно выполнять полное определение всех соответствующих координат точек, так как координаты ключевых точек усложняются.) Удобно разместить одну сторону треугольника на оси $ \ x- $, при этом, скажем, точка $ \ A \ $ в начале координат; другой вершине $ \ C \ $ с этой стороны мы дадим координаты $ \ (c, 0) \ \. $ Если мы дадим третьей вершине $ \ B \ $ координаты $ \ (a, b) \ \, $, то высота, сброшенная с этой вершины, будет вертикальным отрезком прямой, пересекающимся с $ \ AC \ $ в точке $ \ F (a, 0) \ \.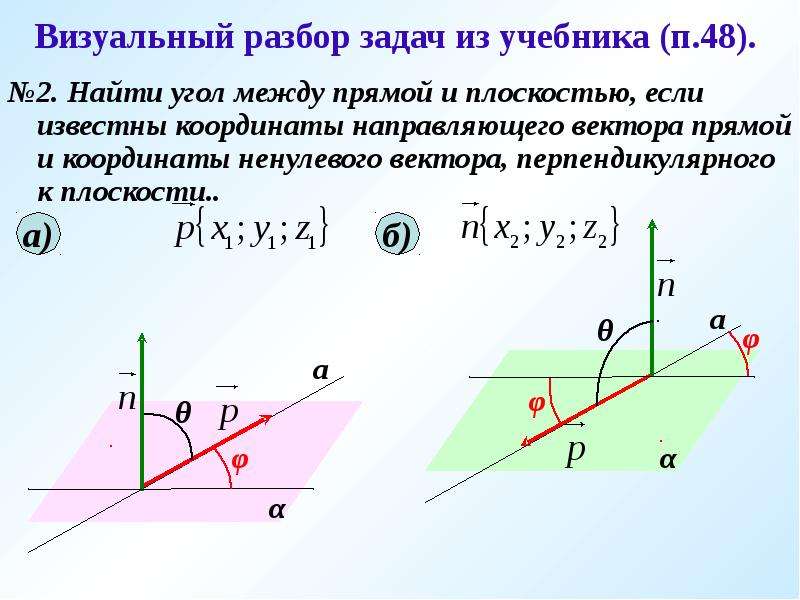 $
$
Тогда у нас есть векторы $ \ \ overrightarrow {AB} \ = \ \ langle a \, \ b \ rangle \ $ и $ \ \ overrightarrow {CB} \ = \ \ langle (a — c) \, \ b \ проложить \ $ по соответствующим сторонам треугольника. Вектор $ \ overrightarrow {AG} \ $ перпендикулярен $ \ \ overrightarrow {CB} \ $: мы располагаем $ \ overrightarrow {AG} \ \ cdot \ \ overrightarrow {CB} \ = \ 0 \ $ на назначая направление $ \ \ overrightarrow {AG} \ = \ \ langle b \, \ — (a — c) \ rangle \ = \ \ langle b \, \ (c — a) \ rangle \ \.$
Нам потребуются координаты еще одной точки, $ \ D \, $, чтобы установить направление вектора $ \ \ overrightarrow {CD} \ \. $ Мы используем $ \ overrightarrow {AG} \ $, чтобы получить параметрические уравнения для линии, на которой она лежит, $$ x \ = \ 0 \ + \ b · t \ \, \ \ y \ = \ 0 \ + \ (c-a) · t \ \.
$Но поскольку $ \ D \ $ лежит на высоте $ \ \ overline {BF} \ $, его координата $ \ x- $ равна $ \ x = a \ \, $, таким образом,
$$ a \ = \ bt \ \ \ Rightarrow \ \ t \ = \ \ frac {a} {b} \ \ \ Rightarrow \ \ y \ = \ \ frac {a · (ca)} {b} \ \ .
Теперь мы можем указать направление $ \ \ overrightarrow {CD} \ $, которое также является направлением $ \ \ overrightarrow {CE} \ $, как $$ \ \ overrightarrow {CD} \ = \ \ langle (a — c) \, \ left (\ frac {a · (c-a)} {b} — 0 \ right) \ rangle \ \.
$Отсюда находим $$ \ overrightarrow {AB} \ \ cdot \ \ overrightarrow {CE} \ \ = \ \ \ langle a \, \ b \ rangle \ \ cdot \ \ langle (a — c) \, \ frac {a · (ca)} {b} \ rangle \ \ = \ \ a · (ac) \ + \ a · (ca) \ \ = \ \ 0 \ \.
$Мы заключаем, что $ \ overrightarrow {AB} \ \ perp \ \ overrightarrow {CE} \ \.$
Урок КАК доказать, что два вектора в координатной плоскости перпендикулярны
КАК доказать, что два вектора в координатной плоскости перпендикулярны
Предположим, что два вектора u и v заданы в координатной плоскости в компонентной форме u = (a, b) и v = (c, d).
Как доказать, что эти векторы парпендикулярны?
Два вектора u = (a, b) и v = (c, d) в координатной плоскости перпендикулярны тогда и только тогда, когда их скалярное произведение a * c + b * d равно нулю : А * с + Ь * г = 0.
Пример 1
Докажите, что векторы u = (,) и v = (,) перпендикулярны.
Раствор
Скалярное произведение этих векторов равно
( u , v ) = * — * = 3 — 3 = 0.
Поскольку скаляр векторов u и v равен нулю, эти векторы перпендикулярны.
Пример 2
Докажите, что векторы u = (,) и v = (,) перпендикулярны.
Раствор
Скалярное произведение этих векторов равно
( u , v ) = + = — = — = 0.
Поскольку скаляр векторов u и v равен нулю, эти векторы перпендикулярны.
Для справки см. Урок «Перпендикулярные векторы в координатной плоскости» в теме Введение в векторы, сложение и масштабирование раздела Алгебра-II на этом сайте.
Мои уроки по Dot-продукту на этом сайте
— Введение в точечное произведение
— Формула скалярного произведения векторов на плоскости через компоненты векторов
— Точечное произведение векторов в координатной плоскости и угла между двумя векторами
— Перпендикулярные векторы в координатной плоскости
— Решенные задачи по скалярному произведению векторов и углу между двумя векторами.
— Свойства скалярного произведения векторов в координатной плоскости
— Формула угла между двумя векторами и формула косинусов разности двух углов
Есть короткие уроки « КАК.. . Тип «на точечном продукте:
— КАК найти скалярное произведение двух векторов на плоскости
— КАК найти скалярное произведение двух векторов в координатной плоскости
— КАК найти угол между двумя векторами в координатной плоскости
— КАК доказать, что два вектора в координатной плоскости перпендикулярны (этот урок)
— КАК ДОКАЗАТЬ, что треугольник в координатной плоскости является прямоугольным треугольником
— КАК проверить, является ли четырехугольник в координатной плоскости параллелограммом
— КАК проверить, является ли четырехугольник в координатной плоскости прямоугольником
— КАК проверить, является ли четырехугольник в координатной плоскости ромбом
— КАК проверить, является ли четырехугольник в координатной плоскости квадратом
Полный список моих уроков по точечному продукту с короткими аннотациями см. В файле ОБЗОР уроков по дот-продукту.
В файле ОБЗОР уроков по дот-продукту.
Используйте этот файл / ссылку ALGEBRA-II — YOUR ONLINE TEXTBOOK для навигации по всем темам и урокам онлайн-учебника ALGEBRA-II.
Почему точечное произведение двух перпендикулярных векторов равно нулю?
С прошлой недели я учил себя некоторой линейной алгебре по книге Эрика Лендьеля Математика для программирования трехмерных игр и компьютерной графики . Одна из тем, которую я недавно узнал, касается скалярного произведения векторов. Скалярное произведение — это просто длина проекции одного вектора на другой вектор.Вы можете думать о проекции как о тени проецируемого вектора на другой вектор, где источник света перпендикулярен и указывает на другой вектор. На картинке ниже показана визуализация того, что я только что описал. На изображении ниже \ (P \) и \ (Q \) — это 2D-векторы. Обратите внимание, что проекция также является другим вектором.
Скалярное произведение определяется как:
, где \ (P \) и \ (Q \) — \ (n \) -мерные векторы. Из одного определения мы можем видеть, что скалярное произведение — это просто сумма произведений каждого компонента из каждого вектора.Например, предположим, что у нас есть два 2D-вектора, \ (P = \ langle 2, 3 \ rangle \) и \ (Q = \ langle 4, 2 \ rangle \). Скалярное произведение этих двух векторов будет выглядеть следующим образом.
Из одного определения мы можем видеть, что скалярное произведение — это просто сумма произведений каждого компонента из каждого вектора.Например, предположим, что у нас есть два 2D-вектора, \ (P = \ langle 2, 3 \ rangle \) и \ (Q = \ langle 4, 2 \ rangle \). Скалярное произведение этих двух векторов будет выглядеть следующим образом.
Одно свойство, которое мы можем получить из скалярного произведения, состоит в том, что всякий раз, когда мы получаем скалярное произведение двух перпендикулярных векторов, результат равен нулю. Почему это так? Мы можем использовать базовое определение скалярного произведения, чтобы ответить на этот вопрос, но использование другого определения предоставит нам другую перспективу, которая даст нам немного более глубокое понимание того, почему это так.Но что это за другое определение?
Прежде чем я прямо отвечу на этот вопрос, давайте сначала попробуем что-нибудь еще. Возьмем снова два вектора, \ (P \) и \ (Q \). Давайте создадим вектор, который начинается с головы \ (P \) и заканчивается в голове \ (Q \).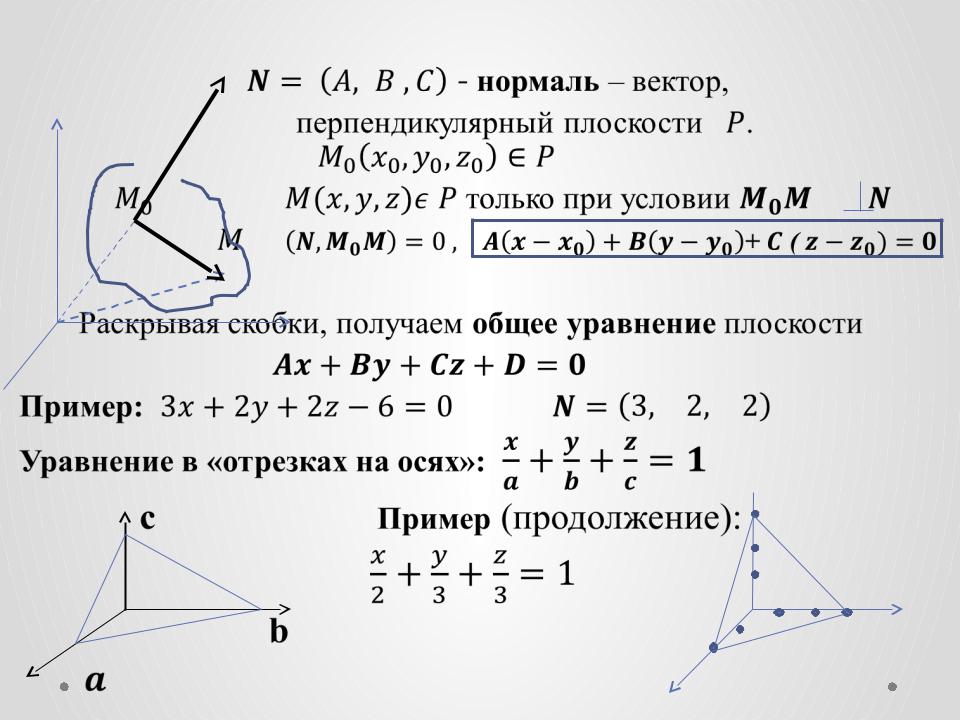 Примечательно, что мы получаем вектор, который представляет собой просто \ (P — Q \), и треугольник, составленный из трех векторов.
Примечательно, что мы получаем вектор, который представляет собой просто \ (P — Q \), и треугольник, составленный из трех векторов.
А теперь поиграем с длиной, также известной как величина вектора \ (P — Q \). Помните, что величина вектора \ (P \) обозначается как \ (\ left | \ left | P \ right | \ right | \) и определяется уравнением ниже.В некоторых текстах для величины используется \ (| P | \). Я не рекомендую использовать это обозначение, потому что его можно спутать с абсолютным значением. Кроме того, внимательно изучив приведенное ниже уравнение, вы заметите, что определение величины основано на теореме Пифагора.
Интересно, что это не единственное уравнение для длины \ (P — Q \). Поскольку у нас есть треугольник, мы можем использовать тригонометрию для определения длины. Закон косинусов позволяет получить другое уравнение для длины.{2} \).)
Как видно из приведенных выше выражений, мы смогли получить другое определение скалярного произведения, \ (P \ cdot Q = \ left | \ left | P \ right | \ right | \ left | \ left | Q \ право | \ право | \ соз (\ альфа) \). Здесь все становится интересно. Помните, что всякий раз, когда две линии или вектора перпендикулярны друг другу, угол между ними всегда будет \ (90 ° \). Таким образом, для двух перпендикулярных векторов \ (\ alpha = 90 \). Теперь взгляните на \ (\ cos (\ alpha) \) часть уравнения.Давайте заменим \ (\ alpha \) в \ (\ cos (\ alpha) \) на \ (90 \). Это дает нам \ (\ cos (90 °) \), результат которого равен \ (0 \). Применяя эти знания ко второму определению имеющегося у нас скалярного произведения, мы получаем:
Здесь все становится интересно. Помните, что всякий раз, когда две линии или вектора перпендикулярны друг другу, угол между ними всегда будет \ (90 ° \). Таким образом, для двух перпендикулярных векторов \ (\ alpha = 90 \). Теперь взгляните на \ (\ cos (\ alpha) \) часть уравнения.Давайте заменим \ (\ alpha \) в \ (\ cos (\ alpha) \) на \ (90 \). Это дает нам \ (\ cos (90 °) \), результат которого равен \ (0 \). Применяя эти знания ко второму определению имеющегося у нас скалярного произведения, мы получаем:
И, таким образом, причина, по которой два перпендикулярных вектора имеют скалярное произведение \ (0 \). Если вы еще не уверены, вот альтернативный способ взглянуть на это. Давайте воспользуемся теневой аналогией, приведенной в начале этой статьи. Как обычно, у нас есть источник света, перпендикулярный проектируемому вектору.Однако, как показано на изображении ниже, поскольку вектор, который мы проецируем, параллелен источнику света, тень не будет отбрасываться на другой вектор. Отсутствие тени означает, что длина проекции равна нулю. Таким образом, скалярное произведение двух перпендикулярных векторов равно нулю, что отвечает на наш вопрос.
Отсутствие тени означает, что длина проекции равна нулю. Таким образом, скалярное произведение двух перпендикулярных векторов равно нулю, что отвечает на наш вопрос.
Во многих случаях в математике математическое понятие не обязательно имеет только одну формулу, описывающую его. Используя законы и логически звучащую математическую гимнастику, мы можем придумывать формулы, определяющие одно и то же понятие.Мы наблюдали такое явление в этой статье с помощью скалярного произведения. Мы видели, что есть другое определение для скалярного произведения. И благодаря этому мы смогли выяснить объяснение того, почему у перпендикулярных векторов скалярное произведение равно нулю. Новое определение, которое мы получили, поможет нам понять более сложные концепции линейной алгебры. Для тех из нас, кто изучает линейную алгебру, эти знания — еще одна ступенька, которая приведет нас к лучшему пониманию линейной алгебры. Пришло время перейти к другим темам линейной алгебры.А что касается тех, кто наткнулся на это просто из любопытства, эй, вы узнали что-то новое сегодня (надеюсь), и приятно узнать что-то новое.
Точка и крестное произведение — Вопросы и ответы по электромагнитной теории
Этот набор вопросов и ответов с множественным выбором (MCQ) по электромагнитной теории посвящен теме «Точка и кросс-произведение».
1. Когда два вектора перпендикулярны, их
a) Точечное произведение равно нулю
b) Перекрестное произведение равно нулю
c) Оба вектора равны нулю
d) Оба вектора не обязательно равны нулю
Посмотреть ответ
Ответ: a
Объяснение: точка произведение двух перпендикулярных векторов дается А.B = | a || b | cos 90, что равно нулю. Таким образом, скалярное произведение равно нулю, а векторы перпендикулярны.
2. Произведение векторов 3i + 4j — 5k и –i + j — 2k равно,
a) 3i — 11j + 7k
b) -3i + 11j + 7k
c) -3i — 11j — 7k
d) -3i + 11j — 7k
Посмотреть ответ
Ответ: b
Объяснение: Произведение двух векторов равно AXB = (a2 * b3 — b2 * a3) i — (a1 * b3 — b1 * a3) j + (a1 * b2 — b1 * a2) k. Используя формулу, можно рассчитать ответ.
Используя формулу, можно рассчитать ответ.
3. Что из следующего не является векторными функциями в электромагнетизме?
a) Градиент
b) Дивергенция
c) Curl
d) В Electromagnetics нет не векторных функций
View Answer
Answer: d
Объяснение: Поскольку все координаты в электромагнитном являются пространственными координатами, направление и величина важный.Таким образом, все функции являются только векторными.
4. Произведенная работа векторов силы F и расстояния d, разделенных углом θ, может быть вычислена с помощью,
a) Произведение
b) Точечное произведение
c) Сложение двух векторов
d) Невозможно вычислить
Посмотреть ответ
Ответ: b
Объяснение: Сила — это векторная величина, а расстояние — скалярное. Работа определяется как произведение силы и расстояния, которое выражается скалярным произведением.
5. Определите, параллельны ли векторы, (-2,1, -1) и (0,3,1)
a) Параллельно
b) Коллинеарно параллельно
c) Непараллельно
d) Недостаточно данных
Посмотреть ответ
Ответ: c
Объяснение: Два вектора параллельны, если их перекрестное произведение равно нулю. Поскольку их перекрестное произведение равно 4i + 2j — 6k (ненулевое), векторы не параллельны.
Поскольку их перекрестное произведение равно 4i + 2j — 6k (ненулевое), векторы не параллельны.
6. Сила Лоренца основана на,
a) Точечное произведение
b) Перекрестное произведение
c) Как скалярное произведение, так и перекрестное произведение
d) Независимо от обоих
Посмотреть ответ
Ответ: b
Объяснение: Сила Лоренца определяется как, F = q (vx B) .Таким образом, кросс-произведение является ответом.
7. Электромагнитные силы определяются правилом
a) Правило правой руки Флеминга
b) Правило левой руки Флеминга
c) Закон Фарадея
d) Закон Ампера
Посмотреть ответ
Ответ: b
Пояснение: Три пальца левой руки обозначают электрические поле, магнитное поле и распространение волны в свободном пространстве аналогично силе, магнитному полю и току соответственно в любом проводнике.
8. Скалярное произведение двух векторов является скаляром. Перекрестное произведение двух векторов — это вектор. Состояние Истина / Ложь.
Состояние Истина / Ложь.
a) Верно
b) Неверно
Просмотреть ответ
Ответ: a
Объяснение: Точечное произведение — это алгебраическая операция, которая берет две последовательности равной длины и возвращает скаляр. Перекрестное произведение — это двоичная операция, которая вычисляет площадь двух векторов, то есть векторную величину.
9. Какая из теорем Пифагора верна в электромагнетизме?
a) | скалярное произведение | + | точечный продукт | = 1
б) | перекрестное произведение | — | перекрестное произведение | = 1
c) | скалярное произведение | 2 + | перекрестное произведение | 2 = 1
d) | скалярное произведение | + | перекрестное произведение | = 0
Посмотреть ответ
Ответ: c
Пояснение: Option | dot product | 2 + | перекрестное произведение | 2 = 1 дает | cos | 2 + | грех | 2 = 1, и это правильный ответ.
10. Что из следующего неверно?
а) А. (B. C) = скалярное значение
(B. C) = скалярное значение
b) A. (B x C) = скалярное значение
c) A x (B. C) = скалярное значение
d) A x (B x C) = векторное значение
Просмотреть ответ
Ответ: c
Пояснение: произведение скалярных произведений из двух векторов является векторным значением.
Sanfoundry Global Education & Learning Series — Электромагнитная теория.
Чтобы практиковать все области электромагнитной теории, вот полный набор из 1000+ вопросов и ответов с множественным выбором .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Как узнать, перпендикулярны ли два вектора?
Показана трапеция A B C D. Диагонали проводятся от точки B к точке D и от точки A к точке C и пересекаются в точке E. Если четырехугольник ABCD равен … равнобедренная трапеция, какие утверждения должны быть верными? Выберите три варианта BC ∥ AD BD ⊥ AC BA ≅ CD BE ED ∠CBA ≅ ∠BCD
Найдите уравнение прямой с m = 6 и b = -7. Запишите уравнение в форме пересечения наклона.
Запишите уравнение в форме пересечения наклона.
Найдите ответ на вопрос b, проверьте правильность а и объясните, пожалуйста
Два угла дополняют друг друга (сумма двух углов составляет 90 °). Сумма первого угла плюс удвоенный второй угол составляет 150 °. Найдите меры … углы.
Если x2 + 3xy + 2y3 = 7, то в терминах x и y dy / dx =
Каков наклон прямой, проходящей через (-5, -10) и (-1, 5)
Учитывая следующие наборы, ответьте на следующие вопросы A-enF = x / x — буква от слова LOVE) B = A B C DG-S, I, O, NC-CO, V, ERH = x / x — это левая
… tter из алфавита D = {C, O, U, G, H} I = {остаться, дома, сохранить, выжить} EES.INGJ = {делиться, любить и заботиться} 1. Каковы подмножества множества A? 2. Каковы правильные подмножества набора A? 3. Каковы несобственные подмножества множества A? 4. Каково общее количество подмножеств в наборе A? 5. Каковы эквиваленты набора B? 6. Что это за набор E и G? 7. Что это за набор C и D? 8. Что это за набор I и J? 9. Какой набор установлен F? 10. Какая сеть установлена H?
Что это за набор I и J? 9. Какой набор установлен F? 10. Какая сеть установлена H?
Показана трапеция A B C D. Диагонали проводятся от точки B к точке D и от точки A к точке C и пересекаются в точке E.Если четырехугольник ABCD равен … равнобедренная трапеция, какие утверждения должны быть верными? Выберите три варианта BC ∥ AD BD ⊥ AC BA ≅ CD BE ED ∠CBA ≅ ∠BCD
Радж читает 7/12 своей книги перед обедом и еще 2/12 своей книги после обеда
Для небольших обучающих наборов дисперсия может вносить больший вклад в общую ошибку, чем смещение. Иногда это достигается за счет уменьшения сложности режима. … л, даже если модель слишком простая. Как вы думаете, почему это так
.




 В результате получается нуль, если вектор равен нулевому вектору.
В результате получается нуль, если вектор равен нулевому вектору.