Это угол между векторами: Угол между векторами

Содержание

Нахождение угла между векторами: понятие, правила

Заголовок статьи дает много информации о материале, который будет изложен далее. Он достаточно прост для понимания, однако важный и нужный в дальнейшем обучении. На его основе будут формулироваться все следующие понятия и решаться различные задачи на плоскости, осуществляться вычисления.

Однако, чтобы решать математические и физические задачи, такого представления недостаточно. Данные понятия следует определить более строго, точно следуя всем правилам математической науки.

Воспользуемся графической иллюстрацией. Это нам поможет рассмотрение вопроса сделать более наглядным. Для отличия от скалярных величин, будем обозначать векторы жирным шрифтом.

Пусть имеются два ненулевых вектора a и b. На плоскости они или в трёхмерном пространстве сейчас не особо важно. Пусть наши векторы OA = a и OB = b имеют общее начало в некоторой точке O.

Определение 1

Под углом между векторами a и b понимается угол между двумя лучами OA и OB. Обозначим его как (a, b), т. е. курсивом и жирным одновременно.

Ясно, что угол между нашими векторами может принимать значения от нуля градусов до 180 градусов. Часто в математике углы обозначают не в градусах, а в радианах. Угол в 90 градусов равен π/2 радиан. Угол в 180 градусов, как не трудно предположить равняется π радиан.

Угол между a и b равен нулю градусам, когда они являются сонаправленными, и 180 градусам или π радиан, когда противоположно направлены.

Определение 2

Векторы a и b перпендикулярны, если угол между ними составляет π/2 радиан.

В случае, когда один из векторов нулевой, угол между ними считается неопределённым.

О нахождение угла между векторами

Нахождение угла между векторами или (что по сути тоже самое) нахождение косинуса угла между векторами можно осуществить с помощью скалярного произведения векторов или воспользовавшись теоремой косинусов для треугольника на указанных векторах.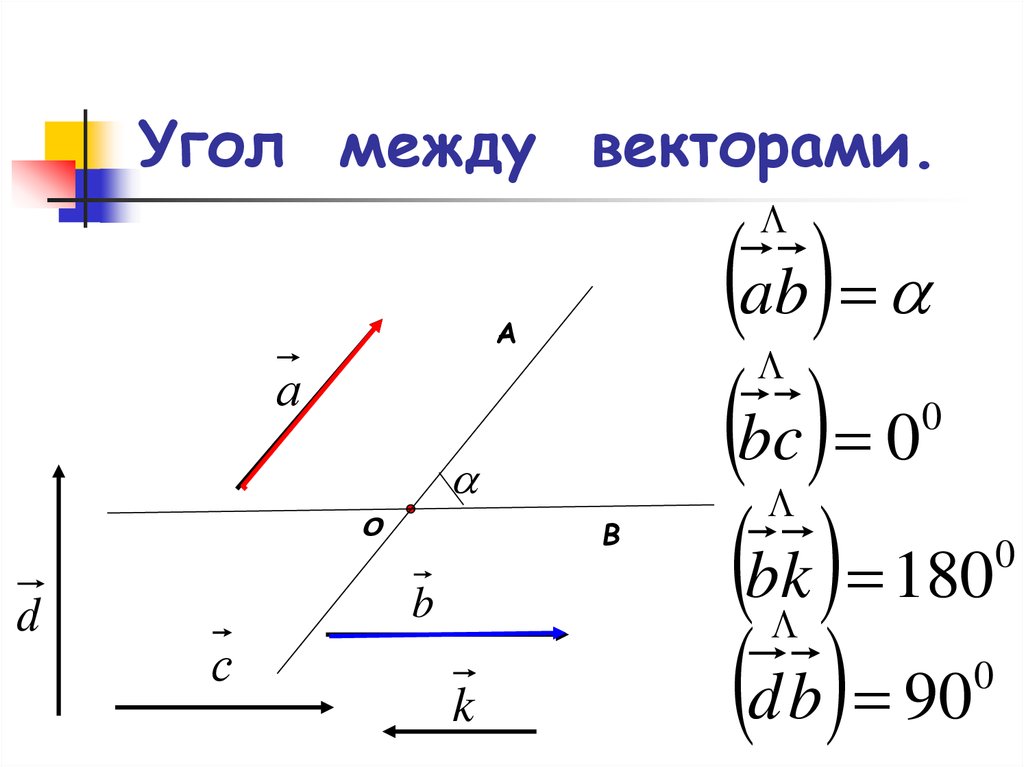

Напомним, что скалярное произведение a и b есть результат умножения их длин на косинус угла между векторами. Формулой это записывается так:

(a, b) = a*b*cos (a, b)

Исходим из того что ни один из векторов a и b не равен нулю. В этом случае косинус можно найти просто, разделив скалярное произведение на длины векторов.

cos (a, b) = (a, b)/(a*b)

Это есть формула нахождения косинуса угла между векторами. Провести нахождение угла между двумя векторами после этого труда не составляет.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Примеры задач на нахождение угла между векторами

Пример. 1 . Пусть у нас имеются векторы a и b. Пусть по длине один из них равен 4, а другой 8. Скалярное произведения наших векторов равно (-12). Подставляя указанные значения в формулу для косинуса, можно легко провести его вычисление

cos (a, b) = -12/(4*8) = — ½

Чтобы найти сам угол, нужно вычислить арккосинус полученного нами значения.

(a,b) = arcos (-1/2) = 3π/4

Ответ: Запишем его виде cos (a, b) = — ½, (a,b) = 3π/4.

Часто векторы задаются не так, как в примере выше, а с помощью координат в прямоугольной декартовой системе координат. Для этого требуется формула нахождения угла между векторами в координатной форме.

Напомним, что длина вектора определяется, как сумма квадратов его координат, а скалярное произведение векторов представляет собой сумму произведения их соответствующих координат.

a = (a_x, a_y), b = (b_x, b_y)

\[ \cos (a, b)=\frac{\left(a_{x} * b_{x}+a_{y}^{*} b_{v}\right)}{\sqrt{a_{x}^{2}+a_{y}^{2}} \sqrt{b_{x}^{2}+b_{y}^{2}}} \]

Нахождение угла между векторами в трёхмерном пространстве происходит аналогичным образом, только мы имеем вектора с координатами не «x, y», а с координатами «x, y, z». {2}}} \]

Пример. 2. Пусть у нас имеется прямоугольная декартова система координат и в ней векторы

a = (3, 0, -4) и b = (1, 3, 4)

Мы должны провести нахождение угла между этими векторами по координатам.

Сделаем расчёт сначала по формуле для координат векторов, затем с помощью скалярного произведения векторов. В принципе обе формулы полностью равноценны между собой. Здесь мы намеренно расписываем всё максимально подробно.

Выясним, чему будет равно скалярное произведения наших векторов в их координатной записи. Перемножаем их x-координаты, y-координаты и z-координаты, после чего суммируем полученные значения.

3*1 + 0*3 + -4*4 = -13

Вычисляем корень квадратный из суммы 3*3 + 0*0 + (-4)*(-4) = 9 + 16 = 25. Он равняется 5.

Вычисляем корень квадратный из суммы 1*1 + 3*3 + (4)*(4) = 1 + 9 + 16 = 26. Он равен 5,09.

Перемножаем полученные значения, 5 * 5,09. В итоге с допустимой погрешностью получится 25.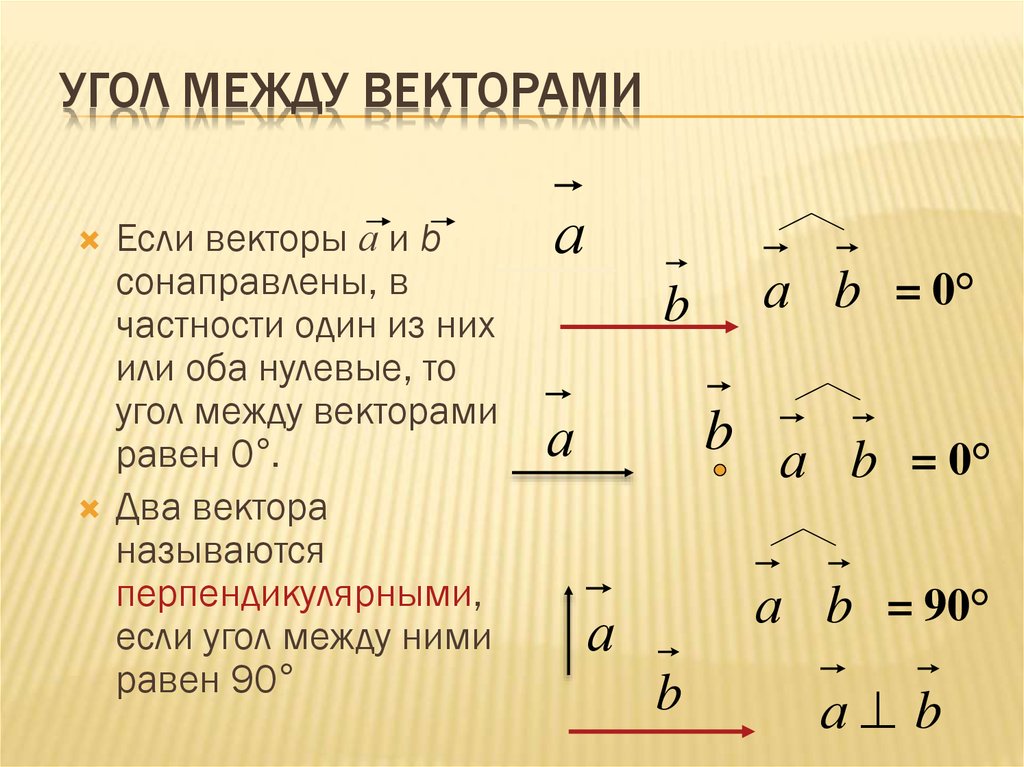

Далее нам нужно -13 поделить на 25. Результат вычисления равен -0,52. После округления до первого знака после запятой будем иметь -0,5.

Arccos (-1/2) равен 120 градусам.

Теперь попытаемся получить тот же результат с помощью вычисления угла по скалярному произведению векторов.

Сначала вычисляем длину каждого из векторов.

3*3 + 0*0 + (-4)*(-4) = 9 + 16 = 25.
1*1 + 3*3 + (4)*(4) = 1 + 9 + 16 = 26.

Далее находим корни из этих чисел.

В нашем случае, несмотря на то что координаты каждого из векторов абсолютно разные, длина их получилась примерно одинаковой: 5 и 5,09. Последнее число, как мы делали выше, лучше округлить.

Далее вычисляем скалярное произведение
3*1 + 0*3 + -4*4 = -13
Как и ранее, делим -13 на 25. С допустимой погрешностью получаем значение (-1/2). Опять вычисляем арккосинус из этого числа. Он будет 120 градусов.
Ответ: Угол между векторами a = (3, 0, -4) и b = (1, 3, 4) равен 120 градусам.
Не редко встречаются задачи, в которых в прямоугольной декартовой системе координат заданы координаты трёх точек и нужно выяснить, чему равняется какой-нибудь угол. Для этого определяют угол между векторами, концами которых являются координаты этих точек.
Пример 3. На плоскости дана прямоугольная система координат, а на ней заданы точки A(2,-1), B(3,2), С (7,-2). Требуется найти косинус угла, разделяющего векторы
AB и BC.
Находим координаты векторов.
Для AС x = x₂-x₁= 7-2 =5, y = y₂-y₁ = -2 – (-1) = -1, т. е. получаем вектор AС (5, -1).
Для ВС x = 7-3 =4, y = -2 – (-2) = -4, т. е. получаем вектор BC (4, -4).
Теперь, воспользовавшись соответствующей формулой, определим угол между векторами на плоскости.
cos (a, b) = (a, b)/(a*b)
Сначала вычисляем скалярное произведение AB и BC.
Затем корни из 5*5 + (-1)*(-1) и из 4*4 + (-4)*(-4).
Делим одно на другое.
Косинус в этом примере будет равен 0,832 (если более точно, то 3 делённое на 13 в корне).

Ответ: Искомый косинус угла равен 0,832.
Помимо сказанного, угол между векторами можно также определить по теореме косинусов. Отложите от точки 0 векторы OA = a и OB = b. Будет треугольник OAB. По теореме косинусов будет справедливо следующее равенство
AB²= OA²+ OB² – 2*OA*OB* cos (AOB)
Это равносильно
(b –a)²= a+ b – 2*a*b*cos (a,b)
Отсюда легко вывести формулу косинуса угла.
Нужно сначала перенести 2*a*b*cos (a,b) в левую сторону, затем (b –a)²в правую и всё поделить на 2.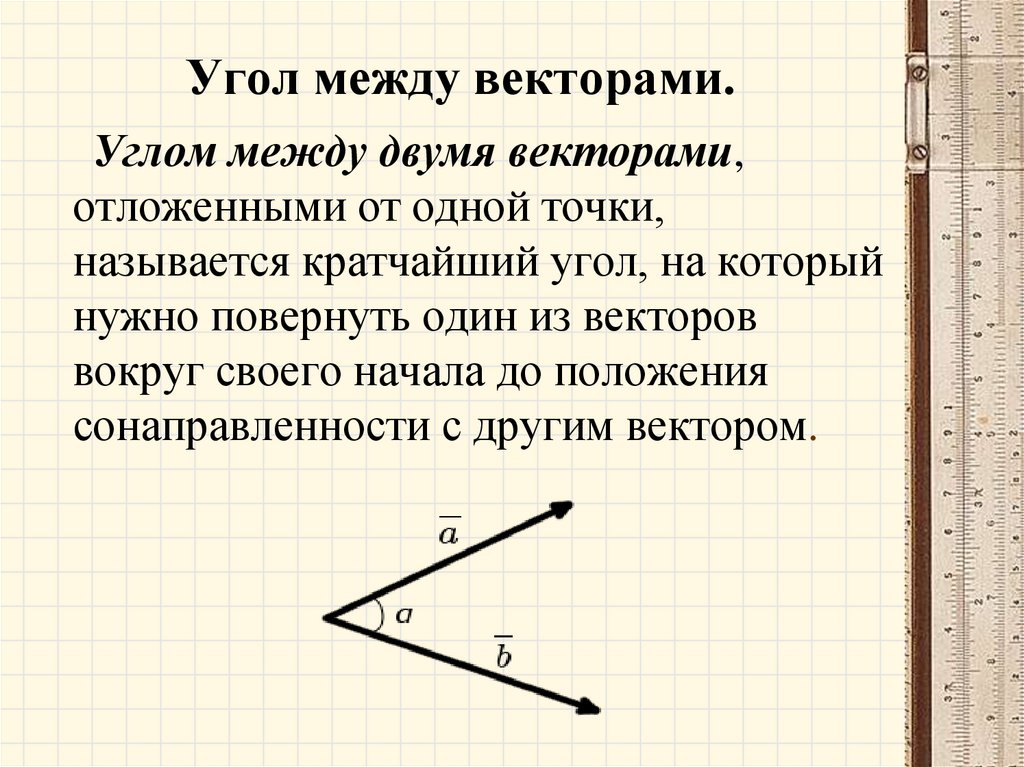
В результате будем иметь
cos(a,b) = (a + b)/ 2*a*b
Чтобы использовать полученные формулы, нам нужно знать длины векторов, но это не проблема, т. к. по координатам они определяются очень легко.
Несмотря на то что указанный способ известен почти всем, чаще всего используется формула
cos(a,b) = (a,b)/a*b
Попробуйте и то, и другое. С теми формулами и способами, которыми вам будет удобнее, с теми и работайте. Для полного освоения темы в начале советуем натренироваться в решении задач всеми указанными в статье методами. Только после этого решайте, что для вас предпочтительнее и лучше идёт.
Калькулятор вычисления угла между векторами
Угол между векторами
Урок 27. Геометрия 9 класс ФГОС
Данный материал знакомит учащихся с углом между векторами, а также правилами его обозначения и построения на плоскости.
В уроке рассмотрены частные случаи расположения векторов и величины углов между ними. Большое количество разнообразных задач помогает усвоению и закреплению данного материала.

Конспект урока «Угол между векторами»
Изобразим произвольные векторы и .
Далее от некоторой точки О отложим векторы и , равные векторам и
соответственно. Тогда угол АОB будет являться углом между векторами и .
Обозначим градусную меру угла АОB за α.
Говорят, что угол между векторами и равен α.
Если выбрать некоторую точку О₁ и отложить от неё векторы и , равные соответственно векторам и , то полученный угол А₁О₁B₁ будет равен углу АОB. Значит, и их градусные меры тоже равны.
Отсюда можем сделать вывод, что величина α не зависит от выбора точки, от которой будут отложены векторы.

Угол между векторами и будем обозначать так.
Величина его равна α.
Например, угол между векторами и равен 25°. Угол между векторами и — 70°. Угол между векторами и равен 110°.
Далее рассмотрим несколько частных случаев.
Первой будет пара коллинеарных сонаправленных векторов. Видим, что угол между ними равен нулю.
Так же угол между векторами равен 0, если один из них является нулевым или оба вектора нулевые. Ведь нулевой вектор сонаправлен любому, а значит, эти случаи можно отнести к первому, где рассматривались сонаправленные векторы.
Теперь рассмотрим пару противоположно направленных векторов, отложенных от одной точки.
Видим, что угол между ними равен 180°.
Ещё одним частным случаем являются векторы, угол между которыми равен 90°. Такие векторы называют перпендикулярными.
Ранее мы с вами рассматривали также углы между прямыми. Вы должны помнить, что они всегда были острыми.
В случае с векторами, угол между ними может быть как острым, так и тупым, но не больше 180°.
Можно записать, что величина угла между векторами .
Задача. равносторонний. Найти:
а) , ;                        б) , ;                       в) , .
Решение.
а)

б)

в)

Выполнив это задание, мы убедились в том, что угол между векторами лежит в пределах от 0 до 180° в отличие от угла между двумя прямыми.
Задача.
Среди векторов , , , , , указать пары перпендикулярных векторов, лежащих в одной грани прямоугольного параллелепипеда .
1)
2)
3)
4)
5)
Далее решим задачу.
Задача. Меньшая диагональ ромба равна его стороне. Найти:
а)         б)         в)         г)         д)         е)
Решение.
а)
б)
в)
г)
д)
е)
Задача. В , , . Найти .
Решение.
По теореме косинусов:
,


Ответ: .
Можем подвести итоги урока.
Сегодня мы говорили об угле между двумя векторами. И выяснили, что он в отличии от угла между прямыми может быть и тупым. Но изменяется такой угол в пределах от 0 до 180°.

Причем величина угла не зависит от выбора точки, от которой будут отложены векторы.
Среди частных случаев мы выделили угол между сонаправленными векторами. Он равен нулю.
Так же нулю равен угол между векторами, если хотя бы один из них является нулевым вектором.
Ещё мы отметили, что угол между противоположно направленными векторами равен 180°.
Если же угол между векторами равен 90°, то такие векторы называют перпендикулярными.
Все эти сведения помогли нам успешно справиться с решением задач.

Предыдущий урок 26 Измерительные работы
Следующий урок 28 Скалярное произведение векторов

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Угол между векторами — Понятие
Векторная формула для нахождения угла между векторами полезна для запоминания. Эта формула использует скалярное произведение, величину и косинус, чтобы дать нам угол между векторами. Мы можем использовать эту формулу не только для нахождения угла между векторами , но также для нахождения угла между плоскостями и угла между векторами в пространстве или в трехмерной системе координат.
скалярное произведение угол между векторами векторы положения
Я хочу поговорить об очень важном свойстве скалярного произведения, которое можно использовать для нахождения угла между двумя векторами, поэтому, скажем, у нас есть два вектора u и v, вот угол между ними, и это будет некоторый угол. между 0 и пи, и если я хочу найти его, я могу использовать это свойство скалярного произведения. Косинус теты равен скалярному произведению двух векторов, деленному на произведение их величин, помните, что тета всегда будет между 0 и пи или 0 градусов и 180.
Давайте посмотрим, как это работает, вот пример: пусть u равно 3 минус 1, а v равно 2 минус 5.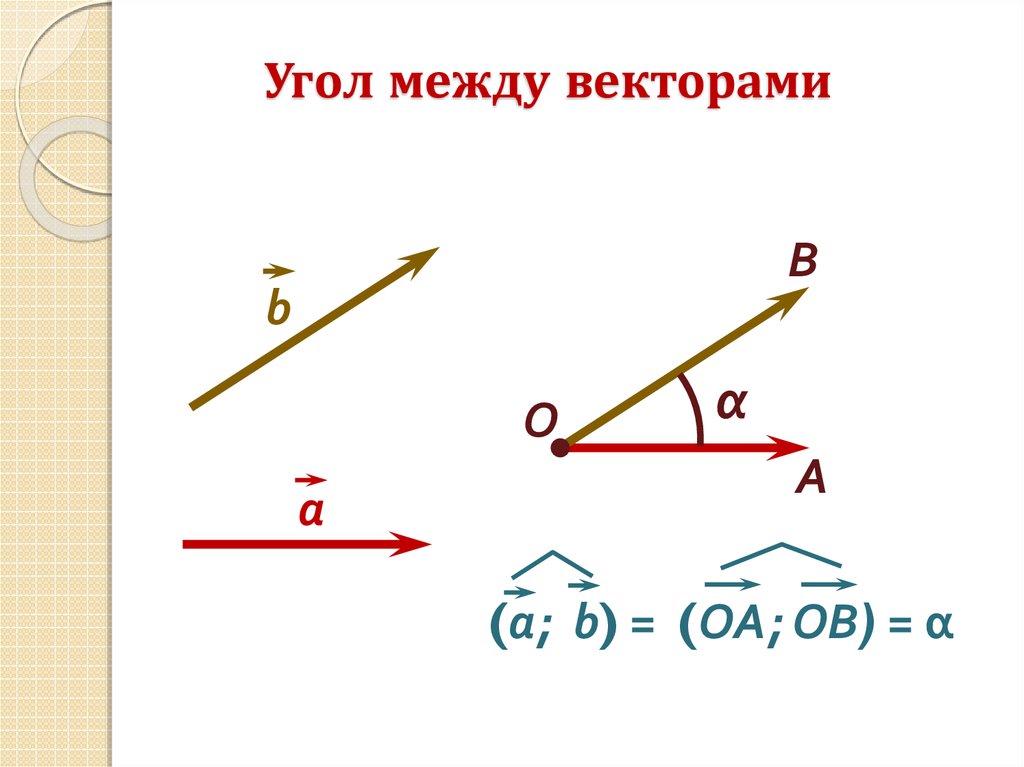 Позвольте мне сначала набросать это как векторы положения, а затем я вычислю угол между ними. Теперь вспомните, что когда вы рисуете вектор как вектор положения, вы помещаете его начальную точку в начало координат, поэтому 3 минус 1 будет конечной точкой. 3 отрицательных 1 здесь, поэтому мой вектор u находится прямо здесь, так что это его вектор положения, я назову его u, а затем v переходит от начала координат к 2 отрицательным 5, 2, 1, 2, 3, 4, 5, так что что-то вроде этот момент здесь и сейчас, рисуя их заранее, дает нам некоторое представление о том, чего ожидать от угла между ними. Это v, угол между ними выглядит как q, так что лучше знать заранее.
Давайте вычислим его, используя эту формулу. Косинус тета равен точечному произведению двух векторов u.v на произведение их величин. Итак, я должен вычислить их величины, теперь величина u равна квадратному корню из 3 в квадрате плюс минус 1 в квадрате. Квадратный корень из 9 плюс 1 корень из 10 и величина v — это квадратный корень из 2 в квадрате или 4 плюс минус 5 в квадрате или 25, и это дает 29. Итак, я могу записать косинус тета равный в корень знаменателя 10 раз корень 29 хорошо, теперь давайте посчитаем скалярное произведение u.v это 3 умножить на 2, 6 плюс минус 1 умножить на минус 5, 5. Итак, мы получаем 11 над этим произведением квадратных корней, я напишу это как квадратный корень из 290 быстрее ввести в калькулятор и это косинус тета. Поэтому, если я хочу тета, нам нужно использовать арккосинус, тета будет равна арккосинусу 11 относительно корня 290. Итак, давайте вычислим это, и я хотел бы, чтобы мой ответ был в градусах, поэтому я собираюсь убедиться, что я нахожусь в градусный режим и я. Таким образом, арккосинус 11, деленный на квадратный корень из 290, равен 49,8 градусам, это приблизительное значение, и оно выглядит примерно так.
Так что помните, когда вы вычисляете угол между двумя векторами, используйте эту формулу, очень важную, очень важную в применении скалярного произведения. Косинус угла между двумя векторами равен скалярному произведению двух векторов, деленному на произведение их величин.
Угол между двумя векторами — объяснение, пример решения и часто задаваемые вопросы
Геометрия — одна из тем, которые нравятся многим учащимся, независимо от того, любят ли они расчеты. Построение углов с помощью масштаба и циркуля дает нам другую радость и отдых в мире чисел и таблиц умножения. Но затем приходит тригонометрия, чтобы добавить немного сложности, и вместе с тригонометрией вы впервые почувствуете вкус векторов.
Да, векторы также являются частью математики и геометрии. Угол между двумя векторами — это наименьший угол, на который можно повернуть один вектор вокруг своей оси так, чтобы он выровнялся с другим вектором. Два вектора необходимы для получения скалярной величины, которая, как говорят, является действительным числом.
Сегодня мы попытаемся найти угол между двумя векторами, используя тригонометрические формулы. Мы сделаем это так, чтобы ученикам было легче понять.
(Изображение скоро будет обновлено)
(Два вектора, соединенные через точки, образующие угол тета. )
Если вы хотите найти угол между двумя векторами с помощью калькулятора, вас может ждать сюрприз. Тем не менее, в Интернете есть много веб-сайтов, которые могут показать вам прямой ответ, но это не то, как вы будете получать оценки на экзаменах. Так что будем помогать решать.
Угол между двумя векторами Формула
Чтобы найти угол между векторами, нам сначала нужно взять в уравнении два вектора. Предположим, что есть два вектора, и назовем их вектор (X) и вектор (Y). Теперь разделите эти два вектора углом.
Здесь мы создали ситуацию, которая поможет нам найти угол между двумя векторами. Чтобы узнать угол, нам сначала нужно узнать скалярное произведение заданных векторов. В результате вектор (X) и вектор (Y) = |X| |Y| Кос 9{-1}\frac{\overrightarrow{x}.\overrightarrow{y}}{|\overrightarrow{x}||\overrightarrow{y}|}\]
В приведенном выше уравнении мы можем найти угол между два вектора.
Это был простой способ найти угол между двумя векторами. Давайте теперь пройдемся по двум распространенным способам определения этого угла, а затем решим, какой из них использовать для нашего случая.
Два метода расчета угла между двумя векторами
Существуют две основные формулы, которые обычно используются для определения угла между двумя векторами: одна в терминах скалярного произведения, а другая в терминах перекрестного произведения. Однако наиболее широко используемая формула для определения угла между двумя векторами включает метод скалярного произведения. Теперь мы увидим, какая проблема возникает, когда мы используем метод перекрестного произведения. Рассмотрим x и y как два вектора, а θ как угол между ними. Ниже приведены две формулы, которые можно использовать для нахождения угла между ними. В этих формулах используется как скалярное произведение, так и перекрестное произведение. 9{-1} [ \frac{x \times y}{ \left | х \ справа | \влево | у \право |}\].
Здесь x · y — скалярное произведение, а x × y — перекрестное произведение x и y. Следует отметить, что формула перекрестного произведения требует величины числителя, а формула скалярного произведения — нет.
Примечание. Когда дело доходит до определения угла между двумя равными векторами, вам не нужно решать какое-либо уравнение, так как угол будет равен нулю. Основная причина этого заключается в том, что два равных вектора будут иметь одинаковое направление и величину.
Решенный пример
Попробуем использовать следующее уравнение для определения угла между двумя векторами 3i + 4j — k и 2i — j + k.
Первый вектор равен 3i + 4j — k.
Второй вектор равен 2i — j + k.
Теперь давайте найдем скалярное произведение этих двух.
= (3i + 4j — k ).(2i — j + k).
= (3)(2) + (4)(-1) + (-1)(1)
= (6-4-1)
= -1
Таким образом, скалярное произведение двух векторов = 1,
9{-1} (0,0802)\]
= 85,39 ^o
Заключение
Подводя итог, давайте рассмотрим основные моменты, которые мы узнали по этой теме.
No related posts.