Стереометрия. Геометрия в пространстве
Стереометрия. Геометрия в пространстве
ОглавлениеПРЕДИСЛОВИЕ К ЧИТАТЕЛЮВВЕДЕНИЕ ГЛАВА 1. ПРЯМЫЕ И ПЛОСКОСТИ § 1.  ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ И ПЛОСКОСТЕЙ1.3. Плоскость и прямая в пространстве. 1.4. Аксиомы стереометрии. 1.5. Взаимное расположение двух прямых в пространстве. 1.6. Признаки скрещивающихся прямых. 1.7. Параллельные прямые. 1.8. Параллельное проектирование. § 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 2.2. О значении перпендикуляра. 2.3. Теорема о трех перпендикулярах. 2.4. Признак перпендикулярности прямой и плоскости. 2.5. Построение плоскости, перпендикулярной данной прямой. 2.6. Связь между параллельностью прямых и перпендикулярностью прямой и плоскости. 2.7. Теорема о прямой, перпендикулярной плоскости. 2.8. Перпендикулярность плоскостей. 2.9. Ортогональное проектирование. § 3. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ 3.2. Параллельность и перпендикулярность. 3.3. Основная теорема о параллельных плоскостях. 3.4. Второй признак параллельности плоскостей. 3.5.  Расстояние и параллельность.3.6. Сонаправленность лучей и угол между прямыми. 3.7. Параллельность и углы. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 2. ВАЖНЕЙШИЕ ПРОСТРАНСТВЕННЫЕ ФИГУРЫ § 4. СФЕРА И ШАР 4.2. Взаимное положение шара и плоскости. 4.3. Сфера и многранники. 4.4. Вид и изображение шара и сферы. 4.5. Опорная плоскость. 4.6. Ограниченные фигуры. Диаметр фигуры. 4.7. Опорные плоскости в концах диаметра. 4.8. Сфера — фигура вращения. 4.9. Симметрия сферы и шара. 4.10. Сфера — центрально симметричная фигура. 4.11. Сфера — зеркально симметричная фигура. 4.12. Отражение в плоскости и отражение в зеркале. § 5. ТРЕХГРАННЫЕ УГЛЫ И СФЕРИЧЕСКИЕ ТРЕУГОЛЬНИКИ 5.2. Тригонометрия трехгранного угла. 5.3. Равенство трехгранных углов. 5.4. Сферические треугольники. 5.5. “Неравенство треугольника” для трехгранных углов и сферических треугольников. 6.2. Другой подход к определению цилиндра.  6.3. Цилиндр вращения. 6.4. Эллипс как сечение цилиндра вращения. 6.5. Винтовые линии. 6.6. Цилиндры в практике. § 7. ПРИЗМА 7.2. Параллелепипед. 7.3. Прямоугольный параллелепипед. 7.4. Симметрия параллелепипеда. 7.5. Симметрия правильных призм. Поворот вокруг прямой. § 8. КОНУС 8.2. Сечение конуса плоскостью, параллельной плоскости основания. 8.3. Конус вращения. 8.4. Усеченный конус. § 9. ПИРАМИДА 9.2. Правильная пирамида. 9.3. Симметрия правильной пирамиды. 9.4. Конусы и пирамиды в практике. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 3. ТЕЛА, ПОВЕРХНОСТИ, МНОГОГРАННИКИ § 10. ТЕЛА И ИХ ПОВЕРХНОСТИ 10.2. Граница и внутренность. 10.3. Определение тела и замкнутой плоской области. 10.4. Выпуклые фигуры. 10.5. Выпуклые тела. § 11. МНОГОГРАННИКИ 11.2. Выпуклые многогранники. 11.3. Теорема Эйлера. 11.4. Выпуклые многогранники и выпуклые оболочки. 11.5. Многогранная поверхность и развертка.  11.6. Развертка выпуклого многогранника. § 12. ПРАВИЛЬНЫЕ И ПОЛУПРАВИЛЬНЫЕ МНОГОГРАННИКИ 12.2. Классификация правильных многогранников. 12.3. Полуправильные многогранники. 12.4. Симметрия правильных многогранников. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 4. ОБЪЕМЫ ТЕЛ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ § 13. ПОНЯТИЕ ОБЪЕМА 13.2. Определение объема. 13.3. Геометрические величины. § 14. ОБЪЕМ ПРЯМОГО ЦИЛИНДРА 14.2. Объем прямой призмы. § 15. ПРЕДСТАВЛЕНИЕ ОБЪЕМА ИНТЕГРАЛОМ 15.2. Выражение объема через площади сечений. § 16. ОБЪЕМ ЦИЛИНДРА, КОНУСА, ШАРА 16.2. Объем конуса 16.4. Объем тел вращения. 16.5. Объем шарового сегмента и шарового сектора. § 17. ПЛОЩАДЬ ПОВЕРХНОСТИ 17.2. Площадь сферы. 17.3. Площадь сферических многоугольников. 17.4. Площадь сферического сегмента и сферического пояса. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 5.  КООРДИНАТЫ И ВЕКТОРЫ§ 18. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ 18.2. Другой способ нахождения координат точки. 18.3. Построение точки с данными координатами. 18.4. Выражение расстояния между точками. § 19. МЕТОД КООРДИНАТ 19.2. Уравнения без одной или двух координат. 19.3. Некоторые применения метода координат. § 20. РАЗЛИЧНЫЕ СИСТЕМЫ КООРДИНАТ 20.2. Полярные координаты. 20.3. Цилиндрические координаты. 20.4. Сферические координаты. 20.5. Координатная сеть. § 21. ПОНЯТИЕ ВЕКТОРА 21.2. Параллельность (коллинеарность) и перпендикулярность (ортогональность) векторов. 21.3. Сонаправленность и равенство векторов. 21.4. Признаки равенства векторов. 21.5. Радиус-вектор. § 22. ЛИНЕЙНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ 22.2. Разложение вектора на составляющие. 22.3. Умножение вектора на число. 22.4. Координаты вектора. 22.5. Равенство координат векторов и координат точек. 22.6. Разложение векторов по базису. 22.7. Ориентация базиса.  § 23. СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ 23.2. Выражение скалярного произведения через координаты. 23.3. Свойства скалярного умножения. 23.4. Применения скалярного умножения. 23.5. Скалярное произведение и проекции. § 24. ВЕКТОРНЫЙ МЕТОД 24.2. Общее уравнение плоскости. 24.3. Векторное задание отрезка. 24.4. Некоторые теоремы о треугольниках и тетраэдрах. 24.5. Центр масс системы материальных точек. 24.6. Центры масс и выпуклые многогранники. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ГЛАВА 6. ПРЕОБРАЗОВАНИЯ 25.1. Преобразования фигур. 25.2. Определения движения и равенства фигур. 25.3. Преобразования симметрии. 25.4. Параллельный перенос. 25.5. Поворот. § 26. СВОЙСТВА ДВИЖЕНИЙ 26.2. Общие свойства движений. 26.3. Теоремы о задании движений. 26.4. Неподвижные точки движений. 26.5. Два рода движений. 26.6. Теорема подвижности пространства. 26.7. Композиция отражений в плоскости.  § 27. КЛАССИФИКАЦИЯ ДВИЖЕНИЙ ПРОСТРАНСТВА 27.2. Движения первого рода как винтовые движения. 27.3. Движение второго рода, имеющее неподвижную точку, как зеркальный поворот. 27.4. Движения второго рода, не имеющие неподвижных точек, как скользящие отражения. § 28. ПОДОБИЕ 28.2. Гомотетия. 28.3. Свойства подобия. 28.4. Группы преобразований. § 29. ИНВЕРСИЯ 29.2. Аналитическое задание инверсии. 29.3. Образы прямых и окружностей, плоскостей и сфер при инверсии. 29.4. Сохранение величин углов при инверсии. ЗАДАЧИ С РЕШЕНИЯМИ ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ОТВЕТЫ И УКАЗАНИЯ ОСНОВНЫЕ ТЕОРЕМЫ И ФОРМУЛЫ ПЛАНИМЕТРИИ |
Выпуклая фигура — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Доказать, что в симметрической выпуклой фигуре диаметр проходит через центр симметрии. [31]
Докажите, что крут — выпуклая фигура.
[32]
Строгое определение понятий фигура и выпуклая фигура приведено в гл. [33]
Областью решений системы неравенств является неограниченная выпуклая фигура. [34]
Легко видеть, что точка выпуклой фигуры Е, принадлежащая опорной гиперплоскости, всегда является для Е граничной точкой. [35]
Рассмотрим точку Р на границе выпуклой фигуры Q ( черт. [36]
Самыми простыми ( плоскими) выпуклыми фигурами являются выпуклые многоугольники; при этом очень важной является возможность заменить произвольную плоскую выпуклую фигуру F сколь угодно близким к нейъ выпуклым многоугольником М, например, вписанным в F. Выделенное курсивом свойство вы пуклых многоугольников позволяет считать их, в каком-то смысле, самыми главными ( плоскими) выпуклыми фигурами — очень многие свойства выпуклых многоугольников удается затем автоматически перенести на все выпуклые фигуры основываясь на этой возможности приблизить каждую выпуклую фигуру выпуклыми многоугольниками.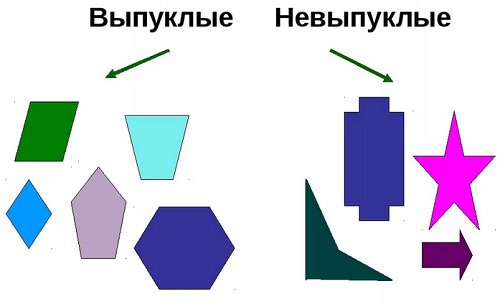
Это обстоятельство делает соблазнительной попытку изложения некоторой части общей теории выпуклых фигур на ( доступном и привычном школьникам. Настоящий сборник задач ни в какой мере не претендует, конечно, на решение столь общей методической задачи; однако нам хочется порекомендовать читателям продумать вопрос о возможности переноса тех или иных результатов собранных в цикле 4 задач на ( произвольные.
[37]
| Парадокс шара, получаем радиус внутрен. [38] |
Шары, конечно, являются выпуклыми фигурами, расстояние — правильным Евклидовым расстоянием, радиусы угловых шаров равны, конечно, единице, так что сделанный вывод неизбежен. При п — 10 внутренний шар вылезает за пределы куба, что противоречит всем обычным представлениям. [39]
Докажите, что полуплоскость является выпуклой фигурой. [40]
Напомним, что — мерный симплекс-это выпуклая фигура с k — — линейно независимыми вершинами, и что его можно ориентировать ровно двумя способами, фиксируя порядок вершин с точностью до четной перестановки.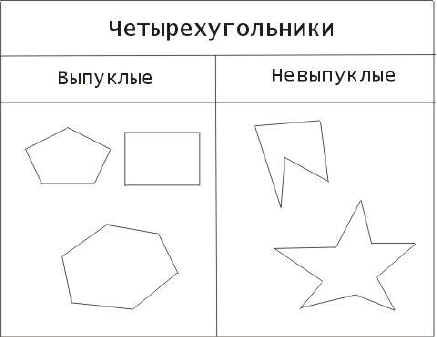
Легко проверить, что Е — выпуклая фигура, для которой Q служит калибровочной функцией. [42]
Областью решений данной системы неравенств является неограниченная выпуклая фигура. [43]
Минковский доказал следующую тоорему: Если выпуклая фигура Q ( плоская или трехмерная) разбита на конечное число центрально-симметрических частей, то Q обладает центром симметрии. [44]
Круг, полукруг, эллипс являются выпуклыми фигурами. Среди четырехугольников встречаются как выпуклые ( например, параллелограмм), так и невыпуклые ( черт. Круговой сектор является выпуклой фигурой, если его центральный угол меньше ir ( 180), и невыпуклой, — если его центральный угол больше тт. [45]
Страницы: 1 2 3 4
Выпуклая форма | Определение | Решенные примеры
Содержание 1.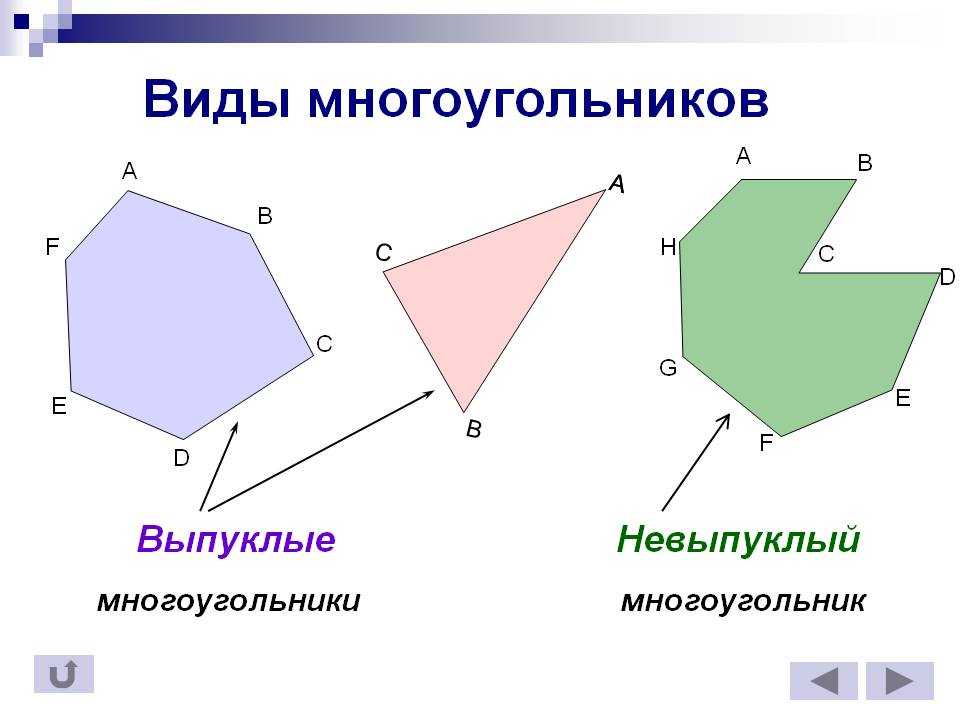 | Выпуклое определение |
| 2. | Выпуклый многоугольник |
| 3. | Вогнутое определение |
| 4. | Различия между выпуклыми и вогнутыми формами (с иллюстрацией) |
| 5. | Нестандартное мышление! |
| 6. | Решенные примеры на выпуклых формах |
| 7. | Важные замечания по выпуклым формам |
| 8. | Практические вопросы по выпуклым фигурам |
| 9. | Образцы заданий олимпиады по математике |
| 10. | Часто задаваемые вопросы (FAQ) |
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на «почему», стоящем за «что». Учащиеся могут изучить огромное количество интерактивных рабочих листов, визуальных материалов, симуляций, практических тестов и многого другого, чтобы глубже понять концепцию.
Запишитесь на БЕСПЛАТНОЕ пробное занятие сегодня! и участвуйте в LIVE онлайн-классе Cuemath вместе со своим ребенком.
Выпуклое определениеВыпуклая форма — это форма, все части которой «направлены наружу».
Другими словами, никакая его часть не указывает внутрь.
Например, полная пицца имеет выпуклую форму, поскольку ее полный контур (окружность) направлен наружу.
Некоторые другие выпуклые формы:
Определение выпуклости в геометрииВыпуклая форма в геометрии — это форма, в которой линия, соединяющая каждые две точки фигуры, полностью лежит внутри фигуры.
Выпуклая линзаВыпуклая линза, как следует из названия, направлена наружу.
Выпуклая линза также известна как «собирающая линза».
Выпуклый многоугольник
Выпуклый многоугольник можно определить тремя способами.
\circ\). 9\цирк\)
Вогнутое определение
Вогнутая форма — это форма, по крайней мере некоторая часть которой «указывает внутрь».
Если мы удалим кусок пиццы, он будет выглядеть так:
На изображении некоторые части контура пиццы направлены внутрь.
Следовательно, это вогнутая форма.
Некоторые другие примеры вогнутых форм:
CLUEless по математике? Посмотрите, как CUEMATH Учителя объяснят вашему ребенку Выпуклые фигуры с помощью интерактивных симуляций и рабочих листов, чтобы им больше никогда не приходилось запоминать что-либо по математике!
Исследуйте живые, интерактивные и персонализированные онлайн-классы Cuemath, чтобы ваш ребенок стал экспертом по математике. Запишитесь на БЕСПЛАТНОЕ пробное занятие сегодня!
Различия между выпуклыми и вогнутыми формами (с иллюстрациями)
Различия между выпуклыми и вогнутыми формами заключаются в следующем.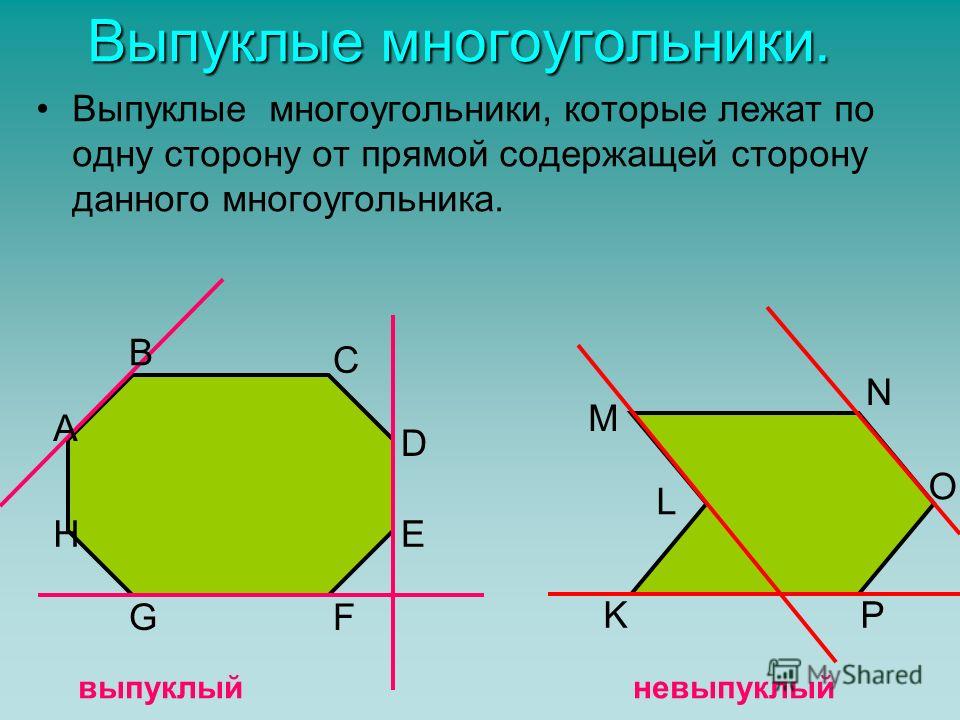
| Выпуклые формы | Вогнутые формы |
|---|---|
Полный контур выпуклой формы направлен наружу. то есть вмятин нет. Пример: | По крайней мере, часть вогнутой формы направлена наружу, т. е. имеется вмятина. 9\круг\). Пример вогнутого восьмиугольника: |
Прямая, соединяющая любые две точки выпуклой фигуры, целиком лежит в ней. | Линия, соединяющая любые две точки вогнутой формы, может лежать в ней, а может и не лежать. |
Вы можете определить разницу между выпуклой и вогнутой формами, используя следующую иллюстрацию.
Здесь вы можете перетаскивать вершины любого многоугольника и смотреть, как он меняется от «выпуклого к вогнутому» или наоборот.
Think Tank
- Является ли сумма внутренних углов вогнутого многоугольника \(n\) сторон \(180(n-2)\) градусов?
- Является ли сумма внешних углов вогнутого многоугольника \(n\) сторон \(360\) градусов?
Помогите своему ребенку получить более высокие баллы с помощью собственного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Проведите тест сейчас.
Решенные примеры
| Пример 1 |
Чему равен внутренний угол правильного пятиугольника?
Решение:
Количество сторон пятиугольника равно \(n=5\)
Мы знаем, что сумма всех внутренних углов многоугольника \(n \) сторон равна \(180( п-2)\) градусов.
\circ\). 9\круг\).
Математическая Олимпиада Образцы. Это побуждает детей развивать свои навыки решения математических задач с точки зрения конкуренции.
Вы можете скачать БЕСПЛАТНЫЕ образцы работ по классам ниже:
- Образец бумаги ИМО класса 1
- Образец бумаги IMO класса 2
- Образец бумаги IMO класса 3
- Образец бумаги IMO Class 4
- Образец бумаги IMO Class 5
- Образец бумаги IMO Class 6
- Образец бумаги IMO класса 7
- Образец бумаги IMO Class 8
- Образец бумаги IMO класса 9
- Образец бумаги IMO Class 10
Узнать больше об олимпиаде по математике можно нажмите здесь
Часто задаваемые вопросы (FAQ)
1. Что такое выпуклое множество? Приведите пример.
Выпуклое множество — это множество, в котором прямая, соединяющая любые две точки \(A\) и \(B\) этого множества, полностью принадлежит ему.
Пример. Множество действительных чисел \(R\) является выпуклым множеством.
2. Что такое выпуклая форма?
Выпуклая фигура — это фигура, все части которой «направлены наружу».
Другими словами, никакая его часть не указывает внутрь.
Для получения более подробной информации вы можете обратиться к разделу «Определение выпуклости» на этой странице.
Выпуклые и вогнутые многоугольники – определение, различия, примеры
В зависимости от внутренних углов все многоугольники можно разделить на две группы: выпуклые и вогнутые.
Выпуклые и вогнутые многоугольникиЧто такое выпуклый многоугольник
Выпуклый многоугольник — это многоугольник, все внутренние углы которого меньше 180°. Все диагонали выпуклого многоугольника лежат внутри замкнутой фигуры. Выпуклый многоугольник может быть как правильным, так и неправильным.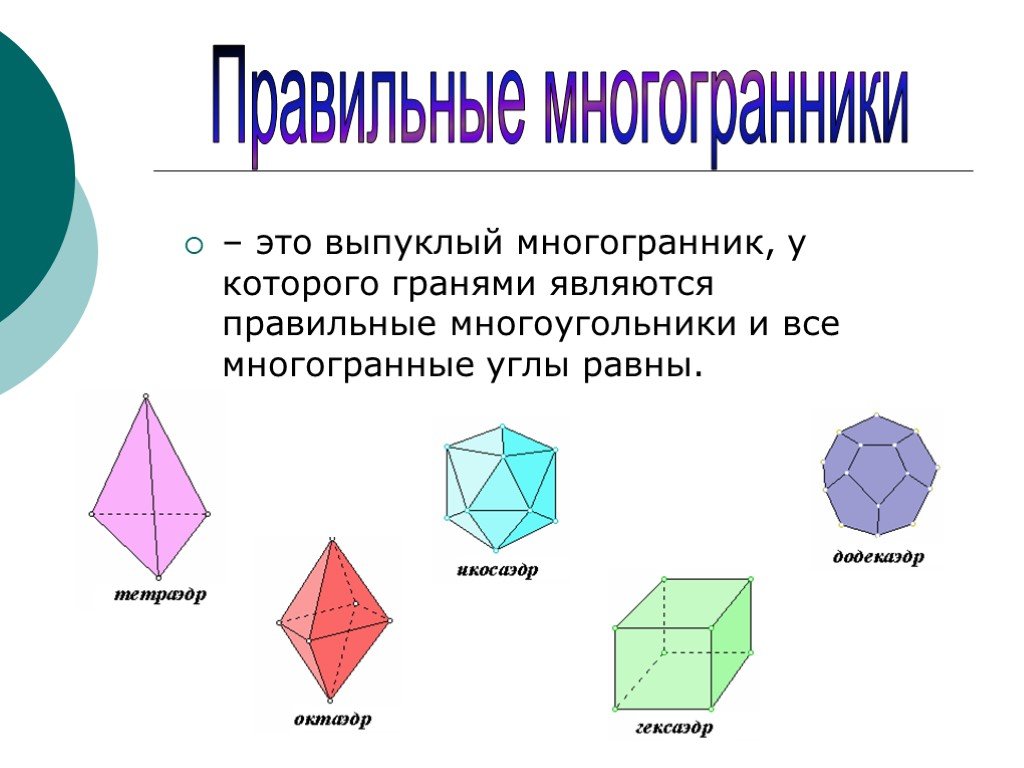
Правильные выпуклые многоугольники имеют все стороны одинаковой длины и все внутренние углы одинаковой величины (меньше 180°). Выпуклые многоугольники, которые не являются правильными, называются неправильными выпуклыми многоугольниками.
Примеры : Треугольники, все выпуклые четырехугольники, правильный пятиугольник и правильный шестиугольник — все это выпуклые многоугольники. Квадрат – это правильный выпуклый многоугольник.
Выпуклый многоугольникСвойства
- Все внутренние углы меньше 180°; ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA и ∠FAB меньше 180°
- Все девять диагоналей лежат внутри замкнутой фигуры; диагонали AC, AD, AE, BD, BE, BF, CE, CF и CA лежат внутри фигуры.
- Сумма всех внешних углов равна 360°
- Сумма всех внутренних углов, имеющих n -сторон, равна ( n – 2) x 180°
В данном пятиугольнике ABCDE все внутренние углы равны. Укажите, является ли он выпуклым многоугольником.
Решение:
Как мы знаем,
Внутренний угол правильного многоугольника = (n-2) × 180°/n, здесь n = 5
= (5-2) x 180°/5
= 3 x 180° /5
= 108°
Поскольку все пять внутренних углов в данном пятиугольнике меньше 180°, это выпуклый многоугольник.
Формулы
Площадь
Это общее пространство внутри полигона. The formula is given below:
Area ( A ) = ½|(x 1 y 2 – x 2 y 1 )+(x 2 y 3 – x 3 у 2 )+……..+(х н у 1 – х 1 у н )|, здесь (х 1 , у 1 , у 2 ), (х 3 , у 3 ),…….., (х n , y n ) — вершины многоугольника на координатной плоскости )
Solution:
As we know,
Area (A) = ½|(x 1 y 2 – x 2 y 1 )+(x 2 y 3 – x 3 y 2 )+(x 3 y 1 – x 1 y 3 )|,
здесь (x 1 , у 1 ) = (5, 2), (х 2 , у 2 ) = (12, 8), (х 3 , у 3 ) = (5, — 2)
= ½|(40-24)+ (-24-40)+ (10)-10)|
= ½|16-64|
= 48/2
Внутренние углы
Внутренние углы многоугольника — это углы внутри многоугольника.
У многоугольника столько же внутренних углов, сколько и сторон.
Сумма внутренних углов
Это общая мера всех внутренних углов, объединенных в многоугольнике. Формула для определения суммы всех углов любого выпуклого правильного многоугольника приведена ниже:
Сумма внутренних углов = ( n -2) × 180°, здесь n = общее количество сторон многоугольника выпуклый правильный многоугольник.
Решение:
Как известно,
Сумма внутренних углов = (n-2) × 180°, здесь n = 22
= (14-2) x 180°
= 2160°
Один внутренний угол
Каждый внутренний угол имеет одинаковые размеры в правильном выпуклом многоугольнике и может быть получен путем деления суммы внутренних углов на общее количество сторон. Формула приведена ниже:
Внутренний угол выпуклого многоугольника = ( n -2) × 180° / n , здесь n = общее количество сторон многоугольника
Найти меру внутренних углов выпуклый правильный многоугольник с 12 сторонами.
Решение:
Как мы знаем,
Внутренний угол правильного многоугольника = (n-2) × 180°/n, здесь n = 18
= (18-2) x 180°/18
= 16 x 180° /18
= 160°
Наружные углы
Внешний угол многоугольника — это угол, образованный одной стороной и продолжением соседней стороны.
Теорема о сумме внешних углов утверждает, что сумма внешних углов любого выпуклого многоугольника равна 360°. Для правильных выпуклых многоугольников с n сторонами каждый внешний угол определяется по следующей формуле:
Внешний угол выпуклого правильного многоугольника = 360°/ n , здесь n = общее количество сторон многоугольника
Вычислите внешний угол в 15-стороннем правильном выпуклом многоугольнике.
Решение:
Как известно,
Внешний угол правильного многоугольника = 360°/n, здесь n =15
= 360°/15
= 24°
Что такое вогнутый многоугольник
5 многоугольник, также известный как невыпуклый многоугольник, имеет по крайней мере один из внутренних углов, превышающий 180°.
Некоторые диагонали вогнутого многоугольника лежат вне замкнутой фигуры.Все вогнутые многоугольники неправильные, так как все внутренние углы имеют разную величину. Таким образом, вогнутые многоугольники никогда не бывают правильными.
Примеры : Дротик или наконечник стрелы в четырехугольниках, некоторых неправильных пятиугольниках и шестиугольниках
Вогнутый многоугольникСвойства
- Имеет по крайней мере один угол отражения больше 180° и меньше 360°; ∠DEF больше 180° и меньше 360°
- Имеет хотя бы одну вершину, направленную внутрь; вершина C направлена внутрь
- Имеет одну или несколько диагоналей, лежащих вне замкнутой фигуры; диагональ DF лежит вне замкнутой фигуры
- Если провести отрезок, пересекающий вогнутый многоугольник, он пересечет границу более двух раз
Сумма внутренних углов данного шестиугольника ABCDEF равна 720°. Если ∠ABC = 78°, ∠BCD = 140°, ∠CDE = 80°, ∠EFA =88°, ∠FAB = 130°.
Найдите ∠DEF и укажите, является ли многоугольник ABCDEF вогнутым.
Решение:
Как известно,
Сумма углов шестиугольника ABCDEF = 720°
Итак, ∠ABC + ∠BCD + ∠CDE +∠DEF + ∠EFA + ∠FAB =
78° + 140° + 80° +∠DEF + 88° + 130° = 720°
=> ∠DEF = 720° – 516°
=> ∠DEF = 204°
Поскольку ∠DEF больше 180°, многоугольник ABCDEF является вогнутым многоугольником. Также, если мы проведем линию, соединяющую точки D и F, мы обнаружим, что диагональ DF лежит вне замкнутой фигуры, что еще раз доказывает, что ABCDEF — вогнутый многоугольник.
Формулы
Площадь
Поскольку все стороны и внутренние углы вогнутого многоугольника не равны, стандартной формулы для определения их площади не существует. Чтобы определить площадь вогнутого многоугольника, мы должны разбить многоугольник на фигуры, такие как треугольник, прямоугольник, параллелограмм или другие фигуры, найти площадь каждой такой фигуры и, наконец, сложить их, чтобы получить общую площадь многоугольника.
Таким образом, площадь вогнутого многоугольника равна:
Площадь ( A ) = сумма площадей всех фигур, доступных в пределах многоугольника
Периметр
Это общее расстояние, пройденное вокруг границы многоугольника. Таким образом, периметр вогнутого многоугольника получается простым сложением длин всех сторон. Таким образом, периметр равен:
Периметр ( P ) = сумма всех сторон многоугольника
Давайте разберемся с этими понятиями на примерах.
Найдите площадь и периметр вогнутого многоугольника с заданными размерами сторон.
Решение:
Данный многоугольник разбит на три прямоугольника. Нахождение площади каждого прямоугольника и их сложение даст площадь многоугольника.
Таким образом, площадь многоугольника = Площадь прямоугольника ABCD + Площадь прямоугольника GDHF + Площадь прямоугольника EFIJ
= (14 x 4) + (6 x 4) + (14 x 4)
= 56 + 24 + 56
= 136 квадратных единиц
Периметр многоугольника = AB + BD + DF +FJ + IJ+ EI + EH + GH + CG + AC
= (14 + 4 + 6 + 4 +14 + 4 +10 + 6 +10+ 4)
= 76 единиц
Найдите все стороны данного вогнутого многоугольника.
Затем найдите его площадь и периметр. (Уловка: Разделите данный неправильный многоугольник на два правильных многоугольника)
Решение:
Данный многоугольник разделен на один прямоугольник и один квадрат. Нахождение площади прямоугольника и квадрата и их сложение даст площадь многоугольника.
Таким образом, площадь многоугольника = Площадь прямоугольника ABGF + Площадь квадрата CDEG
= (22 x 12) + (8x 8)
= 264 + 64
= 328 квадратных единиц
Периметр многоугольника = AB + BC + CD + DE + FE + AF
= (12 + 14 + 8 + 8 + 20 + 22)
= 84 ед. = общее количество сторон многоугольника
Внешние углы
Как и для всех других многоугольников, теорема о сумме внешних углов, утверждающая, что сумма всех внешних углов равна 360°, верна для всех вогнутых многоугольников.
Часто задаваемые вопросы
Q1. Сколько сторон у выпуклого многоугольника?
Ответ .