Формула цилиндра поверхности: Площадь поверхности цилиндра формула и калькулятор онлайн

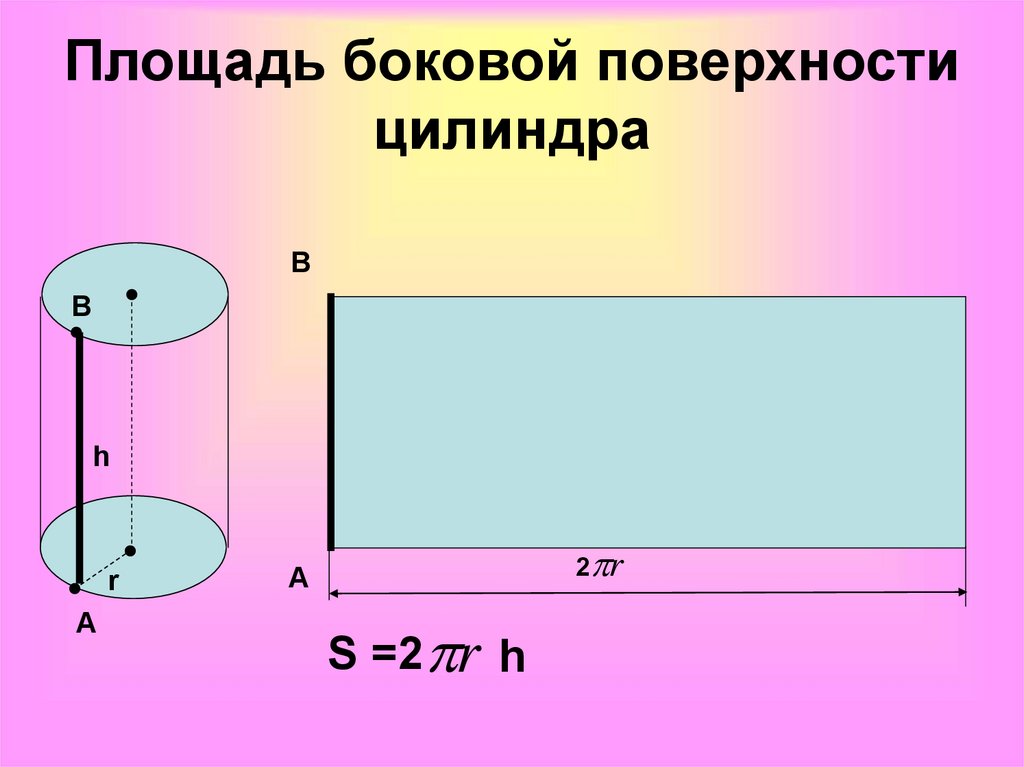
площадь боковой поверхности. Формула площади боковой поверхности цилиндра

При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.

Понятие цилиндра

Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.

• Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
• Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
• Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
• Под осью подразумевают прямую, проходящую через оба основания фигуры.
• Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.

Существуют разновидности данной объемной фигуры:

1. Под круговым подразумевают цилиндр, направляющая которого – это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
2. Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
3. Третий вид — скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
4. Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.

Условные обозначения

Традиционно основные «компоненты» цилиндра принято называть следующим образом:

• Радиус основания – R (он же заменяет аналогичную величину стереометрической фигуры).
• Образующая – L.
• Высота – H.
• Площадь основания – S_осн (иначе говоря, необходимо найти указанный параметр круга).
• Высоты скошенного цилиндра – h₁,h₂ (минимальная и максимальная).
• Площадь боковой поверхности – S_бок (если ее развернуть, то получится своего рода прямоугольник).
• Объем стереометрической фигуры – V.
• Площадь полной поверхности – S.

«Компоненты» стереометрической фигуры

Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.

Основными составляющими фигуры являются:

1. Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.
2. Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
3. Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина – параллельные хорды стереометрической фигуры.
4. Под осевым сечением подразумевают расположение плоскости через центр тела.
5. И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.

Основные формулы для работы с цилиндром

Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.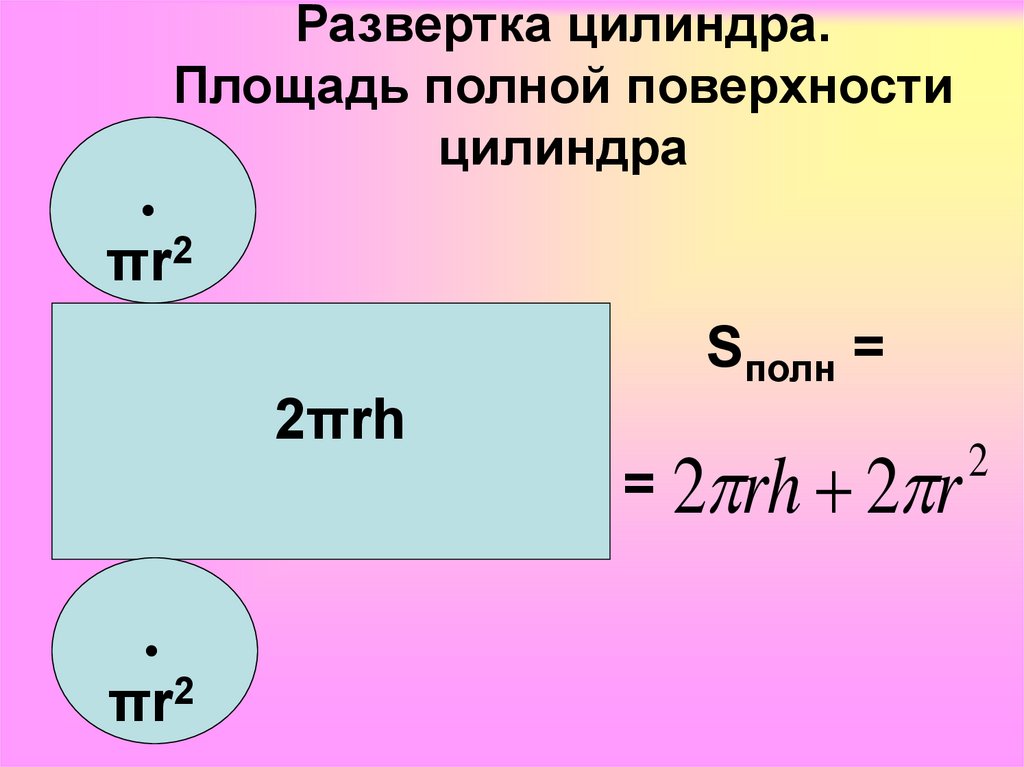

Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем – для прямого.

Примеры с разобранным решением

Задача 1.

Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается _<ACD = 30°

Решение. Поскольку известны величины диагонали и угла, то в таком случае:

• CD = AC*cos 30°.

Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.

Аналогично, можно найти и значение AD:

• AD = AC*sin 30°

Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра.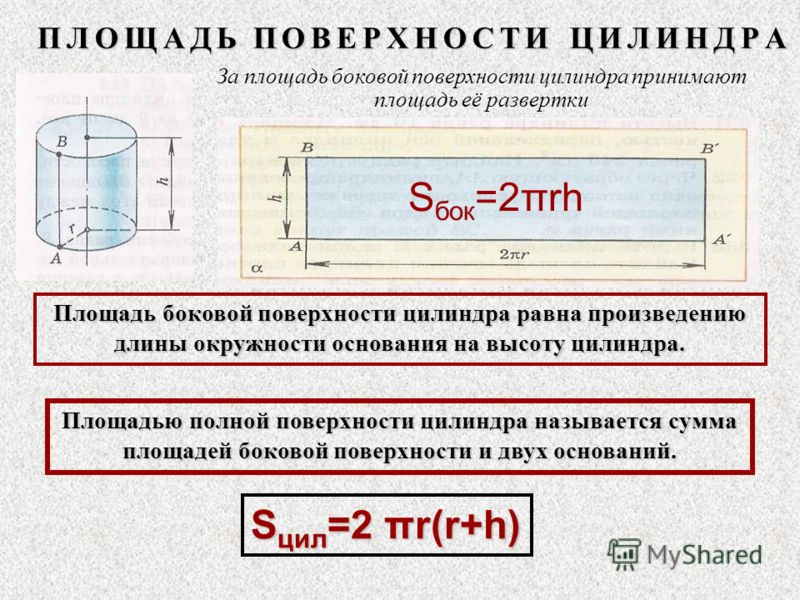 Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.

Задача 2.

Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?

Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.

Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.

Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.

Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.

Ответ: S_min будет достигнута при h = 1/32 см, R = 64 см.

Задача 3.

Дана стереометрическая фигура – цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.

Решение.

Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.

ВК² = ВМ² + МК²

МК² = ВК² – ВМ²

МК² = 17² – 15²

МК² = 64

МК = 8

Отсюда можно сделать вывод, что МК = ВС = 8 см.

Следующий шаг – проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.

AD – диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.

BC – прямая, расположенная на плоскости имеющегося прямоугольника.

ABCD – трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.

Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.

Для этого необходимо найти величины AD и ОС.

Ответ: сечение располагается 3 см от оси.

Задачи на закрепление материала

Пример 1.

Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра.

Пример 2.

Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.

Как найти площадь поверхности цилиндра? – Обзоры Вики

Формула для расчета общей площади поверхности цилиндра представляет собой общую площадь поверхности цилиндра. = 2u03c0r(ч + г), а формула площади криволинейной поверхности цилиндра: площадь криволинейной/боковой поверхности цилиндра = 2u03c0rh, где «r» — радиус основания, а «h» — высота цилиндра.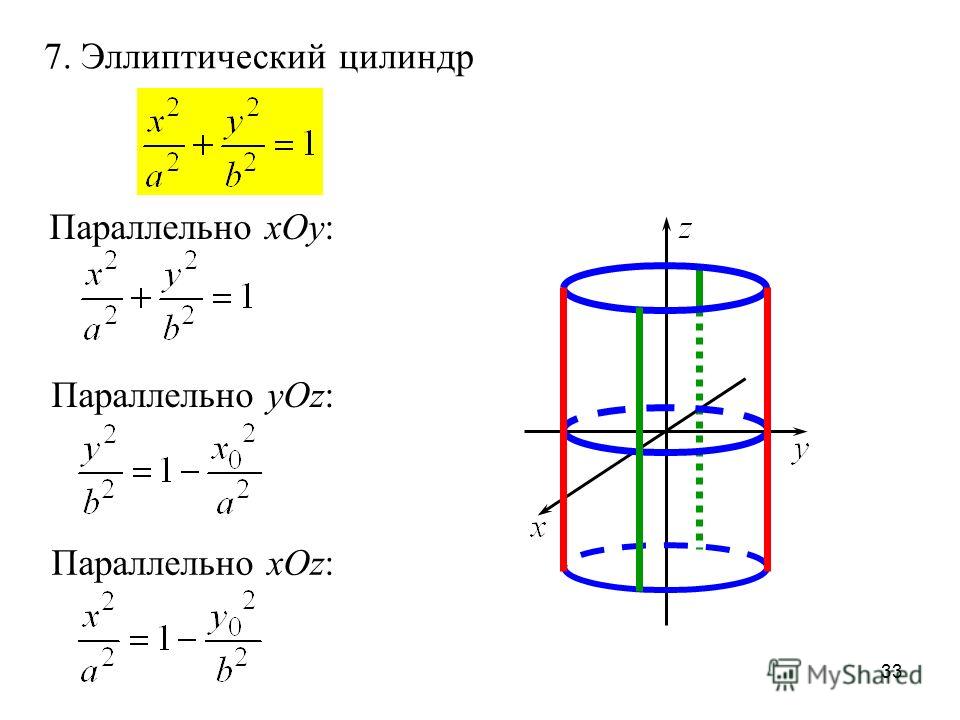

Аналогично, какова формула площади поверхности? переменные:

Формула площади поверхности	Значение площади поверхности
SA = 2B + Ph	Найдите площадь каждого лица. Сложите все области.
SA = B + 12sP	Найдите площадь каждого лица. Сложите все области.
СА=2B+2u03c0rh	Найдите площадь основания, умноженную на 2, затем добавьте площади к площадям прямоугольника, равным длине окружности, умноженной на высоту.

• 17 сентября 2020 г.

Как найти площадь поверхности цилиндрической призмы? Помните формулы для площади боковой поверхности призмы ph и полной площади поверхности рН+2В . Поскольку основанием цилиндра является окружность, мы подставляем 2πr вместо p и πr2 вместо B, где r — радиус основания цилиндра.

Какова общая площадь поверхности полого цилиндра? Общая площадь поверхности полого металлического цилиндра, открытого с обоих концов, с внешним радиусом 8 см и высотой 10 см составляет 338π см2.

Во-вторых, как найти площадь поверхности и объем цилиндра? То, что нужно запомнить

1. Площадь цилиндра = 2πr ² + 2πрч.
2. Объем цилиндра = πr ² h.
3. Вам нужно знать радиус и высоту, чтобы определить как объем, так и площадь цилиндра.
4. Ответы на проблемы с объемом всегда должны быть в кубических единицах.
5. Ответы на проблемы с площадью поверхности всегда должны быть в квадратных единицах.

Как найти боковую поверхность и площадь поверхности цилиндра?

Эту площадь боковой поверхности можно рассчитать следующим образом: умножение периметра основания на высоту призмы. Для прямого кругового цилиндра радиуса r и высоты h боковая площадь равна площади боковой поверхности цилиндра: A = 2πrh.

то какова площадь поверхности правого цилиндра внизу? Общая площадь поверхности закрытого цилиндра равна: A = L + T + B = 2πrh + 2(πr²) = 2πr (h + r)

Площадь поверхности цилиндра в квадрате или в кубе? Площадь круглой трубы — это длина вокруг трубы (окружность конца круга), умноженная на длину трубы. 2 конца{выровнять*}.

Как найти размеры цилиндра?

Сколько размеров в цилиндре?

Цилиндр — это трехмерный фигура похожа на призму, но с кругами в основании.

Каковы 3 измерения цилиндра? Цилиндр — это трехмерная фигура, имеющая две круглые грани, одну вверху и одну внизу. одна изогнутая поверхность. Цилиндр имеет высоту и радиус. Высота цилиндра — это перпендикулярное расстояние между верхней и нижней гранями.

Как найти площадь поверхности полого полуцилиндра?

Как найти площадь поверхности круга? Площадь круга пи умножить на квадрат радиуса (A = π r²).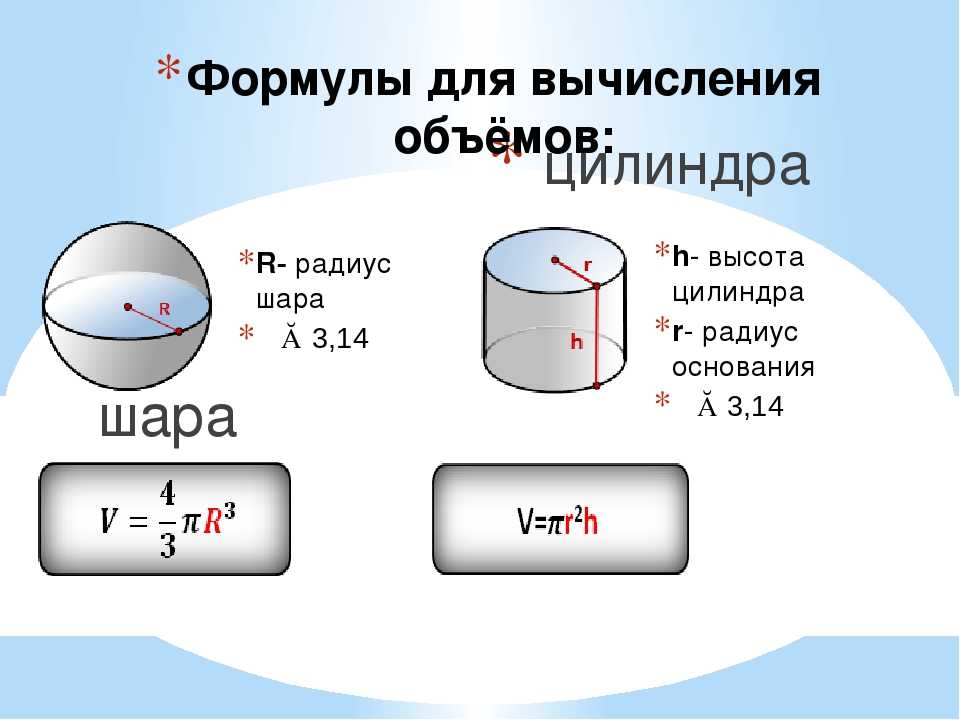 Узнайте, как использовать эту формулу, чтобы найти площадь круга при заданном диаметре.

Как вы используете размер в цилиндрическом?

Имеют ли цилиндры ширину? Разрезав и развернув этикетку банки с овощами, мы видим, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника равна окружности основания цилиндра, а ширина — высота цилиндра.

Как найти недостающую длину цилиндра?

Сначала разделите диаметр на 2 и подставьте значения объема, пи и радиуса в формулу объема цилиндра. Далее возведите радиус в квадрат и перемножьте значения между собой. Потом, разделить обе стороны на 200.96 для ответа, не забывая включить соответствующую единицу измерения.

Каков диаметр цилиндра? Диаметр или расстояние поперек цилиндра, которое проходит через центр цилиндра, равно 2R (в два раза больше радиуса).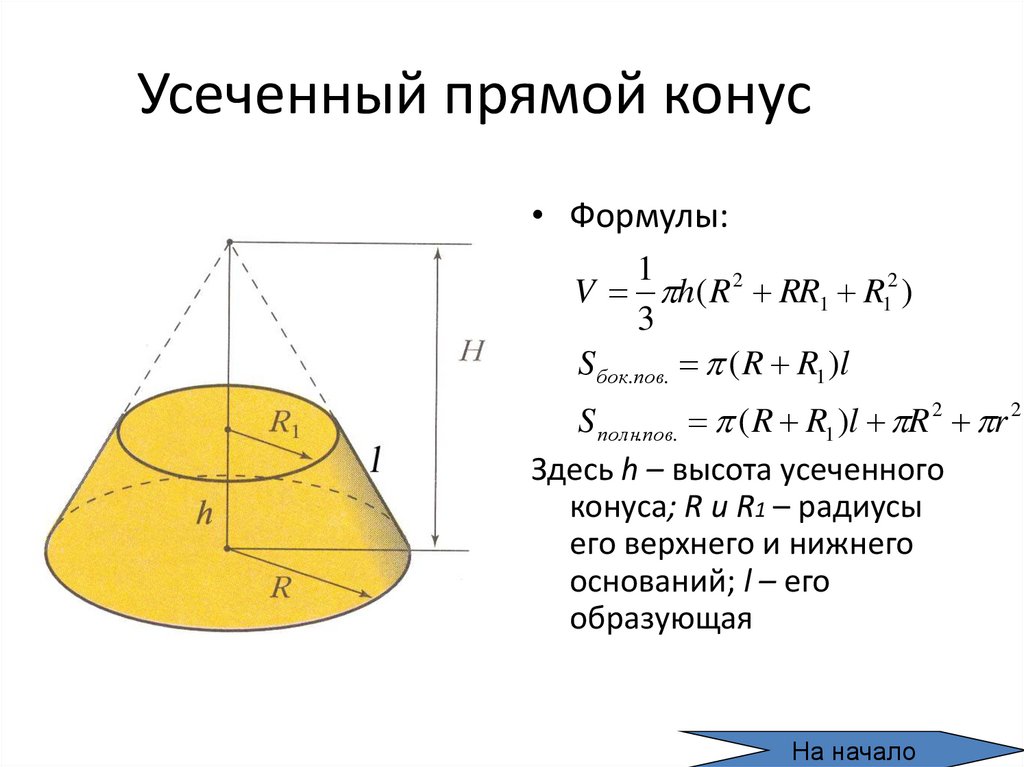

Какая ширина цилиндра?

Длина прямоугольника равна окружности основания цилиндра, а ширина равна высота цилиндра. Расстояние вокруг края банки — это окружность основания цилиндра, а также длина L прямоугольной этикетки. Высота цилиндра равна ширине W прямоугольной этикетки.

Что мы измеряем мерным цилиндром? Градуированный цилиндр, также известный как мерный цилиндр или смесительный цилиндр, является обычным лабораторным оборудованием, используемым для измерить объем жидкости. Имеет узкую цилиндрическую форму. Каждая отмеченная линия на градуированном цилиндре представляет собой измеренное количество жидкости.

Нахождение объема и площади поверхности цилиндра | Преалгебра |

Результаты обучения

• Найдите объем и площадь поверхности цилиндра

Если вы когда-нибудь видели банку газировки, то знаете, как выглядит цилиндр. Цилиндр — это объемная фигура с двумя параллельными окружностями одинакового размера вверху и внизу.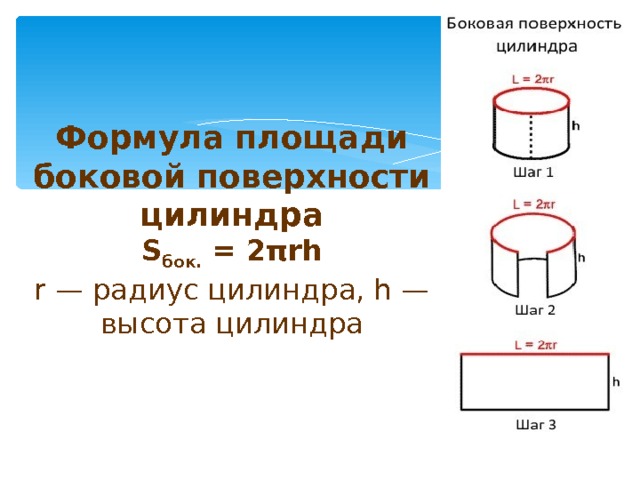 Верх и низ цилиндра называются основаниями. Высота

hhh

цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем работать здесь, стороны и высота,

hhh

, будут перпендикулярны основаниям. Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.

Прямоугольные тела и цилиндры в чем-то похожи, потому что они оба имеют два основания и высоту. Формула объема прямоугольного тела

V=BhV=BhV=Bh

также может быть использована для нахождения объема цилиндра.

Для прямоугольного тела площадь основания

ВВВ 9{2}πr2

. На изображении ниже показано, как формула

V=BhV=BhV=Bh

используется для прямоугольных тел и цилиндров.

Увидев, как цилиндр похож на прямоугольное твердое тело, вы сможете легче понять формулу объема цилиндра.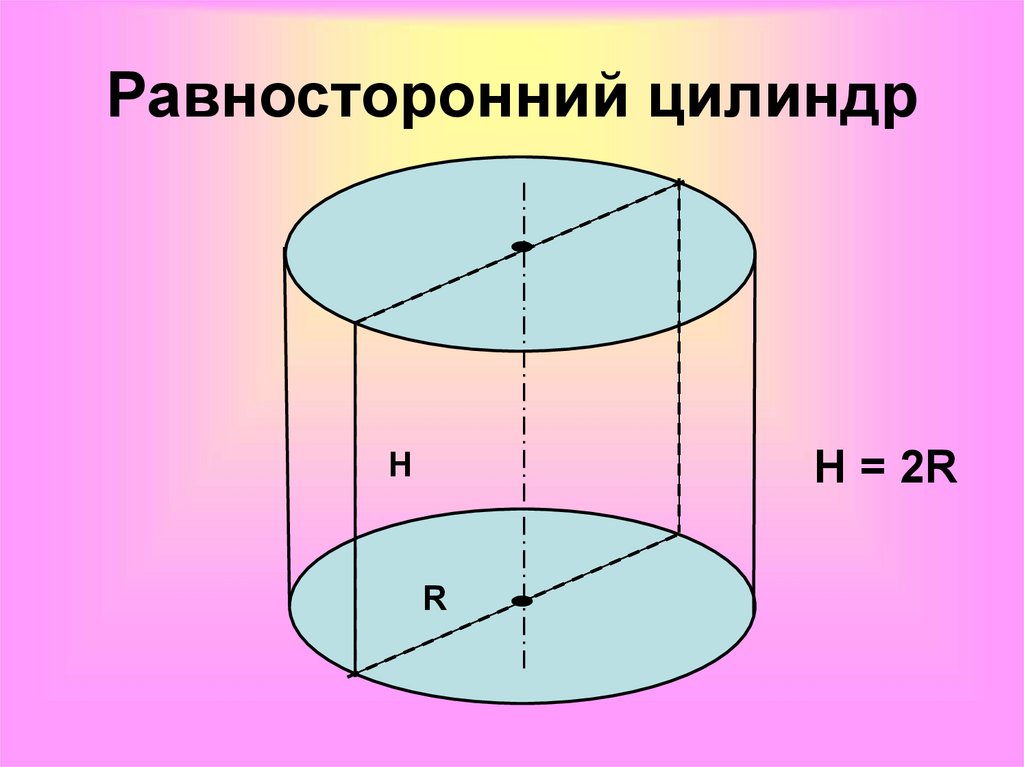

Чтобы понять формулу площади поверхности цилиндра, представьте себе банку с овощами. У него три поверхности: верхняя, нижняя и часть, образующая стенки банки. Если вы аккуратно отрежете этикетку сбоку от банки и развернете ее, то увидите, что это прямоугольник. См. изображение ниже.

Разрезав и развернув этикетку банки с овощами, мы видим, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — высота цилиндра.

Расстояние вокруг края банки — это окружность основания цилиндра, а также длина

LLL

прямоугольной этикетки. Высота цилиндра равна ширине

WWW

прямоугольной этикетки. Таким образом, площадь этикетки можно представить как 9{2}+2\pi rhS=2πr2+2πrh

Объем и площадь поверхности цилиндра

Для цилиндра с радиусом

rrr

и высотой

h:h:h:

пример

Цилиндр имеет высоту

555

сантиметров и радиус

333

сантиметров.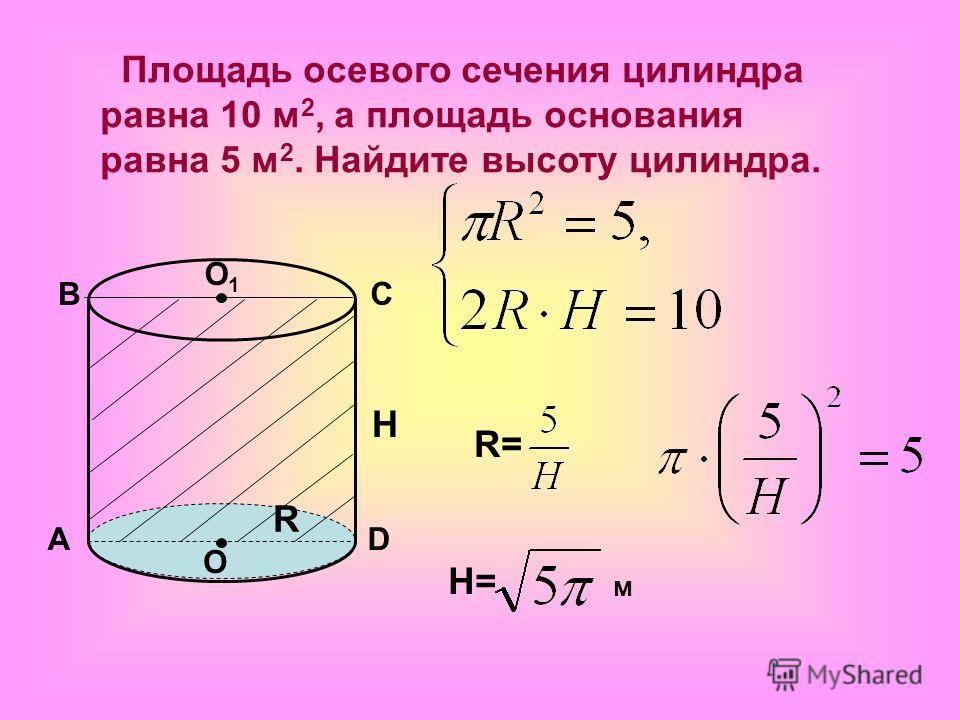 Найдите 1. объем и 2. площадь поверхности.

Решение

Шаг 1. Прочтите проблему. Нарисуй рисунок и подпиши цифру 9.0012 это с данной информацией.

1.
Шаг 2. Определите , что вы ищете.	объем цилиндра
Шаг 3. Имя. Выберите переменную для ее представления.	пусть В = объем
Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель. (Используйте 9{2}\cdot 5В≈(3,14)32⋅5
Шаг 5. Решить.	В≈141,3В\приблизительно 141,3В≈141,3
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты.
Шаг 7.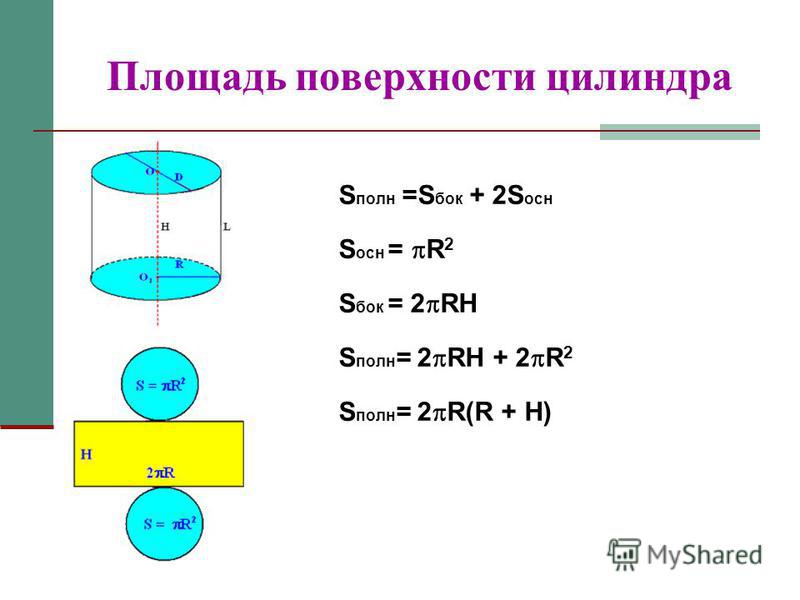 Ответьте на вопрос.	Объем примерно 141,3141,3141,3 кубических дюймов.

9{2}+2\влево(3,14\вправо)\влево(3\вправо)5S≈2(3,14)32+2(3,14)(3)5

2.
Шаг 5. Решить.	S≈150,72S\ок. 150,72S≈150,72
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты.
Шаг 7. Ответьте на вопрос.	Площадь поверхности составляет приблизительно 150,72150,72150,72 квадратных дюймов.

попробовать

пример

Найдите 1. объем и 2. площадь поверхности банки газировки. Радиус основания

444

сантиметров, а высота

131313

сантиметров.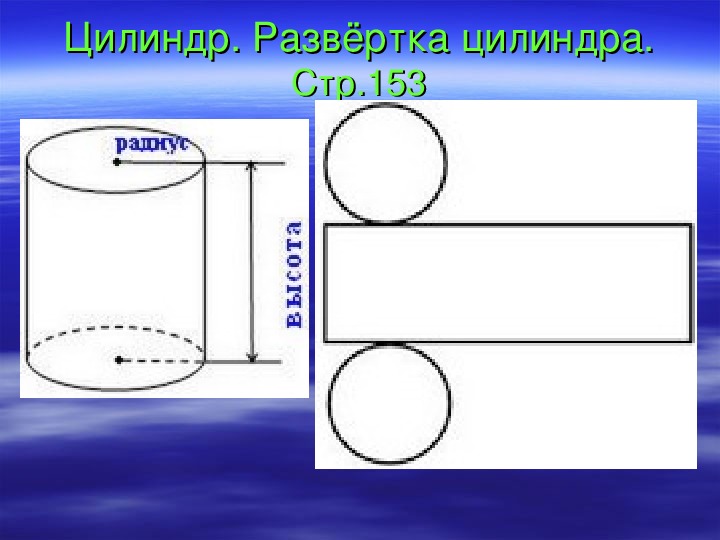 Предположим, что банка имеет форму цилиндра.

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и подпишите ее с помощью данной информации.

1.
Шаг 2. Определите , что вы ищете.	объем цилиндра
Шаг 3. Имя. Выберите переменную для ее представления.	пусть В = объем
Шаг 4. Перевести. Напишите соответствующую формулу. Заменитель. (Используйте 3.143.143.14 для π\pi π 9{2}\cdot 13В≈(3.14)42⋅13
Шаг 5. Решить.	В ≈ 653,12 В\приблизительно 653,12 В ≈ 653,12
Шаг 6. Проверка: Мы предоставляем вам проверить.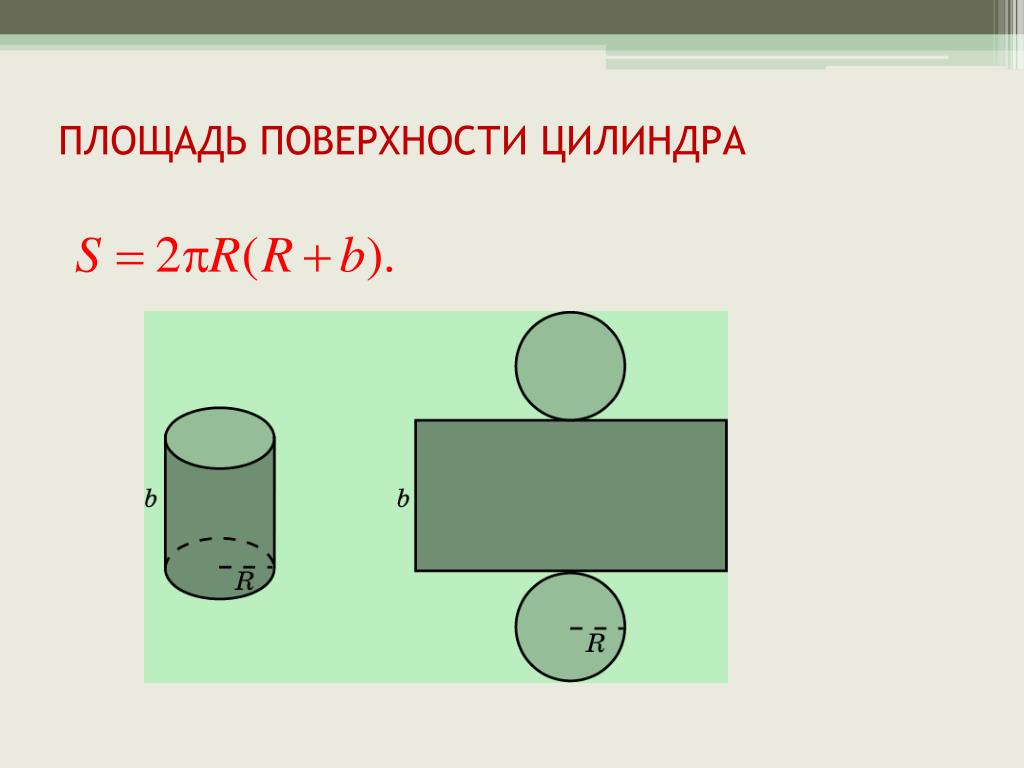
Шаг 7. Ответьте на вопрос.	Объем примерно 653,12653,12653,12 кубических сантиметров.

2.
Шаг 2. 9{2}+2\влево(3,14\вправо)\влево(4\вправо)13S≈2(3,14)42+2(3,14)(4)13
Шаг 5. Решить.	S≈427,04S\ок. 427,04S≈427,04
Шаг 6. Проверка: Мы оставляем вам возможность проверить свои расчеты.
Шаг 7. Ответьте на вопрос.	Площадь поверхности составляет приблизительно 427,04427,04427,04 квадратных сантиметров.

попробуй

Лицензии и авторство

Контент по лицензии CC, конкретное авторство

• Преалгебра. Предоставлено : OpenStax. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно с http://cnx.org/contents/[email protected]

Площадь изогнутой поверхности цилиндра0009

Если плоскость разрезает твердое тело параллельно его основанию, то открытая поверхность называется сечением . Твердое тело, такое как банка из-под напитка, является цилиндром , если его поперечное сечение круг. Радиус круглого сечения называется радиусом цилиндр и прямая, проходящая через центр каждого круглое сечение называется ось цилиндра. Длина оси называется высотой цилиндра. Радиус и высота цилиндра представлены как r и h соответственно. Рассмотрим цилиндрическую банку радиусом х и высотой х . Чтобы определить формулу для криволинейной поверхности цилиндрической банку, плотно оберните банку листом бумаги и закрепите ее скотчем. вместе. Обрежьте бумагу сверху и снизу, чтобы она соответствовала форме банка. Затем сдвиньте бумагу с банки и разрежьте эту бумагу. цилиндра, параллельного его оси, так, чтобы он образовывал прямоугольник, показанный на следующую схему.
Просто резюмируя приведенное выше обсуждение: Площадь криволинейной поверхности ( CSA ) цилиндра с радиусом r и высота ч равна Пример 23 Найдите площадь криволинейной поверхности цилиндрической жести радиусом 7 см и высотой 4 см. Решение:
Примечание: Круглое основание цилиндра нарисовано в виде эллипса. Основные термины плоскость, поперечное сечение, цилиндр, радиус цилиндра, ось цилиндра, высота цилиндр, изогнутая поверхность ( CSA )

---

| Домашняя страница | Заказать программное обеспечение по математике | О сериале | Учебники по математическому программному обеспечению |
| Программное обеспечение по математике для 7 класса | Программное обеспечение по математике для 8 класса | 9 годПрограммное обеспечение по математике | Программное обеспечение по математике для 10 класса |
| Программное обеспечение для домашних заданий | Программное обеспечение для репетиторов | Математическая программная платформа | Пробное математическое программное обеспечение |
| Обратная связь | О mathsteacher.