Формула длины медианы треугольника: Все формулы медианы треугольника

Длина медианы правильного треугольника – формула, примеры

3.9

Средняя оценка: 3.9

Всего получено оценок: 131.

3.9

Средняя оценка: 3.9

Всего получено оценок: 131.

Медиана – это один из характеризующих отрезков треугольника, наравне с биссектрисой и высотой. Особую сложность у учеников часто вызывают задачи на нахождение медианы. В обычном случае приходится применять формулу, но для правильного треугольника можно вывести упрощенную версию нахождения медианы.

Необходимые данные

Для вывода формул потребуется вспомнить несколько теоретических выкладок:

• Медиана это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке.
• В равнобедренном треугольнике, медиана, проведенная к основанию, является биссектрисой и высотой. А правильный треугольник это частный случай равнобедренного треугольника, у которого основанием может выступать любая из сторон. 2}\over{4}}=a*{{3}\over{\sqrt{2}}}$$

  Получилась та же формула длины медианы правильного треугольника. Значит, вывод первым способом был осуществлен верно и можно использовать любой из двух способов, если вы вдруг забыли формулу нахождения медианы правильного треугольника.

  Рис. 3. Точка пересечения медиан правильного треугольника.

  Последний метод очень часто используется не только для вывода формул правильного треугольника, но и для решения задач.

  Что мы узнали?

  Мы несколькими методами вывели формулу длины медианы правильного треугольника. Указали на метод решения простых задач на нахождение характеристик правильного треугольника, а так же вспомнили основные свойства медианы.

  Тест по теме

  Доска почёта

  Чтобы попасть сюда — пройдите тест.

  • Милана Швецова

    3/5

  • Оксана Шмидт

    3/5

  Оценка статьи

  3.9

  Средняя оценка: 3.

  9

  Всего получено оценок: 131.

  ---

  А какая ваша оценка?

  Калькулятор расчета длины медианы треугольника

  ---

  Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

  Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.

  Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника

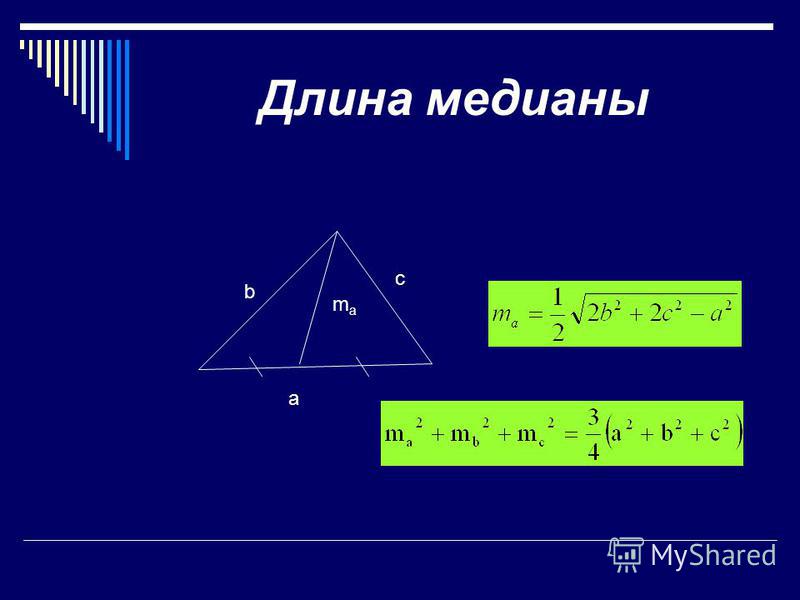
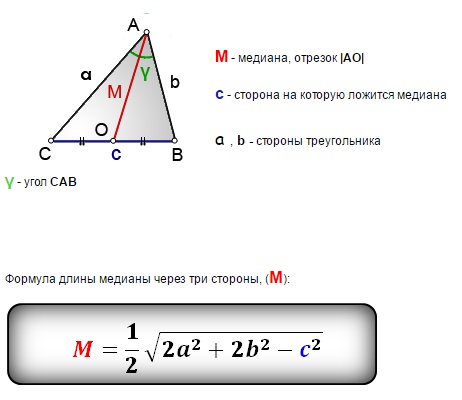
  Формула расчета длины медианы

   

   

   

  где,

  • a,b,c — Длина сторон треугольника.

  Пример расчета медиан:

  Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.

  Получаем:

  A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )

  Решение:

  Шаг 1:

  Найдем длину сторон a,b,c используя формулу

  d = √((x₂ — x₁)² + (y₂ — y₁)²⁾

  Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )

  a = √((5 — 8)² + (6 — 9)² )= 4.242

  Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )

  b = √((1 — 5)² + (5 — 6)²⁾ = 4.123

  Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )

  c = √((8 — 1)² + (9 — 5)²⁾ = 8.062

  Шаг 2:

  Полученные значения a,b,c применяем в формулы

  m_a = (1/2) √2c² + 2b² — a²

  m_b = (1/2) √(2c² + 2a² — b² )

  m_c = (1/2) √(2a² + 2b² — c² )

  • m_a = (1/2)√(2(8. 062)² + 2(4.123)² — 4.242² )= 6.042
  • m_b = (1/2)√(2(8.062)² + 2(4.242)² — 4.123² )= 6.103
  • m_c = (1/2)√2(4.242)² + 2(4.123)² — 8.062² = 1.118

  Свойства Медиан Треугольника

  • Медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
  • Треугольник делится тремя медианами на шесть равновеликих треугольников.
  • Большей стороне треугольника соответствует меньшая медиана.
  • В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равняется половине гипотенузы.
  • Из отрезков, образующих медианы, можно составить треугольник, то есть их длины удовлетворяют неравенству треугольника.

  людей нашли эту статью полезной. А Вы?

  Урок Длина медианы треугольника

  Этот Урок (Длина медианы треугольника) создан пользователем ikleyn(48318)   : Просмотр исходного кода, Показать
  О ikleyn : 9001 0 Этот урок посвящен формуле, выражающей длину медианы треугольника.
  Представлено доказательство формулы, основанной на Законе косинусов (см. урок Доказательство закона косинусов, пересмотренный в теме Тригонометрия из
  раздел Алгебра-II на этом сайте). Также приведены примеры, показывающие, как использовать эту формулу.

  Теорема 1
  В треугольнике со сторонами a , b и c медиана, проведенная к стороне c , имеет длину

  = . Доказывать.
  

  Доказательство На рисунке 1 показан треугольник ABC со сторонами a (BC) , b (AC) и c (AB) и                              медиана м ( CD 90 004 ) обращено в сторону c . Пусть d будет длиной отрезка AD и e будет длиной отрезка DB медиана CD делит сторону AB . Обозначим как и углы при пересечении медианы CD и стороны АБ . Применить Закон косинусов , чтобы выразить длину стороны AC треугольника ADC = . Применить Закон косинусов , чтобы выразить длину стороны BC треугольника BDC = .

  Рисунок 1 . К теореме 1

  Теперь возьмем сумму двух последних равенств. Обратите внимание, что , поскольку углы и являются дополнительными углами. Также обратите внимание, что, поскольку CD — это
  медиана. Следовательно, при взятии суммы условия и взаимно компенсируют друг друга. Итак, после суммирования получаем
  + = + + .

  Замените здесь, используя тот факт, что CD является медианой. Получаем
  + = + + ,
  или
  = ( + — )/4.
  Вот что нужно продемонстрировать. Доказательство завершено.

  Теорема 2
  В треугольнике со сторонами

  a , b и c длины медиан , и , проведенные к сторонам a , b и c соответственно удовлетворяют тождеству
  = . Доказывать.

  Доказательство
  На основании Теоремы 1 имеем три равенства

  = ,

  = , и

  = .

  Суммируя эти равенства, получаем тождество

  = .

  Это именно то, что нужно продемонстрировать. Теорема 2 доказана.

  Пример 1 В треугольнике длины сторон равны a = 5 , b = 6 и c = 4 ( рис. 2 ). Найдите длину медианы, проведенной к стороне c . Раствор Применить формулу средней длины = = = =              = . Ответить . = =~ 5,148 (приблизительно).

  Рисунок 2 . К Пример 1

  
  

  Пример 2 В равнобедренном треугольнике боковая сторона имеет длину 4 . Медиана, проведенная к боковой стороне, имеет длину 3 ( Рисунок 3 ). Найдите длину основания треугольника. Раствор Пусть будет длина основания треугольника. Применить формулу средней длины. Вы получаете уравнение . Упростите это уравнение шаг за шагом, как показано ниже: , , , , , . Ответить . Основание треугольника имеет длину .

  Рисунок 3 . К Пример 2

  Для навигации по урокам по свойствам треугольников используйте этот файл/ссылку  Свойства треугольников.

  Для навигации по всем темам/урокам онлайн-учебника по геометрии используйте этот файл/ссылку  ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.

  Медиана треугольника | Что такое медиана треугольника

  Содержание

  Этот пост также доступен в: हिन्दी (хинди)

  Треугольник — одна из самых важных двумерных фигур в геометрии. Треугольники обладают определенными свойствами, которые используются для решения задач. Одним из таких свойств является медиана треугольника.

  Давайте разберемся, что такое медиана треугольника и ее свойства.

  Что такое медиана треугольника?

  Отрезок, соединяющий вершину с серединой стороны, противоположной этой вершине, называется медианой треугольника. Треугольник может иметь три медианы, соединяющие каждую из вершин с серединой противоположной стороны.

  На приведенном выше рисунке в $\triangle \text{ABC}$ точка $\text{D}$ является серединой стороны $\text{BC}$. $\text{AD}$ — это отрезок, соединяющий вершину $\text{A}$ с $\text{D}$ и, таким образом, являющийся одной из медиан $\треугольника \text{ABC}$.

  СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

  Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.

  Свойства медианы треугольника

  Ниже приведены свойства медианы треугольника, которые помогут вам ее идентифицировать.

  • Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противоположной стороны.
  • Он делит противоположную сторону пополам, разделяя ее на две равные части.
  • Медиана треугольника далее делит треугольник на два треугольника, имеющих одинаковую площадь.
  • Независимо от формы или размера треугольника, три его медианы сходятся в одной точке.
  • Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан образует центр тяжести треугольника.
  • Каждая медиана треугольника делит его на два меньших треугольника с равными площадями. Три медианы делят треугольник на шесть меньших треугольников равной площади. 92}{4}$.

    Как найти медиану треугольника с заданными координатами?

    Если известны координаты трех вершин треугольника, для определения длины медианы треугольника используются следующие шаги.

    Шаг 1: Используя координаты вершин треугольника, найдите координаты середины отрезка, на котором образована медиана. Это можно сделать с помощью формулы средней точки. Формула для средней точки: $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$, где $\left(x_1, y_1 \right)$ и $ \left(x_2, y_2 \right)$ — координаты концов отрезка. 92}$ где $\left(x_1, y_1 \right)$ и $\left(x_2, y_2 \right)$ — координаты медианы.

    Разница между медианой и высотой треугольника

    Ниже приведены различия между медианой и высотой треугольника.

    Медиана треугольника	Высота треугольника .	Высота треугольника — это расстояние по перпендикуляру от основания до противоположной вершины.
    Всегда лежит внутри треугольника.	Может быть как снаружи, так и внутри треугольника в зависимости от типа треугольника.
    Делит треугольник на две равные части.	Не делит треугольник на две равные части.
    Делит основание треугольника пополам на две равные части.	Не делит основание треугольника пополам.
    Точка, где сходятся три медианы треугольника, называется центром тяжести треугольника.	Точка, где встречаются три высоты треугольника, называется ортоцентром этого треугольника.

    Ключевые выводы

    • Каждая медиана делит треугольник на два меньших треугольника с одинаковой площадью.
    • Центроид (точка, где они встречаются) является центром тяжести треугольника.
    • Периметр треугольника больше суммы трех его медиан.
    • Если два треугольника конгруэнтны, медианы конгруэнтных треугольников равны, так как соответствующие части конгруэнтных треугольников конгруэнтны.
    Типы систем координат

    Практические задачи

    1. Что такое медиана треугольника?
    2. Сколько медиан может быть у треугольника?
    3. Точка пересечения всех медиан треугольника называется _________.
    4. Найдите длину медианы AD, если координаты треугольника ABC заданы как A (4, 10), B (8, 2), C (-8, 4).

    Часто задаваемые вопросы

    Что такое медиана треугольника?

    Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, таким образом делящий эту сторону пополам. Все треугольники имеют ровно три медианы, по одной из каждой вершины.

    Как найти медиану треугольника с известными длинами сторон?

    Длину медианы треугольника можно вычислить, если известны длины трех сторон. 2}}{4}$, где медиана треугольника равна $m_a. $ стороны треугольника равны $a$, $b$, $c$, а медиана проходит по стороне $a$.

    Какими свойствами обладает медиана треугольника?

    Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противоположной стороны. Медиана треугольника делит противоположную сторону пополам, делит ее на две равные части. Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан называется центром треугольника.

    Заключение

    Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противоположной стороны. Медиана треугольника делит противоположную сторону пополам, делит ее на две равные части. Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан называется центром треугольника.

    Рекомендуемое чтение

    • Типы треугольников – определение и примеры
    • Что такое треугольник в геометрии — определение, формы и примеры
    • Пара углов – определение, схемы, типы и примеры
    • Построение углов (с помощью транспортира и компаса)
    • Типы углов в математике (острые, прямые, тупые, прямые и обратные)
    • Что такое угол в геометрии – определение, свойства и измерение
    • Как построить касательную к окружности (с шагами и иллюстрациями)
    • Тангенс окружности – значение, свойства, примеры
    • Углы в круге – значение, свойства и примеры
    • Хорда окружности – определение, свойства и примеры
    • Как нарисовать круг (с шагами и картинками)
    • Что такое круг — части, свойства и примеры
    • Как построить перпендикулярную линию (с шагами и примерами)
    • Как построить параллельные линии (с шагами и примерами)
    • Как построить сегмент линии (с шагами и примерами)
    • Что такое коллинеарные точки в геометрии – определение, свойства и примеры
    • Что такое поперечная линия в геометрии – определение, свойства и примеры
    • Что такое параллельные линии в геометрии — определение, свойства и примеры
    • Что такое параллельные линии в геометрии — определение, условия и примеры
    • Что такое полупрямая в геометрии – определение, свойства и примеры
    • Что такое перпендикулярная линия в геометрии – определение, свойства и примеры
    • Разница между аксиомой, постулатом и теоремой
    • Линии в геометрии (определение, типы и примеры)
    • Что такое 2D-фигуры — имена, определения и свойства
    • 3D-фигуры — определение, свойства и типы

    Вам также может понравиться

    Законы экспонент – законы, доказательства и примеры

    Содержание Каковы законы экспоненты?1.

    No related posts.