Система координат на плоскости. Функции. Окружность
6.
Система координат на плоскости. Функции. Окружность
6.1.
Система координат на плоскости
Графиком линейной функции является прямая y = kx + b, пересекающая ось 0y в точке, ордината которой равна b. Коэффициент k называется угловым коэффициентом прямой (рис. 6.1).
Две прямые y1 = k1 x + b1 и y2 = k2 x + b2 являются параллельными, если их угловые коэффициенты k1 и k2 равны и b 1 ≠ b 2. Например, прямые y = 6x — 5 и y = 6x — 7 параллельны.
Две прямые y1
= k1
x + b1
и y2
= k2
x + b2
являются пересекающимися, если их угловые коэффициенты k1
≠ k2
. Например, прямые y = 4x — 3 и y = 5x — 4 пересекаются. Две пересекающиеся прямые имеют одну общую точку, координаты которой удовлетворяют каждому из уравнений прямых.
Точка лежит на прямой, если ее координаты удовлетворяют уравнению этой прямой. Например, точка N (2; 7) лежит на прямой y = 5x — 3, так как координаты точки удовлетворяют уравнению прямой: 7 = 5 ∙ 2 – 3.
Если точка лежит на оси абсцисс (0x), то ее ордината равна нулю (y = 0).
Если точка лежит на оси ординат (0у), то ее абсцисса равна нулю (x = 0).
График квадратичной функции называется параболой (рис. 6.2). Уравнение y = ax2 + bx + c, где a, b, с — действительные числа и a ≠ 0, является уравнением параболы, пересекающей ось 0y в точке, ордината которой равна c. Коэффициент a называется старшим коэффициентом. Если a > 0, то ветви параболы направлены вниз.
Координаты вершины параболы (xв ; yв ) находят с помощью формул:
Координаты точек пересечения параболы с осями находят с помощью следующих рассуждений.
Абсцисса точки пересечения параболы с осью 0y равна нулю, а ордината точки пересечения равна c, т.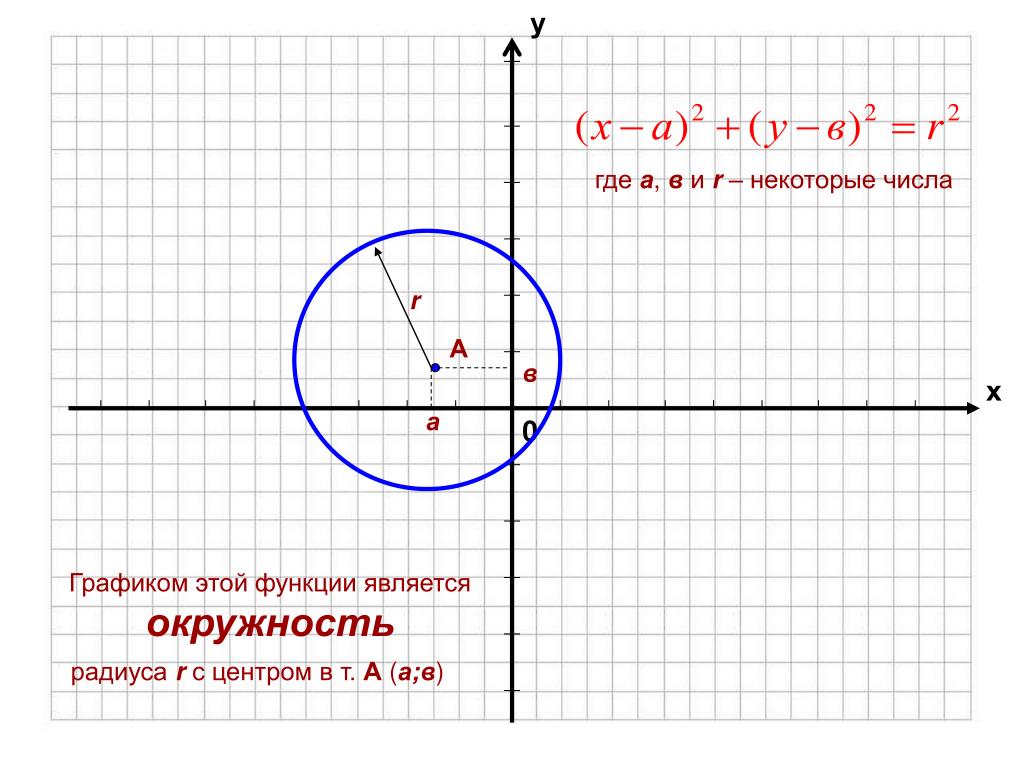
Ордината точки пересечения параболы с осью 0x равна нулю, а абсциссу точки пересечения можно найти, решив уравнение 0 = y = ax2 + bx + c.
На рисунке парабола пересекает ось 0y в точке C (0; 1), а ось 0x в точках A (-1; 0) и B (3; 0).
Парабола может иметь одну точку пересечения с осью 0x, может иметь две точки, и может не иметь точек пересечения. Определить количество точек пересечения параболы y = ax2 + bx + c с осью 0х можно с помощью результата дискриминанта квадратного уравнения ax2 + bx + c = 0:
1) если D > 0, то точек пересечения две;
2) если D < 0, то одна точка пересечения;
3) если D = 0, то точек пересечения нет.
Гипербола — — график обратной пропорциональности. Число k — коэффициент, k ≠ 0. В зависимости от знака коэффициента k гипербола будет располагаться либо в I и III квадранте, либо во II и IV (рис.
6.2.
Функции
D(y) — область определения функции, y — множество, на котором задается функция. При графическом способе задания функции ее область определения может считываться по графику. Для нахождения области определения надо спроектировать все точки графика функции на ось 0x. Если функция задана формулой, и ее область определения не указана, то это означает, что функция задается на естественной области определения.
E(y) — множество значений функции y, которые она принимает при всех значениях аргумента из ее области определения. Проще всего находить множество значений, если задан ее график. Необходимо спроектировать все точки графика функции на оси 0y. Получившееся множество точек является множеством значений функции.
Нули функции для функции f(x), заданной графически, — это абсциссы точек, в которых график функции пересекает ось абсцисс или касается ее. Чтобы найти нули функции, заданной графически, нужно решить уравнение f(x) = 0.
Функция f(x) убывает на множестве Х, если для любых x1
и x2
из множества Х, таких, что x1
> x2
, выполняется неравенство f(x1
) > f (x2
). Функция называется убывающей на множестве Х, если для любых двух значений аргумента из этого множества большему значению аргумента соответствует меньшее значение функции.
Функция называется убывающей на множестве Х, если для любых двух значений аргумента из этого множества большему значению аргумента соответствует меньшее значение функции.
Функция f(x) возрастает на множестве Х, если для любых x1
и x2
из множества Х, таких, что x1
< x2
, выполняется неравенство f(x
Функция y = f(x)называется четной, если для любого x из области определения функции выполняется равенство f(-x) = f(x). Свойство графика четной функции — симметричность относительно оси ординат.
Функция y = f(x)называется нечетной, если для любого x из области определения функции выполняется равенство f(-x) = -f(x). Свойство графика нечетной функции — симметричность относительно начала координат.
Свойства линейной функции
-
Область определения: .
-
Область значений:
-
, если k ≠ 0;
-
, если k = 0.
-
-
Монотонность:
-
если k > 0, то функция y возрастает на всей области определения;
-
если k < 0, то функция y убывает на всей области определения (рис. 6.4).
-
Свойства гиперболы
.
-
Область определения: .
-
Область значений: .
-
Монотонность:
-
если k > 0, то функция y убывает на промежутке и на промежутке ;
-
если k < 0, то функция y возрастает на промежутке .
 и на промежутке (рис. 6.5).
и на промежутке (рис. 6.5).
-
-
Функция является нечетной.
Свойства квадратичной функции
.
-
Область определения: .
-
График квадратного трехчлена — парабола с вершиной в точке с абсциссой:
-
направленная ветвями вверх, если a > 0;
-
направленная ветвями вниз, если a < 0.
-
-
Множество значений:
Свойства функции
-
Область определения.
-
Множество значений.
-
Монотонность: функция y возрастает на всей области определения (рис. 6.7).
6.3.
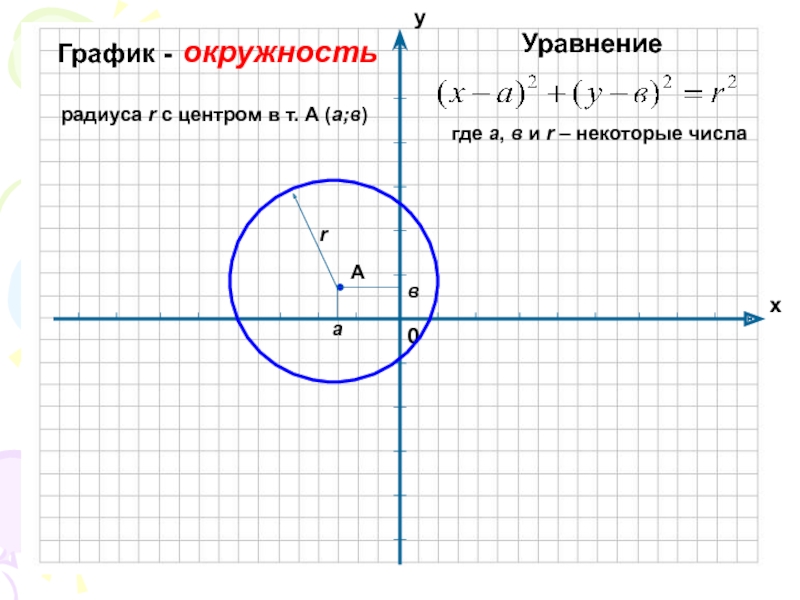
Уравнение окружности
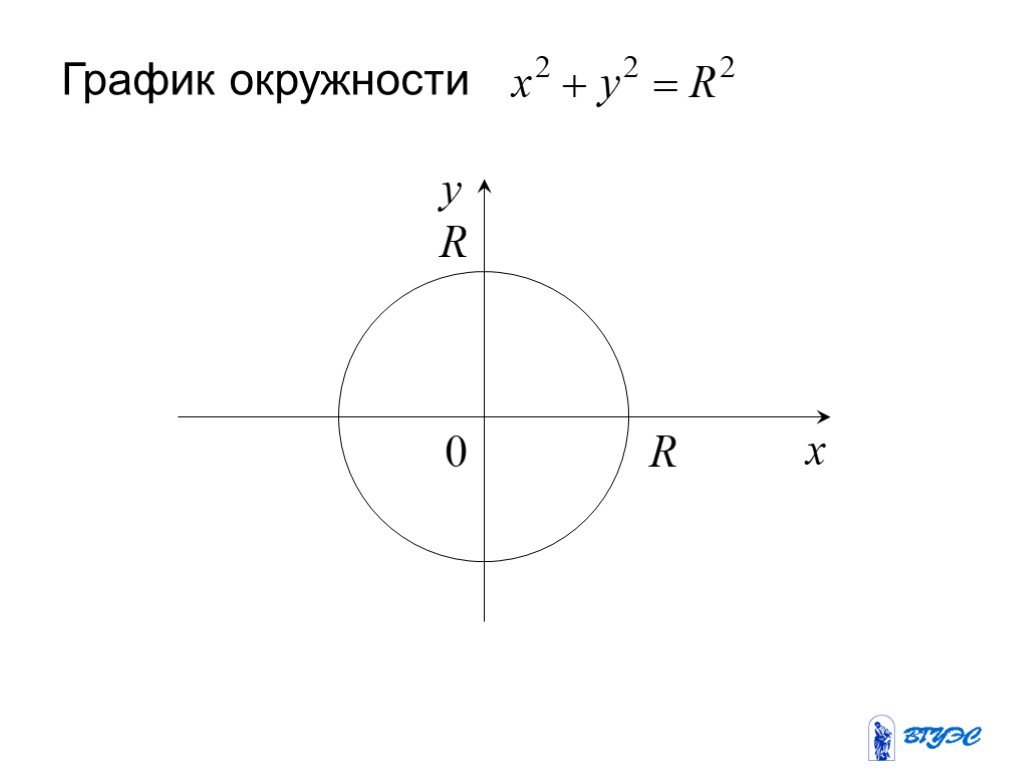
Уравнение окружности с центром в начале координат О (0; 0) и радиусом R имеет вид:
x2
+ y2
= R2
.
Уравнение окружности с центром в точке A (a; b) и радиусом R имеет вид:
Пример 6.1
График показывает движение парусной яхты, которая первую часть пути прошла под парусом. Спустив парус, она продолжила движение.
-
Найдите скорость яхты под парусом и без паруса (выразив ее в км/ч).
-
На каком расстоянии от начала движения находилась яхта через 50 мин., через 2 часа?
-
Сколько времени потребуется яхте на обратный путь, если она будет двигаться с той же скоростью, что и на первом участке под парусом?
Решение
-
Под парусом яхта прошла 30 км за 60 мин., значит, ее скорость была . Без паруса яхта прошла 5 км за 60 мин., следовательно, ее скорость равна 5 км/ч.
Ответ: скорость яхты под парусом 30 км/ч, скорость яхты без паруса 5 км/ч.
-
На графике найдем точку с абсциссой, равной 50.
 Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км.
Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км.Ответ: за 50 мин. яхта пройдет 25 км, за 120 минут — 35 км.
-
Обратный путь составляет 35 км. Скорость яхты — 30 км/ч.
Найдем время обратного пути: , что составляет 1 час 10 мин.
Ответ: 1 ч 10 мин.
Примеры заданий с комментариями
Задание 1
Прямая x + y = c, где c — некоторое число, касается гиперболы в точке с положительными координатами. Найдите c.
Решение
Если графики функций касаются, то они имеют одну общую точку. Тогда:
Так как общая точка только одна, то дискриминант последнего квадратного уравнения D = 0.
.
При с = 2 уравнение x2
– 2x + 1 = 0 имеет единственный корень x = 1. Это означает, что абсцисса точки касания графиков положительна. При этом ордината точки касания также положительна. Следовательно, с = 2 удовлетворяет условию задачи.
Следовательно, с = 2 удовлетворяет условию задачи.
Задание 2
Окружность, изображенная на рисунке, задана уравнением x2 + y2 = 16. Используя рисунок, определите, имеет ли система решение.
Решение
Система будет иметь решение в том случае, если прямая, построенная по второму уравнению системы, будет либо касаться окружности (в данном случае решение одно — точка касания), либо пересекать окружность в двух точках (решения два — точки пересечения). Чтобы проверить, имеет ли данная система решение, подставим во второе уравнение системы y = 1, получим, что x = 5 и x = 1, тогда y = 5. Получили две точки с координатами (5; 1) и (1; 5). Если данные точки нанести на представленной системе координат и соединить, то получим прямую, которая не касается и не пересекает нашу окружность. Таким образом, данная система решений не имеет.
Задание 3
На рисунке изображен график функции y = -x2
– 4x. Используя рисунок, решите неравенство -x2
≥ 4 x.
Решение
Чтобы решить неравенство, его необходимо преобразовать к виду заданной функции. Для этого 4 x перенесем влево. Получим:
-x2 – 4x ≥ 0.
По графику видно, что функция принимает значения большие или равные нулю выше оси абсцисс, т.е. на интервале [-4; 0]. Скобки квадратные, так как неравенство имеет не строгий знак.
Задание 4
Функция задана формулами:
1) ;
2) ;
3) ;
4) .
Найдите в этом перечне функции, графики которых проходят через начало координат.
Решение
Четвертая функция не подходит, так как это гипербола. Функция, проходящая через начало координат, имеет значения x = 0, y = 0. Таким образом, проверим все заданные функции на данное условие, подставив вместо x нуль. Получим, что первая и третья функции имеют значение y = 0. То есть первая и третья функции проходят через начало координат.
Задание 5
Запишите уравнение прямой, проходящей через точки A (-10; -7) и B (15; -2).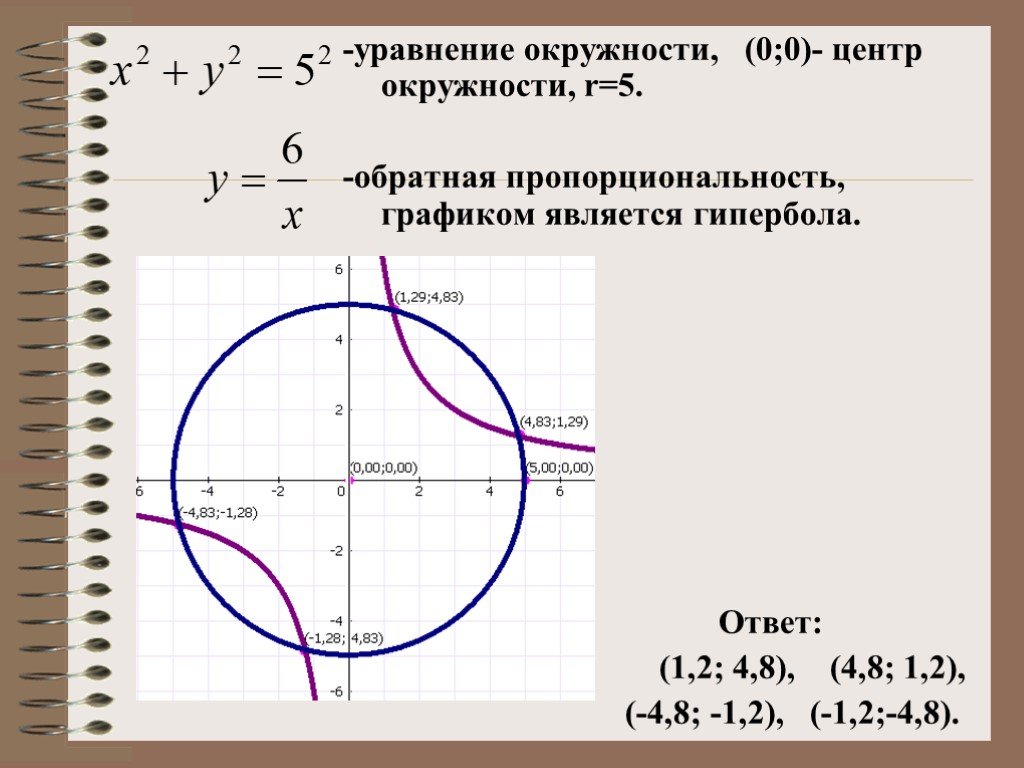 В какой точке эта прямая пересекает ось y?
В какой точке эта прямая пересекает ось y?
Решение
Общий вид уравнения прямой y = kx + b. Подставим координаты данных точек в данное уравнение вместо xи y. Получим систему, состоящую из двух уравнений:
Решив данную систему, мы найдем значения k и b. Решить систему можно способом сложения. Для этого умножим первое уравнение на -1. Получим:
Сложив первое уравнение со вторым, получим:
Теперь, когда мы знаем значение k, найдем b, подставив k в любое из исходных уравнений системы, например, в первое, получим:
Теперь можно записать уравнение прямой, подставив значения k и b в общее уравнение прямой, получим:
.
Ответим на второй вопрос. Нам необходимо найти координаты точки пересечения прямой с осью y. Координата точки xв данном случае равна 0. Подставив в общее уравнение прямой вместо x нуль, найдем координаты точки y:
Таким образом, координаты точки пересечения прямой с осью y — (0; -5). Необходимо отметить, что если необходимо найти координаты точки пересечения прямой с осью x, y будет равен нулю.
какая основная, тригонометрические, математическая и геометрическая
Содержание:
- Что такое окружность — определение и свойства
- Через какие параметры ее можно найти
- Формула длины окружности
- Формула диаметра окружности
- Формула радиуса окружности
- Примеры задач с решением
Содержание
- Что такое окружность — определение и свойства
- Через какие параметры ее можно найти
- Формула длины окружности
- Формула диаметра окружности
- Формула радиуса окружности
- Примеры задач с решением
Что такое окружность — определение и свойства
Определение
Окружность является совокупностью множества точек, расположенных на плоскости, и равноудаленных от определенной точки О, которая представляет собой центр окружности.
Определение
Единичной окружностью называют такую окружность, радиус которой равен единице.
Определение
Круг представляет собой часть плоскости, которая ограничена окружностью.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Окружность обладает рядом характерных свойств:
- Диаметр окружности в два раза больше, чем радиус окружности: D = 2r.
- Минимальное расстояние от центра окружности к секущей (хорде) в любом случае меньше, чем радиус окружности.
- Если существуют три точки, расположенные не на одной прямой, то через них можно провести единственно возможную окружность.
- Из всех замкнутых кривых, обладающих аналогичной длиной, окружность обладает максимально возможной площадью.
- При соприкосновении пары окружностей в определенной точке, эта точка расположена на прямой, которая проходит через центры заданных окружностей.
 {2}
\)
{2}
\)Параметрическое уравнение окружности, которая имеет радиус r и центр в точке с координатами (a, b) в декартовой системе координат, записывают следующим образом:
\(\begin{cases}x = a + r cos t\\y = b + r sin t\end{cases} \)
Формула длины окружности
Определение
Длиной окружности является длина замкнутой плоской кривой, которая ограничивает круг.
Длину окружности можно определить, зная ее диаметр:
\(L = \pi D\)
При известном радиусе длину окружности можно вычислить по формуле:
\(L = 2\pi r\)
Формула диаметра окружности
Определение
Диаметр окружности D является отрезком, соединяющим пару точек окружности и проходящим через ее центр.
Существует две формулы для определения диаметра окружности через радиус и длину:
\(d = 2 * R\)
\(d = \frac{C}{\pi}\)
Формула радиуса окружности
Определение
Радиус окружности R является геометрическим расстоянием, на которое удалена любая точка окружности от ее центра О.
 {2} = 6084\)
{2} = 6084\)Ответ: площадь квадрата составляет 6084.
Задача 2
Диаметр окружности равен 5 см. Необходимо определить, какова длина заданной окружности.
Решение
Длину окружности можно рассчитать по формуле:
\(L = \pi D\)
Исходя из условий задачи, подставим значение диаметра в уравнение и выполним вычисления:
L = 3,14 * 5 = 15,7 (см)
Ответ: длина окружности равна 15,7 см.
Задача 3
Существует окружность с радиусом 3,5 м. Требуется определить длину данной окружности.
Решение
В первую очередь следует определить величину диаметра рассматриваемой окружности:
D = 2r = 3,5 * 2 = 7 (м)
Далее можно рассчитать длину окружности:
\(L = \pi D = 3,14 * 7 = 21,98 (м)\)
Ответ: длина окружности составляет 21,98 м.
Задача 4
Длина окружности составляет 7,85 м. Требуется определить радиус этой окружности.
Решение
Рассчитать радиус окружности, зная ее длину, можно путем деления длины на \(2\pi:\)
\(R = \frac{C}{2\pi}\)
Таким образом:
\(R = \frac{7,85}{2 * 3,14} = \frac{7,85}{6,28} = 1,25 (м)\)
Ответ: радиус окружности равен 1,25 м.

Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Уравнение окружности — GCSE Maths
Здесь мы узнаем об уравнении окружности , в том числе о том, как распознать уравнение окружности, составить уравнение окружности с учетом ее радиуса и центра, использовать уравнение окружности найти его центр и радиус и решить задачи.
Существуют также рабочие листы уравнения круга, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое уравнение окружности? 92, где r представляет собой радиус (с центром в точке 0,0).
Окружность — это набор всех точек на плоскости, находящихся на фиксированном расстоянии от центра. Это расстояние называется радиусом.

Для получения сертификата GCSE вам необходимо уметь распознавать и использовать уравнение окружности с центром в начале координат, поэтому рассмотрите приведенный ниже рисунок окружности на наборе осей:
Теперь рассмотрим прямоугольный треугольник, созданный, когда радиус круга является гипотенузой треугольника (см. рисунки ниже): 92 , поэтому радиус r равен 3 .
Что такое уравнение окружности?
Как пользоваться уравнением окружности
Для решения задач на уравнение окружности:
- Напишите общее уравнение окружности.
- Укажите любые известные вам переменные.
- Подставьте любые известные вам значения в уравнение.
- Используйте имеющуюся информацию для решения проблемы.
- Четко сформулируйте ответ.
Как использовать уравнение окружности
Уравнение окружности
Получите бесплатное уравнение окружности, содержащее более 20 вопросов и ответов.
 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.СКОРО
ИксУравнение окружности
Получите бесплатное уравнение окружности, содержащее более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Уравнение окружности является частью нашей серии уроков по повторению окружностей, секторов и дуг . Возможно, вам будет полезно начать с урока по основным кругам, секторам и дугам, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки этой серии включают:
- Окружности, сектора и дуги
- Сегмент окружности
- Сектор круга 9{2}=50 \\
&r=\sqrt{50} \\
&r=7,071 \quad
\end{align}\]
Четко сформулируйте ответ.
На вопрос предлагается дать ответ с точностью до 1 знака после запятой, следовательно: r=7,1
Распространенные заблуждения
- Радиус в квадрате
Помните, что в уравнении радиус показан в виде квадрата.
 Чтобы найти радиус, вам нужно извлечь квадратный корень из этого значения.
Чтобы найти радиус, вам нужно извлечь квадратный корень из этого значения.- Радиус и негативы 92=40 просмотрено
(1)
\sqrt40(1)
9 0002 (1)
2\sqrt10Контрольный список обучения
Теперь вы узнали, как:
- Определение и применение определений и свойств окружности, включая: центр, радиус, хорду, диаметр, длину окружности
- Распознавание и использование общего уравнения окружности с центром в начале координат
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе обучения математике GCSE.
2 способа начертить окружность ulus Для чайников
Предварительный расчет для чайников
Исследуйте книгу Купить на Amazon
С кругами легко работать в предварительном исчислении. Круг имеет один центр, один радиус и множество точек, но вы выполняете немного разные шаги, в зависимости от того, строите ли вы круг с центром в начале координат или вдали от начала координат.
Круг имеет один центр, один радиус и множество точек, но вы выполняете немного разные шаги, в зависимости от того, строите ли вы круг с центром в начале координат или вдали от начала координат.Первое, что вам нужно знать, чтобы построить уравнение окружности, — где на плоскости расположен центр. Уравнение окружности выглядит как ( x – h ) 2 + ( y – v ) 2 = r 2 . Это называется центр-радиус форма (или стандартная форма), потому что она дает вам обе части информации одновременно.
h и v представляют координаты центра круга, находящегося в точке ( h, v ), а r представляет радиус. В частности, ч представляет горизонтальное смещение — насколько далеко влево или вправо от оси y- находится центр круга. Переменная v представляет вертикальное смещение — насколько выше или ниже оси x- находится центр.
От центра можно отсчитать от центра r единиц (радиус) по горизонтали в обоих направлениях и по вертикали в обоих направлениях, чтобы получить четыре разные точки, все равноудаленные от центра.
 Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график окружности.
Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график окружности.Графические круги с центром в начале координат
Простейший круг для построения графика — это круг, центр которого находится в начале координат (0, 0). Потому что оба h и v равны нулю, они могут исчезнуть, и вы можете упростить стандартное уравнение окружности, чтобы оно выглядело как x 2 + y 2 = r 2 . Например, чтобы нарисовать круг x 2 + y 2 = 16, выполните следующие действия:Осознайте, что центр окружности находится в начале координат (нет h и v ) и поместите эту точку туда.
Рассчитайте радиус, найдя r.
Установить р 2 = 16. В этом случае получится р = 4.
Нанесите точки радиуса на координатную плоскость.
Вы отсчитываете по 4 в каждом направлении от центра (0, 0): влево, вправо, вверх и вниз.

Соедините точки, чтобы нарисовать круг, используя плавную круглую кривую.
Рисование окружности с центром в начале координат
На рисунке показан этот круг на плоскости.
Графические круги с центром вдали от исходной точки
Хотя графически рисовать круги в начале координат проще всего, очень немногие графы столь же прямолинейны и просты, как эти. В предварительном исчислении вы работаете с преобразованием графиков всех форм и размеров. К счастью, все эти графики построены по одной и той же схеме для горизонтального и вертикального смещения, так что вам не нужно запоминать множество правил.Не забывайте, что координаты центра круга имеют противоположные знаки ч и v из скобок в уравнении. Поскольку h и v находятся внутри символов группировки, это означает, что сдвиг происходит противоположно тому, что вы думаете.
Например, выполните следующие шаги, чтобы построить график уравнения ( x – 3) 2 + ( y + 1) 2 = 25:Найдите центр круга по уравнению ( h, v ).

( х – 3) 2 означает, что координата центра x- положительна 3.
( y + 1) 2 означает, что координата центра y- отрицательна 1.
Поместите центр круга в (3, –1).
Рассчитайте радиус, найдя r.
Установите r 2 = 25 и квадратный корень с обеих сторон, чтобы получить r = 5.
Нанесите точки радиуса на координатную плоскость.
Считайте 5 единиц вверх, вниз, влево и вправо от центра в (3, –1). Этот шаг дает вам очки в (8, –1), (–2, –1), (3, –6) и (3, 4).
Соедините точки на графике круга с помощью круглой плавной кривой.
Рисование окружности без центра в начале координат
На рисунке показано визуальное представление этого круга.
Об этой статье
Эта статья из книги:
- Предварительный расчет для чайников,
Об авторе книги:
Мэри Джейн Стерлинг изучала алгебру, бизнес-вычисления, геометрию и конечную математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет.


 и на промежутке (рис. 6.5).
и на промежутке (рис. 6.5). Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км.
Найдем ординату этой точки. Она равна 25. Получили, что за 50 мин. яхта пройдет 25 км. Аналогично, за 120 мин. яхта пройдет 35 км. {2}
\)
{2}
\) {2} = 6084\)
{2} = 6084\)

 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы. Чтобы найти радиус, вам нужно извлечь квадратный корень из этого значения.
Чтобы найти радиус, вам нужно извлечь квадратный корень из этого значения.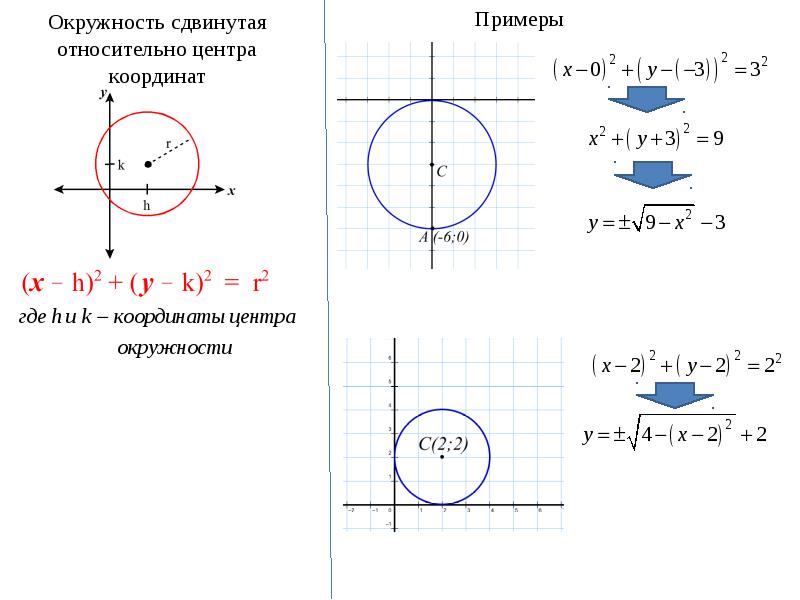 Круг имеет один центр, один радиус и множество точек, но вы выполняете немного разные шаги, в зависимости от того, строите ли вы круг с центром в начале координат или вдали от начала координат.
Круг имеет один центр, один радиус и множество точек, но вы выполняете немного разные шаги, в зависимости от того, строите ли вы круг с центром в начале координат или вдали от начала координат. Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график окружности.
Соедините эти четыре точки с лучшей кривой, которую вы можете нарисовать, чтобы получить график окружности.

