Сообщить об ошибке
Площадь поверхности куба: Формула и примеры
Давайте узнаем, как определить площадь поверхности куба .
Что такое куб?Единственный правильный шестигранник, куб представляет собой трехмерный объект с шестью квадратными поверхностями или сторонами одинакового размера, 12 ребрами и 8 вершинами. Учитывая, что его квадратные стороны равны, отсюда следует, что длина, ширина и высота куба также равны. Примерами объектов в форме куба являются игральные кости, шкатулки для драгоценностей, кубики льда, кубики сахара и кубики Рубика.
Вот иллюстрация куба. Обратите внимание, как в развернутом виде он образует 6 равных квадратных поверхностей или сторон. Получающаяся двумерная форма, когда куб разворачивается, называется сетью куба .
Как найти площадь поверхности куба : Напомним, что площадь поверхности трехмерной фигуры относится к общей площади, занимаемой поверхностью фигуры.
Чтобы лучше понять площадь поверхности, посмотрите на сеть или плоскую компоновку куба на иллюстрации ниже.
Площадь поверхности куба , равная , равна сумме площадей всех его шести квадратных сторон. Напомним, что площадь квадрата вычисляется путем умножения длины каждой стороны ( на ) на себя: на или на ². Просто умножьте площадь стороны квадрата на 6, и вы получите площадь поверхности куба.
Используйте эту формулу, чтобы найти общую площадь поверхности куба: SA = 6 a ²
, где a = длина одной стороны куба и a ² = площадь одной квадратной стороны куба.
Примечание: Не забывайте, что площади поверхности измеряются в квадратных единицах, таких как см 2 , м 2 , км 2 и 2 .
Краткое руководство по нахождению площади поверхности куба : Шаг 1.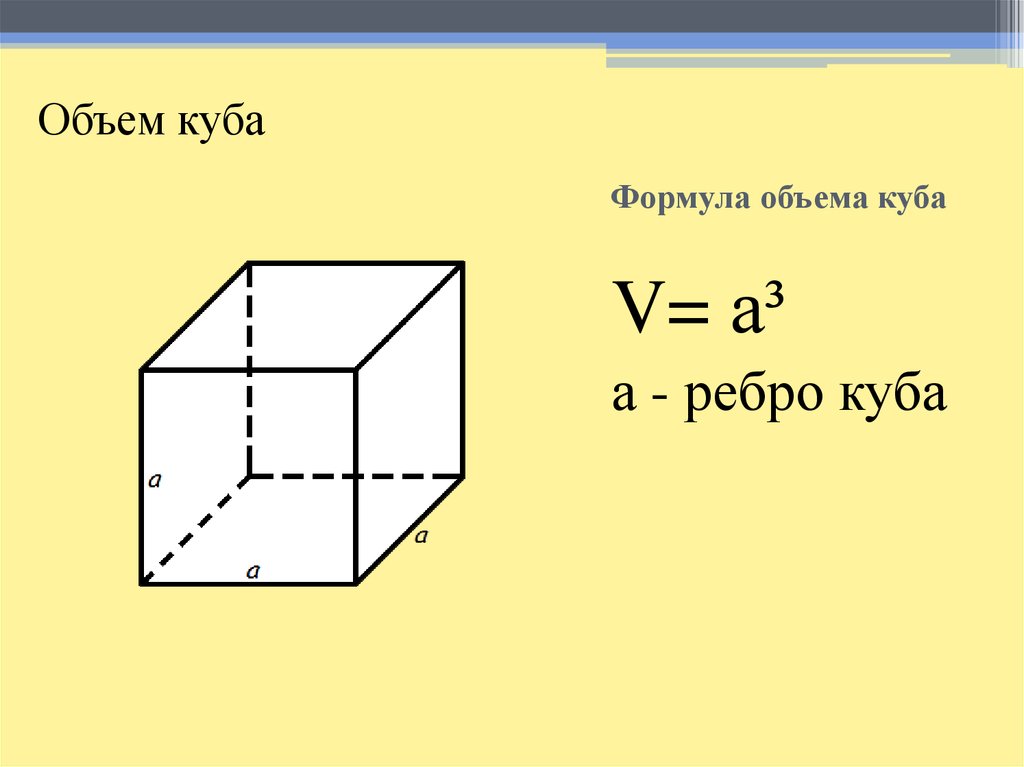
Запишите данные числа. Вам понадобится длина стороны куба, чтобы найти площадь поверхности. Убедитесь, что все единицы измерения одинаковы. Если нет, преобразуйте любой из них, чтобы он соответствовал другому.
Шаг 2. Подставьте цифры в формулу.
Шаг 3. Выполните операции. Не забудьте указать квадратную единицу площади поверхности.
Пример #1:
Найдите площади поверхности куба ниже.
Решение для примера №1:
Шаг 1. Запишите данное измерение, a = 8 м .
Шаг 2. Подставьте 8m вместо a в формуле для площадь поверхности .
SA = 6 a ²
SA = 6(8m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(64 м²)
SA = 384 м²
Таким образом, площадь равна 384 м² .
Хотите узнать, как найти объем этого куба?
Связанные материалы: Объем куба – формула и примеры
Найдите площади поверхности куба длиной 4 метра.
Шаг 1. Запишите данное измерение, a = 4м .
Шаг 2. Замените 4 м на a в формуле для площади поверхности .
SA = 6 a ²
SA = 6(4m)²
Шаг 3. Упростите и решите уравнение.
SA = 6(16м²)
SA = 96 м²
Следовательно, площадь поверхности равна 96 м² .
Спасибо, что прочитали. Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади поверхности куба .
Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!
Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus AB 2021 !Нажмите здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP Calculus BC 2021 !Что такое куб? Определение, формула, форма, свойства, примеры
Что такое куб?
Куб представляет собой твердое тело с шестью квадратными гранями.
Каждая квадратная грань имеет одинаковую длину стороны и, следовательно, все грани имеют одинаковый размер.
Куб имеет 12 ребер и 8 вершин. Каждая вершина относится к углу, где встречаются три ребра куба.
Мы можем наблюдать несколько примеров формы куба в нашей повседневной жизни. Объекты в форме куба включают в себя кубики сахара, игральные кости, кубики льда и всемирно известный кубик Рубика!
Давайте изучим свойства и роль куба в математике и в реальной жизни.
Свойства формы куба
- Это трехмерная фигура квадратной формы
- Она имеет 6 граней, 12 ребер и 8 вершин
- Все грани имеют форму квадрата
- Все стороны имеют одинаковой длины
- Каждая вершина пересекает три грани и три ребра
- Ребра параллельны ей
- Все углы куба прямые
Площадь поверхности куба
Общая площадь поверхности куба определяется как площадь его внешней поверхности.
Поскольку у куба шесть квадратных граней и все квадратные грани имеют одинаковый размер, общая площадь поверхности куба = 6 ✕ площади одной грани.
Допустим, длина каждого ребра равна «a».
Площадь одной квадратной грани = ребро ✕ ребро = a ✕ a = a ²
Следовательно, общая площадь поверхности куба = 6a ²
Общая площадь поверхности куба будет равна сумме всех шести граней куба.
Площадь боковой поверхности куба
Представьте, что вы сидите в комнате в форме куба. Затем вы можете увидеть четыре стены вокруг вас. Это обозначает площадь боковой поверхности этой комнаты. То есть площадь боковой поверхности комнаты в форме куба равна площади ее четырех стен, исключая потолок и пол.
Площадь боковой поверхности куба равна сумме площадей его квадратных граней, исключая площади верхней и нижней граней.
Таким образом, площадь боковой поверхности куба = сумма площадей 4 граней = 4a²
Объем куба
Объем трехмерного объекта можно определить как его емкость или количество жидкости, которое он может вместить если бы он был полый изнутри.
Объем рассчитывается путем умножения длины, ширины и высоты объекта. В случае куба длина, ширина и высота имеют одинаковую длину. Обозначим его буквой «а».
Следовательно, объем куба равен a ✕ a ✕ a = a³
Решенные примеры
Пример 1 : Каждая сторона куба равна 20 см. Какова площадь поверхности куба?
Решение : Воспользуемся формулой для расчета площади поверхности, где значение каждой стороны равно a.
Площадь поверхности куба = 6 а² = 6 ✕ 400 = 2400 см²
Пример 2 : Каждая сторона куба равна 10 см. Каков объем куба?
Решение : Воспользуемся формулой для вычисления объема куба, где каждая сторона равна а.
Объем куба = a³ = 10 × 10 × 10 = 1000 см³
Пример 3: Кубический контейнер со стороной 2 м должен быть окрашен. Какова общая площадь окрашиваемой поверхности?
Решение : Поскольку каждая сторона равна 2 м, мы будем использовать формулу 6 ✕ (Сторона)² Следовательно, общая площадь окрашиваемой поверхности = 6 ✕ 4 = 24 м²
Практические задачи
1
Каков объем кубического стеклянного аквариума длиной 6 дюймов?
216 дюймов³
36 дюймов³
220 дюймов³
360 дюймов³
Правильный ответ: 216 дюймов³
Длина каждого края кубического аквариума = 6 дюймов.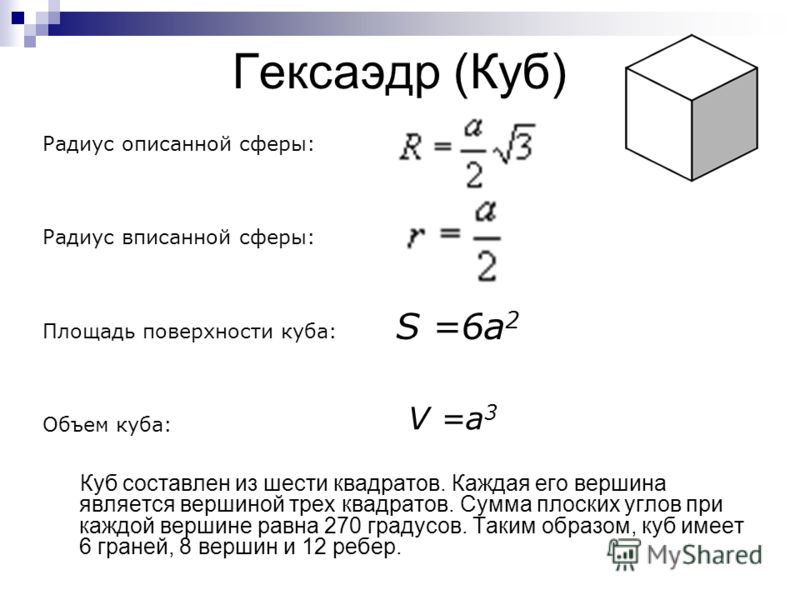
Формула объема куба = a³, где a — длина каждого ребра куба.
Следовательно, объем данного куба = 6 ✕ 6 ✕ 6 = 216 дюймов³
2
Какова общая площадь поверхности куба, если длина его ребра равна 30 см?
7200 см²
5400 см²
900 см²
1100 см²
Правильный ответ: 5400 см² axa = 900
Следовательно, общая площадь поверхности куба = 6a² = 5400 см²
3
Какова площадь боковой поверхности куба, длина стороны которого равна 6 дюймов?
36 см²
144 см²
148 см²
196 см²
Правильный ответ: 144 см²
Площадь боковой поверхности куба равна сумме площадей его квадратных граней без учета площади верхней и нижней лицо.
Таким образом, площадь боковой поверхности куба = сумма площадей 4 граней = 4a²
Площадь поверхности одной квадратной грани = a² = 36
Площадь боковой поверхности равна сумме площадей 4 граней = 4a² = 144 см²
Часто задаваемые вопросы Вопросы
В чем разница между кубом и квадратом?
Ключевое отличие состоит в том, что квадрат — это двумерный объект, а куб — трехмерный.