Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?
- Она говорит, имеются ли действительные результаты.
- Она помогает их высчитать.
- Если оно положительное, то можно найти два корня в области действительных чисел.
(1/2). - Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
- Подстановка полученного результата в исходное равенство для проверки.
- многочлен раскладывается в разность квадратов при отрицательном свободном члене;
- при положительной константе действительных решений найти нельзя.
- Если D>0 получаем два вещественных корня \displaystyle x_1=\frac{-b-\sqrt{D}}{2a} и \displaystyle x_2=\frac{-b+\sqrt{D}}{2a}.
- Если D=0 корни будут совпадать: \displaystyle x_1=x_2=\frac{-b}{2a}
- Если D<0, вещественных корней нет, но есть мнимые корни или так называемые комплексные корни (обычно изучаются в курсе математического анализа в ВУЗах, хотя иногда и встречаются в алгебре 9-11 классов).
- Пусть коэффициент a=0, тогда уравнение сводится к линейному уравнению вида kx+b=0 и уже не будет считаться неполным.
- Если равны нулю два коэффициента: и , тогда . Решением такого уравнения будет: .
- Если равен нулю коэффициент b, то имеем D=-4ac и \displaystyle x_1= \frac{\sqrt{D}}{2a} и \displaystyle x_2= -\frac{\sqrt{D}}{2a}. 2-4ac$, но я хочу знать, как это делает дискриминант. Как мы можем просто подставить коэффициенты в дискриминант и получить ответ для $k$? Как все это работает? Любой общий обзор был бы замечательным.
- алгебра-предварительное исчисление
$\endgroup$
2
Дискриминант не может определить значение $k$. Что он может сделать, так это сказать вам, сколько действительных корней будет иметь функция. Если дискриминант положителен, то он будет иметь два различных действительных корня; если оно равно $0$, то оно будет иметь два одинаковых действительных корня, а если оно отрицательное, то у функции нет действительных корней. 92 — 4ac}}{2a}$$
Обратите внимание, что если дискриминант положительный, то мы извлекаем положительный квадратный корень из числа. Двумя реальными решениями будут то, что мы получим, когда добавим значение и вычтем его ($\pm$).
Если это $0$, то у нас не может быть двух разных решений, потому что $a — 0 = a + 0$.
Если оно отрицательное, то, очевидно, реальных решений нет, потому что квадратный корень из отрицательного числа не реален.
$\endgroup$ 92=Д$.$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Найдите значение k в квадратном уравнении
Квадратное уравнение:
Стандартная форма квадратного уравнения:
ax 2 + bx + c = 0
(где a, b, c — действительные числа, а a ≠ 0)
Мы можем найти корни квадратного уравнения по формуле
x = [-b ± √(b 2 — 4ac)]/2a
Здесь b 2 — 4ac называется дискриминант (обозначается D) квадратного уравнения, решает природа корней следующая.
Д = б 2 – 4ac
Найти значения k такой, что:
Пример 1:
kx 2 + 12x + 2 = 0 имеет повторяющийся корень
Решение :
Дано, kx 2 + 12x + 2 = 0
Путем сравнения оси 2 + bx + c = 0 в данном уравнении получаемЗдесь a = k, б = 12, а c = 2
Поскольку корни действительны и равны, то D = 0
b 2 – 4ac = 0
(12) 2 – 4(k)(2) = 0
144 – 8k = 0
-8k = -144
к = 144/8
к = 18
Таким образом, значение k равно 18
Пример 2:
3x 2 + 16x + k = 0 имеет повторяющийся корень
Решение :
Дано, 3x 2 + 16x + k = 0
Путем сравнения ax 2 + bx + c = 0 в данном уравнении получаем
Здесь a = 3, б = 16, а c = k
С корнем действительны и равны, то D = 0
b 2 – 4ac = 0
(16) 2 – 4(3)(k) = 0
256 – 12k = 0
-12k = -256
к = (256)/12
к = 64/3
Написав смешанная дробь, получаем
к = 21 1/3
Итак, значение k равно 21 1/3
Пример 3:kx 2 + 6x — 3 = 0 имеет два различных действительных корня
Решение:
Дано, кх 2 + 6x — 3 = 0
Путем сравнения оси 2 + bx + c = 0 в данном уравнении получаем
Здесь a = k, б = 6 и в = -3
С корнями вещественны и различны, то D > 0
b 2 – 4ac > 0
(6) 2 – 4(k)(-3) > 0
36 + 12k > 0
12k > — 36
k > -36/12
k > -3
Итак, решение k равно k > -3, k ≠ 0
Пример 4 :
4x 2 — 12x + k = 0 имеет два различных действительных корня
Решение :
Дано, 4x 2 — 12x + k = 0
Путем сравнения ax 2 + bx + c = 0 в данном уравнении получаем
Здесь a = 4, б = -12, а c = k
Поскольку корни действительное и равное, тогда D > 0
b 2 – 4ac > 0
(-12) 2 – 4(4)(k) >
0144 – 16k > 0
-16k > -144
k < (144)/16
k < 9
Итак, решение k равно k < 9
Пример 5:
2x 2 — 5x + k = 0 не имеет действительных решений
Решение :
Дано, 2x 2 — 5x + k = 0
Сравнивая ax 2 + bx + c = 0 в данном уравнении получаем
Здесь a = 2, б = -5, а c = k
Так как корни недействительно, тогда D < 0
b 2 – 4ac < 0
(-5) 2 – 4(2)(k) < 0
25 – 8k < 0
-8k < -25
k > 25/8
Написав смешанную дробь, получаем
k > 3 1/8
Итак, решение k равно k > 3 1/8
Пример 6:
kx 2 — 11x — k = 0 не имеет действительных корней.
(1/2).Некоторые частные случаи
В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:
Если свободный член нулевой, то корни будут {0; -j}
Но есть и другие частные случаи, упрощающие нахождение решения.
Приведенное уравнение второй степени
Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k».
2 + 18 * i * j * k * m.
Допустим, дискриминант превосходит ноль. Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D < 0, то два корня комплексно-сопряженные, которые дают отрицательное значение при возведении в квадрат, а также один корень — вещественный.
Видео
Наше видео подробно расскажет о вычислении дискриминанта.
Дискриминант для решения квадратных уравнений и нахождения корней
Главная » 8 класс. Алгебра. » Дискриминант — определение, свойства, геометрический смысл
Автор Ольга Андрющенко На чтение 7 мин. Просмотров 697 Опубликовано
Важная характеристика квадратных уравнений — их дискриминант. По значению этой величины определяют, сколько корней у данного уравнения и есть ли они.
В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения — через дискриминант.
Формула вычисления дискриминанта известна
Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.
Содержание
Определение
Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.
Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.
По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.
Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.
Обозначается дискриминант квадратного уравнения буквой или знаком Δ.
Неполное квадратное уравнение
Неполным называется такое квадратное уравнение, когда один из коэффициентов такого уравнения равен нулю.
2+bx+c=0. Вычисляем дискриминант по известной формуле. Затем определяем корни уравнения.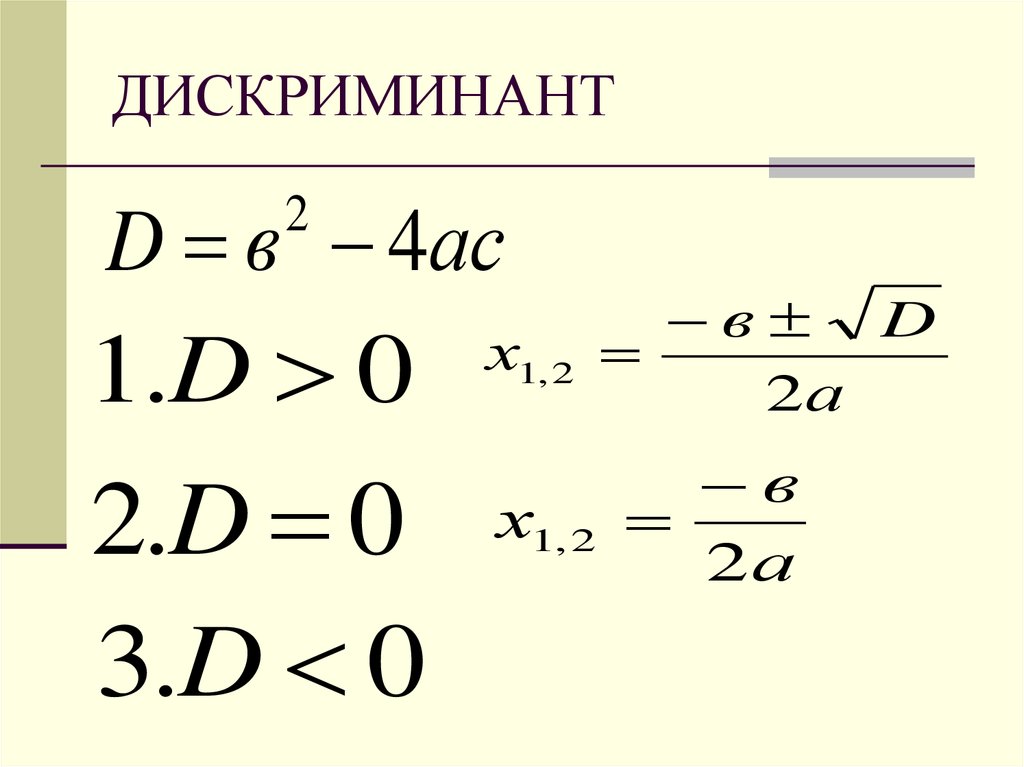
2-4ac$, но я хочу знать, как это делает дискриминант. Как мы можем просто подставить коэффициенты в дискриминант и получить ответ для $k$? Как все это работает? Любой общий обзор был бы замечательным.
