Как найти диаметр наибольшей вписанной окружности. Как найти и чему будет равна длина окружности
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы.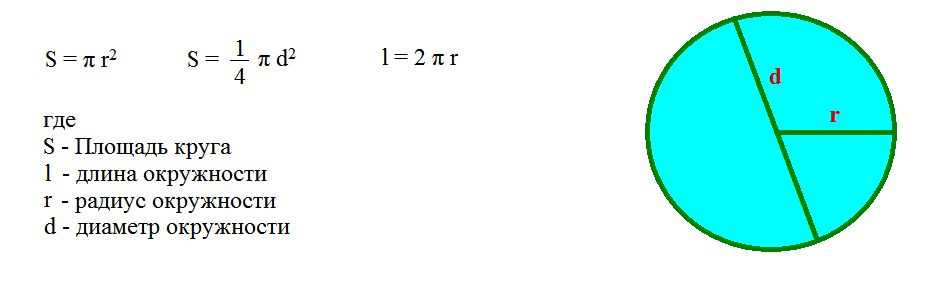 Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы.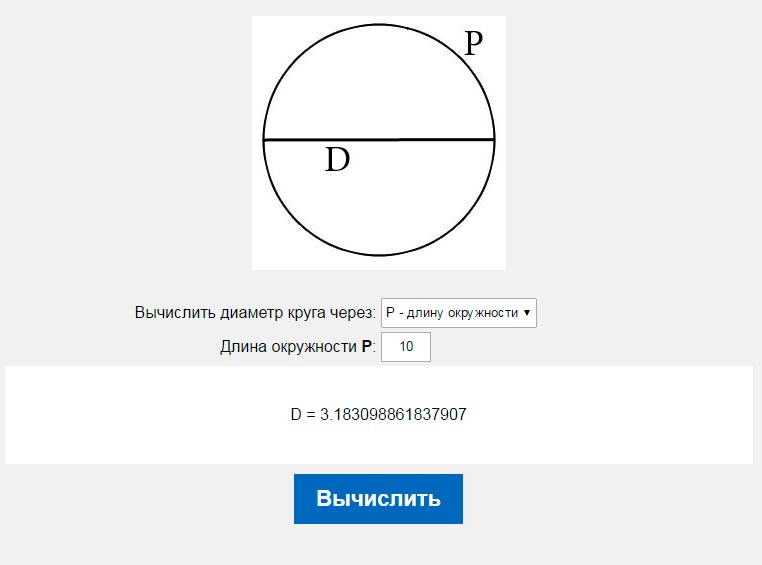 Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
- Архимед
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной.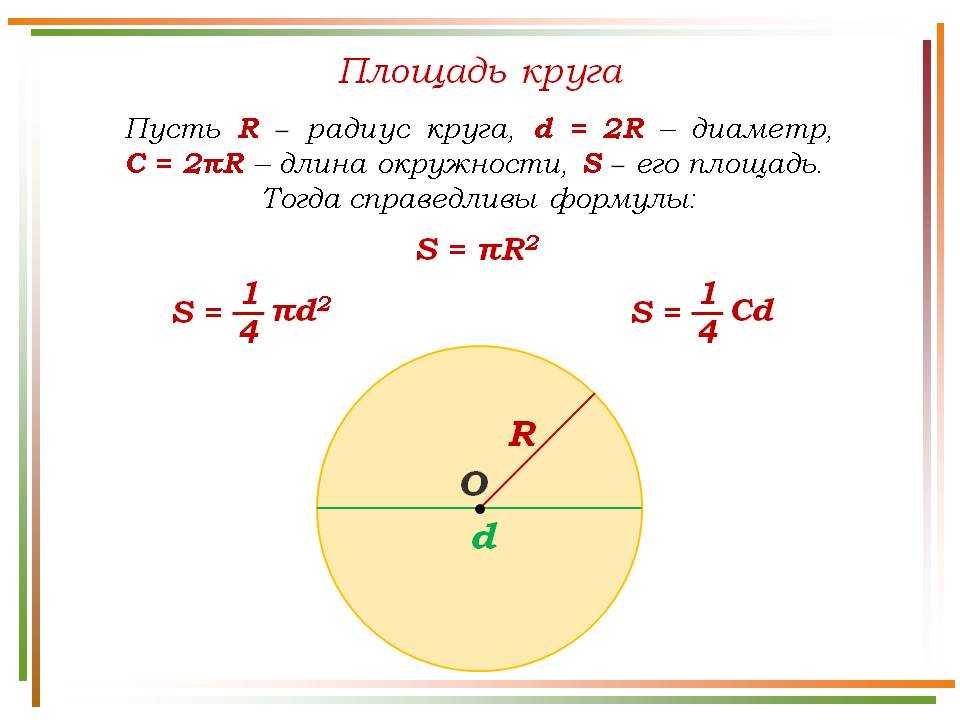 Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .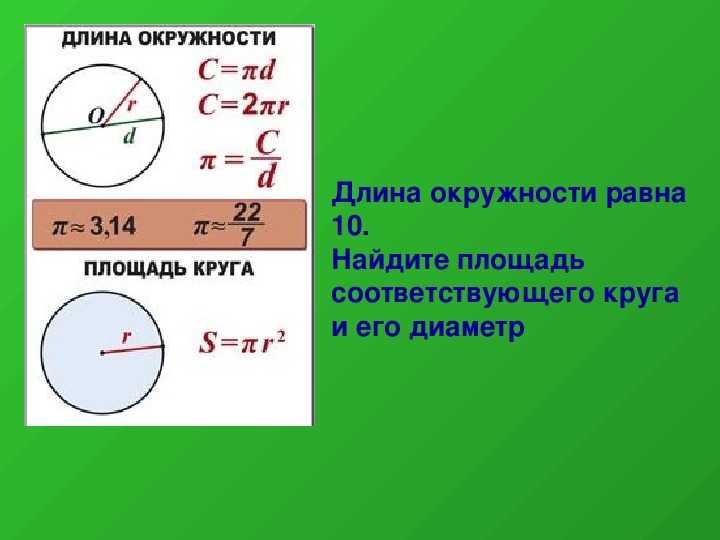
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R).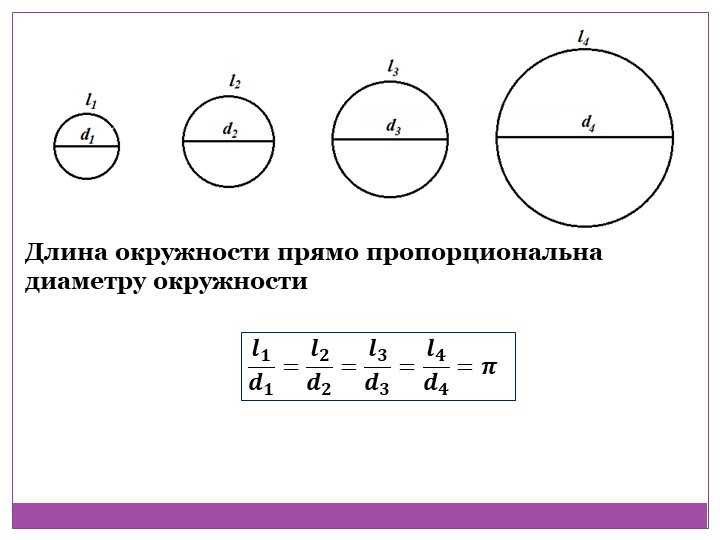 Получается: d=2R.
Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных. Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой.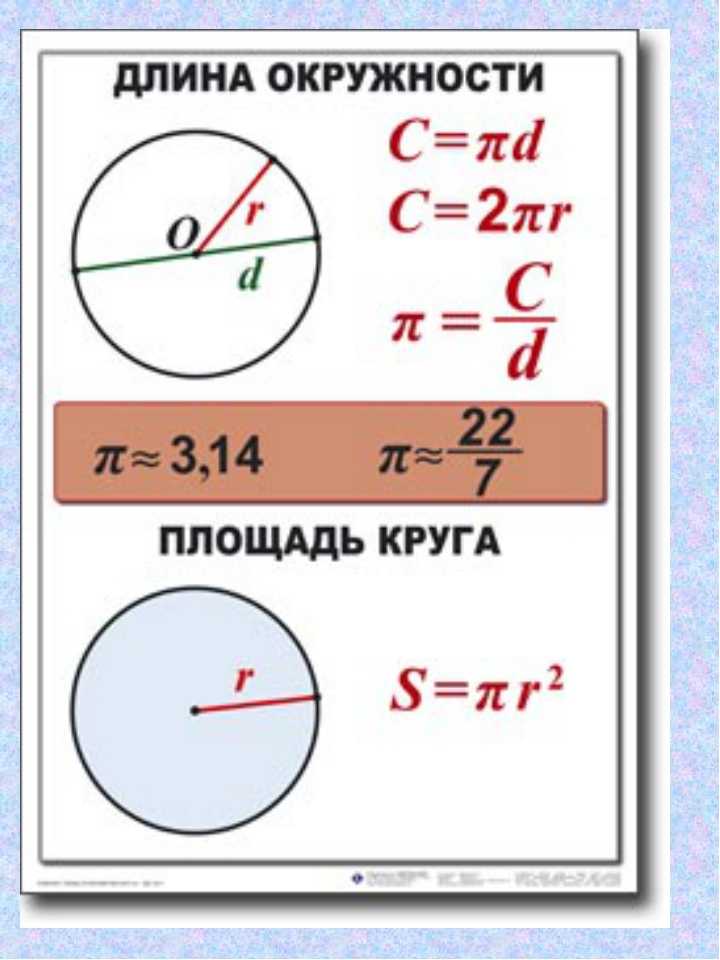 Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.
Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.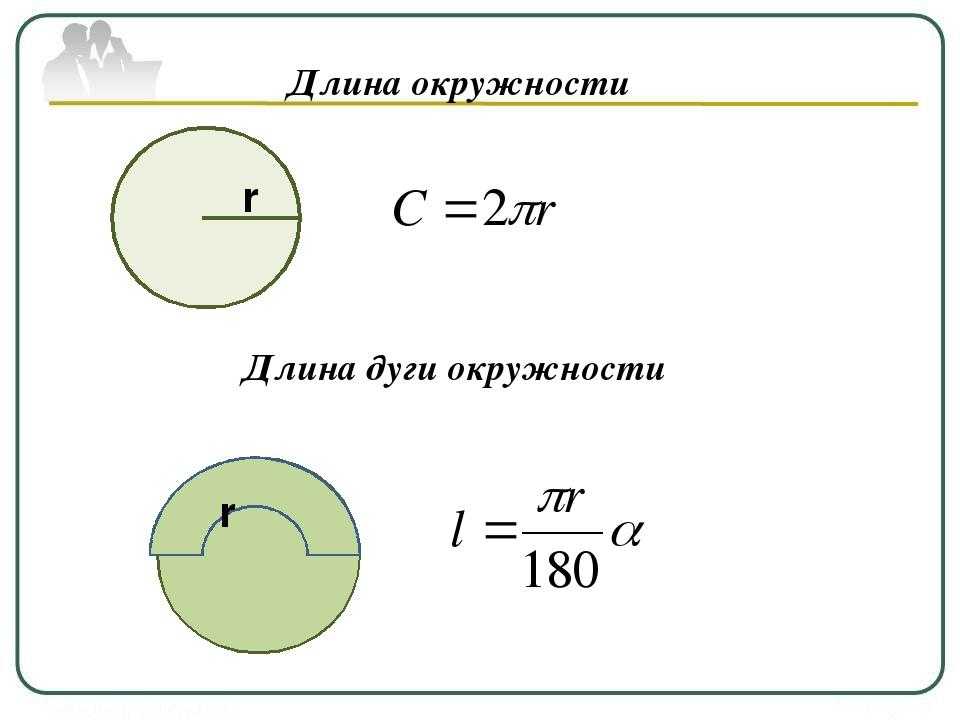
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры.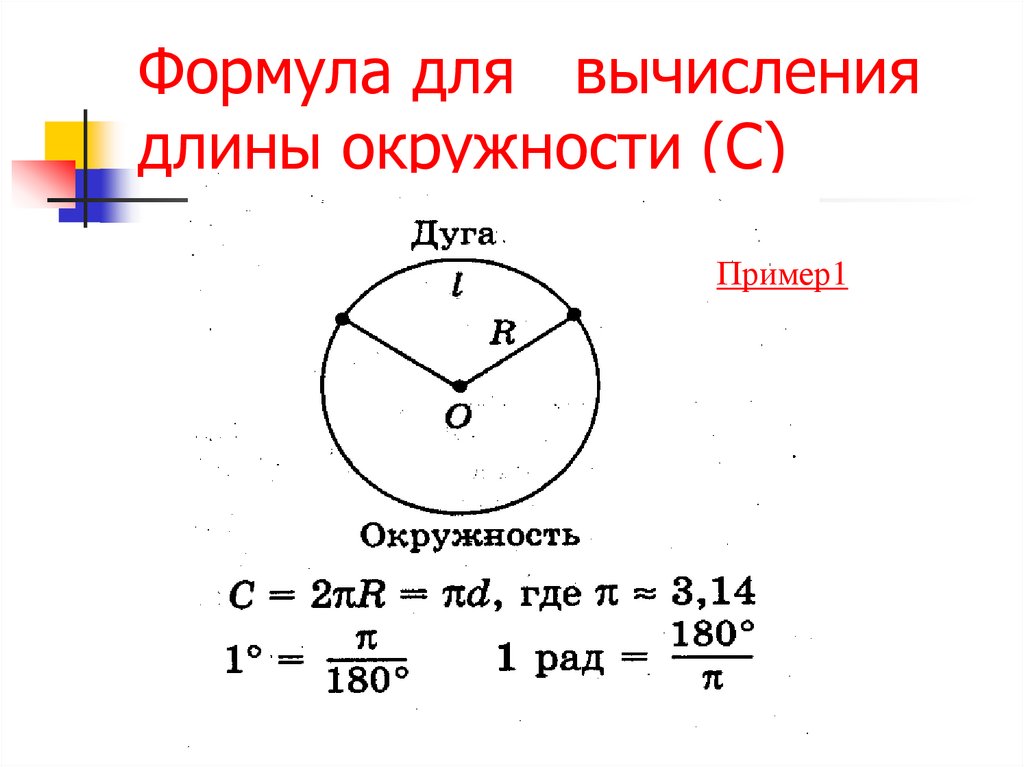 {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Формула длины окружности по диаметру. Составление системы уравнений
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O
», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π
и диаметра окружности.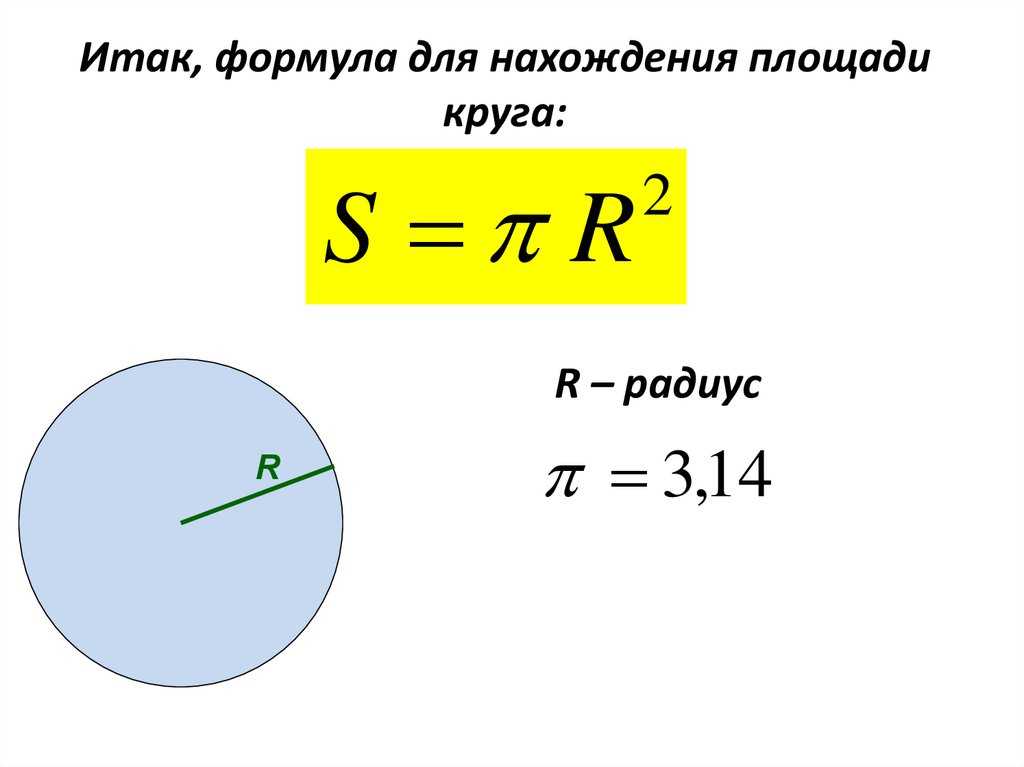 Длина окружности обозначается буквой «С
» (читается как «Це»).
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A
» и «B
». Эти точки делят окружность
на две части, каждую из которых называют дугой . Это синяя дуга «AB
» и черная дуга «AB
».
Точки «A
» и «B
» называют концами дуг .
Это синяя дуга «AB
» и черная дуга «AB
».
Точки «A
» и «B
» называют концами дуг .
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга.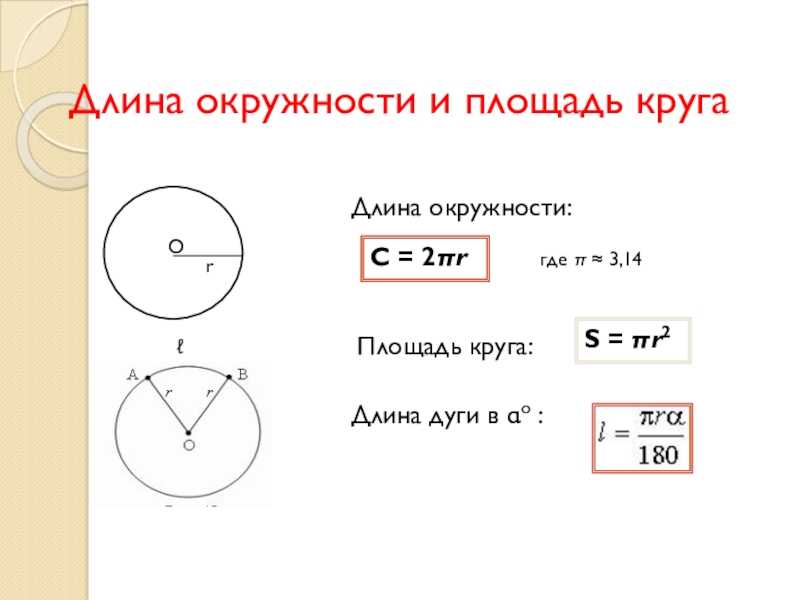 В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.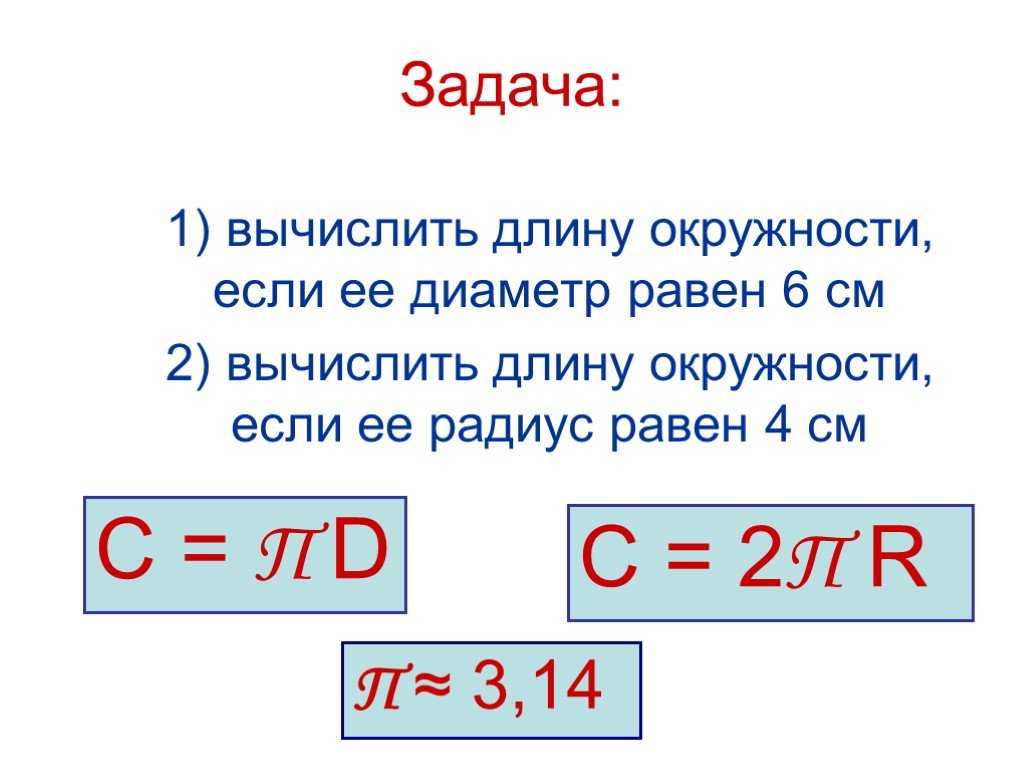
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
через диаметр и радиус. Терминология, основные формулы и характеристика фигуры.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L
, лежащей на окружности, действует равенство OL=R
. {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
В какой бы сфере экономики человек ни трудился, вольно или невольно он пользуется математическими знаниями, накопленными за многие столетия. С устройствами и механизмами, содержащими окружности, мы сталкиваемся ежедневно. Круглую форму имеет колесо, пицца, многие овощи и фрукты в разрезе образуют круг, а также тарелки, чашки, да и многое другое.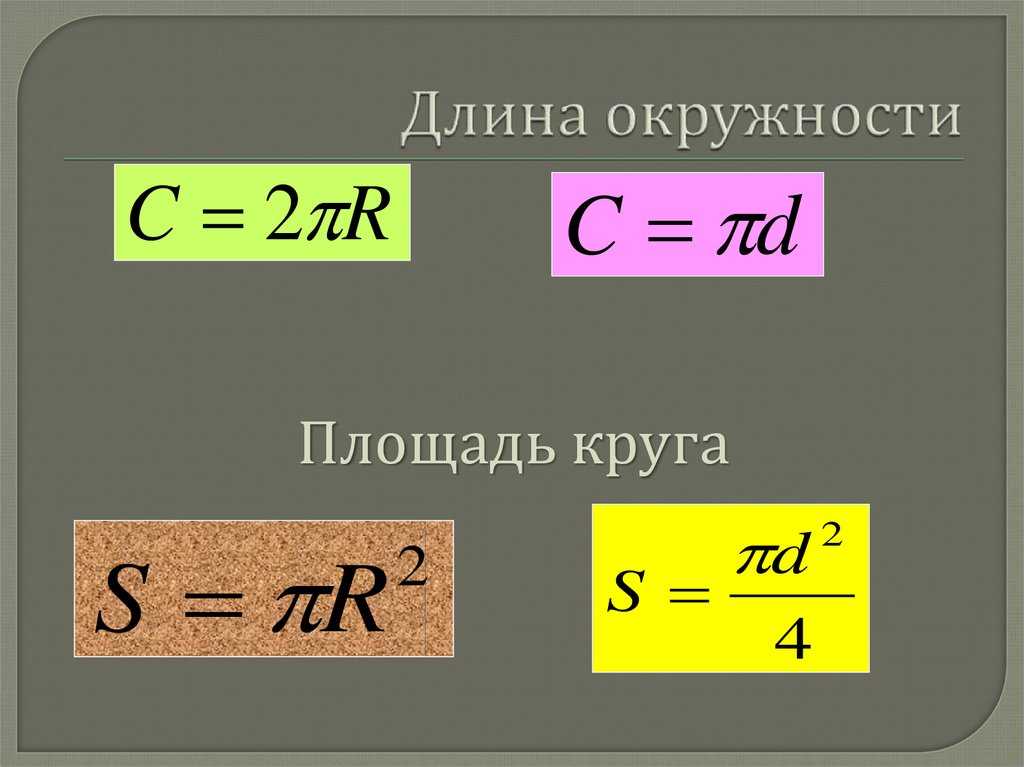 Однако, правильно рассчитывать длину окружности умеет не каждый.
Однако, правильно рассчитывать длину окружности умеет не каждый.
Чтобы вычислить длину окружности, необходимо вначале вспомнить, что такое окружность. Это множество всех точек плоскости, равноудаленных от данной. А круг – это геометрическое место точек плоскости, находящееся внутри окружности. Из вышесказанного следует, что периметр круга и длина окружности – это одно и то же.
Способы нахождения длины окружности
Помимо математического способа нахождения периметра круга, есть и практические.
- Взять веревку или шнур и обернуть один раз вокруг.
- Затем веревку измерить, полученное число и будет длиной окружности.
- Прокатить круглый предмет один раз и посчитать длину пути. Если предмет очень небольшой, можно несколько раз обмотать его бечевкой, затем размотать нить, измерить и поделить на число витков.
- Найти требуемую величину по формуле:
L = 2πr = πD ,
где L — искомая длина;
π — константа, приблизительно равна 3,14 r — радиус окружности, расстояние от ее центра до любой точки;
D – диаметр, он равен двум радиусам.
Применение формулы, чтобы найти длину окружности
- Пример 1. Беговая дорожка проходит вокруг окружности радиусом 47,8 метров. Найти длину данной беговой дорожки, приняв π = 3,14.
L = 2πr =2*3,14*47,8 ≈ 300(м)
Ответ: 300 метров
- Пример 2. Колесо велосипеда, обернувшись 10 раз, проехало 18,85 метра. Найти радиус колеса.
18,85: 10 =1,885 (м) — это периметр колеса.
1,885: π = 1,885: 3,1416 ≈ 0,6(м) – искомый диаметр
Ответ: диаметр колеса 0,6 метра
Удивительное число π
Несмотря на кажущуюся простоту формулы, почему-то многим трудно ее запомнить. Видимо, это происходит из-за того, что в формуле есть иррациональное число π, которое не присутствует в формулах площади других фигур, например, квадрата, треугольника или ромба. Нужно просто запомнить, что это константа, то есть постоянная, означающая отношение длины окружности к диаметру. Около 4 тысяч лет назад люди заметили, что отношение периметра круга к его радиусу (или диаметру) одинаково для любых окружностей.
Древние греки приближали число π дробью 22/7. Долгое время π высчитывали как среднее между длинами вписанных и описанных многоугольников в окружность. В третьем столетии нашей эры китайский математик провёл вычисление для 3072-угольника и получил приближённое значение π = 3,1416. Необходимо помнить, что π всегда постоянно для любой окружности. Его обозначение греческой буквой π появилось в 18 веке. Это первая буква греческих слов περιφέρεια — окружность и περίμετρος — периметр. В восемнадцатом веке было доказано, что эта величина иррациональна, то есть ее нельзя представить в виде m/n, где m — целое, а n – натуральное число.
В школьной математике обычно не нужна высокая точность вычислений, и π принимается равным 3,14.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре.
 Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Окружность круга: диаметр, калькулятор, формула-Embibe
- Автор Priya Wadhwa
- Последнее изменение 19-07-2022
- Автор Прия Вадхва
- Последнее изменение 19-07-2022
Окружность круга: Окружность — это замкнутая круглая форма, все точки которой равноудалены от фиксированной точки, называемой центром. Мы сталкиваемся со многими формами в нашей повседневной жизни, но круг — наиболее часто используемая форма. Обеденная тарелка, колесо обозрения, циферблат часов, поле для крикета, конфеты и руль — вот несколько примеров круглых форм, с которыми мы сталкиваемся каждый день.
Давайте поймем значение Окружности. Окружность любого объекта в математике определяет маршрут или границу, окружающую объект.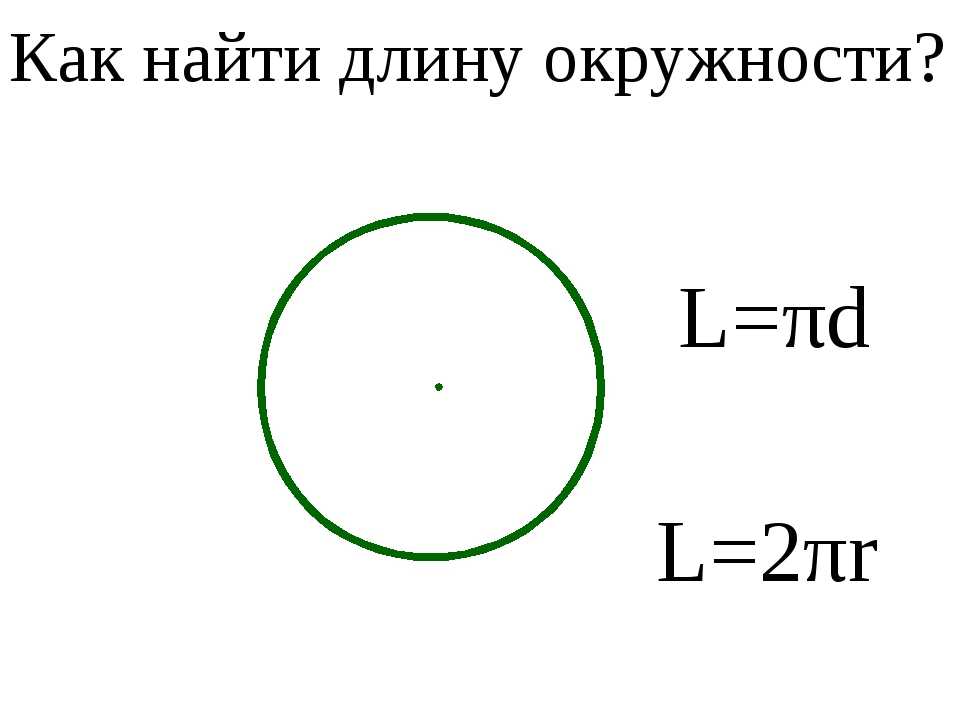 Другими словами, длина окружности также называется периметром окружности. Длина окружности измеряется в таких единицах, как метры и сантиметры. Отношение длины окружности к ее диаметру фиксировано для всех окружностей, нарисованных с любым радиусом. Это соотношение обозначается греческой буквой (пи).
Другими словами, длина окружности также называется периметром окружности. Длина окружности измеряется в таких единицах, как метры и сантиметры. Отношение длины окружности к ее диаметру фиксировано для всех окружностей, нарисованных с любым радиусом. Это соотношение обозначается греческой буквой (пи).
Изучение концепций экзамена на Embibe
Окружность круга или периметр круга — это мера длины границы круга.
Если круг разрезать с одного конца и разрезать, образуя отрезок, то его длина равна длине окружности. Обычно он измеряется в таких единицах, как \( {\text{см}}\) или \({\text{м}}\)
.Чтобы вычислить длину окружности, необходимо знать радиус или диаметр окружности.
Длина окружности: Формула
Если радиус окружности известен, то длину окружности можно рассчитать по формуле
Окружность \(= 2\pi r\)
где \(\;r\) представляет собой радиус окружности а \(\pi \) — математическая константа, значение которой примерно равно \(\frac{{22}}{7}\) или \(3. 14\) (это иррациональное число с неконечными десятичными знаками)
14\) (это иррациональное число с неконечными десятичными знаками)
Узнайте все о круге отсюда
Окружность, используемая в реальной жизни
Предположим, если кто-то хочет купить пару брюк, свитера, футболки и т. д., то необходимо рассчитать расстояние вокруг талии или груди. Поскольку наше тело не является идеальным кругом, мы должны измерить его окружность с помощью сантиметровой ленты. Этот метод обычно используется портными, чтобы найти окружность платья.
Даже часовщики должны иметь хорошие знания о кругах, поскольку они должны давать единую границу при проектировании и украшении часов.
9\circ \) тогда образуется окружность круга.
Два типа дуг могут быть сформированы в круге в зависимости от его окружности. Если дуга больше половины окружности, это большая дуга. Если она меньше половины окружности, это малая дуга.
Окружность круга диаметром
Мы знаем, что \(d = 2r.\)
Следовательно, длина окружности в форме диаметра \( = \pi \left( {2r} \right) = \pi d\)
Где d представляет собой диаметр круга
Окружность полукруга
Длина окружности полукруга равна половине длины окружности круга.
т. е. длина окружности полукруга \( = \frac{1}{2}\left( {2\pi r} \right) + 2r = \pi r + d\)
Практические экзаменационные вопросы
Как найти ширину концентрических окружностей?
Пусть \({C_1}\) и \({C_2}\) — длина окружности, а \({R_1}\) и \({R_2}\) — радиус внешней и внутренней окружности соответственно. Затем
Окружность внешнего круга \({C_1} = 2\pi {R_1}\)
\( \Rightarrow {R_1} = \frac{{{C_1}}}{{2\pi }}\)
Окружность внутренний круг \({C_2} = 2\pi {R_2}\)
\( \Rightarrow {R_2} = \frac{{{C_2}}}{{2\pi }}\)
Следовательно, ширина концентрические окружности \( = ({R_1} – {R_2}) = \frac{{{C_1}}}{{2\pi }} – \frac{{{C_2}}}{{2\pi }}\ )
Решенные примеры
Q.1. Пешеходная дорожка имеет форму кольца с внутренней окружностью \({{220}}\,{\text{m}}\) и внешняя окружность равна \({{330}}\,{\text{m}}\) Найдите ширину отслеживать. Возьмем \(\pi = \frac{{22}}{7}\)
Ответ: Пусть \({R_1}\) и \({R_2}\) — радиусы внешнего и внутреннего кольца.
Тогда \(2\pi {R_1} = 330\)
\(2 \times \frac{{22}}{7} \times {R_1} = 330\)
\(\Rightarrow {R_1} = \ frac{{330 \times 7}}{{2 \times 22}} \Rightarrow \;R = 52,5\;\text{m}\)
Теперь \(2\pi R = 220\)
\(\Rightarrow \;2 \times \frac{{22}}{7} \times R = 220\)
\(\Rightarrow {R_2} = \frac{{220 \times 7}}{{2 \ раз 22}}\)
\(\Rightarrow {R_2} = \;35\;\text{m}\)
Следовательно, ширина пешеходной дорожки \( = \left( {52,5 – 35} \right) \;\текст{м} = 17,5\;\текст{м}\)
Q.2. Длина окружности больше диаметра на \(40\;\text{см}.\) Найдите радиус окружности. Возьмем \(\pi = \frac{{22}}{7}\)
Ответ: Пусть радиус окружности \(= r\;\text{m}.\)
Тогда длина окружности \(= \;2\pi r\)
Поскольку длина окружности превышает диаметр на \(40\;\text{см}.\) Следовательно, согласно вопросу,
\(2\pi r = d + 40\)
\(\Rightarrow \;2\pi r = 2r + 40 \)
\(\Стрелка вправо \;2 \times \left( {\frac {{22}}{7}} \right) \times r = 2r + 40\)
\(\Стрелка вправо \frac{{\; 44r}}{7} – 2r = 40\)
\(\Стрелка вправо \frac{{\;\left( {44r\; – \;14r} \right)}}{7} = 40\)
\(\Стрелка вправо \frac{{\;30r}}{7} = 40\)
\(\Стрелка вправо \;r = \frac{{7 \times 40}}{{30}}\)
\( \Rightarrow \;r = \frac{{28}}{3}\;\text{см}\)
Следовательно, радиус окружности равен \(\frac{{28}}{3}\;\text {см}. \)
\)
Q.3. Радиус колес велосипеда равен \(50\;\text{см}.\) Сколько оборотов сделает каждое колесо, чтобы проехать расстояние \(157\;\text{метров}? \) Возьмите \(\pi = 3.14.\)
Ответ: Дано, радиус колес велосипеда \(\left( r \right) = \;50\;\text{см}\)
Мы знаем, что длина окружности \(= 2 \pi r\)
\(= \;2 \times 3.14 \times 50\;\text{cm}\)
\(= \;314\;\text{cm}\)
Чтобы найти количество оборотов колеса, разделите расстояние, пройденное на длину окружности колеса.
Чтобы преобразовать \(157\;\text{метры}\) в \(\text{см}\), умножьте на \(100\)
Количество оборотов \(\; = \frac{{15700}}{{ 314}} = 50\;\text{оборот}\)
Следовательно, количество оборотов, которое каждое колесо сделает, чтобы пройти расстояние \(157\;\text{метров}\), равно \(50\) оборотам.
Q.4. Кусок прямоугольной проволоки длиной \(50\;\text{см}\) и шириной \(100\;\text{см}\) отрезается и складывается в круг. Найдите длину окружности и радиус образовавшейся окружности. Возьмем \(\pi = 3,14.\)
Найдите длину окружности и радиус образовавшейся окружности. Возьмем \(\pi = 3,14.\)
Ответ: Длина окружности, образованная \(= \) периметром прямоугольного провода
Периметр прямоугольника \( = \;2\left( {L + W} \right)\)
\( = \;2\left( {50 + 100} \right)\;\text{cm} \)
\(= \;2 \times 150\;\text{см}\)
\( = \;300\;\text{см}\)
Итак, длина окружности равна \(300\ ;\text{см}.\)
Теперь вычислим его радиус.
Окружность \(= 2\pi r\)
\(300 = 2 \times \pi \times r\)
\(300 = 2 \times 3,14 \times r\)
\(300 = 6,28r\)
\(r = \frac{{300}}{{6,28}} = 47,77\;\)
Следовательно, радиус окружности равен \(47,77\;\text{см}.\)
Q.5. Тиму и его друзьям подают пиццу \(15\;дюймов\) (диаметром). Вычислите его окружность.
Ответ: Диаметр пиццы \(\left( d \right) = 15\;\text{дюймы}\)
Формула длины окружности через диаметр \(C = \pi d \)
\(C = \pi \times 15 = 15\pi \;\text{дюймы}\)
Следовательно, длина окружности пиццы равна \(15\pi \;\text{дюймы}. \)
\)
Q.6. Колесо инвалидной коляски имеет диаметр \(14\;\text{м}.\) Если колесо повернется один раз, на какое расстояние проедет инвалидная коляска?
Ответ: Если колесо сделает один оборот, кресло-коляска переместится на расстояние, равное окружности колеса.
Дан диаметр колеса \(\left( d \right) = 14\;\text{m}\)
Мы знаем, что длина окружности колеса \(C\; = \;\pi d\)
\(C = \frac{{22}}{7} \times 14\; = 44\;\text{m}\)
Таким образом, коляска движется \(44\;\text{m}\) за один оборот колеса.
Q.7. Учитывая, что радиус круга равен \(r\;\text{см}\) , и если его удвоить, то какой будет длина окружности нового круга.
Ответ: Дан радиус окружности \( = r\;\text{cm}\)
Тогда длина окружности \( = 2\pi r\)
Если радиус окружности удваивается, то новый радиус \(R = 2r\;\text{см}\)
Следовательно, длина окружности нового круга \(= 2\pi R = 2\pi \times 2r = 4\pi r\)
Следовательно, длина окружности нового круга равна \(4\pi r.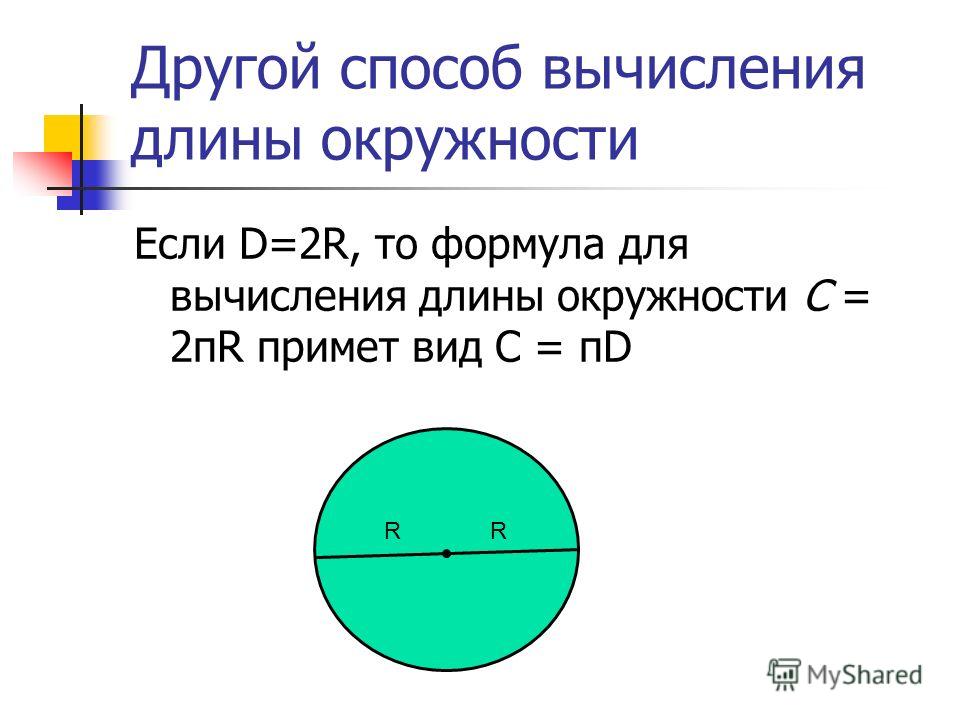 \)
\)
В.8. Келли работает в лаборатории с огромным круговым ускорителем частиц. Он имеет радиус \(6\,{\rm{метров}}\). Какова окружность акселератора?
Ответ: Дан радиус ускорителя \(= 6\;\text{m}\)
Тогда длина окружности ускорителя \(= 2\pi r\),
\(= 2\pi \times 6 = 12\pi \)
Следовательно, длина окружности ускорителя равна \(12\pi .\)
Q.9. Из круглого листа радиусом \(5\;\text{см},\) удален круг радиусом \(3\;\text{см}\) . Найдите длину окружности оставшегося листа.
Ответ: Дано, радиус внешнего листа \({r_1} = 5\;\text{см}\)
Радиус внутреннего листа \({r_2} = 3\;\text{ см}\)
Окружность оставшейся части \(= 2\pi \left( {{r_1} – {r_2}} \right)\)
\(= 2\pi \left( {5 – 3} \right) = 2\ pi \times 2 = 4\pi \)
Следовательно, длина окружности оставшейся части равна \(4\pi .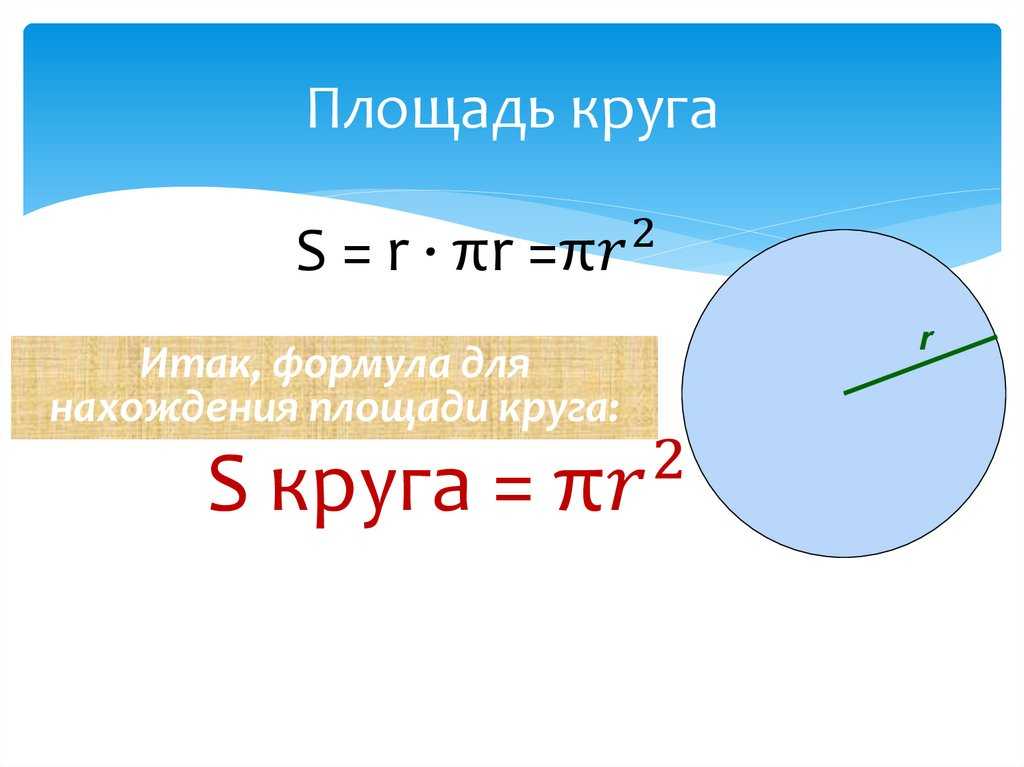 \)
\)
Q.10. Отношение радиусов двух окружностей \(4:5.\) Каково отношение их окружностей?
Ответ: Пусть радиус первой окружности \({r_1} = 4x\)
Радиус второй окружности \({r_2} = 5x\)
Отношение длины окружности двух окружностей \(= \frac{{2\pi {r_1}}}{{2\pi {r_2}}} = \frac{{4x}}{{5x}} = \ frac{4}{5}\)
Следовательно, отношение длины окружности двух окружностей равно \(4:5.\)
Попытка пробных тестов
Часто задаваемые вопросы об окружности круга
Ниже приведены часто задаваемые вопросы об окружности круга:
Q.1. Что такое окружность круга?
Ответ: Окружность круга определяется как длина вокруг его границы. Другими словами, если из круга вырезать прямую линию, то длина этой линии будет равна длине окружности.
Q.2. Почему длина окружности \(2\pi r?\)
Ответ: Рассмотрим круг диаметром d и развернём внешнюю границу или границу круга, он образует отрезок прямой линии, длина которого равна \(3\) умноженному на диаметр плюс немного больше. Тот же результат будет получен при использовании круга с чрезвычайно малым радиусом или при использовании круга с чрезвычайно большим радиусом. Следует понимать, что эта постоянная длина равна константе pi \(\left( {\pi = 3,14159…} \право).\)
Тот же результат будет получен при использовании круга с чрезвычайно малым радиусом или при использовании круга с чрезвычайно большим радиусом. Следует понимать, что эта постоянная длина равна константе pi \(\left( {\pi = 3,14159…} \право).\)
Q.3. Напишите две формулы для вычисления длины окружности?
Ответ: Есть две формулы для длины окружности
(i) Первая формула: В терминах радиуса
Если радиус окружности известен, то длина окружности равна \(2\pi r.\)
(ii) Вторая формула: В терминах диаметра
Если диаметр круга известен, то длина окружности равна \(\pi d.\)
Так как диаметр круга в два раза больше радиуса.
Q.4 . Какова общая длина окружности?
Ответ: Чтобы найти полную длину окружности, просто умножьте диаметр окружности на константу \(\pi \) (pi).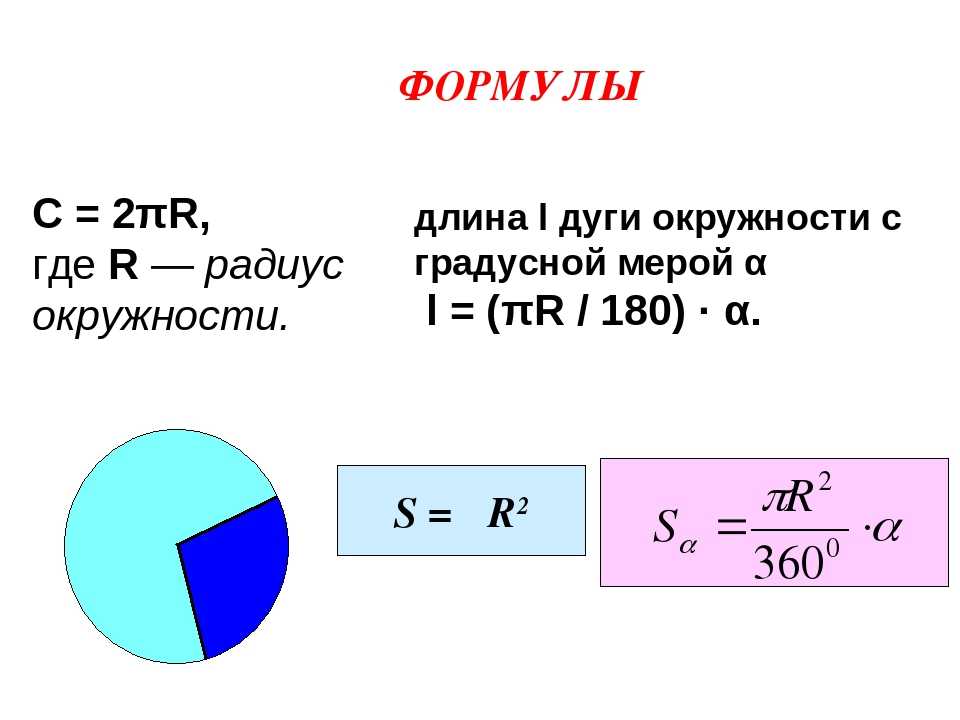 Полную длину окружности также можно найти, умножив радиус вдвое на константу pi \(\left( \pi \right).\)
Полную длину окружности также можно найти, умножив радиус вдвое на константу pi \(\left( \pi \right).\)
Q.5 . Как найти диаметр по длине окружности?
Ответ: Длина окружности \(= \;\text{Диаметр}\; \times \;\pi \)
Или диаметр \( = \frac{\text{Окружность}}{\ pi }\)
Итак, диаметр окружности в виде окружности равен отношению длины окружности к математической константе \(\pi .\)
Q.6 . Как найти радиус по длине окружности?
Ответ: Длина окружности \(= \;2\pi r\)
Или, радиус \(= \frac{\text{Окружность}}{{2\pi }}\)
Итак , радиус окружности в виде окружности равен отношению длины окружности к удвоенной математической константе \(\pi .\)
Q.7. Чем длина окружности отличается от площади круга?
Ответ: Окружность есть не что иное, как расстояние вокруг границы круга. 2\)
2\)
А длина окружности \(= 2\pi r\)
Следовательно, установить зависимость между длиной окружности окружности и ее площадью. Площадь круга равна половине радиуса, умноженного на длину окружности.
Q.9. Как найти длину окружности?
Ответ: Первый метод: Поскольку поверхность круга искривлена, мы не можем физически вычислить длину круга с помощью шкалы или линейки. Но это можно сделать для многоугольников, таких как треугольники, квадраты и прямоугольники. Вместо этого мы можем вычислить длину окружности с помощью нити. Проследите путь круга с помощью нити и отметьте точки на нитке. Теперь рассчитайте эту длину с помощью линейки.
Второй метод: Правильный способ узнать длину окружности — вычислить ее, если известны радиус или диаметр. На приведенном ниже рисунке показана окружность с радиусом \(r\) и центром \(O\). Диаметр в два раза больше радиуса окружности.
Пройдите бесплатные пробные тесты по главе Circles здесь
Также проверьте,
ICSE Class 10 Study Tips 2022: Советы по подготовке к CISCE
ICSE Class 10 Math: Syllabus, Books, Exam Pattern
Решение ICSE Class 10: скачать бесплатно PDF
ICSE Class 10 Sample Papers: скачать бесплатно PDF
Резюме
I В этой статье о длине окружности мы узнали определение, формулы и способы узнать длину окружности, а также несколько решенных примеров.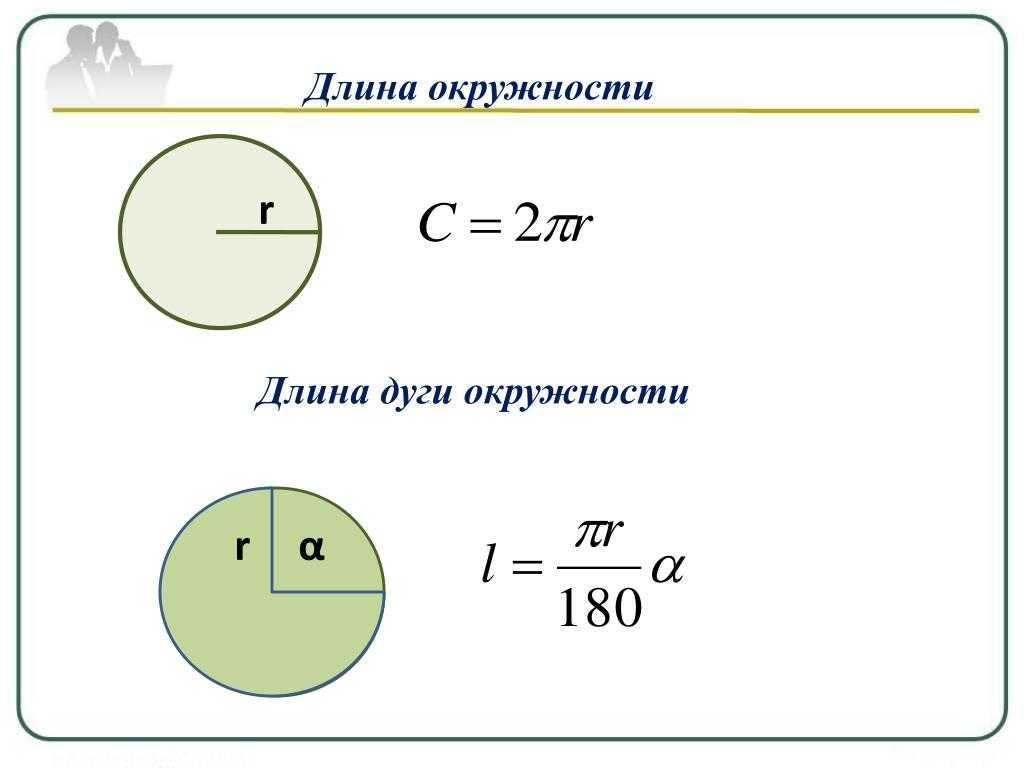 Мы надеемся, что эта подробная статья об окружности круга помогла вам. Если у вас возникнут какие-либо проблемы, связанные с этим, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время. Вы можете найти больше задач на окружность круга в ICSE Class 10 Sample Papers от Embibe.
Мы надеемся, что эта подробная статья об окружности круга помогла вам. Если у вас возникнут какие-либо проблемы, связанные с этим, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время. Вы можете найти больше задач на окружность круга в ICSE Class 10 Sample Papers от Embibe.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с Окружностью круга
Как найти периметр или длину окружности? Формула
Как найти длину окружности или периметр окружности? Это общий вопрос для всех нас, особенно для всех школьников.
Замкнутая плоская геометрическая форма — это то, что мы бы назвали по ее основному определению. Переходя к техническому языку, круг представляет собой положение точки на плоскости, которая всегда находится на постоянном расстоянии от фиксированной точки. Круги обычно называют круглыми формами с точки зрения непрофессионала.
В этой статье мы обсудим самый основной принцип длины окружности.
Множество диаграмм с примерами и пояснениями упражнений помогают понять основную концепцию.
Давайте изучим концепцию!
Как найти длину окружности
Важно отметить, что фиксированное расстояние — это радиус окружности. Окружность и площадь кругов и полукругов рассчитываются с использованием радиуса круга. Пицца, колесо и т. д. — все это примеры кругов на линии.
Здесь мы увидим, как найти длину окружности. В наших многочисленных математических вычислениях мы используем термин «периметр круга» и выполняем наши расчеты. Теперь этот периметр должен быть известен как
- . Он требуется для вычисления площади круга или цилиндра.
- Можно рассчитать длину окружности.
- Длина, на которую можно сделать круг.
Давайте перейдем к основной статье!
Периметр круга Терминология
Прежде чем понять , что такое окружность круга , мы изучим несколько терминов, связанных с кругом,
- Окружность
- Центр
- Окружность или периметр окружности
- Радиус 7 Диаметр терминология периметра окружности
- Это в два раза больше радиуса, что означает « 2r» .
- Диаметр обозначается как « d».
- Итак, мы можем написать d=2r .
- Пи – константа, равная отношению длины окружности к диаметру.
- Значение Пи равно 22/7 или 3,141592….
 . или приблизительно 3,14.
. или приблизительно 3,14. - Безразмерно.
- Обозначается греческой буквой ‘ π’ .
- Общая длина любой двумерной круглой поверхности.
- Его также называют периметром круга.

- Он передается как C .
- В случае окружности полукруга мы обычно используем « c ».
- Философия та же, что и для периметра квадратов или прямоугольников.
- r = радиус окружности
- D = диаметр
- C = окружность круга
- π = 3,14
- Если известен радиус (r)
- Если известен диаметр (D)
- Если известна площадь
- Конгруэнтные окружности имеют равные радиусы.
- Также есть сходство между кругами с разными радиусами.
- В идеале хорды, равноудаленные от центра, должны иметь одинаковую длину.
- Каждая точка на окружности одинаково удалена от центра.
- Диаметр окружности — это ее самая длинная хорда.

- Окружности делятся на равные дуги по диаметру. Каждая дуга представляет собой полуокружность.
- Если радиус любых двух окружностей в точности одинаков, то такие окружности называются конгруэнтными.
- Две или более окружностей разного радиуса, но с одним и тем же центром называются концентрическими окружностями.
- 5
9 Площадь: кольцеобразной области = 2200 кв.см.
Можете ли вы проанализировать периметр и площадь полукруга радиусом 35 см? Значение пи должно быть 22/7?
Когда мы подставляем значения в оба уравнения, мы получаем следующее:
Периметр полукруга = (π + 2) r
= π r + 2r
= 22/7 x 35 + 2 x 35
= 110 + 70
= 180 см
Площадь полукруга = (π x r2) / 2 = (22/7 x 1225) / 2 = 1925 см²
Можете ли вы рассчитать периметр круга площадью 616 квадратных футов?
Площадь круга составляет 616 кв.
 футов
футовЗатем значение подставляется в требуемое уравнение, что дает нам следующее:
Площадь = 𝜋r2
616 = 22/7 x R2
R2 = (616 * 7/22)
R2 = 28 * 7
R2 = 196
R = 14 футов
Периметр = 2 𝜋 R
Периметр = 2 x. 22/7 x 14
Периметр = 88 футов
Ответ: Периметр = 88 футов
Часто задаваемые вопросы о периметре круга
Как найти периметр круга?
Формула периметра состоит из трех компонентов: двух констант и одной переменной — радиуса. Периметр или окружность круга можно рассчитать по следующей формуле.
2 𝜋r = 𝜋D
Где r = радиус
D = диаметр.Что такое периметр и площадь круга?
Круги имеют периметр, равный их границам. В результате периметр и длина окружности равны. Круг имеет площадь 𝜋r2 и периметр 2𝜋r, когда радиус составляет r единиц и 𝜋 = 3,14 или 22/7.

Кто изобретатель круга?
Антропологи в целом согласны с тем, что круг был создан до того, как история была записана, но это не гарантируется. Греки также считали египтян изобретателями геометрии и думали, что они сделали все это возможным.
Является ли окружность периметром круга?
Длина окружности — это длина, которую она проходит за один оборот. Другой способ определить это — определить общую длину поверхности круга, которая представляет собой не что иное, как его периметр. Таким образом, периметр круга называется его окружностью.
Как найти периметр круга для детей?
Рассмотрим сценарий, в котором вы хотите знать, как далеко вы отклонились от озера. Круг образует пешеходную дорожку вокруг озера. Длина окружности используется для расчета расстояния пешеходной дорожки.
 Окружность круга — это расстояние вокруг его внешней стороны.
Окружность круга — это расстояние вокруг его внешней стороны.Можете ли вы кратко описать окружность?
Круговые точки — это те, которые движутся по плоскости таким образом, что их расстояние от фиксированной точки остается постоянным. Фиксация точки и расстояния известна как центр и радиус соответственно. (X-h)2 + (Y-k)2 = r2 — формула окружности на плоскости.
Почему периметр круга называется окружностью?
Окружность круга или эллипса от латинскогоcircferens, что означает «перенос», является его периметром. Другими словами, длина окружности была бы равна длине дуги, как если бы она была превращена в отрезок и раскрыта.
Почему периметр круга равен 2 пир?
В заключение, окружность: радиус или окружность: диаметр постоянны для каждого круга.
 Окружность = 𝜋 диаметр, или окружность = 2 𝜋 радиус, если эта константа равна числу 𝜋.
Окружность = 𝜋 диаметр, или окружность = 2 𝜋 радиус, если эта константа равна числу 𝜋.Как найти периметр круга по площади?
Периметр области определяется как расстояние вокруг нее. Рассчитайте длину забора, полностью окружающего вашу собственность. Все стороны прямоугольника складываются вместе, чтобы вычислить периметр. Круги нелегко измерить, потому что они не имеют прямых линий. Чтобы определить периметр круга с площадью, требуется специальная формула, которая равна 𝜋D или 2 𝜋r.
Можете ли вы сказать мне разницу между полукругом и кругом?
Половина круга называется полукругом. Именно диаметр определяет форму полукруга. Кроме того, радиус в два раза больше и действует как основание полукруга.
Каковы свойства полукруга?
1. Полуокружности — это замкнутые 2D-формы.

2. У него изогнутый край, что делает его не многоугольником.
3. В полуокружности есть одно изогнутое ребро, называемое его окружностью, и одно прямое ребро, называемое его диаметром.
4. В полуокружности ровно половина круга.
5. Половина радиуса круга – это площадь полукруга.Можете ли вы назвать полуокружность дугой?
Большие дуги — это дуги с размерами более 180 градусов. Поскольку полуокружность делит окружность пополам, дуга, равная 180 градусам, называется полуокружностью. По ширине круга каждая пара конечных точек определяет либо малую и большую дуги, либо две полуокружности.
У полукруга есть вершина или нет?
Помимо того, что полуокружность не имеет вершин, она также имеет пересечения кривой линии с прямой вместо двух прямых.
Заключение
Итак, мы научились находить периметр квадрата и если есть сомнения, сообщите нам.

Дальнейшее изучение, чтобы увидеть много интересных статей!
Правила употребления предлога в
Светящиеся и светящиеся предметы
Что такое отражение света
Что такое существительное в английской грамматике
Что такое магнит для детей
Квадратный корень из 2
Квадратный корень из 5
Формула окружности и калькулятор
Калькулятор окружности
Следующий калькулятор находит длину окружности на основе радиуса круга. Используемое значение π округляется до 3,14. Введите значение в поле радиуса и нажмите ‘»’ кнопка.
радиус: окружность: Наименьшее расстояние по окружности называется окружностью и его можно вычислить если радиус известен.
 Популярное уравнение требует, чтобы диаметр был известен,
что, в свою очередь, всегда удваивает радиус. Поэтому расчет всегда
уравнение с одним неизвестным:
Популярное уравнение требует, чтобы диаметр был известен,
что, в свою очередь, всегда удваивает радиус. Поэтому расчет всегда
уравнение с одним неизвестным:длина окружности = 2 * π * радиус
π = 3,14История расчета
Решение математического уравнения обычно является решением большинства проблем. с которыми сталкиваются студенты-математики. Однако в реальной жизни существуют и другие практические методы. чтобы найти длину окружности. Представьте, что вам нужно вычислить окружность круглого кольца. Очевидно, будет сложно найти точный радиус или диаметр такого и объекта. В этом случае простое решение сделать отметку на кольце и поместить его так, чтобы отметка касалась пола. затем мы ставим еще одну отметку на полу в том месте, где у нас есть отметка на кольцо. Далее достаточно раскатать кольцо до полного заполнения оборот, и след снова заканчивается прямо на полу.
 Делаем еще одну отметку в
то место на полу. Теперь мы можем просто вычислить расстояние между двумя
отметки на полу с помощью простой рулетки. Это расстояние будет равно
окружность данного кольца. Прокатывая кольцо, мы должны убедиться, что кольцо
не скользит, так как это может исказить результат измерения.
Делаем еще одну отметку в
то место на полу. Теперь мы можем просто вычислить расстояние между двумя
отметки на полу с помощью простой рулетки. Это расстояние будет равно
окружность данного кольца. Прокатывая кольцо, мы должны убедиться, что кольцо
не скользит, так как это может исказить результат измерения.Есть много реальных жизненных ситуаций, когда такой вид расчета пригодится. Простой пример — как можно узнать, сколько нужно оберточной бумаги. обернуть какой-нибудь круглый предмет: бутылку, свернутую дорожную сумку. Или как долго Лента, которую нужно обмотать вокруг футбольного мяча. Понимание принципа расчета длина окружности имеет решающее значение для понимания того, как работают спидометры, это в машине или на велосипеде. Если вы немного разнорабочий, вы можете в прошлом устанавливал спидометр на свой велосипед. Вы можете помнить, что всегда необходимо произвести базовую настройку, чтобы устройство правильно показывало скорость.
 Обычно
кроме крепления устройства к перекладине требуется подобрать размер
колеса велосипеда. Этот размер обычно указывается на самой шине в некоторых
некое стандартизированное обозначение. Это обозначение, очевидно, имеет огромное значение.
к цифровому измерителю, так как он будет использоваться для расчета расстояния, на котором
крышки с одним оборотом колеса. Датчик на перекладине определяет каждый полный оборот
и отправьте на счетчик, который дополнительно отслеживает время. Зная расстояние, которое
было пройдено, и время, которое потребовалось, счетчик вычисляет скорость, используя простой
уравнение: скорость = расстояние/время. Если мы возьмем расстояние в милях и время в
часов мы получим скорость в милях в час.
Обычно
кроме крепления устройства к перекладине требуется подобрать размер
колеса велосипеда. Этот размер обычно указывается на самой шине в некоторых
некое стандартизированное обозначение. Это обозначение, очевидно, имеет огромное значение.
к цифровому измерителю, так как он будет использоваться для расчета расстояния, на котором
крышки с одним оборотом колеса. Датчик на перекладине определяет каждый полный оборот
и отправьте на счетчик, который дополнительно отслеживает время. Зная расстояние, которое
было пройдено, и время, которое потребовалось, счетчик вычисляет скорость, используя простой
уравнение: скорость = расстояние/время. Если мы возьмем расстояние в милях и время в
часов мы получим скорость в милях в час.Интересное наблюдение: если диаметр круга равен 1, его длина окружности это точно значение π, а именно 3,14.
Рассмотрим несколько примеров применения формулы.
 Следующее
два простых упражнения помогут применить теорию на практике и, надеюсь, помогут
чтобы устранить любую неопределенность, которая у вас все еще может быть.
Следующее
два простых упражнения помогут применить теорию на практике и, надеюсь, помогут
чтобы устранить любую неопределенность, которая у вас все еще может быть.Упражнение 1: Вычислите длину окружности с радиусом
4 дюйма .Решение: Используя стандартное уравнение, длина окружности рассчитывается в следующим образом:
окружность = 2 * π * радиус
Заменим переменные значениями:
радиус = 4
π = 3,14 (значение округлено до двух знаков после запятой)
окружность = 2 * 3,14 * 4
окружность = 25,12 дюймаПоэтому, используя обычное уравнение, мы вычислили результат упражнения быть 25,12 дюйма . Очевидно, что результат всегда находится в тех же единицах, что и указан радиус; радиус был указан в дюймах, поэтому результат выражается в дюймах тоже.
 Если радиус был выражен в метрах, результат будет в метрах
и так далее.
Если радиус был выражен в метрах, результат будет в метрах
и так далее.Упражнение 2: длина окружности равна
10 м . Как долго диаметр этого круга?Решение: Для решения этого упражнения необходимо перевернуть уравнение, так как Окружность — это известный фактор, а диаметр — неизвестный, который нам нужно найти. Как уже было сказано, диаметр в два раза больше длины, чем радиус. Следовательно мы будем использовать следующие два уравнения для решения упражнения:
окружность = 2 * π * радиус
диаметр = 2 * радиусМы видим, что оба уравнения содержат 2 * радиус. Поэтому, используя тот факт, что 2 * радиус равен диаметру из второго уравнения, мы можем заменить эту часть в первом уравнении получить:
окружность = π * диаметр
Поскольку это диаметр, который мы ищем, нам нужно преобразовать уравнение до:
диаметр = окружность ÷ π
Заменим переменную известными значениями:
диаметр = 10 ÷ 3,14
диаметр = 3,18 м (приблизительно до 2 знаков после запятой)Преобразовав исходное уравнение, мы вычислили, что диаметр окружности с окружностью 10 метров составляет 3,18 метра .

Окружность
Окружность — это тип фигуры в геометрии, в которой расстояние от края окружности до центра одинаково в любой точке.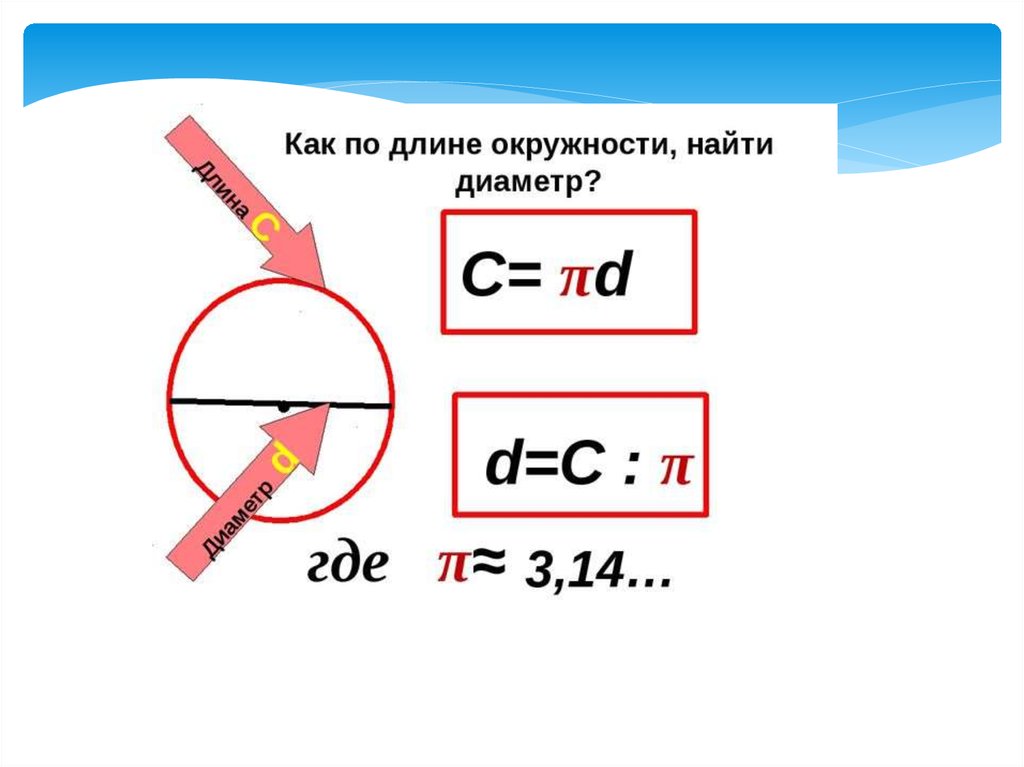
Центр
Это в основном центр круга.
Окружность
Мы уже узнали, что периметр означает расстояние или длину окружающего пространства, и мы уже вычислили периметр квадрата . В случае круга обычно используется термин окружность.
Радиус
Радиус — это расстояние от края круга до центра. Обозначается как ‘ r’ .
Диаметр
Диаметр — это длина любой прямой линии в окружности, проходящей через центр.
Полукруг
Полукруг означает половину круга. Если диаметр делит круг на две половины, то каждая часть будет называться полукругом.
Значение Пи
Окружность круга
Периметр двухмерных фигур определяется как длина их внешней периферии. Можно использовать полигоны любой формы; они не обязательно должны быть правильными геометрическими фигурами. Вы задаетесь вопросом, как рассчитать, сколько ограждений вам понадобится, чтобы оградить участок, если вы хотите его оградить. Вы можете рассчитать необходимое количество ограждений, просто посчитав периметр участка. Окружность круга также называют периметром круга.
Окружность круга в основном означает периметр круга. Это та же философия, что и у квадратов или прямоугольников. Теперь в случае с кругом нет прямой линии.
Здесь на сцену выходит термин окружность . Это просто расстояние по кругу или общая длина по кругу.
Формула длины окружности
В предыдущем уроке мы поняли, что периметр подразумевает общую длину ребра. Давайте узнаем формулу длины окружности!
Допустим,
SO,
C = πd
Периметр или окружно x 2r = 2πr
Длина окружности формулаДлина окружности = 2π x Радиус окружности
Это уравнение для длины окружности.
Теперь формула длины окружности применима тремя способами:
Если известен радиус (r)
Мы можем рассчитать длину окружности, если радиус известна,
Окружность или периметр (C) = 2 π r
Если диаметр (D) известен
Мы можем вычислить длину окружности, если известен диаметр,
Окружность или периметр (C) = πD
Если площадь известна
The area of a circle,
A = πD 2 /4
or, D 2 = 4A/π
or, D = √(4A/π)
Circumference,
C = πD
или C = πD = π √(4A/π) = √(4πA)
Это длина окружности по формуле.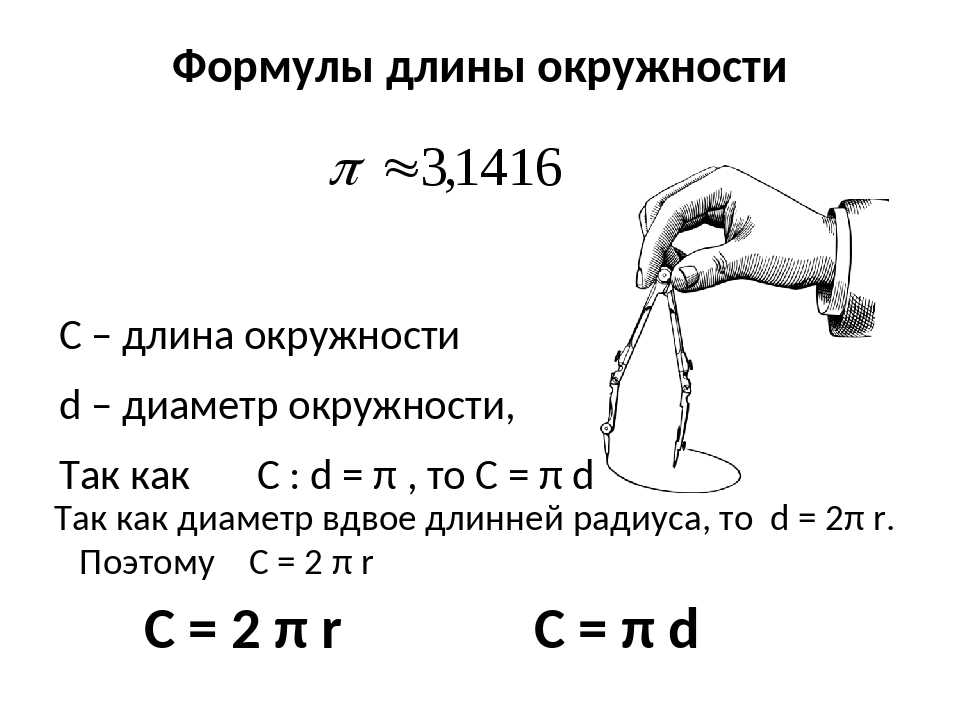
Периметр полукруга
Мы уже узнали периметр круга.
С = 2πr.
Теперь полукруг означает половину круга.
Итак, периметр круга = 2πr / 2 = πr
Как найти периметр круга радиусом 50м?
Попробуем понять понятие периметра круга на простом примере шаг за шагом.
Радиус окружности 50м. Теперь, каков периметр круга?
Шаг-1: Данными данными является радиус окружности, r = 50м.
Шаг-2: Диаметр круга, D = 2r = 2 x 50м = 100м.
Шаг 3: Периметр или окружность, C = πD = 3,14 x 100 м = 314 м.
Шаг 4: Его можно рассчитать напрямую, используя формулу длины окружности, C = 2πr = 2 x 3,14 x 50 = 314 м
Проверьте онлайн-калькулятор для длины окружности .
Вывод длины окружности
Длина окружности не является правильной фигурой, поэтому для расчетов нельзя использовать линейку. Вот шаги для расчета окружности:
Вы можете проследить путь круглого плоского объекта с помощью какой-нибудь нити.
С помощью линейки измерьте длину нити, необходимой для обведения всей границы круглой плоскости. Эта длина и будет окружностью круга.
Другой способ определить окружность состоит в том, что длина веревки, которая точно окружает ее границу, будет равна ее окружности.
Геометрический расчет окружности
Радиус круглой плоскости можно измерить линейкой или рулеткой.
Вы можете вычислить измеренное значение радиуса, используя приведенную ниже формулу
Формула для длины окружности:
C = 2πR = πD
где, C = длина окружности и π = постоянная произносится как «пи ” со значением 22/7 или 3,14.
Примеры длины окружности
Давайте разработаем несколько примеров того, как узнать периметр окружности!
Пример-1
Возьмите круглый диск. Радиус круглого диска равен 5 м. Узнайте длину окружности.
Решение
Радиус кругового диска = 5 м.
Следовательно, длина окружности круга
C = 2πr
⇒ C = 2 x 3,14 x 5 м
⇒ C = 31,4 м
Следовательно, длина окружности диска равна 31,4 м.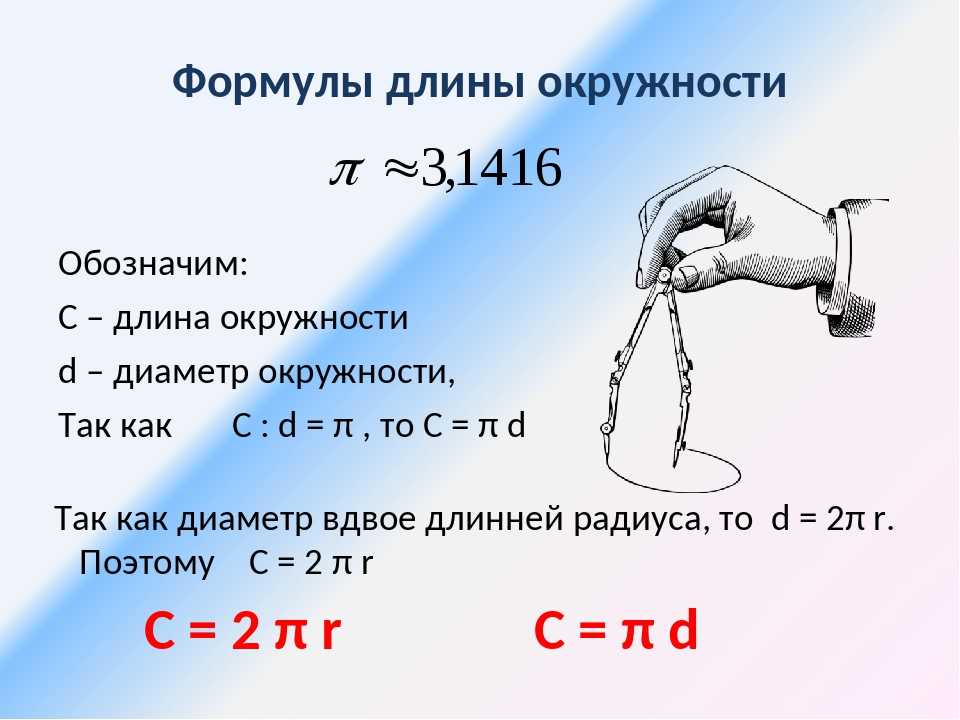
Пример-2
Колесо автомобиля Toyota имеет диаметр 18 дюймов. Найдите расстояние, пройденное колесом за один оборот.
Решение
Диаметр колеса автомобиля Toyota = D = 18
Периметр колеса = πD = 3,14 x 18 = 56,52 дюйма.
Следовательно, периметр или длина окружности колеса равна 56,52 м.
Пример-3
Найдите длину окружности идеального круга радиусом 8 см.
Решение
Радиус идеального круга = 8см.
Следовательно, длина окружности идеального круга
C = 2πr
⇒ C = 2 x 3,14 x 8 см
⇒ C = 50,24 см
Следовательно, периметр круга равен 50,24см.
Пример-4
Найдите диаметр круга, длина окружности которого равна 66 м. [Возьмем π = 22/7]
Решение
Данные, длина окружности, C = 49 м,
Согласно уравнению, мы знаем, ⇒ D = 66 х 7 / 22
⇒ D = 21м.
Периметр круга равен 21 м.
Пример-5
Периметр полукруглой шкалы равен 88 см, найдите радиус шкалы. [Возьмем π = 22/7]
Решение
Даны данные, периметр полукруга,
c = C/2 = 88 см,
⇒ C = 88×2
Согласно уравнению, мы можем написать ,
C = 2πr
⇒ 88 х 2 = 2 х 22/7 х r
⇒ r = 88 х 2 х (7/22) / 2
⇒ r = 28 м.
Периметр полукруга равен 28м.
Пример-6
Окружность круглой пластины превышает радиус на 22,7 см. Найдите диаметр круга. [Считайте π = 22/7]
Решение
Поскольку радиус не указан, считайте, что радиус круглой пластины равен r см.
Итак, исходя из определения диаметра,
Мы можем написать,
Диаметр, D = 2r
Окружность. C = πD = 2πr см
Теперь по условию
Круговая пластина превышает радиус на 22,7 см
Итак, длина окружности = радиус + 22,7
⇒ 2πr = r + 22,7
⇒ 2 × (22/7) × r = r + 22,7
⇒ 44r = 7r + 22,7 × 7
⇒ 44r – 7r ⇒ 9037 ⇒ 901,9 r = 158,9
⇒ r = 158,9 / 37
⇒ r = 4,29
Следовательно, радиус круглой пластины равен 4,29 см.
И диаметр, D = 2r = 2 x 4,29 = 8,59см.
Пример-7
Найдите длину окружности Земли. [Диаметр Земли 2742 км]
Решение
Диаметр Земли, D = 12742км.
Следовательно, длина окружности Земли
C = πD
⇒ C = 3,14 x 12742
⇒ C = 40009,88 км
Следовательно, длина окружности Земли равна 80009,8.
Ключевые математические вычисления Решение длины окружности
Рассчитайте расстояние, пройденное транспортным средством с колесами 24 см за один полный оборот?
Расстояние, пройденное колесом за один полный оборот = длина окружности колеса = периметр окружности = 2πR
Здесь, R=24 см
Пройденное расстояние = 2x (22/7) x24
= 66×3 = 198 см
Как найти окружность площади?
Если вы хотите вычислить площадь круга с радиусом, вы должны сначала возвести радиус в квадрат или умножить его на себя. Тогда площадь будет равна пи, умноженному на квадрат радиуса. Кроме того, найдите площадь с диаметром, просто разделив диаметр на 2, а затем примените формулу радиуса.
Кроме того, найдите площадь с диаметром, просто разделив диаметр на 2, а затем примените формулу радиуса.
Какова формула длины окружности полукруга?
Периметр круга равен 2πR, где R — радиус круга. Другими словами, длина окружности равна половине длины окружности, равной πR.
Какова формула длины окружности?
Длина окружности измеряется пропорционально ее диаметру и радиусу. Окружность рассчитывается путем умножения значения числа пи на радиус этой окружности. Длина окружности равна диаметру окружности, умноженному на число пи (22/7 или 3,14) в квадрате.
Какова длина окружности, радиус которой равен 49?
Если мы хотим определить длину окружности по заданному радиусу, сначала нужно знать уравнение окружности = 2πR.
Затем мы подставляем число радиуса в уравнение, которое дает
Окружность = 2 * 49 * π
Мы умножаем, чтобы найти значение окружности: 2 * 49 * 22/7
Ответ: 288.
Решенные задачи на периметр круга
Найдите радиус круга с длиной окружности 220 дюймов, используя формулу периметра круга?
Вы должны найти радиус окружности, если длина окружности равна 220 дюймов, на основе формулы периметра окружности.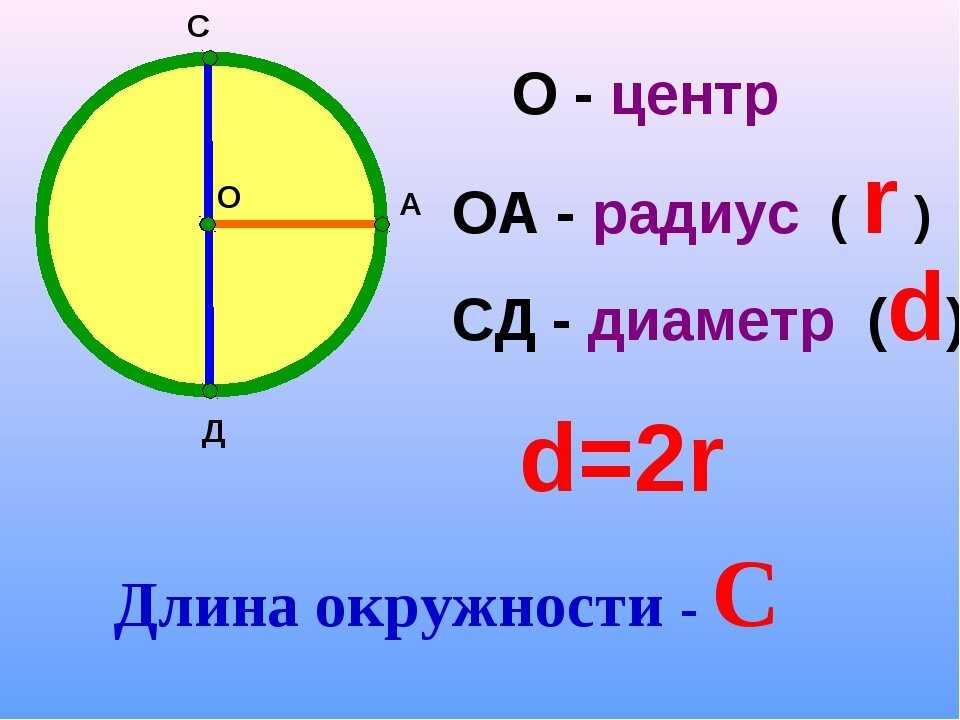
Периметр или окружность круга равняется 2πr
2 π r = 220
2 × 22/7 × r = 220
R = 220 × 7/44
R = 35 см
. круга = 35 см.
Найдите площадь и периметр круглой фигуры диаметром 28 см?
Диаметр = 28 см
Следовательно, радиус = 28/2 = 14 см
Область = 𝜋R2
Область = 22/7 x 14 x 14
Область = 616 см кв. Периметр = 88 см
Метод: Два
Периметр = 𝜋D
Периметр = 22/7 x 28
Периметр = 88 см
см = Площадь = 616 см кв. Круг разделен на две части по диаметру так, чтобы их площади были равны. Это называется полукругом. Площадь полукруга будет в два раза меньше круга, так как он в два раза меньше круга. Полуокружности образуются, когда дуга окружности делит диаметр на две равные половины. Это наиболее распространенная форма в реальной жизни, например транспортир, спидометр, тако и т. Триггерная окружность также известна как единичная окружность. В единичной окружности можно вычислить тангенс, синус и косинус любого угла в диапазоне от 0 до 360 градусов. Длину дуги можно определить, разделив угол центральной точки дуги на 360 градусов. Затем число необходимо умножить на радиус окружности. Длину дуги можно определить, умножив это число на 2 * π. Полукруг можно рассматривать как имеющий вписанный в него угол. Кроме того, приводятся доказательства того, что угол, заключенный в полуокружность, пересекает дугу в 180 градусов. Следовательно, угол, который необходимо измерить, должен составлять половину от 180 градусов, что составляет 90 градусов. Прямой угол также называют углом, если угол равен 90 градусов. Найдите длину окружности Диаметр окружности 4,2 дюйма Чтобы найти периметр окружности, Периметр окружности равен π D Окружность или периметр = 22/7 × 4,2 = 13,2 дюйма Ответ: Длина окружности = 13,2 дюйма. При заданной длине периметра наибольшую площадь имеет круг. Его форма очень симметрична в том смысле, что каждая линия, проходящая через его центр, образует симметрию отражения. Кроме того, он обладает вращательной симметрией вокруг себя со всех сторон. Заштрихованная область = π (40²) – π (30²) = 1600 – 900 × 22/7 = 700 × 22/7 = 2200 кв.см Определение полукруга
 д.
д. Важность единичной окружности
Можете ли вы найти длину дуги?
Можете ли вы вписать прямой угол в полуокружность?
Формула периметра круга используется для расчета длины окружности диаметром 4,2 дюйма.
 Вы можете присвоить значение π как 22/7, используя приведенную формулу?
Вы можете присвоить значение π как 22/7, используя приведенную формулу? Почему круг так важен в геометрии?
Свойства окружности
Какова площадь кольцеобразной области, заключенной между двумя концентрическими окружностями радиусами 40 см и 30 см?

 Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.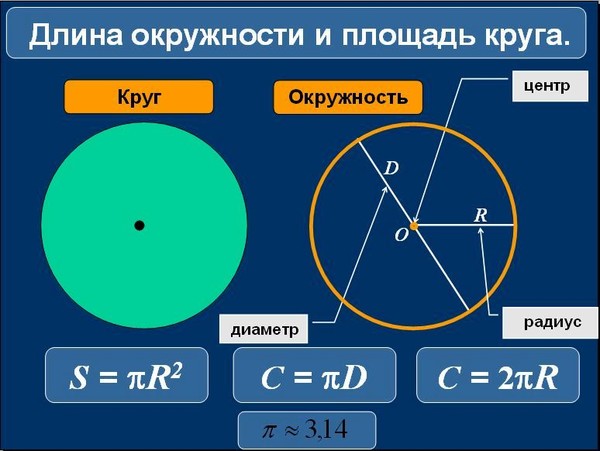 . или приблизительно 3,14.
. или приблизительно 3,14.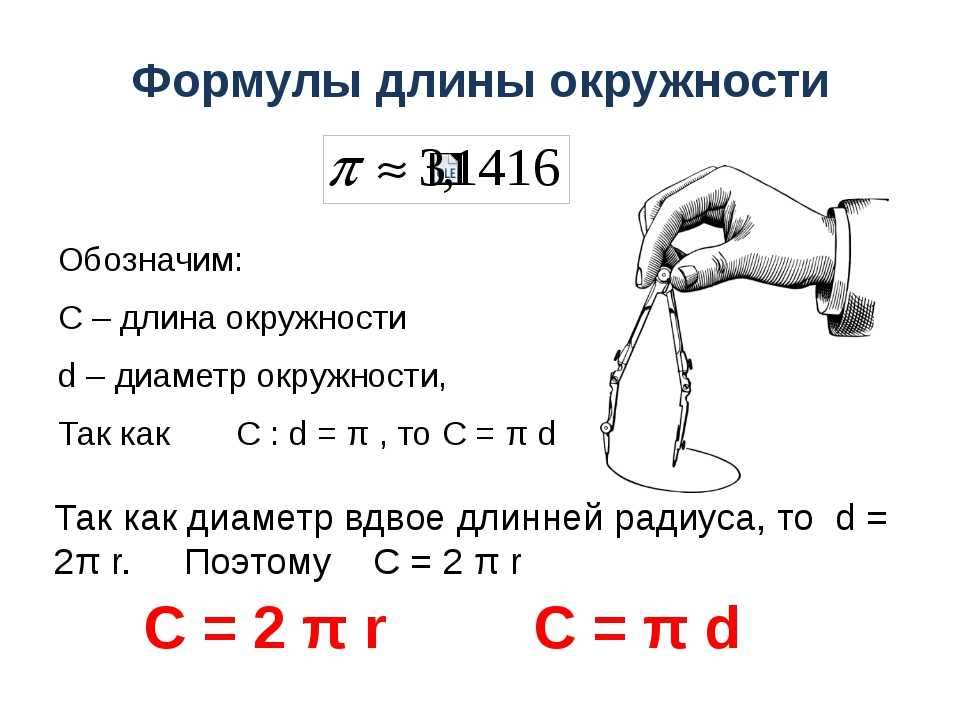

 футов
футов
 Окружность круга — это расстояние вокруг его внешней стороны.
Окружность круга — это расстояние вокруг его внешней стороны. Окружность = 𝜋 диаметр, или окружность = 2 𝜋 радиус, если эта константа равна числу 𝜋.
Окружность = 𝜋 диаметр, или окружность = 2 𝜋 радиус, если эта константа равна числу 𝜋.

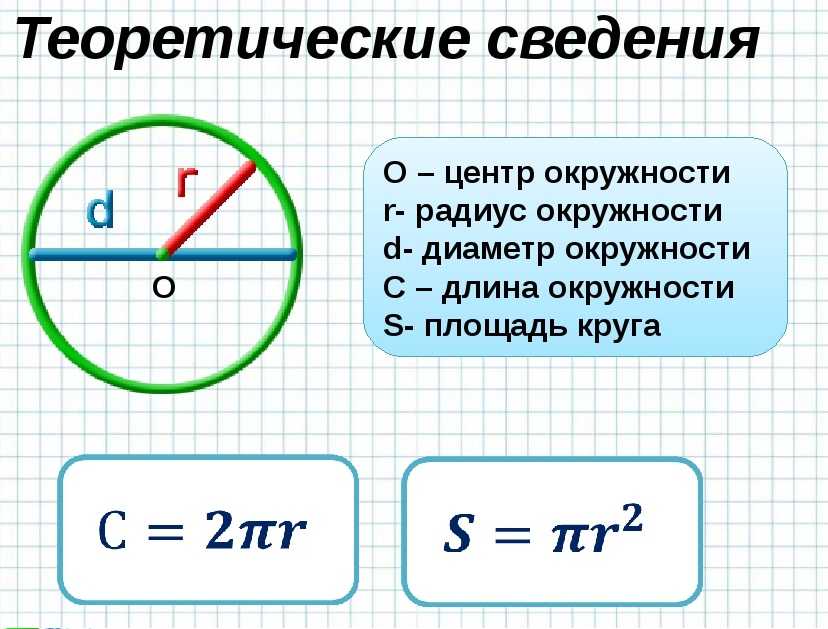 Популярное уравнение требует, чтобы диаметр был известен,
что, в свою очередь, всегда удваивает радиус. Поэтому расчет всегда
уравнение с одним неизвестным:
Популярное уравнение требует, чтобы диаметр был известен,
что, в свою очередь, всегда удваивает радиус. Поэтому расчет всегда
уравнение с одним неизвестным: Делаем еще одну отметку в
то место на полу. Теперь мы можем просто вычислить расстояние между двумя
отметки на полу с помощью простой рулетки. Это расстояние будет равно
окружность данного кольца. Прокатывая кольцо, мы должны убедиться, что кольцо
не скользит, так как это может исказить результат измерения.
Делаем еще одну отметку в
то место на полу. Теперь мы можем просто вычислить расстояние между двумя
отметки на полу с помощью простой рулетки. Это расстояние будет равно
окружность данного кольца. Прокатывая кольцо, мы должны убедиться, что кольцо
не скользит, так как это может исказить результат измерения.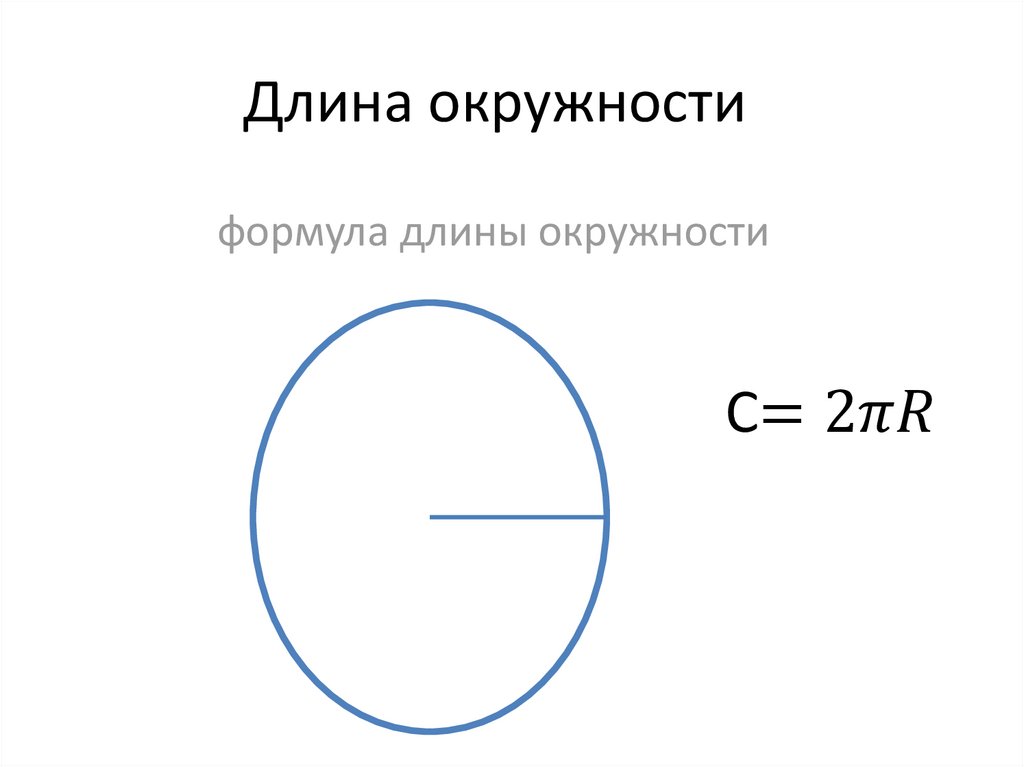 Обычно
кроме крепления устройства к перекладине требуется подобрать размер
колеса велосипеда. Этот размер обычно указывается на самой шине в некоторых
некое стандартизированное обозначение. Это обозначение, очевидно, имеет огромное значение.
к цифровому измерителю, так как он будет использоваться для расчета расстояния, на котором
крышки с одним оборотом колеса. Датчик на перекладине определяет каждый полный оборот
и отправьте на счетчик, который дополнительно отслеживает время. Зная расстояние, которое
было пройдено, и время, которое потребовалось, счетчик вычисляет скорость, используя простой
уравнение: скорость = расстояние/время. Если мы возьмем расстояние в милях и время в
часов мы получим скорость в милях в час.
Обычно
кроме крепления устройства к перекладине требуется подобрать размер
колеса велосипеда. Этот размер обычно указывается на самой шине в некоторых
некое стандартизированное обозначение. Это обозначение, очевидно, имеет огромное значение.
к цифровому измерителю, так как он будет использоваться для расчета расстояния, на котором
крышки с одним оборотом колеса. Датчик на перекладине определяет каждый полный оборот
и отправьте на счетчик, который дополнительно отслеживает время. Зная расстояние, которое
было пройдено, и время, которое потребовалось, счетчик вычисляет скорость, используя простой
уравнение: скорость = расстояние/время. Если мы возьмем расстояние в милях и время в
часов мы получим скорость в милях в час. Следующее
два простых упражнения помогут применить теорию на практике и, надеюсь, помогут
чтобы устранить любую неопределенность, которая у вас все еще может быть.
Следующее
два простых упражнения помогут применить теорию на практике и, надеюсь, помогут
чтобы устранить любую неопределенность, которая у вас все еще может быть. Если радиус был выражен в метрах, результат будет в метрах
и так далее.
Если радиус был выражен в метрах, результат будет в метрах
и так далее.