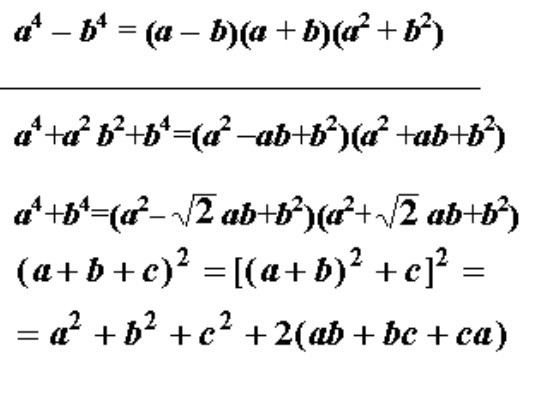Формула разности четвертой степени: Разность четвертой степени | Формулы с примерами

формула разности квадратов, примеры задач

Основные понятия

Существуют формулы, сокращающие процесс умножения. Такие закономерности часто используют на уроках алгебры и при решении самостоятельных работ в средних классах школы. Любая формула сокращенного умножения — это тождество. Таким образом, подобные формулы справедливы в обоих направлениях, то есть допускается переход слева направо и справа налево. 

Рассмотрим такое тождество:

(a-b)(a+b)=a2-b2

Если изменить в этом тождестве расположение правой и левой частей, то получим:

a2-b2=(a-b)(a+b)

Данное тождество называют формулой разности квадратов.

Определение 

Разность квадратов двух выражений является произведением разности данных выражений и их суммы.

С помощью формулы разности квадратов удобно разложить на множители разность квадратов любой пары выражений. Предположим, что имеется некий двучлен, который требуется разложить на множители:

49×2–16y6

Выполнить такое преобразование просто. Достаточно записать многочлен, как разность, с помощью формулы разности квадратов:

49×2–16y6=(7x)2–(4y3)2=(7x–4y3)(7x+4y3)

Алгоритм разложения разности квадратов

В процессе решения практических примеров полезно руководствоваться алгоритмом разложения разности квадратов:

1. Преобразовать выражение, чтобы получились квадраты. При этом нужно использовать свойства степени.
2. Разложить разность квадратов на множители.
3. Найти корни, записать ответ.

Воспользуемся описанной выше последовательностью действий, чтобы преобразовать такое выражение:

25y2-16z10

Запишем каждое из выражений, как квадрат, применив свойство степени:

25y2-16z10=(5y)2-(4z5)2

Далее получится разложить разность квадратов на множители:

(5y-4z5)(5y+4z5)

Схематично действие разложения разности квадратов на множители выглядит следующим образом:

Разберем еще одну задачу с объяснением действий. Предположим, что имеется некий двучлен, который нужно записать в виде разности квадратов:

16a2-49b2

Преобразуем каждое выражение, чтобы получить квадраты по схеме:

Источник: www.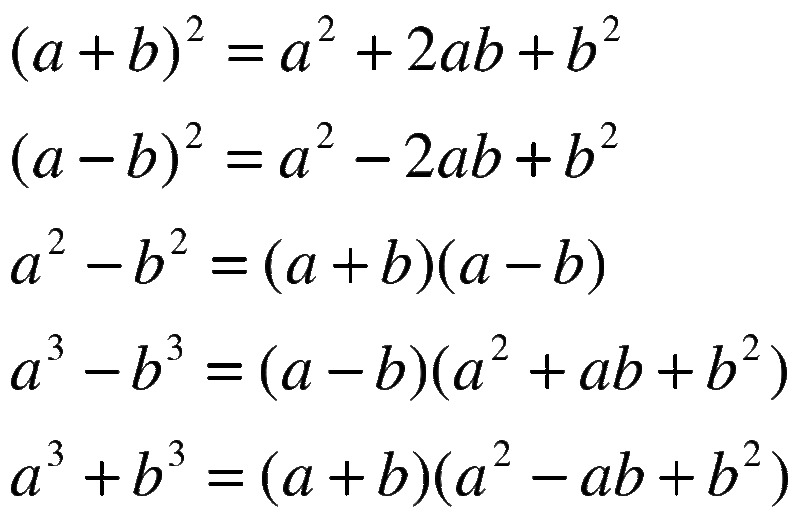 algebraclass.ru

Рассмотрим еще несколько примеров:

0,81m2-0,0036n2=(0,9m)2-(0,06n)2=(0,9m-0,06n)(0,9m+0,06n)

2564×6-49y2=(58×3)2-(23y)2=(58×3-23y)(58×3+23y)

549t2-1=499t2-12=(73t-1)(73t+1)=(213t-1)(213t+1)

В последнем выражении для записи смешанного числа как квадрата мы привели его в вид неправильной дроби. После разложения разности квадратов на множители неправильная дробь была представлена в виде смешанного числа. Для этого потребовалось выделить целую часть.

Примеры заданий с пояснениями

Закрепить тему поможет решение нескольких типичных задач. Например, разложим на множители разность квадратов:

64y2–36×2

Заметим, что:

64y2=(8y)2

36×2=(6x)2

Используя формулу разности квадратов, преобразуем выражение:

Выполним обратное действие, то есть запишем произведение многочленов, как разность квадратов с помощью формулы сокращенного умножения:

(c + 3d)(c – 3d)

Заметим, что произведение многочленов является правой частью формулы разности квадратов. Используем эту формулу в обратном порядке:

Предположим, что требуется упростить произведение многочленов:

(x2+4y3)(x2-4y3)

Заметим сходство выражения с правой частью формулы разности квадратов.

Примечание 1

Одночлены, которые составляют формулу разности квадратов, могут быть возведены в степень.

Выполним преобразования с помощью формулы разности квадратов:

При решении задач можно встретить более сложные задания. К примеру, попробуем разложить на множители такой многочлен:

(a+2b)2–9a2

Запишем выражение в виде разности квадратов:

Примечание 2

В формуле разности квадратов допускается наличие одночленов, которые заключены в скобки, то есть являются многочленами.

Выполним преобразования, согласно стандартному алгоритму, а в конце приведем подобные:

Источник: math-prosto.ru

Задания для самостоятельного решения

Задача 1

Требуется разложить на множители следующие многочлены, используя формулу квадрата разности:

х2-у2 

с2-z2

а2-25

m2-1

16-b2

100-х2

р2-400

у2-0,09

1,44-а2

b2-49

916-n2

2549-p2

Решение

х2-у2=(х-у)(х+у) 

с2-z2=(c-z)(c+z)

а2-25=(а-5)(а+5)

m2-1=(m-1)(m+1)

16-b2=(4-b)(4+b)

100-х2=(10-х)(10+х)

р2-400=(р-20)(р+20)

у2-0,09=(y-0,3)(y+0,3)

1,44-а2=(1,2-а)(1,2+а)

b2-49=(b-23)(b+23)

916-n2=(34-n)(34+n)

2549-p2=(57-р)(57+р)

Задача 2

Выполнить разложение на множители следующих выражений:

25×2-у2   

-m2+16n2

36а2-49

64-25×2

9m2-16n2

64р2-81q2

-49а2+16b2

0,01n2-4m2

9-b2с2

4а2b2-1

р2-а2b2

16c2d2-9а2

Решение

25×2-у2=(5x-y)(5x+y)    

-m2+16n2=(4n-m)(4n+m)

36а2-49=(6a-7)(6a+7)

64-25×2=(8-5x)(8-5x)

9m2-16n2=(3m-4n)(3m+4n)

64р2-81q2=(8p-9q)(8p+9q)

-49а2+16b2=(4b-7a)(4b+7a)

0,01n2-4m2=(0,1n-2m)(0,1n+2m)

9-b2с2=(3-bc)(3+bc)

4а2b2-1=(2ab-1)(2ab+1)

р2-а2b2=(p-ab)(p+ab)

16c2d2-9а2=(4cd-3a)(4cd+3a)

Задача 3

Найти корни уравнений:

х2-16=0

у2-81=0

19-х2=0

а2-0,25=0

b2+36=0

x2-1=0

4×2-9=0

25×2-16=0

81×2+4=0

Решение

х2-16=0⇒(x-4)(x+4)=0⇒—x=4 или x = -4;

у2-81=0⇒(y-9)(y+9)=0⇒—у=9 или y = -9;

19-х2=0⇒(13-х)(13+x)=0⇒—x=13 или x=-13;

а2-0,25=0⇒(a-0,5)(а+0,5)-0⇒—а=0,5 или а = -0,5;

b2+36=0⇒b2=-36 — решения отсутствуют;

x2-1=0⇒(х-1)(х+1)=0⇒—х=1 или х = -1;

4×2-9=0⇒(2х-3)(2х+3)=0⇒—х=1,5 или х = -1,5;

25×2-16=0⇒(5х-4)(5х+4)=0⇒—х=0,8 или х = -0,8;

81×2+4=0⇒x2=-814 — решения отсутствуют.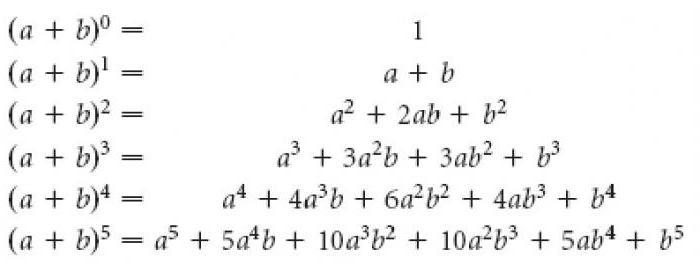 2

Формула четвертой степени

Это известная математическая теорема о том, что существует формула, которая может решать общие уравнения четвертой степени. Формула состоит из сложения, вычитания, умножения, деления и извлечения

n -го корня. Кроме того, такой формулы не существует для общих уравнений пятой степени (или большей степени).

Из-за сложности формулы четвертого числа она почти никогда полностью не выписывается полностью, как более простая квадратная формула. Я полагал, что попытка распечатать его с использованием обычного размера шрифта и отформатировать его как обычное уравнение потребует листа бумаги размером с плакат. Поэтому я решил поместить это на постер!

Я смог найти другие веб-страницы, на которых квадратичная формула была написана полностью, но обнаружил, что они имеют некоторые недостатки. Самое главное, они не всегда работают; есть допустимые входные данные, которые приводят к делению на 0. Кроме того, они используют четыре отдельных уравнения вместо одного и имеют не очень эстетичный формат, по крайней мере, для меня.

Моя цель состояла в том, чтобы написать единую формулу, которая работала бы для всех входных данных. Но я также хотел сделать его как можно более простым и автономным — я не хотел добавлять пункт вроде «выбрать значения для радикалов, которые удовлетворяют такому-то уравнению». Короче говоря, я хотел оформить формулу четвертого числа так, как это обычно делается с формулой квадратного числа. В идеале четыре решения должны быть указаны двумя знаками ±, подобно тому, как квадратичная формула использует один знак ± для указания двух решений.

Было постоянное противоречие между точностью и лаконичностью, но я доволен тем, что получилось. Результатом является единая формула, которая дает все корни всех уравнений четвертой степени с простым правилом выбора радикальных значений и знаков ±. Самая уродливая часть — это длинное выражение (составляющее примерно одну шестую часть формулы), использующее функцию sgn только для того, чтобы получить правильный знак последнего радикала.

Если вы просто хотите посмотреть формулу, я разместил ее в Интернете вместе с формулами для решения многочленов меньшей степени.

Я также делаю его доступным в виде постера в формате PDF (с доступным исходным кодом), базовой веб-страницы, веб-страницы MathJax (загрузка которой может занять несколько минут), веб-страницы MathML (которая поддерживается не во всех браузерах) и текст ASCII. Я также включил математический вывод формулы на случай, если вас интересуют внутренние подробности. И поскольку формула четвертого числа опирается на кубическую и квадратичную формулы, я также делаю вышеприведенное доступным и для этих формул. Интересно посмотреть, как та же самая общая методология, которая решает квартику, может также использоваться для решения кубических и квадратичных чисел.

Для верстки плаката я использовал TeX (конечно) и размер бумаги в половину A0. Хотя шрифты Computer Modern могут быть сгенерированы любого необходимого размера, версии Type 1 доступны только в фиксированном количестве размеров, поэтому мне пришлось сделать некоторые замены и масштабировать шрифты по мере необходимости. В PDF-файлах типа 3 используются шрифты точно правильного размера, но они не содержат подсказок и будут плохо выглядеть на экране, но они могут быть полезны, если вы решите распечатать плакат.

Загрузки

• Квартальная формула
  • Постер в формате PDF
  • Постер в формате PDF, тип 3
  • Веб-страница
  • Веб-страница MathJax
  • Веб-страница MathML
  • ASCII-код
  • Математический вывод
• Кубическая формула
  • Бумага PDF A4
  • Тип 3 PDF Бумага A4
  • Веб-страница
  • Веб-страница MathJax
  • Веб-страница MathML
  • ASCII-код
  • Математический вывод
• Квадратичная формула
  • Бумага PDF A4
  • Тип 3 PDF Бумага A4
  • Веб-страница
  • Веб-страница MathJax
  • Веб-страница MathML
  • ASCII-код
  • Математический вывод
• Линейная формула
  • Бумага PDF A4
  • Тип 3 PDF Бумага A4
  • Веб-страница
  • Веб-страница MathJax
  • Веб-страница MathML
  • ASCII-код
  • Математический вывод
• Все формулы
  • Плакат в формате PDF A0
  • Тип 3 PDF A0 Плакат
  • Веб-страница
  • Веб-страница MathJax
  • Веб-страница MathML
  • ASCII-код

Альтернативные форматы

Формат PDF:

Тип 1 Тип 3

Формат веб-страницы:

PNGMathJaxMathML

Источник постера

• Репозиторий GitHub26

Факторинг квартик

Факторинг квартик

		Трудности и запросы
	Имя: Кайл Уровень: Среднее (Алг. 2) Кто?: Учитель Как мне разложить у 4 + у 2 +1?? Я думаю, что ответ (y 2 + y + 1)(y 2 — y + 1), но я не уверен, как это получить… Кайл
	Кайл, В конце решения ежемесячной задачи Math Central, MP41, обсуждается факторизация квартик (апрель 2004 г.). Ниже приведена копия этого обсуждения. Вопрос: Как разложить на множители многочлен четвертой степени ? Общая квартика выглядит как р(х) = с 4 х 4 + с 3 х 3 + к 2 х 2 + к 1 х + к 0 , или в его однородной форме (заменив x на a / b и умножив на b 4 ), q(a, b) = c 4 a 4 + c 3 a 3 b + c 2 a 2 b 2 + c 1 ab 3 + c 0 б 4 . Это факт, что любой многочлен четвертой степени с действительными коэффициентами можно разложить на множители в виде произведения двух квадратных многочленов с действительными коэффициентами. Эта формула известна с шестнадцатого века, и легко доступно программное обеспечение, которое выполняет факторизацию за вас; см., например, http://mathworld.wolfram.com/QuarticEquation.html С другой стороны, факторизация практична только в особых случаях, таких как q(a, b) = a 4 + b 4 . Здесь нет необходимости запоминать формулы. По симметрии факторизация должна выглядеть как . а 4 + б 4 = (а 2 + хаб + б 2 )(а 2 + яб + б 2 ). Чтобы найти x и y, разверните правую часть и заметьте, что коэффициенты a 3 b и ab 3 равны x + y, а коэффициенты a 2 b 2 равны 2 + xy. Чтобы выполнялось равенство, оба эти коэффициента должны быть равны нулю, поэтому x = –y = √2. Таким образом, а 4 + б 4 = (а 2 + √2 аб + b 2 )(а 2 – √2 аб + b 2 ). Чтобы разложить a 4 + 4c 4 (= a 4 + (√2 c) 4 ), можно использовать b = √2 c в нашей формуле; в качестве альтернативы решите a 4 + 4c 4 = (a 2 + xac + 2c 2 )(a 2 – xac + 2c 2 ) относительно x. В любом случае получается формула, используемая в нашем первом решении. Борнштейн присоединил к этой формуле имя Софи Жермен (1776–1831), но было бы удивительно, если бы древние греки не знали его за 2000 лет до рождения Жермен. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт