как вывести забытую тригонометрическую формулу?
На олимпиаде по математике с большой степенью вероятности, а на внешнем независимом тестировании – уж наверняка встретятся задания по тригонометрии. Тригонометрию часто не любят за необходимость зубрить огромное количество трудных формул, кишащих синусами, косинусами, тангенсами и котангенсами. На сайте уже когда-то давались советы, как вспомнить забытую формулу, на примере формул Эйлера и Пиля.
А в этой статье мы постараемся показать, что достаточно твёрдо знать всего пять простейших тригонометрических формул, а об остальных иметь общее представление и выводить их по ходу дела. Это как с ДНК: в молекуле не хранятся полные чертежи готового живого существа. Там содержатся, скорее, инструкции по его сборке из имеющихся аминокислот. Так и в тригонометрии, зная некоторые общие принципы, мы получим все необходимые формулы из небольшого набора тех, которые нужно обязательно держать в голове.
Будем опираться на следующие формулы:
- Основное тригонометрическое тождество: sin2a+cos2a = 1
- Определение тангенса:
- Определение котангенса:
- Формула синуса суммы: sin(a+b) = sinacosb+cosasinb
- Формула косинуса суммы: cos(a+b) = cosacosb—sinasinb
Из формул синуса и косинуса сумм, зная о чётности функции косинуса и о нечётности функции синуса, подставив -b вместо b, получаем формулы для разностей:
- Синус разности: sin(a-b) = sinacos(-b)+cosasin(-b) = sinacosb—cosasinb
- Косинус разности: cos(a-b) = cosacos(-b)—sinasin(-b) = cosacosb+sinasinb
Поставляя в эти же формулы a = b, получаем формулы синуса и косинуса двойных углов:
- Синус двойного угла: sin2a = sin(a+a) = sinacosa+
- Косинус двойного угла: cos2a = cos(a+a) = cosacosa—sinasina = cos2a—sin2a
Аналогично получаются и формулы других кратных углов:
- Синус тройного угла: sin3a = sin(2a+a) = sin2acosa+cos2asina = (2sinacosa)cosa+(cos2a—sin2a)sin a = 2sinacos2a+sinacos2a—sin3a = 3sinacos2a—sin3a = 3sina(1-sin2a)-sin3a = 3sina-4sin3a
- Косинус тройного угла: cos3a = cos(2a+a) = cos2acosa—sin2asina = (cos2a—sin2a)cosa-(2sinacosa)sina = cos3a-
Прежде чем двигаться дальше, рассмотрим одну задачу.
Дано: угол — острый.
Найти его косинус, если
Решение, данное одним учеником:
Т.к. , то sina = 3,а cosa = 4.
(Из математического юмора)
Итак, определение тангенса связывает эту функцию и с синусом, и с косинусом. Но можно получить формулу, дающую связь тангенса только с косинусом. Для её вывода возьмём основное тригонометрическое тождество: sin
2a+cos2a = 1 и разделим его на cos2a. Получим:- Связь тангенса и косинуса:
Так что решением этой задачи будет:
(Т.к. угол острый, при извлечении корня берётся знак +)
- Аналогично получаем связь котангенса и синуса:
Формула тангенса суммы – ещё одна, тяжело поддающаяся запоминанию. Выведем её так:
- Формула тангенса суммы: . Разделив числитель и знаменатель на произведение косинусов, получим:
Сразу выводится и
- Формула тангенса двойного угла:
Из формулы косинуса двойного угла можно получить формулы синуса и косинуса для половинного. Для этого к левой части формулы косинуса двойного угла:
прибавляем единицу, а к правой – тригонометрическую единицу, т.е. сумму квадратов синуса и косинуса.
cos2a+1 = cos2a—sin2a+cos2a+sin2a
2cos2a = cos2a+1
Выражая cosa через cos2a и выполняя замену переменных, получаем:
- Косинус половинного угла:
Знак берётся в зависимости от квадранта.
Аналогично, отняв от левой части равенства единицу, а от правой — сумму квадратов синуса и косинуса, получим:
2sin2a = 1-cos2a
- Cинус половинного угла:
И, наконец, чтобы преобразовать сумму тригонометрических функций в произведение, используем следующий приём. Допустим, нам нужно представить в виде произведения сумму синусов sina+sinb. Введём переменные x и y такие, что a = x+y, b+x-y. Тогда
sina+sinb = sin(x+y)+sin(x-y) = sinxcosy+cosx
Поскольку a = x+y, b = x-y, то . Поэтому
- Представление суммы синусов в виде произведения:
Сразу же можно вывести
- Формулу для разбиения произведения синуса и косинуса в сумму: sinacosb = 0.5(sin(a+b)+sin(a-b))
Рекомендуем потренироваться и вывести самостоятельно формулы для преобразования в произведение разности синусов и суммы и разности косинусов, а также для разбиения в сумму произведений синусов и косинусов. Проделав эти упражнения, вы досконально освоите мастерство вывода тригонометрических формул и не потеряетесь даже на самой сложной контрольной, олимпиаде или тестировании.
Тригонометрические формулы. Основные тригонометрические тождества. Тригонометрические тождества
Основные тригонометрические тождества
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
- ctg (α — β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- tg 3α = (3tg α — tg³ α) ÷ (1 — 3tg² α)
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Переход от суммы к произведению
Другие заметки по алгебре и геометрии
определение, формула, таблица, график, свойства
Определение
Синус острого угла α (sin α) – это отношение противолежащего катета (a) к гипотенузе (c) в прямоугольном треугольнике.
sin α = a / c

Например:
a = 3
c = 5
sin α = a / c = 3 / 5 = 0.6
График синуса
Функция синуса пишется как y = sin (x). График в общем виде выглядит следующим образом:

Свойства синуса
Ниже в табличном виде представлены основные свойства синуса с формулами:
| Свойство | Формула |
| Симметричность | sin (-α) = -sin α |
| Симметричность | sin (90°- α) = cos α |
| Пифагорейская тригонометрическая идентичность | sin2 α + cos2 α = 1 |
| sin α = cos α tg α | |
| sin α = 1 / csc α | |
| Синус двойного угла | sin 2α = 2 sin α cos α |
| Синус суммы углов | sin (α+β) = sin α cos β + cos α sin β |
| Синус разности углов | sin (α-β) = sin α cos β — cos α sin β |
| Сумма синусов |  |
| Разность синусов |  |
| Произведение синусов |  |
| Произведение синуса и косинуса |  |
| Закон синуса | a / sin α = b / sin β = c / sin γ |
| Производная синуса | sin’ x = cos x |
| Интеграл синуса | ∫ sin x dx = -cos x + C |
| Формула Эйлера | sin x = (eix — e—ix) / 2i |
microexcel.ru
Обратная к синусу функция
Арксинус x – это обратная функция к синусу x, при -1≤x≤1.
Если синус угла у равняется х (sin y = x), значит арксинус x равен у:
arcsin x = sin-1 x = y
Таблица синусов
| x (°) | x (рад) | sin x |
| -90° | -π/2 | -1 |
| -60° | -π/3 | -√3/2 |
| -45° | -π/4 | -√2/2 |
| -30° | -π/6 | -1/2 |
| 0° | 0 | 0 |
| 30° | π/6 | 1/2 |
| 45° | π/4 | √2/2 |
| 60° | π/3 | √3/2 |
| 90° | π/2 | 1 |
microexcel.ru
Основные формулы тригонометрии
- Главная
- Справочник
- Тригонометрия
- Основные формулы тригонометрии
Тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Их всего четыре:
- Синус \( \displaystyle sin\left( x \right) \)
- Косинус \( \displaystyle cos\left( x \right) \)
- Тангенс \( \displaystyle tg\left( x \right) \)
- Котангенс \( \displaystyle ctg\left( x \right) \)
Существует два способа решения тригонометрических уравнений:
Первый способ — с использованием формул.
| \( \displaystyle A \) | \( \displaystyle a \) | \( \displaystyle -1 \) | \( \displaystyle 0 \) | \( \displaystyle 1 \) |
| \( \displaystyle \sin x=A \) | \( \displaystyle {{\left( -1 \right)}^{n}}\arcsin \alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{2}+2\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{2}+2\pi n \) |
| \( \displaystyle \cos x=A \) | \( \displaystyle \pm \arccos \alpha +2\pi n \) | \( \displaystyle \pi +2\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle 2\pi n \) |
| \( \displaystyle tgx=A \) | \( \displaystyle arctg\alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{4}+\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
| \( \displaystyle ctgx=A \) | \( \displaystyle arcctg\alpha +\pi n \) | \( \displaystyle \dfrac{3\pi }{4}+\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
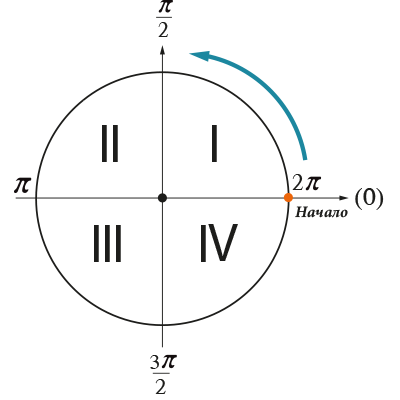
Второй способ — через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.
Основные формулы Тригонометрии:
Основное тригонометрическое тождество (нужно его помнить, даже если тебя разбудили среди ночи и спросили!)
\[ \displaystyle si{{n}^{2}}a+co{{s}^{2}}a=1 \]
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)
\[ \displaystyle tg\ \alpha =\dfrac{sin\ \alpha }{cos\ \alpha } \]
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)
\[ \displaystyle ctg\ \alpha =\dfrac{cos\ \alpha }{sin\ \alpha }=\dfrac{1}{tg\ \alpha } \]
Синус суммы и разности:
\[ \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \]
Косинус суммы и разности:
\[ \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \]
Тангенс суммы и разности:
\[ \displaystyle tg\left( \alpha \pm \beta \right)=\dfrac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta } \]
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.
\[ \displaystyle si{{n}^{2}}\alpha =\dfrac{1-cos2\alpha }{2} \]
\[ \displaystyle co{{s}^{2}}\alpha =\dfrac{1+cos2\alpha }{2} \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
\[ \displaystyle t{{g}^{2}}\alpha =\dfrac{1-cos2\alpha }{1+cos2\alpha },\alpha \ne \dfrac{\pi }{2}+\pi n,n\in Z \]
\[ \displaystyle si{{n}^{3}}\alpha =\dfrac{3sin\alpha -sin3\alpha }{4} \]
\[ \displaystyle co{{s}^{3}}a=\dfrac{3cosa+cos3a}{4} \]
Из данных формул можно в частности вывести формулы тройного угла:
\[ \displaystyle sin3\alpha =3sin\alpha -4si{{n}^{3}}\alpha \]
\[ \displaystyle cos3a=4co{{s}^{3}}a-3cosa \]
\[ \displaystyle tg3\alpha =\dfrac{3tg\alpha -t{{g}^{3}}\alpha }{1-3t{{g}^{2}}\alpha } \]
\[ \displaystyle ctg3\alpha =\dfrac{3ctg\alpha -ct{{g}^{3}}\alpha }{1-3ct{{g}^{2}}\alpha } \]
Формулы преобразования суммы функций
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
\[ \displaystyle sin\alpha \pm sin\beta =2sin\dfrac{\alpha \pm \beta }{2}cos\dfrac{\alpha \mp \beta }{2} \]
\[ \displaystyle cos\alpha +cos\beta =2cos\dfrac{\alpha +\beta }{2}cos\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle cos\alpha -cos\beta =-2sin\dfrac{\alpha +\beta }{2}sin\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle tg\alpha \pm tg\beta =\dfrac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta } \]
\[ \displaystyle ctg\alpha \pm ctg\beta =\dfrac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta } \]
Формулы преобразования произведений функций
\[ \displaystyle sin\alpha sin\beta =\dfrac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2} \]
\[ \displaystyle sin\alpha cos\beta =\dfrac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2} \]
\[ \displaystyle cos\alpha cos\beta =\dfrac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2} \]
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
Основные тригонометрические формулы
1.Основы.
sin2a+cos2a=1
seca=1/cosa
csca=1/sina
sec2a-tg2a=1
csc2a-ctg2a=1
2.Сумма углов.
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+cosasinb
sin(a-b)=sinacosb-cosasinb
tg(a+b)=tga+tgb/1-tgatgb=
=ctga+ctgb/ctgactgb-1
tg(a-b)=tga-tgb/1+tgatgb=
=ctgb-ctga/1+ctgactgb
3. Умножение функций.
2sinacosb=sin(a+b)+sin(a-b)
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=cos(a-b)-cos(a+b)
4.Сложение и вычитание.
sina+sinb=2sin(a+b)/2cos(a-b)/2
sina-sinb=2sin(a-b)/2cos(a+b)/2
cosa+cosb=2cos(a+b)/2cos(a-b)/2
cosa-cosb=2sin(a+b)/2sin(b-a)/2
tga+tgb=sin(a+b)/cosacosb
tga-tgb=sin(a-b)/cosacosb
ctga+ctgb=sin(a+b)/sinasinb
ctga-ctgb=sin(b-a)/sinasinb
tga+ctgb=cos(a-b)/cosacosb
ctga-tgb=cos(a+b)/sinasinb
5.Разность квадратов функций
sin2a-cos2b=sin(a+b)sin(a-b)
cos2a-sin2b=cos(a+b)sin(b-a)
cos2a-cos2b=sin(a+b)sin(b-a)
6. Какая-то формула(крутая)
a cosa+b sina=c sin(a+f)
c=Öa2+b2
sinf=a/c
7.Функции нескольких углов.
sin2a=2sinacosa=2tga/1+tg2a
sin3a=3sina-4sin3a
sin4a=cosa(4sina-8sin2a)
cos2a=cos2a-sin2a=2cos2a-1=1-2sina==1-tg2a/1+tg2a=ctga-tga/ctga+tga
cos3a=4cos2a-3cosa
cos4a=8cos4a-8cos2a
tg2a=2tga/1-tg2a=2ctga/ctg2a-1=2/ctga-tga
ctg2a=ctg2a-1/2ctga=1-tg2a/2tga=ctga-tga/2
8.Функции половинного угла.
sina/2= Ö1/2(1-cosa)
cosa/2= Ö1/2(1+sina)
tga/2=1-cosa/sina=sina/1+cosa=Ö1-cosa/1+cosa
ctga/2=sina/1-cosa=1+cosa/sina=Ö1+cosa/1-cosa
9.Понижение степени Sin и Cos.
sin2a=1/2(1-cos2a)
sin3a=1/4(3sina-sin3a)
sin4a=1/8(cos4a-4cos2a+3)
cos2a=1/2(cos2a+1)
cos3a=1/4(cos3a+3cosa)
cos4a=1/8(cos4a+4cos2a+3)
Основные тригонометрические формулы | Рефераты KM.RU
Основные тригонометрические формулы
1.Основы.
sin2a+cos2a=1
seca=1/cosa
csca=1/sina
sec2a-tg2a=1
csc2a-ctg2a=1
2.Сумма углов.
cos(a+b)=cosacosb-sinasinb
cos(a-b)=cosacosb+sinasinb
sin(a+b)=sinacosb+cosasinb
sin(a-b)=sinacosb-cosasinb
tg(a+b)=tga+tgb/1-tgatgb=
=ctga+ctgb/ctgactgb-1
tg(a-b)=tga-tgb/1+tgatgb=
=ctgb-ctga/1+ctgactgb
3. Умножение функций.
2sinacosb=sin(a+b)+sin(a-b)
2cosacosb=cos(a+b)+cos(a-b)
2sinasinb=cos(a-b)-cos(a+b)
4.Сложение и вычитание.
sina+sinb=2sin(a+b)/2cos(a-b)/2
sina-sinb=2sin(a-b)/2cos(a+b)/2
cosa+cosb=2cos(a+b)/2cos(a-b)/2
cosa-cosb=2sin(a+b)/2sin(b-a)/2
tga+tgb=sin(a+b)/cosacosb
tga-tgb=sin(a-b)/cosacosb
ctga+ctgb=sin(a+b)/sinasinb
ctga-ctgb=sin(b-a)/sinasinb
tga+ctgb=cos(a-b)/cosacosb
ctga-tgb=cos(a+b)/sinasinb
5.Разность квадратов функций
sin2a-cos2b=sin(a+b)sin(a-b)
cos2a-sin2b=cos(a+b)sin(b-a)
cos2a-cos2b=sin(a+b)sin(b-a)
6. Какая-то формула(крутая)
a cosa+b sina=c sin(a+f)
c=Öa2+b2
sinf=a/c
7.Функции нескольких углов.
sin2a=2sinacosa=2tga/1+tg2a
sin3a=3sina-4sin3a
sin4a=cosa(4sina-8sin2a)
cos2a=cos2a-sin2a=2cos2a-1=1-2sina==1-tg2a/1+tg2a=ctga-tga/ctga+tga
cos3a=4cos2a-3cosa
cos4a=8cos4a-8cos2a
tg2a=2tga/1-tg2a=2ctga/ctg2a-1=2/ctga-tga
ctg2a=ctg2a-1/2ctga=1-tg2a/2tga=ctga-tga/2
8.Функции половинного угла.
sina/2= Ö1/2(1-cosa)
cosa/2= Ö1/2(1+sina)
tga/2=1-cosa/sina=sina/1+cosa=Ö1-cosa/1+cosa
ctga/2=sina/1-cosa=1+cosa/sina=Ö1+cosa/1-cosa
9.Понижение степени Sin и Cos.
sin2a=1/2(1-cos2a)
sin3a=1/4(3sina-sin3a)
sin4a=1/8(cos4a-4cos2a+3)
cos2a=1/2(cos2a+1)
cos3a=1/4(cos3a+3cosa)
cos4a=1/8(cos4a+4cos2a+3)
a | 00 | 300 | 450 | 600 | 900 |
p/6 | p/4 | p/3 | p/2 | ||
sin a | 0 | 1/2 | Ö2/2 | Ö3/2 | 1 |
cos a | 1 | Ö3/2 | Ö2/2 | 1/2 | 0 |
tg a | 0 | Ö3/3 | 1 | Ö3 | — |
ctg a | — | Ö3 | 1 | Ö3/3 | 0 |
Формулы привидения. | ||||||||
x | p + a | p — a | 2p + a | 2p — a | p /2 + a | p /2 — a | 3/2p + a | 3/2p — a |
sin x | — sin a | sin a | sin a | — sin a | cos a | cos a | — cos a | — cos a |
cos x | — cos a | — cos a | cos a | cos a | — sin a | sin a | sin a | — sin a |
tg x | tg a | — tg a | tg a | — tg a | — ctg a | ctg a | — ctg a | ctg a |
ctg x | ctg a | — ctg a | ctg a | — ctg a | — tg a | tg a | — tg a | tg a |
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://ilib.ru/
Дата добавления: 29.07.2003
