Формулы суммы и разности двух углов – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Формулы сложения выражают синус, косинус, тангенс и котангенс суммы и разности двух углов поворота \(\alpha \ и\ \beta\) через тригонометрические функции этих углов.
- Синус суммы: \(sin \left( {\alpha + \beta } \right) = sin \alpha \cdot cos \beta + cos \alpha \cdot sin \beta\).
- Синус разности: \(sin \left( {\alpha — \beta } \right) = sin \alpha \cdot cos \beta — cos \alpha \cdot sin \beta\).
- Косинус суммы: \(cos(α+β)=cosα \cdot cosβ−sinα \cdot sinβ\).
- Косинус разности: \(cos(α−β)=cosα \cdot cosβ+sinα \cdot sinβ\).
- Тангенс суммы: \(tg \left( {\alpha + \beta } \right) = \large\frac{{tg \alpha + tg \beta }}{{1 — tg \alpha \cdot tg \beta }}\normalsize\).

Вопросы
Найдите значение \(ctg15°\).
Упростите выражение.
\(\sqrt3cos\alpha-2cos(\alpha-\frac{\pi}6)\)
Вычислите.
\(cos15° + sin15° · ctg30°\)
Найдите значение \(sin15°\).
Упростите.
\(\frac{sin(\alpha-\beta)+2cos\alpha\cdot sin\beta}{2cos\alpha\cdot cos\beta-cos(\alpha-\beta)}\)
-
Найдите \(ctg\alpha, \ если \ tg(\alpha+\frac{\pi}4)=0,2\).
 {\circ}\)
{\circ}\)
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены.
 В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Формула — Котангенс суммы и разности
Формула Котангенс суммы и разности
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\mathrm{ctg}(\alpha + \beta) = \frac{\mathrm{ctg}{\alpha} \mathrm{ctg}{\beta} — 1}{\mathrm{ctg}{\beta} + \mathrm{ctg}{\alpha}}\]
\[\mathrm{ctg}(\alpha — \beta) = \frac{\mathrm{ctg}{\alpha} \mathrm{ctg}{\beta} + 1}{\mathrm{ctg}{\beta} — \mathrm{ctg}{\alpha}}\]
Доказательство
 По определению контангенса:
По определению контангенса:\[\mathrm{ctg}(\alpha + \beta) = \frac{\cos(\alpha + \beta)}{\sin(\alpha + \beta)}\]
Из формул косинуса и синуса суммы:
\[\frac{\cos(\alpha + \beta)}{\sin(\alpha + \beta)} = \frac{\cos{\alpha} \cos{\beta} — \sin{\alpha} \sin{\beta}}{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}}\]
\(\sin\alpha \ne 0\) и \(\sin\beta \ne 0\) т.к. при \(\sin\alpha =0\) не определен \(\mathrm{ctg}{\alpha}\) (ввиду деления на ноль), аналогично для \(\sin\beta\). Следовательно, можно разделить числитель и знаменатель дроби на \(\sin\alpha \sin\beta\).
\[\frac{\cos{\alpha} \cos{\beta} — \sin{\alpha} \sin{\beta}}{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}} = \frac{\frac{\cos{\alpha} \cos{\beta}}{\sin{\alpha}\sin{\beta}} — \frac{\sin{\alpha} \sin{\beta}}{\sin{\alpha}\sin{\beta}}}{\frac{\sin{\alpha} \cos{\beta}}{\sin{\alpha}\sin{\beta}} + \frac{\cos{\alpha} \sin{\beta}}{\sin{\alpha}\sin{\beta}}} = \frac{\mathrm{ctg}{\alpha}\mathrm{ctg}{\beta} — 1}{\mathrm{ctg}{\beta} + \mathrm{ctg}{\alpha}}\]
Доказательство контангенса разности аналогично.
 По определению контангенса:
По определению контангенса:\[\mathrm{ctg}(\alpha — \beta) = \frac{\cos(\alpha — \beta)}{\sin(\alpha — \beta)}\]
Из формул косинуса и синуса суммы:
\[\frac{\cos(\alpha — \beta)}{\sin(\alpha — \beta)} = \frac{\cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}}{\sin{\alpha} \cos{\beta} — \cos{\alpha} \sin{\beta}}\]
\(\sin\alpha \ne 0\) и \(\sin\beta \ne 0\) т.к. при \(\sin\alpha =0\) не определен \(\mathrm{ctg}{\alpha}\) (ввиду деления на ноль), аналогично для \(\sin\beta\). Следовательно, можно разделить числитель и знаменатель дроби на \(\sin\alpha \sin\beta\).
\[\frac{\cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}}{\sin{\alpha} \cos{\beta} — \cos{\alpha} \sin{\beta}} = \frac{\frac{\cos{\alpha} \cos{\beta}}{\sin{\alpha}\sin{\beta}} + \frac{\sin{\alpha} \sin{\beta}}{\sin{\alpha}\sin{\beta}}}{\frac{\sin{\alpha} \cos{\beta}}{\sin{\alpha}\sin{\beta}} — \frac{\cos{\alpha} \sin{\beta}}{\sin{\alpha}\sin{\beta}}} = \frac{\mathrm{ctg}{\alpha}\mathrm{ctg}{\beta} + 1}{\mathrm{ctg}{\beta} — \mathrm{ctg}{\alpha}}\]
изменить / сообщить об ошибке
связанные материалы
Формула Синус суммы и разности
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\sin(\alpha + \beta) = \sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}\]
\(\sin(\alpha — \beta) = \sin{\alpha} \cos{\beta} — \cos{\alpha} \sin{\beta}\)
изменить / сообщить об ошибке
Формула Косинус суммы и разности
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\cos(\alpha + \beta) = \cos{\alpha} \cos{\beta} — \sin{\alpha} \sin{\beta}\]
\[\cos(\alpha — \beta) = \cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}\]
изменить / сообщить об ошибке
Формула Тангенс суммы и разности
Входящие величины
\(\alpha\) — произвольный угол \((рад)\)
\(\beta\) — произвольный угол \((рад)\)
\[\mathrm{tg}(\alpha + \beta) = \frac{\mathrm{tg}{\alpha} + \mathrm{tg}{\beta}}{1 — \mathrm{tg}{\alpha} \mathrm{tg}{\beta}}\]
\[\mathrm{tg}(\alpha — \beta) = \frac{\mathrm{tg}{\alpha}- \mathrm{tg}{\beta}}{1 + \mathrm{tg}{\alpha} \mathrm{tg}{\beta}}\]
Доказательство
Докажем сначала тангенс суммы.
 По определению тангенса:
По определению тангенса:\[\mathrm{tg}(\alpha + \beta) = \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)}\]
Из формул косинуса и синуса суммы:
\[\frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} = \frac{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta} — \sin{\alpha} \sin{\beta}}\]
\(\cos\alpha \ne 0\) и \(\cos\beta \ne 0\) т.к. при \(\cos\alpha =0\) не определен \(\mathrm{tg}{\alpha}\) (ввиду деления на ноль), аналогично для \(\cos\beta\). Следовательно, можно разделить числитель и знаменатель дроби на \(\cos\alpha \cos\beta\).
\[\frac{\sin{\alpha} \cos{\beta} + \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta} — \sin{\alpha} \sin{\beta}} = \frac{\frac{\sin{\alpha} \cos{\beta}}{\cos{\alpha}\cos{\beta}} + \frac{\cos{\alpha} \sin{\beta}}{\cos{\alpha}\cos{\beta}}}{\frac{\cos{\alpha} \cos{\beta}}{\cos{\alpha}\cos{\beta}} — \frac{\sin{\alpha} \sin{\beta}}{\cos{\alpha}\cos{\beta}}} = \frac{\mathrm{tg}{\alpha} + \mathrm{tg}{\beta}}{1 — \mathrm{tg}{\alpha}\mathrm{tg}{\beta} }\]
Доказательство тангенса разности аналогично.

\[\mathrm{tg}(\alpha — \beta) = \frac{\sin(\alpha — \beta)}{\cos(\alpha — \beta)}\]
Из формул косинуса и синуса суммы:
\[\frac{\sin(\alpha — \beta)}{\cos(\alpha — \beta)} = \frac{\sin{\alpha} \cos{\beta} — \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}}\]
\(\cos\alpha \ne 0\) и \(\cos\beta \ne 0\) т.к. при \(\cos\alpha =0\) не определен \(\mathrm{tg}{\alpha}\) (ввиду деления на ноль), аналогично для \(\cos\beta\). Следовательно, можно разделить числитель и знаменатель дроби на \(\cos\alpha \cos\beta\).
\[\frac{\sin{\alpha} \cos{\beta} — \cos{\alpha} \sin{\beta}}{\cos{\alpha} \cos{\beta} + \sin{\alpha} \sin{\beta}} = \frac{\frac{\sin{\alpha} \cos{\beta}}{\cos{\alpha}\cos{\beta}} — \frac{\cos{\alpha} \sin{\beta}}{\cos{\alpha}\cos{\beta}}}{\frac{\cos{\alpha} \cos{\beta}}{\cos{\alpha}\cos{\beta}} + \frac{\sin{\alpha} \sin{\beta}}{\cos{\alpha}\cos{\beta}}} = \frac{\mathrm{tg}{\alpha} — \mathrm{tg}{\beta}}{1 + \mathrm{tg}{\alpha}\mathrm{tg}{\beta} }\]
изменить / сообщить об ошибке
Формулы сложения и вычитания для тангенса и котангенса
Формула сложения касательной
На предыдущей странице мы получили тождества сложения для синуса и косинуса:
\[\ грех \ влево ( {\ альфа + \ бета } \ вправо) = \ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета , \]
\[\cos \left( {\alpha + \beta} \right) = \cos \alpha \cos \beta — \sin \alpha \sin \beta .
 \]
\]Предположим теперь, что \(\cos \left( {\alpha + \beta } \right) \ne 0,\) или \(\alpha + \beta \ne \frac{\pi }{2} + \pi n ,\) \(n \in \mathbb{Z}.\) Кроме того, пусть также \(\cos \alpha \ne 0\) и \(\cos \beta \ne 0,\), т. е. \(\ alpha, \beta \ne \frac{\pi }{2} + \pi n,\) \(n \in \mathbb{Z},\), так что мы можем разделить на \(\cos\alpha\cos\ бета.\)
Тогда формула сложения тангенсов будет равна
\[\require{cancel} \tan \left({\alpha + \beta} \right) = \frac{{\sin \left({\alpha + \beta} \right)}}{{\cos\ слева ( {\ альфа + \ бета } \ справа)}} = \ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ соз \ альфа \ соз \ бета — \ грех \ альфа \ грех \ бета}} = \ гидроразрыва {{\ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ соз \ альфа \ соз \ бета}}} }{{\ frac {{\ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta}} {\ cos \ alpha \ cos \ beta}}}} = \ frac {{\ frac {{\ sin \alpha \cancel{\cos\beta}}}{{\cos\alpha\cancel{\cos\beta}}} + \frac{{\cancel{\cos\alpha}\sin\beta}}{{ \cancel{\cos\alpha}\cos\beta}}}}{{\frac{\cancel{\cos\alpha\cos\beta}}}{\cancel{\cos\alpha\cos\beta}} — \ frac {{\ sin \ alpha \ sin \ beta}} {{\ cos \ alpha \ cos \ beta}}}} = \ frac {{\ tan \ alpha + \ tan \ beta}} {{1 — \ tan \ альфа\тангенс\бета}}.
 \]
\]Следовательно,
\[\tan\left( {\alpha + \beta} \right) = \frac{\tan\alpha + \tan\beta}{1 — \tan\alpha\tan\beta}\]
Формула вычитания касательной
Функция тангенса нечетная:
\[\ тан \ влево ( { — \ бета } \ вправо) = \ гидроразрыва {{\ грех \ влево ( { — \ бета } \ вправо)}} {{\ соз \ влево ( { — \ бета } \ вправо )}} = \ frac {{ — \ sin \ beta }} {{\ cos \ beta }} = — \ tan \ beta .\]
Заменяя \(\beta \to -\beta\) в формуле сложения тангенсов, получаем формулу вычитания тангенсов:
\[\ tan \left( {\alpha — \beta} \right) = \frac{{\tan \alpha + \tan \left({ — \beta} \right)}}{{1 — \tan \ alpha \tan \left( { — \beta } \right)}} = \frac{{\tan \alpha — \tan \beta}}{{1 + \tan \alpha \tan \beta }}.\]
Таким образом,
\[\tan\left( {\alpha — \beta} \right) = \frac{\tan\alpha — \tan\beta}{1 + \tan\alpha\tan\beta}\]
Формула сложения котангенса
Аналогичным образом мы можем установить тождество сложения для котангенса.

Пусть \(\sin \left( {\alpha + \beta } \right) \ne 0,\), то есть \(\alpha + \beta \ne \pi n,\) \(n \in \mathbb {Z}.\) Мы также предполагаем, что \(\sin\alpha \ne 0\) и \(\sin\beta \ne 0,\) или \(\alpha ,\beta \ne \pi n,\) \(n \in \mathbb{Z},\), так что мы можем разделить на \(\sin\alpha\sin\beta.\)
Тогда у нас есть
\[\ кроватка \ влево ( {\ альфа + \ бета} \ вправо) = \ гидроразрыва {{\ соз \ влево ( {\ альфа + \ бета} \ вправо)}}} {{\ грех \ влево ( {\ альфа + \ beta } \ right)}} = \ frac {{\ cos \ alpha \ cos \ beta — \ sin \ alpha \ sin \ beta}} {\ sin \ alpha \ cos \ beta + \ cos \ alpha \ sin \ бета}} = \ гидроразрыва {{\ гидроразрыва {{\ соз \ альфа \ соз \ бета — \ грех \ альфа \ грех \ бета}} {{\ грех \ альфа \ грех \ бета}}}} {{\ гидроразрыва {{\ грех \ альфа \ соз \ бета + \ соз \ альфа \ грех \ бета}} {{\ грех \ альфа \ грех \ бета}}}} = \ гидроразрыва {{\ гидроразрыва {{\ соз \ альфа \ соз \beta}}{{\sin\alpha\sin\beta}} — \frac{\cancel{\sin\alpha\sin\beta}}{\cancel{\sin\alpha\sin\beta}}}}{ {\ гидроразрыва {{\ отмена {\ грех \ альфа} \ соз \ бета}} {{\ отмена {\ грех \ альфа} \ грех \ бета}} + \ гидроразрыва {{\ соз \ альфа \ отмена {\ грех \ бета} }}{{\sin \alpha \cancel{\sin\beta} }}}} = \frac{{\cot \alpha \cot \beta — 1}}{{\cot \beta + \cot\alpha }}.
 \]
\]Мы получили следующий результат:
\[\cot\left( {\alpha + \beta} \right) = \frac{\cot\alpha\cot\beta — 1}{\cot\alpha + \cot\beta}\]
Котангенс суммы двух углов также может быть выражен через тангенсы:
\[\cot\left( {\alpha + \beta} \right) = \frac{1 — \tan\alpha\tan\beta}{\tan\alpha + \tan\beta}\]
Формула вычитания котангенса
Сначала заметим, что функция котангенса нечетна:
\[\ кроватка \ влево ( { — \ альфа } \ вправо) = \ гидроразрыва {{\ соз \ влево ( { — \ альфа } \ вправо)}} {{\ грех \ влево ( { — \ альфа} \ вправо )}} = \frac{{\cos \alpha}}{{ — \sin \alpha}} = — \cot \alpha .\]
Теперь мы можем легко вывести формулу вычитания котангенса. Получается заменой \(\beta\to-\beta\) в формуле сложения котангенсов:
\[\ раскладушка \ влево ({\ альфа — \ бета} \ справа) = \ гидроразрыва {{\ раскладушка \ альфа \ раскладушка \ влево ( { — \ бета} \ справа) — 1}} {{\ раскладушка \ альфа + \cot \left( { — \beta } \right)}} = \frac{{ — \cot \alpha \cot \beta — 1}}{{\cot \alpha — \cot \beta}} = \frac {{\cot \alpha \cot \beta + 1}}{{\cot \beta — \cot \alpha}}.
 \]
\]Итак, у нас есть
\[\cot\left( {\alpha — \beta} \right) = \frac{\cot\alpha\cot\beta + 1}{\cot\beta — \cot\alpha}\]
В терминах тангенсов формула вычитания котангенса имеет вид
\[\cot\left( {\alpha — \beta} \right) = \frac{1 + \tan\alpha\tan\beta}{\tan\alpha — \tan\beta}\]
См. решенные проблемы на стр. 2.
Тождества суммы и разности углов
Тождество суммы и разности углов
Мы используем MathJaxВстречаются тригонометрические функции суммы или разности двух углов часто в приложениях. Есть несколько способов подтверждения эти результаты.
Теорема о сумме и разности углов
Следующие тождества верны для всех значений, для которых они определено:
$\sin(A\pm B) = \sin A \cos B \pm \cos A \sin B$ $\cos(A\pm B) = \cos A \cos B \mp \sin A \sin B$ $\tan(A\pm B) = \dfrac{\tan A \pm \tan B}{1 \mp \tan A \tan B}$ $\cot(A\pm B) = \dfrac{\cot A \cot B \mp 1}{\cot B \pm \cot A}$ $\sec(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\csc A \csc B \mp \sec A \sec B}$ $\csc(A\pm B) = \dfrac{\sec A \sec B \csc A \csc B}{\sec A \csc B \pm \csc A \sec B}$ Доказательство: Пусть $P$ будет точкой с координаты $(1,0)$.
 Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*}
Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*}Используя симметричное и пифагорейское тождества, это упрощается, чтобы стать формулой суммы углов для косинуса.
Доказательство формулы разности углов для косинус выглядит следующим образом:
\начать{выравнивать} \cos(A-B) &= \cos(A+(-B)) \\ &= \cos A \cos(-B)-\sin A \sin(-B) \\ &= \cos A \cos B + \sin A \sin B \end{выравнивание}Тогда, используя теорему о кофункциях, мы можем получить формулы для синуса:
\начать{выравнивать} \sin(A \pm B) &= \cos\left( \dfrac{\pi}{2}-(A\pm B)\right) \\ &= \cos\left( \left(\dfrac{\pi}{2}-A\right) \mp B\right) \\ &= \cos\left(\dfrac{\pi}{2}-A\right)\cos B \pm \sin\left(\dfrac{\pi}{2}-A\right)\sin B \\ &= \sin A \cos B \pm \cos A \sin B \end{выравнивание}По результатам формул синуса и косинуса можно вывести еще четыре формулы.
 ♦
♦Формулы также можно вывести с помощью треугольников. Хотя мы ссылаемся на следующий вывод как на доказательство, на самом деле значения углов $A$ и $B$, допускаемые выводом, весьма ограничены, и на самом деле требуется более общее доказательство.
Альтернативное доказательство: Пусть положительный даны углы $A$ и $B$, сумма которых меньше 90 градусов. Построить отрезок $PU$ длины 1. Построить треугольник $TPU$ так, чтобы угол $TPU$ был равен угол $A$, а угол $TUP$ равен дополнению к $A$. Построить описанный прямоугольник $PQRS$ так, что угол $QPT$ равен углу $B$, угол $QPU$ равен сумме углов $A$ и $B$, точка $T$ лежит на сегмент $QR$ и $U$ находятся на сегменте $RS$. Обратите внимание, что угол $RTU$ также равен углу $B$.
Треугольник Соотношения Теорема, имеем:
\начать{выравнивать} \sin(A+B) &= УФ \\ &= RT+QT \\ &= ТУ \cos B + PT \sin B \\ &= \sin A \cos B + \cos A \sin B \end{выравнивание}Доказательство идентичности суммы углов для косинуса похожий.
 Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦
Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦Существует несколько классов удостоверений, которые непосредственные следствия суммы углов и Теорема о разнице. 92 т}$
$\csc 2t = \dfrac{\sec t \csc t}{2}$ Доказательство: Доказательство двойного формула угла для синуса выглядит следующим образом:
\начать{выравнивать} \sin 2t &= \sin (t+t) \\ &= \sin t \cos t + \cos t \sin t \\ &= 2 \sin t \cos t \end{выравнивание}Доказательства формул двойного угла для других пять функций похожи.♦
Теорема о снижении мощности
Следующие тождества верны для всех значений, для которых они определено: 92 t = \dfrac{2}{1-\cos 2t}$
Доказательство: формула синуса, начнем с косинуса двойного угол формулу и заменить квадрат косинуса, используя тождество Пифагора. Полученное уравнение можно решить относительно синусоидального квадрата.
 Доказательства степенных формул для остальных пяти функций
похожи.♦
Доказательства степенных формул для остальных пяти функций
похожи.♦Теорема о половинном угле
Следующие тождества верны для всех значений, для которых они определено:
$\sin\dfrac{t}{2} = \pm\sqrt{\dfrac{1-\cos t}{2}}$ $\cos\dfrac{t}{2} = \pm\sqrt{\dfrac{1+\cos t}{2}}$ $\tan\dfrac{t}{2} = \dfrac{1-\cos t}{\sin t}$ $\cot\dfrac{t}{2} = \dfrac{\sin t}{1+\cos t}$ $\sec\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t+1}}$ $\csc\dfrac{t}{2} = \pm\sqrt{\dfrac{2 \sec t}{\sec t-1}}$ Доказательство: 92 t}{2\sin t\cos t} = \dfrac{\sin t}{\cos t} = \tan t \end{выравнивание}
Подстановка в этот результат дает тангенс Формула половинного угла. Доказательство формулы котангенса аналог.♦
Теорема о произведении суммы
Следующие тождества верны для всех вещественных значений.
$\sin A\sin B=\dfrac12 [(\cos(A-B)-\cos(A+B)]$ $\sin A\cos B=\dfrac12 [(\sin(A+B)+\sin(A-B)]$ $\cos A\cos B=\dfrac12 [(\cos(A+B)+\cos(AB)]$ Доказательство: Расширение и упрощение правая часть каждой формулы с использованием угла Сумма и Теорема о разностях даст левую часть.



 {\circ}\)
{\circ}\) В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен. По определению контангенса:
По определению контангенса: По определению контангенса:
По определению контангенса: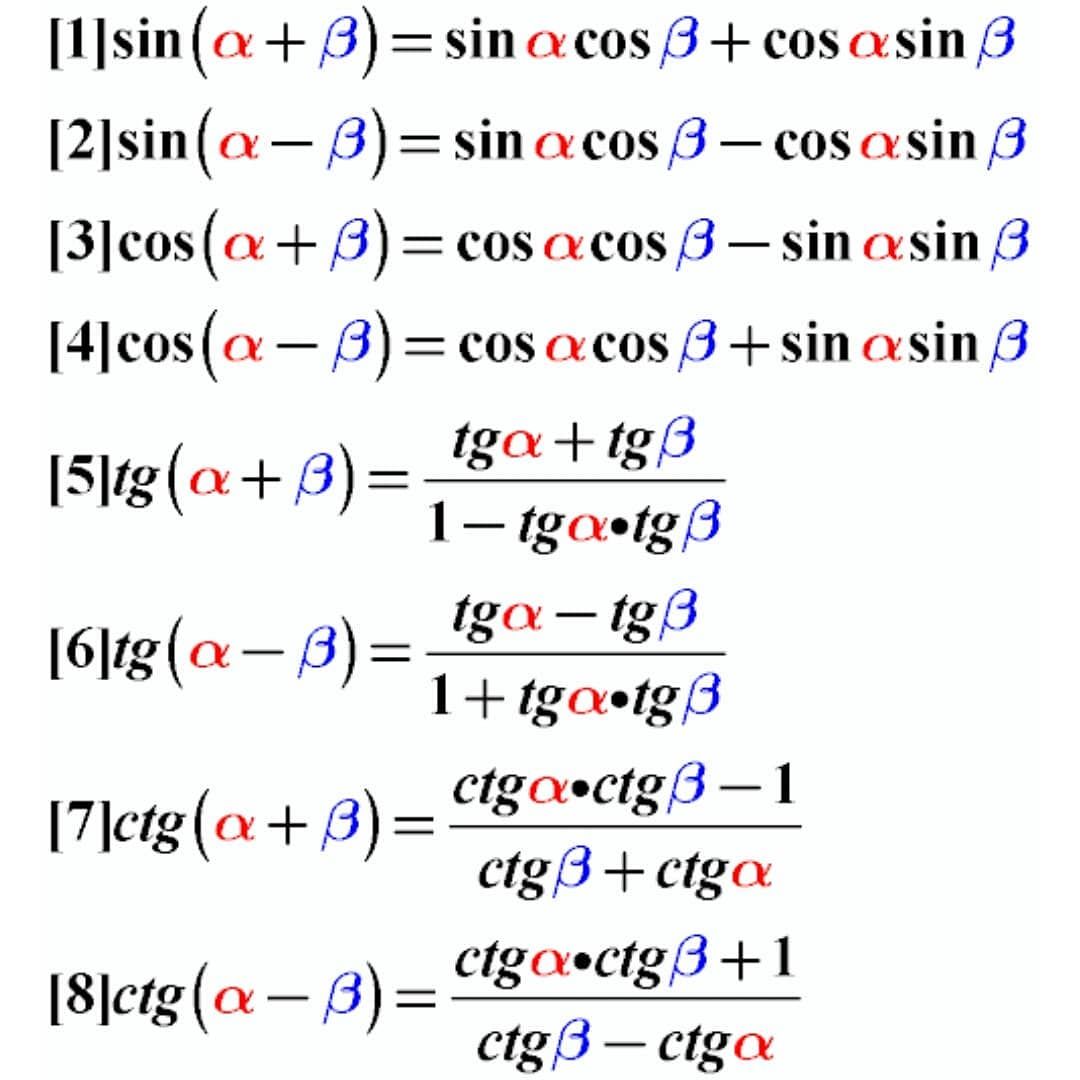 По определению тангенса:
По определению тангенса:
 \]
\] \]
\]
 \]
\] \]
\] Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*}
Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*} ♦
♦ Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦
Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦ Доказательства степенных формул для остальных пяти функций
похожи.♦
Доказательства степенных формул для остальных пяти функций
похожи.♦