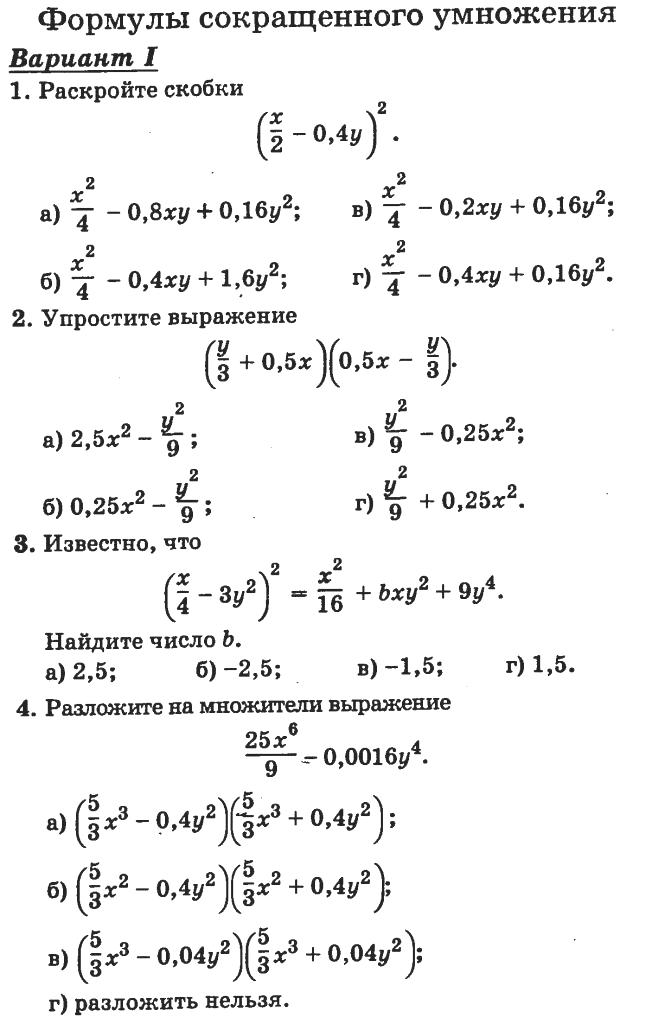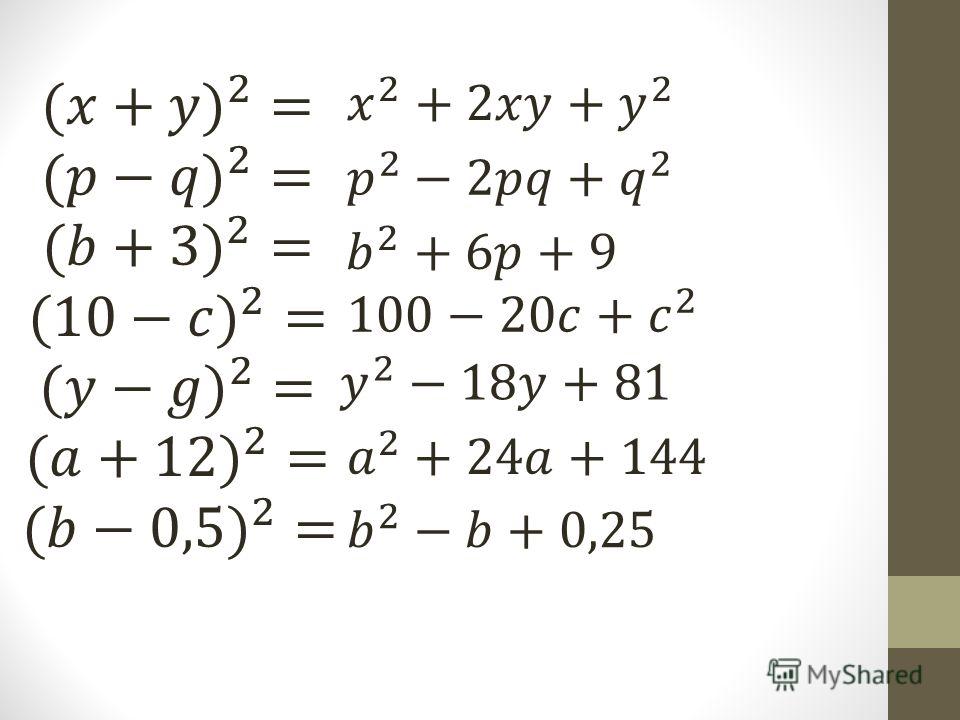Формула сокращенного умножения 7 класс примеры с решениями: Формулы сокращённого умножения — урок. Алгебра, 7 класс.

Формулы сокращённого умножения в задачах повышенной сложности. Ч.2 7 класс онлайн-подготовка на Ростелеком Лицей |

Формулировка темы урока и напоминание теоретического материала

 

Вспомним, какие задачи можно решать с помощью формул сокращенного умножения. Конечно, в первую очередь – это упрощение умножения многочленов. Вторая задача – разложение многочлена на множители. Формулы сокращенного умножения справедливы для любых значений  и , поэтому усложнение задачи во многом определяется именно усложнением выражений  и . Рассмотрим пример.

 

 

Решение уравнений

 

 

Пример 1 – решить уравнение:

 

;

;

 или  или

Рассмотрим первое из полученных уравнений:

; . Данное уравнение не имеет решений, поскольку квадрат любого выражения есть число положительное, а справа стоит число отрицательное.

Рассмотрим второе уравнение:

;

Третье уравнение:

;

Ответ:  или .

Комментарий: для решения данного уравнения нужно сначала разложить левую часть на множители, для этого нужно использовать формулу разности квадратов, причем несколько раз. Напомним, что разность квадратов двух выражений равна произведению их суммы на разность. После того как разложение окончено, нужно вспомнить, что если произведение нескольких множителей равно нулю, то по крайней мере один из этих множителей равен нулю. Исходя из этого факта, приравнять каждую скобку к нулю и из полученных уравнений найти все возможные варианты решения.

Пример 2:

;

 или

Рассмотри первое уравнение:

;

.

Второе уравнение:

;

;

Ответ:  или .

Комментарий: данный пример решается аналогично предыдущему. Сначала нужно разложить левую часть выражения на множители, используя формулу разности квадратов. После этого решить уравнение, зная, что если произведение равно нулю, то хотя бы один из множителей равен нулю.

 

Решение примеров на разложение многочлена на множители

 

 

Пример 4 – разложить на множители:

 

Комментарий: для решения данного задания нужно разложить выражение на множители, пользуясь формулой разности квадратов. Полученные скобки необходимо упростить. Кроме того, можно избавиться от минусов. Для этого вынесем минус из одной скобки и внесем его во вторую.

Пример 5:

.

Данное выражение можно разложить двумя способами. Можно напрямую возводить в квадрат, но к упрощению это не приведет, а можно применить формулу разности квадратов:

Комментарий: после применения формулы в скобках нужно привести подобные члены и получить упрощенное выражение.

Пример 6 – представить выражение в виде квадрата двучлена:

;

.

Комментарий: для решения данного примера необходимо подробно разобрать заданный двучлен и свернуть его по формуле квадрата разности.

Пример 7:

Комментарий: при решении данного примера нужно внимательно разобрать заданное выражение и определить, квадраты каких выражений представлены, после этого проверить удвоенное произведение и свернуть выражение как квадрат разности.

Пример 8:

Комментарий: пример решается аналогично предыдущему, нужно правильно определить квадраты выражений, определить сами выражения, проверить удвоенное произведение и свернуть квадрат разности.

Пример 3:

; ;

 

;

 

 или .

Первое уравнение:

Второе уравнение:

.

Ответ:  или

Комментарий: пример решается аналогично предыдущим: левая часть расписывается по формуле разности квадратов, после этого решается уравнение. Правильность решения данного уравнения можно проверить. Поскольку переменная стоит в квадрате и больше ее в уравнении нет, то если уравнение имеет положительный корень, то оно обязательно имеет такой же отрицательный корень.

 

Решение усложненного примера

 

 

Пример 9: упростить:

 

;

Комментарий: для решения данного примера нужно неоднократно использовать формулу разности квадратов и сворачивать произведение суммы чисел на их разность, чтобы получить простейший результат.

 

Домашнее задание и выводы по уроку

 

 

Вывод: мы рассмотрели различные задачи и закрепили технику применения формул сокращенного умножения, научились решать усложненные задачи и решили много примеров.

 

 

Список литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Егэ по математике (Источник).
2. Интернет-портал Math-prosto.ru (Источник).

 

Домашнее задание

1. а) ; б) ; в)
2. а) ; б) ; в) ;
3. а); б) .

 

Тест Формулы сокращенного умножения (7 класс) онлайн по алгебре

Последний раз тест пройден более 24 часов назад.

Для учителя

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

1. Вопрос 1 из 10

   Допишите равенство: (3a + 2b)

   ² = 9a² + 12ab + …

   • 4b²

   • 8b

   • 2b²

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

2. Вопрос 2 из 10

   Раскройте скобки: (2a + 5)

   ²

   • 4a² + 10a + 25

   • 4a² + 20a + 25

   • 2a² + 20a + 25

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

3. Вопрос 3 из 10

   Возведите в куб двучлен 3х + 2:

   • 27х³ + 54 х² + 36х + 8

   • 27х³ + 18х² + 12х +8

   • 9х³ + 18х + 8

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

4. Вопрос 4 из 10

   Замените звездочку (*) одночленом так, чтобы получилось верное равенство.

   (7x + 1)² = (*) + 14x + 1

   • 7x²

   • 49x²

   • 14x²

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

5. Вопрос 5 из 10

   Разложите на множители: 100 — k

   ⁶:

   • (10 — k³)(10 + k³)

   • (10 — k⁴)(10 + k²)

   • (k³ — 10)(k³ + 10)

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

6. Вопрос 6 из 10

   Представьте в виде степени: 25x

   ² + 40xy + 16y²

   • (25x + 4y)²

   • (5x + 4y)²

   • (25x + 16y)²

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

7. Вопрос 7 из 10

   Выполните возведение в квадрат: (7b + b

   ⁵)²:

   • 49b² + 7b⁶ + b¹⁰

   • 49b² + 14b⁶ + b¹⁰

   • 7b² + 14b⁶ + 7b²

   Подсказка
   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

8. Вопрос 8 из 10

   Замените знак * таким одночленом, чтобы полученное выражение можно было представить в виде квадрата двучлена: * — 28pq + 49q

   ²:

   • 2p²

   • 4

   • 8p²

   • 4p²

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

9. Вопрос 9 из 10

   Упростите выражение: (1 — 3х)(1 — 4х + х

   ²) + (3х — 1)(1 — 5х + х²) + 3х²:

   • -х

   • х

   • -10х

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

10. Вопрос 10 из 10

    Раскройте скобки: (2x

    ³ + 3y²)²

    • 4x⁶ + 12x³y² + 9y⁴

    • 4x⁶ + 6x³y² + 9y⁴

    • 4x³ + 12x³y² + 9y

      4

    Подсказка

    Правильный ответ

    Неправильный ответ

    В вопросе ошибка?

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Эльмира Баймаханова

  10/10

• Даня Орловский

  8/10

• Юра Беляев

  10/10

• Роза Балгабаевна

  10/10

• Анна Поплавская

  10/10

• Ира Шавкунова

  8/10

• Дима Голдобин

  6/10

• Дима Титов

  9/10

• Линар Салимов

  8/10

• Миляуша Гайсина

  7/10

Тест «Формулы сокращенного умножения» (7 класс) с ответами составлен в соответствии с действующей программой, утвержденной министерством. Данная подборка тестов поможет качественно подготовиться к контрольной работе. Задания удобно просматривать в онлайн режиме с любого доступного устройства. Вопросы проверяют знание формул и умение проверять их на практике. С помощью вопросов теста можно быстро проверить свои знания по теме.

Тест по теме «Формулы сокращенного умножения» поможет быстро и качественно оценить знания данной темы, станут отличным помощником для тех, кто хочет подтянуть алгебру.

Рейтинг теста

4

Средняя оценка: 4

Всего получено оценок: 2869.

---

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Ассоциативное свойство умножения — формула, примеры, часто задаваемые вопросы

Ассоциативное свойство умножения утверждает, что способ группировки чисел в задаче на умножение не влияет на произведение этих чисел и не изменяет его. Другими словами, произведение трех и более чисел остается неизменным независимо от того, как они сгруппированы. Давайте узнаем больше об ассоциативном свойстве умножения в этой статье.

1.	Что такое ассоциативное свойство умножения?
2.	Ассоциативное свойство формулы умножения
3.	Ассоциативное свойство умножения и сложения
4.	Часто задаваемые вопросы об ассоциативном свойстве умножения

Что такое ассоциативное свойство умножения?

В соответствии с ассоциативным свойством умножения , если умножить три или более чисел, мы получим один и тот же результат независимо от того, как эти три числа сгруппированы. Здесь под группировкой понимается способ расстановки скобок в данном выражении умножения. Обратите внимание на следующий пример, чтобы понять концепцию ассоциативного свойства умножения. Выражение в левой части показывает, что 6 и 5 сгруппированы вместе, тогда как выражение в правой части группирует 5 и 7 вместе. Однако, когда мы, наконец, умножаем все числа, получается одно и то же.

Ассоциативное свойство формулы умножения

Формула ассоциативности умножения: (a × b) × c = a × (b × c). Эта формула говорит нам, что независимо от того, как расставлены скобки в выражении умножения, произведение чисел остается одним и тем же. Группировка чисел с помощью скобок помогает создавать более мелкие компоненты, что упрощает вычисление умножения. Обратите внимание на следующую формулу ассоциативного свойства умножения.

Давайте поймем формулу с помощью чисел. Например, умножим 2 × 3 × 4 и посмотрим, как доказывается формула ассоциативности умножения с помощью следующих шагов:

• Шаг 1: Сгруппируем 2 и 3 вместе, составив (2 × 3) × 4. Если мы найдем произведение этого выражения, мы получим 6 × 4, что равно 24.
• Шаг 2: Теперь давайте сгруппируем 3 и 4 вместе, чтобы получилось 2 × (3 × 4). Если умножить это выражение, получится 2 × 12, что снова дает произведение 24,9.0058
• Шаг 3: Это означает, что независимо от того, как мы группируем числа в выражении умножения, произведение остается одним и тем же.

Ассоциативное свойство умножения и сложения

Ассоциативное свойство утверждает, что умножение и сложение чисел могут выполняться независимо от того, как они сгруппированы. Например, чтобы добавить 7, 6 и 3, если мы сгруппируем их как 7 + (6 + 3), сумма, которую мы получим, равна 16. Теперь давайте сгруппируем это как (7 + 6) + 3, и мы увидим что сумма снова равна 16. Это ассоциативное свойство сложения, которое применимо и к умножению. Например, давайте умножим 7, 6 и 3 и сгруппируем числа как 7 × (6 × 3). Произведение этих чисел равно 126. Теперь, если мы сгруппируем числа как (7 × 6) × 3, мы получим то же самое произведение, то есть 126. Обратите внимание на следующий рисунок, который показывает ассоциативное свойство умножения и сложения.

Советы по ассоциативному свойству умножения:

Вот несколько важных моментов, связанных с ассоциативным свойством умножения:

• Ассоциативное свойство всегда применяется к 3 или более числам.
• Ассоциативное свойство существует при сложении и умножении и не может быть применено к вычитанию и делению.

☛ Похожие статьи

• Коммутативное свойство умножения
• Свойство мультипликативной идентичности
• Распределительное свойство умножения
• Нулевое свойство умножения
• Ассоциативное свойство дополнения
• Распределительная собственность
• Аддитивное свойство идентичности

 

Примеры ассоциативного свойства умножения

1. Пример 1: Какое из двух выражений эквивалентно 8 × 3 × 4?

   a.

   ) (8 × 3) × 4

   b.) 24 × 4

   c.) 11 × 4

   Решение:

   Продукт данного выражения является 8 × 3 × 4 = 96. Теперь давайте проверим произведение следующих выражений.

   a.) Произведение (8 × 3) × 4 равно 96.

   b.) Произведение 24 × 4 равно 96.

   c.) Произведение 11 × 4 равно 44.

   Следовательно, первые два выражения эквивалентны 8 × 3 × 4. Для первого выражения мы использовали ассоциативное свойство умножения, чтобы сгруппировать вместе 8 и 3, а второй вариант является упрощенной формой первого варианта. Итак, оба верны.

2. Пример 2: Выберите правильное число, чтобы заполнить пробел в выражении: 5 × (4 × 3) = (5 ×___) × 3
   а.) 3
   б.) 4
   c.) 5

   Решение:

   Ассоциативное свойство умножения утверждает, что a × (b × c) = (a × b) × c. Итак, подставив данное уравнение в эту формулу, мы получим в качестве ответа 4. Правильный вариант (b) 4 означает, что произведение обеих сторон будет равно 60, если мы поместим 4 в пропуск.

3. Пример 3: Вставьте пропущенное число в поле.
   10 × (8 × 7) = (10 × 8) × ___
   Решение:

   Согласно ассоциативному свойству умножения: a × (b × c) = (a × b) × c. Подставляя значения в формулу: 10 × (8 × 7) = (10 × 8) × 7

   Следовательно, пропущенное число будет 7, так как произведение обоих выражений равно 560.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по ассоциативному свойству умножения

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы об ассоциативном свойстве умножения

Что такое ассоциативное свойство умножения в математике?

Ассоциативное свойство умножения гласит, что произведение трех или более чисел остается одним и тем же независимо от того, как числа сгруппированы. Например, 3 × (5 × 6) = (3 × 5) × 6. Здесь, как бы ни группировались числа, произведение обоих выражений остается равным 90.

Что такое ассоциативное свойство формулы умножения?

Формула ассоциативного свойства умножения записывается как a × (b × c) = (a × b) × c. Это означает, что группировка любых трех и более чисел не влияет на их произведение.

Что такое ассоциативное свойство умножения и сложения?

Свойство ассоциативности относится к сложению и умножению, что означает, что сложение и умножение чисел можно выполнять независимо от того, как они сгруппированы. Ассоциативное свойство сложения записывается как: a + (b + c) = (a + b) + c, что означает, что сумма любых трех или более чисел не изменится, даже если изменить группировку чисел. Точно так же ассоциативное свойство умножения записывается как: a × (b × c) = (a × b) × c, что означает, что произведение любых трех или более чисел остается неизменным даже после того, как они были сгруппированы в разные группы. путь.

Приведите пример ассоциативного свойства умножения.

Ассоциативность умножения можно понять на примере любых трех чисел. Если мы умножим (4 × 2) × 10, мы получим произведение как 8 × 10 = 80. Теперь, если мы сгруппируем эти числа как 4 × (2 × 10), мы все равно получим произведение как 4 × 20 = 80. Это доказывает ассоциативность умножения.

Что такое ассоциативное свойство умножения целых чисел?

Ассоциативное свойство умножения целых чисел гласит, что произведение трех и более целых чисел не меняется, даже если числа сгруппированы по-разному. Например, 11 × (5 × 2) = (11 × 5) × 2. Здесь произведение обоих выражений равно 110,9.0005

В чем разница между коммутативным и ассоциативным свойством умножения?

Коммутативное свойство умножения гласит, что изменение порядка чисел не меняет произведения заданных чисел. Например, 6 × 8 = 8 × 6 = 48. Ассоциативное свойство умножения гласит, что изменение группировки чисел не меняет произведения данных чисел. Например, 7 × (2 × 3) = (7 × 2) × 3 = 42.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист свойств умножения

Использование операторов вычисления в формулах Excel

Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно… Меньше

Операторы определяют тип вычисления, которое необходимо выполнить для элементов формулы. Excel следует общим математическим правилам для вычислений, а именно Скобки , Экспоненты , Умножение и Деление и Сложение и вычитание или аббревиатура PEMDAS (Пожалуйста, извините, моя дорогая тетя Салли). Использование круглых скобок позволяет изменить порядок вычислений.

Типы операторов. Существует четыре различных типа операторов вычисления: арифметический , сравнение , конкатенация текста и ссылка .

• org/ListItem»>

  Арифметические операторы

  Для выполнения основных математических операций, таких как сложение, вычитание, умножение или деление; комбинировать числа; и получить числовые результаты, используйте следующие арифметические операторы.

  Арифметический оператор	Значение	Пример
  + (плюс)	Дополнение	=3+3
  – (знак минус)	Вычитание Отрицание	=3–3 =-3
  * (звездочка)	Умножение	=3*3
  / (косая черта)	Отдел	= 3/3
  % (знак процента)	Процент	93

• org/ListItem»>

  Операторы сравнения

  Вы можете сравнить два значения с помощью следующих операторов. Когда два значения сравниваются с помощью этих операторов, результатом является логическое значение — либо ИСТИНА, либо ЛОЖЬ.

  Оператор сравнения	Значение	Пример
  = (знак равенства)	равно	=А1=В1
  > (знак больше)	Больше	=А1>В1
  < (знак меньше)	Менее	=А1<В1
  >= (знак больше или равно)	Больше или равно	=А1>=В1
  <= (знак меньше или равен)	Меньше или равно	=А1<=В1
  <> (без знака равенства)	Не равно	=А1<>В1

• org/ListItem»>

  Оператор конкатенации текста

  Используйте амперсанд ( и ), чтобы объединить (объединить) одну или несколько текстовых строк для создания единого фрагмента текста.

  Текстовый оператор	Значение	Пример
  и (амперсанд)	Соединяет или объединяет два значения для создания одного непрерывного текстового значения	=»Север»&»ветер» приводит к «Борей». Где A1 содержит «Фамилия», а B1 содержит «Имя», = A1 &», «& B1 приводит к «Фамилия, Имя».

• Эталонные операторы

  Объедините диапазоны ячеек для вычислений со следующими операторами.

  Справочный оператор	Значение	Пример
  : (двоеточие)	Оператор диапазона, который создает одну ссылку на все ячейки между двумя ссылками, включая две ссылки. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт