Квадратное уравнение общий вид, формула дискриминанта, примеры и алгоритмы нахождения корней полных и неполных уравнений с объяснениями » Kupuk.net
Независимо от того, в каком классе проходят уроки алгебры – математическом или обычном – квадратное уравнение изучается почти сразу после освоения всех видов своего простого линейного аналога, будучи «следующим уровнем сложности». Вычисление и поиск верного ответа не представляют трудностей, достаточно запомнить алгоритм решения и следовать ему.
Наравне с выражениями с комплексными числами и функциями с двумя переменными, алгебра поначалу заставит ученика изрядно поломать голову вне зависимости от возраста и склада ума.
Отчаявшиеся понять данный раздел науки могут использовать решебник и онлайн-калькулятор, выкладываемые в интернете от разных авторов в различном оформлении — на вкус читателя.
Примеры с переменной в квадрате – хорошие задания для тренировки навыков счета. В математических дисциплинах квадратное уравнение нередко выступает промежуточным шагом к доказательству теорем.
- Дискриминант
- Корни квадратного уравнения
- Полное и неполное квадратное уравнение
- Решение квадратных уравнений
- Стандартный алгоритм решения через дискриминант
- Теорема Виета
- График квадратного уравнения
- Квадратные уравнения – примеры и подробные решения
- Полное решение с двумя числами
- Единственный корень в уравнении
- Отсутствие целевых точек
- Как решать систему уравнений с квадратами
Дискриминант
Изучаемое выражение имеет стандартный вид:
ax2 + bx + c = 0
Все три слагаемых имеют коэффициенты, способные принимать любые значения, но при переменной в квадрате он не должен равняться 0, иначе уравнение перестает быть квадратным.
Например, уравнение 2×2 + 2 = 0 идентично выражению 2×2 + 0x + 2 = 0.
Части равенства справа от знака равенства переносятся влево с противоположным знаком:
6×2 = 8x — 4
6×2 — 8x + 4 = 0
Разобрать квадратное уравнение поможет дискриминант (D). Этот вспомогательный показатель через сложные расчеты позволит найти корни выражения или обнаружить невозможность решения.
Этот вспомогательный показатель через сложные расчеты позволит найти корни выражения или обнаружить невозможность решения.
Вывод формулы выполняется благодаря манипуляции с числовыми показателями:
D = b2 — 4ac
Например, в выражении 5×2 — 7x + 2 = 0
D равен: (-7)2 — 4*5*2 = 49 — 40 = 9.
Определение дискриминанта подскажет количество корней:
D>0: два корня;
D=0: один корень;
D<0: нет решения.
Связано это с тем, что в процессе решения дискриминант придется возводить под квадратный корень — √(D) – а отрицательные числа из него не выводятся.
Корни квадратного уравнения
Завершающий шаг – вывод ответов путем вычислений. Как решить уравнение – зависит от количества корней.
Как решить уравнение – зависит от количества корней.
1. Если ответа 2, их нахождение выполнится через формулы:
2. Когда корень один, дискриминант уже не нужен (ведь √(0) = 0), и решать головоломку проще:
3. В случае, когда решения нет, вычислять ничего не нужно.
Далеко не все способы требуют долгих расчетов. Ученым-математиком из Франции Франсуа Виетом была выведена закономерность, раскрывающая удивительные свойства (коэффициентов):
Уникальна теорема Виета тем, что под ее определение подходят уравнения — приведенные там, где множитель при x2 равен 1.
Например:
Сумма корней равна –b, ведь сложение x1 и x2 приводит к такому ответу:
Произведение обоих ответов происходит по аналогичному принципу:
Способы решения заданий с переменными в квадрате не являются специфическими – даже неприведенные выражения можно решить данной теоремой.
Как пример: 2×2 — 6x + 9 = 0 при делении на коэффициент при x2 (а=2) примет вид x2 — 3x + 4,5 = 0 – и вполне годится для решения методикой французского ученого.
Другой метод того, как решать вариант с а≠1 – делить на a сумму и произведение корней:
2×2-5x+2=0
х1+ х2=5/2 =2,5
х1* х2=2/2 = 1
х1=2, х2=0,5.
Полное и неполное квадратное уравнение
Выражение ax2 + bx + c = 0 считается полным, если содержит все три коэффициента. Если есть слагаемые, равные 0, оно становится неполным.
Если есть слагаемые, равные 0, оно становится неполным.
Неполное квадратное уравнение решается гораздо легче своего полного аналога. Нахождение корней не вызывает трудностей и предполагает свои особенности в поиске ответа.
Самый простой способ – разложение на множители.
2×2 — 5 x = 0 — неполное, так как с = 0.
x*(2x — 5) = 0
х1 = 0
2x — 5 = 0
х2 = 2,5.
Когда отсутствует bx, отыскать ответ еще легче:
x2 — 9 = 0 (здесь b = 0)
(x+3)*(x-3) = 0
или: x2 = 9
х1 = 3, х2 = -3.
Решение квадратных уравнений
Способы решения разнообразны. Состав слагаемых определяет, как находить верный ответ.
Самые легкие – разложение на множители.
Пример:
x2 + 3x — 28 = 0.
Достаточно решить, что 28 = (-4)*7, а 3х = 7х — 4х;
Многочлен x2 + 7x — 4x — 28 = 0 можно представить в виде (x + 7)(x — 4) = 0;
Только два значения способны выполнить условие равенства: -7 и 4.
Вариант сложнее – вывод формулы полного квадрата:
4×2 + 8x + 4 — 4 — 32 = 0
Из 4×2 + 8x возможен многочлен 4×2 + 8x + 4, способный превратиться в (2x + 2)2
Сформировать 4×2 + 8x — 32 = 0 в более компактный вид:
4×2 + 8x +4 — 4 — 32 = 0
(2x + 2)2 — 36 = 0
Cвободное число переходит в правую часть:
Но не все уравнения удается преобразовать в удобную версию. Самые распространенные способы:
Стандартный алгоритм решения через дискриминант
2×2 + 5x — 3 = 0
Найти D:
D = 52 — 4∗2∗(-3) = 25 + 24 = 49
Вычислить корни
Теорема Виета
2×2 + 5x — 3 =0
Из суммы корней и произведения образовать пропорцию
Нахождение ответов подбором и подсчетом:
-3 + 0,5 = -2,5
-3∗0,5 = -1,5
Помимо рядовых вычислений, алгебра предусматривает графический путь – минимум расчетов и чертежи на геометрической плоскости (системе координат).
График квадратного уравнения
В отличие от рассмотренных выше вариантов, построение графика позволит наглядно решить уравнение. Здесь оно предстает в виде системы двух функций – выражений с двумя переменными.
Стандартная формула ax2 + bx + c = 0 принимает иной вид:
или ax2 = -bx -c.
Общие точки параболы и линии станут ответами на задачу.
Квадратные уравнения – примеры и подробные решения
Нахождение ответа через стандартный алгоритм с дискриминантом и ее оформление в приведенное выражение уже рассмотрены, лишь графический метод нуждается в подробном рассмотрении – наглядном свидетельстве либо наличия корней, либо отсутствия оных.
Полное решение с двумя числами
Равенство x2 + 2x — 3 = 0 аналогично удобному для графика аналогу x2 = -2x + 3
На плоскость наносится система двух функций:
Пересечения графиков на точках [1;1] и [-3;9] являются решением задачи. Если нужны были данные по переменной x, воспользоваться нужно ими.
Если нужны были данные по переменной x, воспользоваться нужно ими.
Ответ: 1 и -3.
Единственный корень в уравнении
Подобно примеру выше, выражение 3×2 + 6x + 3 = 0 преобразуется в систему:
Здесь только 1 точка касается обоих графиков – [-1;3]. Координата x – корень уравнения.
Ответ: х = 1.
Отсутствие целевых точек
Уравнение и система
на координатной плоскости не располагают общими отметками.
Как решать случай с несовпадением графиков? Это невозможно.
Ответ: нет корней.
Как решать систему уравнений с квадратами
Квадратные уравнения с двумя переменными нередко предстают в виде системы. Их решение потребует больше усилий и времени, но нахождение ответа все еще возможно.
Их решение потребует больше усилий и времени, но нахождение ответа все еще возможно.
Первый метод уже рассмотрен в разделе выше – графический. Процесс неизменен:
Разбить уравнения на более простые.
Составить функцию с каждым на общей системе координат.
Точки пересечения станут корнями уравнения.
Второй способ – подстановка одного выражения в другое:
К системе подходит следующий алгоритм решения:
1. Представить одну переменную в составе другой:
2. Подставить выраженную переменную x в другое выражение:
3. Решить выражение как обычное квадратное уравнение:
Комбинация ответов занимает много места – дискриминант не всегда удается вывести из-под знака корня:
Третий способ – введение новых переменных. Актуален, когда подстановка займет много времени и поможет упросить вывод формулы.
Обозначить новые переменные:
Использовать их в решении, заменив ими неудобные множители:
Итог – два набора данных
или
Продолжить «расшифровку» с полученными парами чисел, создав и решив стандартное уравнение.
Первый вариант:
Здесь на выходе две подсистемы.
Второй вариант:
Корни при данном раскладе отсутствуют. Решение – первая подборка.
Ответ: х1 = (1;3), х2 = (3;1).
1 корень дискриминант
1 корень дискриминантВы искали 1 корень дискриминант? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 формула дискриминанта, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 корень дискриминант».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 корень дискриминант».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 корень дискриминант,2 формула дискриминанта,2 формулы дискриминанта,b корень из дискриминанта,d 0 формула,d1 дискриминант,d1 дискриминант формула,d1 как найти,d1 формула,d1 формула дискриминанта,x1 x2 дискриминант,x1 дискриминант,алгебра дискриминант,все о дискриминанте,все формулы дискриминанта,вторая формула дискриминанта,вычисление дискриминанта,вычислить дискриминант,д1 дискриминант,две формулы дискриминанта,дескрименант формула,дескриминант,дискременант,дискреминант,дискрименант,дискриминант,дискриминант 0,дискриминант 0 формула,дискриминант 1,дискриминант 1 как найти,дискриминант 1 корень,дискриминант 1 корень формула,дискриминант 1 формула,дискриминант 1 формула д1,дискриминант 2,дискриминант 2 формула,дискриминант d1,дискриминант d1 формула,дискриминант k,дискриминант k2 ac,дискриминант x1,дискриминант x1 x2,дискриминант x1 x2 формула,дискриминант алгебра,дискриминант без с,дискриминант больше нуля,дискриминант в каком классе проходят,дискриминант все формулы,дискриминант вычислить,дискриминант д1,дискриминант д1 формула,дискриминант деленный на 4 формула,дискриминант для четного b,дискриминант и как найти корни,дискриминант и корни,дискриминант и корни формулы,дискриминант из 1,дискриминант икс 1 и икс 2,дискриминант к,дискриминант как найти,дискриминант как найти х,дискриминант как решать,дискриминант как считается,дискриминант квадратного уравнения,дискриминант квадратного уравнения формула,дискриминант квадратное уравнение,дискриминант квадратные уравнения,дискриминант когда равен 1,дискриминант корень,дискриминант корень 1,дискриминант корни,дискриминант корни формула,дискриминант математика,дискриминант матрицы как найти,дискриминант меньше нуля,дискриминант меньше нуля формула,дискриминант меньше нуля что значит,дискриминант неполный,дискриминант ноль,дискриминант один,дискриминант половинный,дискриминант при 0,дискриминант при четном b,дискриминант пример,дискриминант примеры,дискриминант примеры для решения,дискриминант примеры с решением,дискриминант равен,дискриминант равен 0,дискриминант равен 0 как найти,дискриминант равен 0 как найти корень,дискриминант равен 0 квадратное уравнение,дискриминант равен 0 сколько корней,дискриминант равен 0 формула,дискриминант равен 0 формула корня,дискриминант равен 1,дискриминант равен 1 формула,дискриминант равен нулю,дискриминант равен нулю формула,дискриминант решение,дискриминант решение квадратных уравнений,дискриминант решение уравнений,дискриминант решить,дискриминант с минусом,дискриминант сокращенный,дискриминант таблица,дискриминант тема,дискриминант теорема,дискриминант уравнение,дискриминант уравнения,дискриминант формула,дискриминант формула 0,дискриминант формула 1 корень,дискриминант формула 2,дискриминант формула д1,дискриминант формула если 0,дискриминант формула корней,дискриминант формула примеры,дискриминант формула примеры и решение с объяснением,дискриминант формула х1,дискриминант формула х1 х2,дискриминант формула через k,дискриминант формулы,дискриминант формулы и корни,дискриминант формулы х1 х2,дискриминант х1 формула,дискриминант х1 х2 формула,дискриминант через k формула,дискриминант через к,дискриминант четный,дискриминант что такое,дискриминант что это,дискриминант что это такое,дискриминант это,дискриминант это что,дискриминанта,дискриминанта уравнения,дискриминанта формула д1,дискриминантное уравнение,дискриминанты,дискриминация формула,дискримінант,дискримінант формула,если д равен 0,если дискриминант,если дискриминант 0 формула,если дискриминант 1,если дискриминант больше нуля,если дискриминант меньше 0,если дискриминант равен,если дискриминант равен 0 как найти корень,если дискриминант равен 0 какая формула,если дискриминант равен 1,если дискриминант равен 1 какая формула,если дискриминант равен нулю какая формула,если дискриминант равен нулю то как найти корень,задачи дискриминант,задачи с дискриминантом,как вычислить дискриминант,как вычисляется дискриминант,как дискриминант считается,как искать дискриминант,как найти 1 дискриминант,как найти d1,как найти x если дискриминант равен 0,как найти x через дискриминант,как найти x1 и x2 в дискриминанте,как найти дискриминант,как найти дискриминант 1,как найти дискриминант и х1 и х2,как найти дискриминант квадратного уравнения,как найти дискриминант равен 0,как найти дискриминант формула,как найти дискриминант х,как найти дискриминант х1 и х2,как найти дискриминант через k,как найти дискриминант через х,как найти корень дискриминанта,как найти корень если дискриминант равен 0,как найти корень квадратного уравнения если дискриминант равен 0,как найти корни дискриминанта,как найти корни квадратного уравнения через дискриминант,как найти корни уравнения через дискриминант,как найти х дискриминант,как найти х если дискриминант равен 0,как найти х через дискриминант,как найти х через дискриминант формула,как найти х1 и х2 дискриминант,как найти через k дискриминант,как найти через дискриминант x,как находится дискриминант,как находится дискриминант формула,как находить дискриминант,как находить дискриминант формула,как посчитать дискриминант,как решается дискриминант,как решать дискриминант,как решать дискриминант примеры,как решать дискриминантные уравнения,как решать квадратное уравнение через дискриминант,как решать квадратные уравнения через дискриминант,как решать по дискриминанту,как решать уравнение через дискриминант,как решать уравнения с дискриминантом,как решать уравнения через дискриминант,как решать через дискриминант,как решать через дискриминант 1,как решать через дискриминант формула,как решаются квадратные уравнения через дискриминант,как решить дискриминант,как решить дискриминантное уравнение,как решить уравнение с дискриминантом,как решить уравнение через дискриминант,как решить через дискриминант,как считается дискриминант,как считать дискриминант,как через дискриминант найти корни,какая формула если дискриминант равен 0,какая формула если дискриминант равен 1,какая формула если дискриминант равен нулю,какая формула когда дискриминант равен 0,какая формула при дискриминанте 0,квадратное уравнение дискриминант,квадратное уравнение дискриминант равен 0,квадратное уравнение примеры с решением через дискриминант,квадратное уравнение решение через дискриминант,квадратное уравнение с дискриминантом,квадратное уравнение через дискриминант,квадратное уравнение через дискриминант решение,квадратные уравнения дискриминант,квадратные уравнения дискриминант равен нулю,квадратные уравнения примеры с дискриминантом,квадратные уравнения через дискриминант,когда дискриминант равен 0 какая формула,когда дискриминант равен 1,когда дискриминант равен нулю формула,корень дискриминант,корень дискриминанта,корень дискриминанта формула,корень из дискриминанта,корень из дискриминанта формула,корень квадратного уравнения через дискриминант формула,корень при дискриминанте равном 0,корни дискриминант,корни дискриминанта,корни дискриминанта формула,корни из дискриминанта,корни уравнения через дискриминант,корни через дискриминант,математика дискриминант,может ли квадратное уравнение с целыми коэффициентами иметь дискриминант 23,найдите дискриминант уравнения,найти дискриминант,найти дискриминант квадратного уравнения,нахождение дискриминанта,нахождение дискриминанта формула,нахождение корней через дискриминант,нахождение корней через дискриминант формула,неполный дискриминант,нулевой дискриминант,определение дискриминанта,поиск дискриминанта,половинный дискриминант,половинный дискриминант формула,правила дискриминанта,правило дискриминанта,при дискриминанте равном 0,при дискриминанте равном 0 формула,пример дискриминант,пример дискриминанта,пример решения формула дискриминанта,пример с дискриминантом,пример формула дискриминанта,примеры дискриминант,примеры дискриминанта,примеры на дискриминант,примеры на дискриминант 9 класс,примеры по алгебре с дискриминантом,примеры решение квадратных уравнений через дискриминант,примеры решение уравнений через дискриминант,примеры с дискриминантом,примеры с дискриминантом по алгебре,примеры уравнения с дискриминантом примеры,примеры формула дискриминанта,примеры через дискриминант,равен х если дискриминант равен 0,решение дискриминант,решение дискриминанта,решение дискриминанта примеры,решение квадратного уравнения через дискриминант,решение квадратного уравнения через дискриминант формулы,решение квадратных уравнений дискриминант,решение квадратных уравнений через дискриминант,решение по дискриминанту,решение с дискриминантом,решение уравнений дискриминант,решение уравнений с дискриминантом,решение уравнений через дискриминант,решение уравнения через дискриминант,решение через дискриминант,решение через дискриминант формула,решить дискриминант,решить уравнение через дискриминант,свойства дискриминанта,сокращенная дискриминанта формула,сокращенная формула дискриминанта,сокращенный дискриминант,сокращенный дискриминант формула,таблица дискриминант,таблица дискриминанта,таблица дискриминантов,таблица дискриминантов по алгебре,тема дискриминант,теорема дискриминант,теорема дискриминант формула,теорема дискриминанта,уравнение дискриминант,уравнение дискриминанта,уравнение дискриминанта примеры решения,уравнение дискриминанта формула,уравнение с дискриминантом,уравнение с дискриминантом пример,уравнение с дискриминантом формула,уравнение через дискриминант,уравнение через дискриминант примеры,уравнение через дискриминант решить,уравнения дискриминант,уравнения дискриминанта,уравнения на дискриминант,уравнения с дискриминантом,уравнения с дискриминантом как решать,уравнения с дискриминантом примеры,уравнения через дискриминант,уравнения через дискриминант примеры,формула 0 дискриминанта,формула d 0,формула d1,формула d1 дискриминант,формула x1 x2 дискриминант,формула вычисления дискриминанта,формула д1 дискриминант,формула д1 дискриминант к,формула д1 дискриминанта,формула дескрименант,формула дискрименанта,формула дискриминант 0,формула дискриминант деленный на 4,формула дискриминант равен 1,формула дискриминант равен нулю,формула дискриминанта,формула дискриминанта 0,формула дискриминанта 1,формула дискриминанта 1 через k,формула дискриминанта 2,формула дискриминанта d1,формула дискриминанта вторая,формула дискриминанта д1,формула дискриминанта деленного на 4,формула дискриминанта для 0,формула дискриминанта для четных чисел,формула дискриминанта если он равен 0,формула дискриминанта и его,формула дискриминанта и его корней,формула дискриминанта и его корней при 0,формула дискриминанта и его корней через k,формула дискриминанта и корней,формула дискриминанта и нахождения корней,формула дискриминанта и х1,формула дискриминанта и х1 х2,формула дискриминанта квадратного уравнения,формула дискриминанта корня,формула дискриминанта нахождения корней,формула дискриминанта при 0,формула дискриминанта при b четном,формула дискриминанта при четном b,формула дискриминанта пример,формула дискриминанта пример решения,формула дискриминанта примеры,формула дискриминанта равного 0,формула дискриминанта сокращенная,формула дискриминанта сокращенного,формула дискриминанта х1 х2,формула дискриминанта через k,формула дискриминанта через к,формула дискриминанта четверти,формула дискриминанта четная,формула дискриминанта четного,формула дискриминация,формула дискримінант,формула дискримінанта,формула дискримінанту,формула для дискриминанта,формула для дискриминанта 0,формула для нахождения дискриминанта,формула если дискриминант 0,формула если дискриминант равен 0,формула как найти дискриминант,формула квадратного уравнения дискриминант,формула корень дискриминанта,формула корень из дискриминанта,формула корней дискриминанта,формула корня дискриминанта,формула корня если дискриминант равен 0,формула нахождения x1 и x2 через дискриминант,формула нахождения дискриминанта,формула нахождения дискриминанта и корней,формула нахождения корней дискриминанта,формула неполного дискриминанта,формула нулевого дискриминанта,формула отрицательного дискриминанта,формула половинного дискриминанта,формула при дискриминанте 0,формула при дискриминанте равном 0,формула решения квадратного уравнения через дискриминант,формула сокращенного дискриминанта,формула х в дискриминанте,формула х1 дискриминант,формула х1 и х2 дискриминант,формула х1 и х2 при дискриминанте,формула четверти дискриминанта,формула четного дискриминанта,формулы 2 дискриминанта,формулы дискриминанта,формулы дискриминанта 1,формулы дискриминанта 1 через k,формулы дискриминанта 2,формулы дискриминанта все,формулы дискриминанта и корней,формулы дискриминанта корней,формулы дискриминанта при 0,формулы дискриминанта через к,формулы дискриминантов,формулы для дискриминанта,формулы корней дискриминанта,формулы корней квадратного уравнения дискриминант,формулы нахождения дискриминанта,формулы с дискриминантом,формулы х1 х2 дискриминант,функция дискриминанта,чему равен дискриминант,чему равен дискриминант 1,чему равен дискриминант квадратного уравнения,через дискриминант,четверть дискриминанта,четверть дискриминанта формула,четная формула дискриминанта,четный дискриминант,четный дискриминант формула,что делать если дискриминант равен 1,что если дискриминант меньше нуля,что если дискриминант равен 1,что такое в алгебре дискриминант,что такое в математике дискриминант,что такое дискриминант,что такое дискриминант в алгебре,что такое дискриминант в математике.
Решить задачу 1 корень дискриминант вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Решение квадратных уравнений: формула, примеры
Решение квадратных уравнений представляет собой решение уравнения вида: a·x2+b·x+c=0,
где x – переменная, a, b и c – коэффициенты квадратного уравнения.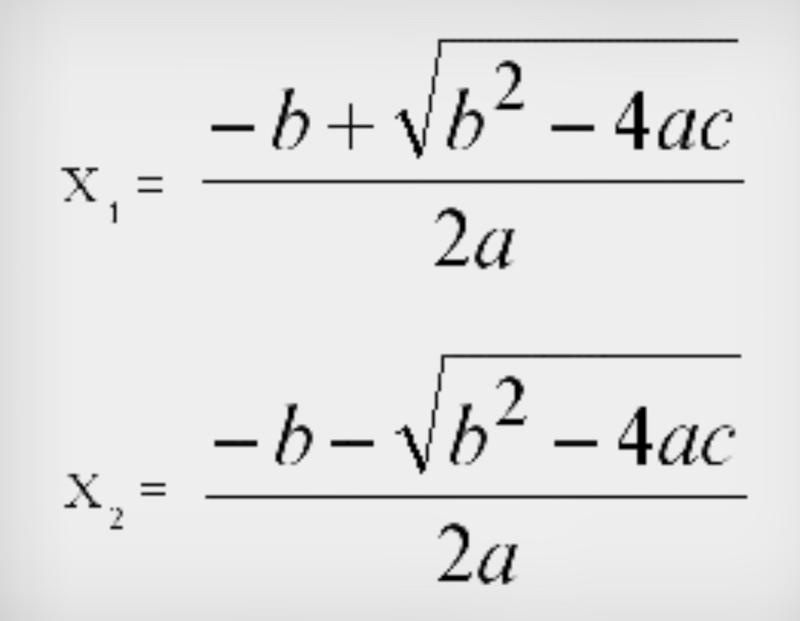 При этом:
При этом:
a — первый (старший) коэффициент, который не равен нулю (a ≠ 0),
b – второй коэффициент,
c — свободный член.
Важно: если квадратное уравнение имеет вид a·x2–b·x–c=0, то второй коэффициент будет равен (–b), а свободный член (–c), то есть в качестве коэффициентов будут отрицательные числа.
Также квадратное уравнение называют уравнением второй степени, так как оно представляет собой уравнение, содержащее переменную во второй степени.
Примеры квадратного уравнения: 9x2+16x+2=0; 7x2+3x+11=0 и т.п.
Найти корень уравнения — значит найти такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Решить квадратное уравнение — значит найти все его корни или доказать, что их не существует.
| x =( -b ± √D)/2a, где D = b − 4ac (D-дискриминант) |
Таким образом, решение квадратного уравнения сводится к нахождению от 0 до 2 корней в зависимости от значения дискриминанта (возможно Вас заинтересует как находить корни):
| D>0 — уравнение имеет 2 корня: x1 =( -b+√D)/2a, x2 =( -b-√D)/2a D=0 — уравнение имеет 1 корень: x =( -b)/2a D<0 — уравнение не имеет корней |
При решении квадратных уравнений важно помнить законы математики:
- когда мы переносим слагаемое из одной части уравнения в другую, оно меняют знак на противоположный;
- если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение.
 Для данного действия нужно уметь находить НОК и НОД.
Для данного действия нужно уметь находить НОК и НОД.
Пример 1. D > 0, уравнение имеет 2 различных корня:
2x2 + 7x — 4 = 0
a = 2, b = 7, c = -4
D = 72 — 4 • 2 • (- 4) = 81 > 0
x1 = (-7 — 9) / (2•2) = — 4
x2 = (-7 + 9) / (2•2) = 1/2
Пример 2. D = 0, уравнение имеет один корень:
x2 — 4x + 4 = 0
D = (-4)2 — 4 • 1 • 4 = 0
x =(-4 ± 0 ) / (2•1) = 2
Пример 3. D < 0, уравнение не имеет корней, так как не существует дискриминанта:
3x2 — x + 7 = 0
D = (-1)2 — 4 • 3 • 7 = -8
Проверить правильность решения можно с помощью калькулятора решения квадратного уравнения.
Решение квадратных уравнений путем разложения на множители
Если известны оба корня квадратного уравнения, его можно разложить по формуле:
ax2 + bx + c = a(x — x1)(x — x2)
Приведенные и неприведенные квадратные уравнения
- Приведенное квадратное уравнение – это квадратное уравнение, где старший коэффициент равен единице.

Например: x2 — 2x + 6 = 0; x2 — x — 1/4 = 0. В каждом из них старший коэффициент равен единице, значит уравнение называется приведенным. - Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Например: 2x2 − 4x — 12 = 0. Первый коэффициент отличен от единицы, значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент. При этом у преобразованного уравнения будут те же корни, что и у первоначального.
Полные и неполные квадратные уравнения
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Если a = 0, то уравнение будет иметь вид линейного: bx + c = 0.
- Если b = 0, то квадратное уравнение принимает вид ax2 + c = 0.
- Если c = 0, то квадратное уравнение принимает вид ax2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение принимает вид ax2 = 0.
Уравнение ax2 = 0 выполняется в том случае, если один из множителей равен нулю.
- Если a ≠ 0, тогда x2 = 0, следовательно x=0;
- Если a = 0, тогда x2 — любое число.
Пример: 6x2 = 0.
Решение: 6x2 = 0, x2 = 0, x = √0, x = 0
Для решения квадратного уравнения такого вида нужно перенести c в правую часть: ax2 = — c, а затем
разделить обе части на a: x2 = — c/а.
- если (— c/а) < 0, то уравнение x2 = — c/а не имеет корней, так как квадрат любого числа всегда равен неотрицательному числу;
- если (— c/а) > 0, то уравнение имеет два корня x = √-c/a и x = -√-c/a.
Пример 1. 8x2 + 32 = 0.
Решение: 8x2 = — 32, x2 = — 4. В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Пример 2. 8x2 — 32 = 0.
Решение: 8x2 = 32, x2 = 4. Ответ: x1=2, x2=-2.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Для этого вынесем за скобки общий множитель x. Получим: x * (ax + b) = 0.
Это уравнение равносильно совокупности двух уравнений:
- x = 0, корень которого равен x = 0;
- ax + b = 0, линейное уравнение, корень которого равен: x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня.
Пример. 0,5×2 + 0,125x = 0
Решение: х(0,5x + 0,125) = 0. Получаем два уравнения:
1) x = 0
2) 0,5x + 0,125 = 0; 0,5x = 0,125; x = 0,125/0,5; x = 0,25.
Значит корни исходного уравнения — 0 и 0,25.
Если вам показалось очень сложным решение квадратных уравнений, то возможно нужно повторить правила и свойства решения простых уравнений.
Для решения уравнений вам также могут понадобится темы: раскрытие скобок и порядок действий в примерах.
Решение квадратного уравнения с помощью Python — Оптимизация
В этой статье мы обсудим, как решить квадратное уравнение с помощью Python.
СОДЕРЖАНИЕ
- ВВЕДЕНИЕ
- Квадратичная формула
- Решение квадратичное уравнение
- Рассчитайте дискриминанту
- Решение для x Значения
- Соли.
 Питон
Питон- Получите пользовательский ввод для коэффициентов уравнения
- Рассчитайте дискриминанту с использованием Python
- Найти корни квадратичного уравнения с использованием Python
- График Квадратичный функция с использованием Python
- Программа для решения квадратичных уравнений Python
41444444444444444444444444414400444004 400444004 4004 40011111111. Программа для решения квадратичных уравнений.
В алгебре квадратные уравнения широко используются во многих задачах. Квадратное уравнение (многочлен второй степени) всегда имеет квадратный член, который отличает его от наших обычных линейных уравнений.
В этом уроке мы будем использовать библиотеку math (предустановленную на Python) для решения квадратных уравнений с помощью Python с помощью Python.
Если он у вас не установлен, откройте «Командную строку» (в Windows) и установите его, используя следующий код:
пип установить numpy pip установить matplotlib
Квадратичная формула 92 – 4 \times 1 \times (-14) = 81$$
Поскольку \(D > 0\), это уравнение будет иметь два корня.
Вычислим \(x_1\) и \(x_2\):
$$x_1 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-5) + \sqrt {81}}{2 \times 1} = 7$$
$$x_2 = \frac{-b + \sqrt{D}}{2a} = \frac{-(-5) – \sqrt{81} }{2 \times 1} = -2$$
Решение этого уравнения: \(x_1 = 7\) и \(x_2 = -2\)
Решить квадратное уравнение с помощью Python
В качестве примера рассмотрим следующее квадратное уравнение:
$$x_1 – 5x_2 – 14 = 0$$
где \(a = 1\) , \(b = -5\) и \(c = -14\) .
Шаг 1: Получите пользовательский ввод для коэффициентов уравнения (a , b, c)
Во-первых, нам нужно получить эти коэффициенты, введенные пользователем:
a, b, c = eval(input("Пожалуйста, введите коэффициенты a, b, c вашего квадратного уравнения: "))
Здесь нам нужно будет передать три значения, разделенных запятыми, как: 1,-5,-14 .
Понятно, что если вы передадите что-то, кроме действительного числа (строкового или логического), это не нарушит функцию ввода, но дальнейшие вычисления работать не будут.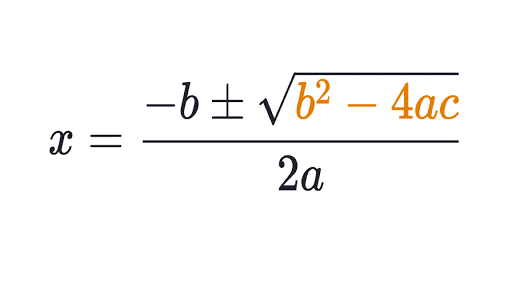 Чтобы предотвратить это, вам следует подумать о добавлении набора проверок для проверки ввода пользователя:
Чтобы предотвратить это, вам следует подумать о добавлении набора проверок для проверки ввода пользователя:
.
check_input = Истина
в то время как check_input:
a, b, c = eval(input("Пожалуйста, введите коэффициенты a, b, c вашего квадратного уравнения: "))
пытаться:
поплавок (а), поплавок (б), поплавок (с)
check_input = Ложь
кроме ValueError:
print("Пожалуйста, убедитесь, что коэффициенты являются действительными числами, и повторите попытку")
check_input = Истина
До сих пор мы создали переменные a , b и c в Python.
Шаг 2: Вычисление дискриминанта с помощью Python
Далее мы вычислим дискриминант. Нам понадобится библиотека math (предустановленная на Python) для использования функции извлечения квадратного корня:
из математического импорта sqrt диск = b*b-4*a*c
Для значений, которые мы ввели выше, значение дискриминанта должно быть 81.
Шаг 3: Найдите корни квадратного уравнения с помощью Python
И, наконец, мы находим корни уравнения. Напомним, что нам также нужно проверить, если дискриминант меньше нуля, то квадратное уравнение не имеет решений:
если диск >=0:
x1 = (-b+sqrt(диск))/(2*a)
x2 = (-b-sqrt(диск))/(2*a)
print("Корни уравнения:", x1, x2)
еще:
print("Уравнение не имеет решений")
Для нашего примера мы должны получить \(x_1 = 7\) и \(x_2 = -2\).
График квадратичной функции с использованием Python
Графическое представление квадратного уравнения – парабола.
Когда квадратное уравнение упрощается до нуля, корнями уравнения являются точки пересечения оси Y.
Давайте построим квадратное уравнение из предыдущего раздела с помощью Python и посмотрим, где расположены корни уравнения.
Начнем с импорта необходимых библиотек:
импортировать matplotlib.pyplot как plt импортировать numpy как np
Далее давайте определим диапазон оси \(x\), который мы хотели бы рассмотреть. Для этого примера возьмем диапазон от -10 до 15:9.0003
Для этого примера возьмем диапазон от -10 до 15:9.0003
х = np.linspace (-10, 15)
И мы можем получить нашу функцию для \(y\), используя параметры из предыдущего раздела:
у = х**2 - 5*х - 14
Сначала мы нанесем оси X и Y в виде пунктирных линий вместе с метками осей:
plt.hlines(y=0, xmin=min(x), xmax=max(x), linestyles='пунктир')
plt.vlines(x=0, ymin=min(y), ymax=max(y), linestyles='штрих')
plt.xlabel('x')
plt.ylabel('у')
Затем постройте параболу:
plt.plot(x, y) plt.show()
И вы должны получить:
На графике выше вы можете видеть, что точки (-2, 0) и (7, 0) являются точками пересечения оси x, которые также являются корнями квадратного уравнения.
Программа для решения квадратных уравнений с использованием Python
из математического импорта sqrt
check_input = Истина
в то время как check_input:
a, b, c = eval(input("Пожалуйста, введите коэффициенты a, b, c вашего квадратного уравнения: "))
пытаться:
поплавок (а), поплавок (б), поплавок (с)
check_input = Ложь
кроме ValueError:
print("Пожалуйста, убедитесь, что коэффициенты являются действительными числами, и повторите попытку")
check_input = Истина
диск = b*b-4*a*c
если диск >= 0:
x1 = (-b+sqrt(диск))/(2*a)
x2 = (-b-sqrt(диск))/(2*a)
print("Корни уравнения:", x1, x2)
еще:
print("Уравнение не имеет решений")
Заключение
В этой статье мы рассмотрели, как решить квадратное уравнение с помощью библиотеки Python и math .
Не стесняйтесь оставлять комментарии ниже, если у вас есть какие-либо вопросы или предложения по некоторым изменениям, и ознакомьтесь с другими моими статьями по оптимизации.
Умножение X в квадратном уравнении — дельта всегда меньше 0
Вопрос задан
Изменено 5 лет, 3 месяца назад 92 $$
$\endgroup$
$\begingroup$
Дискриминант $\Delta$ бывает трех видов.
- $\Delta > 0$: два действительных корня
- $\Delta = 0$: вырожденный (повторяющийся корень)
- $\Delta < 0$: корни комплексно сопряжены $(x\pm iy)$
Вот график рассматриваемой функции:
Этот сюжет имеет два различных реальных корня. Следовательно, $\Delta > 0$. 92-4ac=(121)-(-840)=+961$ (поскольку минус минус это плюс).
92-4ac=(121)-(-840)=+961$ (поскольку минус минус это плюс).
Теперь будут случаи, когда ваш дескриминант отрицательный, это означает, что «настоящих решений нет», о «ненастоящих решениях» вы узнаете позже, но случай с отрицательным дескриминантом легко изобразить графически. Думайте о решении квадратного уравнения как о поиске пересечения параболой оси x (нахождение корней параболы), будут параболы, которые никогда не пересекают ось x, это случаи, когда дескриминант отрицательный.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
решить квадратное уравнение с помощью Python
Эта статья была впервые опубликована на PyShark и любезно предоставлена питон-блогерам. (Вы можете сообщить о проблеме с контентом на этой странице здесь)
Хотите поделиться своим контентом с питон-блогерами? кликните сюда.
В этой статье мы обсудим, как решить квадратное уравнение с помощью Python.
Содержание
- Введение
- Квадратная формула
- Решение квадратного уравнения с помощью Python
- Полный код
- Заключение
Введение
В алгебре квадратные уравнения широко используются во многих задачах. Квадратное уравнение (многочлен второй степени) всегда имеет квадратный член, который отличает его от наших обычных линейных уравнений.
В этом уроке мы будем использовать библиотеку math (предустановленную на Python) для решения квадратных уравнений с использованием Python.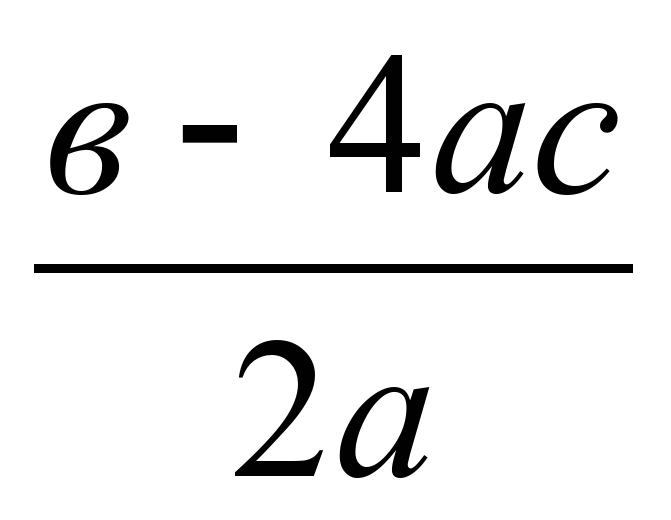
Квадратичная формула
92 – 4ac}}{2a} = \frac{-b \pm D}{2a}$$, что означает, что:
$$x_1 = \frac{-b + D}{2a}$$
$$x_2 = \frac{-b – D}{2a}$$
, и это все шаги, которые нам нужно предпринять, чтобы найти решение квадратного уравнения.
Решение квадратного уравнения с помощью Python
В качестве примера рассмотрим следующее квадратное уравнение: б = -5\) и \(с = -14\) .
Шаг 1: Получите пользовательский ввод для коэффициентов a, b и c
Во-первых, нам нужно получить эти коэффициенты, введенные пользователем:
b, c коэффициенты вашего квадратного уравнения: "))
Здесь нам нужно будет передать три значения, разделенных запятыми, как: 1,-5,-14 .
Понятно, что если вы передадите что-то, кроме действительного числа (строкового или логического), это не нарушит функцию ввода, но дальнейшие вычисления работать не будут. Чтобы предотвратить это, вам следует подумать о добавлении набора проверок для проверки пользовательского ввода:
действительный_вход = Истина
в то время как действительный_вход:
a, b, c = eval(input("Пожалуйста, введите коэффициенты a, b, c вашего квадратного уравнения: "))
пытаться:
поплавок (а), поплавок (б), поплавок (с)
действительный_вход = Ложь
кроме ValueError:
print("Пожалуйста, убедитесь, что коэффициенты являются действительными числами, и повторите попытку")
действительный_вход = Истина
До сих пор мы создали переменные a , b и c в Python.
Шаг 2: вычислить дискриминант
Далее мы вычислим дискриминант. Нам понадобится библиотека math (предустановленная на Python) для использования функции извлечения квадратного корня:
из math import sqrt диск = sqrt(b*b-4*a*c)
Для значений, которые мы ввели выше, значение дискриминанта должно быть 9.
Шаг 3: Найдите корни квадратного уравнения с квадратной формулой, используя Python
И, наконец, мы найдем корни уравнения. Напомним, что нам также нужно проверить, если дискриминант меньше нуля, то квадратное уравнение не имеет решений:
, если диск >=0:
x1 = (-b+диск)/(2*a)
x2 = (-b-диск)/(2*a)
print("Корни уравнения:", x1, x2)
еще:
print("Уравнение не имеет решений")
Для нашего примера мы должны получить \(x_1 = 7\) и \(x_2 = -2\).
Полный код
из математического импорта sqrt
действительный_вход = Истина
в то время как действительный_вход:
a, b, c = eval(input("Пожалуйста, введите коэффициенты a, b, c вашего квадратного уравнения: "))
пытаться:
поплавок (а), поплавок (б), поплавок (с)
действительный_вход = Ложь
кроме ValueError:
print("Пожалуйста, убедитесь, что коэффициенты являются действительными числами, и повторите попытку")
действительный_вход = Истина
диск = sqrt(b*b-4*a*c)
если диск >=0:
x1 = (-b+диск)/(2*a)
x2 = (-b-диск)/(2*a)
print("Корни уравнения:", x1, x2)
еще:
print("Уравнение не имеет решений")
Заключение
В этой статье мы рассмотрели, как решить квадратное уравнение с помощью библиотеки Python и math .

 Для данного действия нужно уметь находить НОК и НОД.
Для данного действия нужно уметь находить НОК и НОД.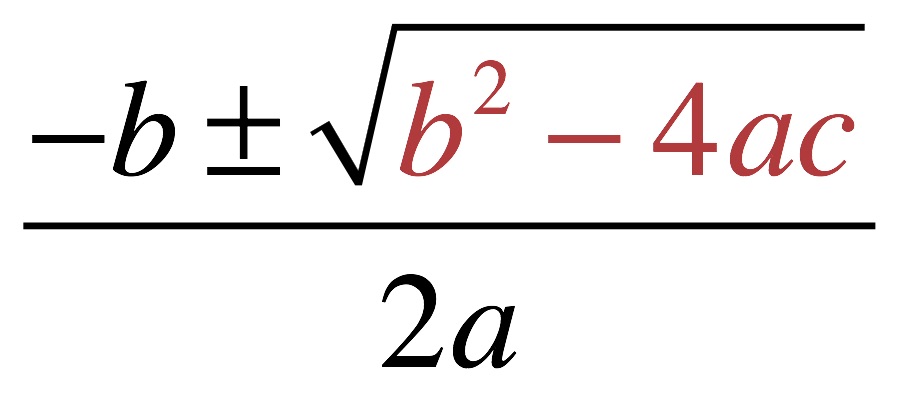
 Питон
Питон