Формулы дискриминантов: Формула дискриминанта — ответ на Uchi.ru

2-(x_0+t)x+x_0t$. То есть на плос­ко­сти парамет­ров ему соот­вет­ствует точка $(p, q)=(-x_0+t, x_0t)$, а при изме­не­нии $t$ такие точки заме­тают прямую.

Оста­лось понять, почему эта прямая каса­ется дис­кри­ми­нант­ной кри­вой. Для этого доста­точно вспом­нить опре­де­ле­ние каса­тель­ной. Наша прямая имеет с дис­кри­ми­нант­ной кри­вой ровно одну общую точку (урав­не­ние имеет только один корень когда $t=x_0$) и при этом прямая не явля­ется вер­ти­каль­ной (т.е. не пере­се­ка­ется с дис­кри­ми­нант­ной кри­вой). А это и озна­чает, что она каса­ется пара­болы $D=0$.

Итак, множе­ство квад­рат­ных урав­не­ний, один корень у кото­рых фик­си­ро­ван, на плос­ко­сти парамет­ров пред­став­ля­ется каса­тель­ной к дис­кри­ми­нант­ной кри­вой. Это наблю­де­ние при­во­дит к заме­ча­тель­ным след­ствиям.

Сколько каса­тель­ных можно про­ве­сти к дис­кри­ми­нант­ной кри­вой — т.е. к обык­но­вен­ной пара­боле — из раз­ных точек плос­ко­сти? Из точек над пара­бо­лой ни одной — у соот­вет­ствующих урав­не­ний нет (действи­тель­ных) кор­ней, а из точек под пара­бо­лой ровно две — по числу кор­ней квад­рат­ного урав­не­ния с положи­тель­ным дис­кри­ми­нан­том.

2$ и корень равен $-p/2$.

Сдвиг пара­болы вдоль оси $Ox$ не меняет ни число кор­ней, ни рас­сто­я­ние между ними (в слу­чае, когда их два). А чему соот­вет­ствуют такие сдвиги на плос­ко­сти парамет­ров?

Если пара­бола каса­ется оси абс­цисс, то корень один и соот­вет­ствующая пара­боле точка плос­ко­сти парамет­ров лежит на дис­кри­ми­нант­ной кри­вой. При «гори­зон­таль­ных» сдвигах пара­болы точка движется по этой кри­вой.

Если пара­бола имеет два пере­се­че­ния с осью $Ox$, то, как мы знаем, точки пере­се­че­ния нахо­дятся из реше­ния квад­рат­ного урав­не­ния. Формула реше­ний квад­рат­ного урав­не­ния $x_{1,2}=(-p\pm \sqrt{D})/2$ под­ска­зы­вают, что рас­сто­я­ние между кор­нями не меня­ется, когда не меня­ется зна­че­ние дис­кри­ми­нанта. Таким обра­зом, гори­зон­таль­ный сдвиг пара­болы соот­вет­ствует движе­нию точки на плос­ко­сти парамет­ров по кри­вой $D=const$. Такие кри­вые — пара­болы, полу­чающейся из дис­кри­ми­нант­ной кри­вой сдвигом по вер­ти­кали.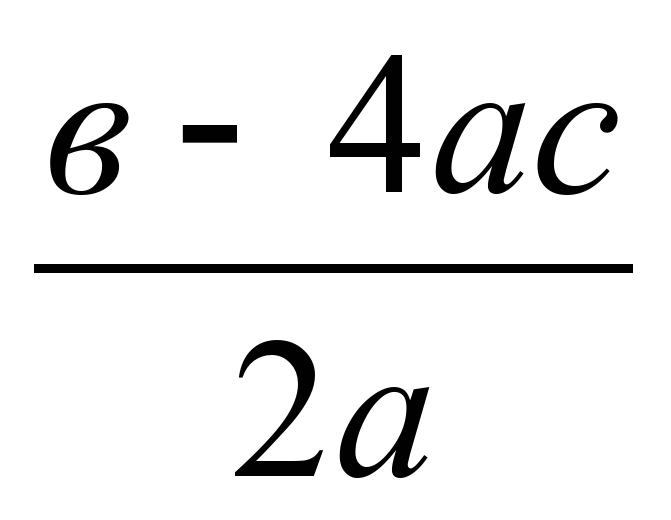

Пре­об­ра­зо­ва­ния плос­ко­сти, при кото­рых все точки двигаются по пара­бо­лам, в неко­то­ром смысле похожи на пово­роты. Только если при обыч­ном пово­роте пере­хо­дит в себя окруж­ность, то при «пара­бо­ли­че­ском пово­роте» — пара­бола (в дан­ном слу­чае, дис­кри­ми­нант­ная кри­вая). Такие пре­об­ра­зо­ва­ния — это часть заме­ча­тель­ной, но мало­из­вест­ной геомет­рии Гали­лея (про неё можно про­чи­тать в брошюре А. В. Хача­ту­ряна «Геомет­рия Гали­лея» или в книге И. М. Яглома «Принцип отно­си­тель­но­сти Гали­лея и неев­кли­дова геомет­рия»).

Кажется самое время пере­смот­реть анимацию, а затем поис­сле­до­вать мир квад­рат­ных урав­не­ний с помощью интер­ак­тив­ной вер­сией ниже. Можно как двигать точку на плос­ко­сти парамет­ров, так и менять зна­че­ния парамет­ров $p$ и $q$.

p =

0,0

q =

0,0

При пере­ходе через дис­кри­ми­нант­ную кри­вую малое непре­рыв­ное изме­не­ние парамет­ров ($p$ и $q$) при­во­дит к суще­ствен­ной пере­стройке изу­ча­емой системы. Подоб­ные объекты и явле­ния изу­чает тео­рия осо­бен­но­стей, кото­рую ещё иногда назы­вают тео­рией ката­строф. И этот сюжет ещё будет про­должен: нас ждёт изу­че­ние дис­кри­ми­нанта для куби­че­ских урав­не­ний и урав­не­ний чет­вёр­той степени. На этом пути мы уви­дим даже кар­тины Саль­ва­дора Дали!

Лите­ра­тура

Васи­льев В. А. Геомет­рия дис­кри­ми­нанта. — М.: МЦНМО, 2017. — (Биб­лио­тека «Матема­ти­че­ское про­свеще­ние»; Вып. 41).

Арнольд В. И. Тео­рия ката­строф. — 3-е изд., доп. — М.: Наука, 1990.

Сгиб­нев А. И. Иссле­до­ва­тельские задачи для начи­нающих. — 2-е изд., испр. и доп. — М.: МЦНМО, 2015.

Другие этюды раздела «Геометрия формул»

  Лестница в бесконечностьОбновлено  Наибольший общий делитель  Геометрическая прогрессия: легенда о шахматах  Убывание геометрической прогрессии

Математические этюды

Калькулятор Дискриминантной Формулы — Mathcracker.Com

Инструкции:

Используйте этот калькулятор для нахождения дискриминанта квадратного уравнения, показывая все шаги. Пожалуйста, введите правильное квадратное уравнение в поле формы ниже.

Дискриминантная формула

Этот калькулятор будет использовать формулу дискриминанта, показывая все шаги для квадратного уравнения, которое вы предоставите.

Вам нужно предоставить действительное квадратное уравнение, например, 2x²+x-1=0, которое уже упрощено, или вы можете предоставить что-то, что является действительным квадратичным выражением, но требует дальнейшего упрощения, например, 2x²+3x-1 = 3/4x — 4/5.

После ввода правильного квадратного уравнения достаточно нажать кнопку «Вычислить», и все шаги вычисления будут предоставлены вам.

Упрощенное квадратное уравнение в форме ax² + bx + c = 0 будет использоваться для вычисления дискриминанта, который сразу укажет на характер корней: Два вещественных корня, один вещественный корень или два комплексных корня. 2 — 4ac\]

Дискриминантное значение

После того, как вы применили приведенную выше формулу и получили значение \(\Delta\) для дискриминанта, каково его значение?

• Шаг 1: Если \(\Delta > 0\): то квадратное уравнение имеет два различных действительных корня
• Шаг 2: Если \(\Delta = 0\): то квадратное уравнение имеет только один действительный корень
• Шаг 3: Если \(\Delta

Что означает два сопряженных комплексных корня ? Графически это просто парабола, которая не пересекает ось x.

С другой стороны, два разных вещественных корня графически означают, что парабола пересекает ось x в двух точках. Дискриминант, равный нулю, означает, что парабола является касательной к оси x.

Зачем заботиться о дискриминанте?

Дискриминант предоставляет вам простую форму для оценки типов корней квадратного уравнения без фактического решения уравнения.

Естественно, мы видим, что дискриминант буквально появляется в квадратичная формула поэтому он явно связан с процессом вычисления квадратичные корни .

2 — 3x — 10 = 0\) имеет два различных действительных корня.

Больше квадратичных калькуляторов

Разбирательство с квадратичные функции и уравнений очень часто встречается в алгебре. Вычисление корней квадратных уравнений тесно связана с вычисление дискриминанта и нахождение вершины .

С геометрической точки зрения, дискриминант указывает на тип расположения параболы, которая представляет квадратичную функцию, и оси x.

Дискриминант — Центр академической поддержки

Что такое дискриминант квадратичной функции и для чего он используется?

Дискриминант квадратичной функции представляет собой значение, определяемое значениями

a, b, и c функции. Это значение скажет нам, сколько решений будет иметь квадратное выражение. Это также позволяет нам выполнить некоторую работу по упрощению квадратичной формулы, прежде чем мы начнем решать.

Наша стандартная формула для квадратичной функции:

y = ax ² + bx + c

Дискриминант равен той части квадратной формулы, которая стоит под радикалом (квадратный корень). Вот общая формула для дискриминанта.

b ² – 4 ac

Интерпретация дискриминанта

Получаем формулу дискриминанта из радикала в квадратичной формуле. Наши правила о квадратных корнях гласят, что у нас не может быть отрицательных чисел под радикалом, если только мы не хотим работать с мнимым числом 9.0005 и

. Нам не нужно будет использовать мнимые числа для нашей работы с дискриминантом.

Значение дискриминанта говорит вам, имеет ли квадратное уравнение 2 решения, 1 решение или нет действительных решений.

·         Если b ² – 4 ac упрощается до положительного числа, то квадратное число имеет 2 решения.

·         Если b ² – 4 ac упрощается до 0, то квадратное уравнение имеет 1 решение.

·         Если b ² – 4 ac упрощается до отрицательного числа, то квадратное уравнение не имеет действительных решений.

Квадратное число, имеющее 2 решения, дважды пересечет ось x .

Квадратное число, имеющее 1 решение, будет касаться своей вершиной оси x .

Квадратное число, не имеющее действительных решений, не пересекает ось x .

Например,

Используйте дискриминант, чтобы определить, сколько решений будет иметь квадратное уравнение. Затем используйте квадратичную формулу, чтобы найти эти решения.

2 x ² + 5 x + 3 = 0

· Шаг 1: Найдите свои значения для A , B, и C

o Наша общая формула для квадратично ax ² + bx + c = 0.

§ Это означает, что a = 2, b = 5 и c = 3

3 90 Убедитесь, что одна сторона уравнения

3 90 равен нулю. Обычно это можно сделать сложением или вычитанием

· Шаг 2: подключите свои значения для A , B и C в формулу дискриминантной и упростите результат

O. Дискриминантная формула B ² — 4 AC

5 ² – 4(2)(3)

25 – 24

1

·         Шаг 3: Интерпретируйте результаты.

o   Если результат положительный, у нас есть 2 действительных решения

o   Если результат равен нулю, у нас есть 1 действительное решение

o   Если результат отрицательный, у нас нет действительных решений (2 мнимых решения)

§  Наш результат равен 1, что является положительным числом. Это означает, что у нас будет 2 решения.

·         Шаг 4: Подставьте значения a, b, и c в квадратную формулу, чтобы найти решения уравнения.

Практические задачи

Используйте дискриминант, чтобы определить, сколько действительных решений будет иметь каждое квадратное уравнение, затем используйте формулу квадратного уравнения, чтобы найти все существующие решения.

1. 5 x ² + 16 x — 84 = 0 2. 3 x ² — 41 x + 110 = 0

3. -2 x ² + 8 x -5 = 0 4. 18 x ² -45 x -50 = 0

0002

5.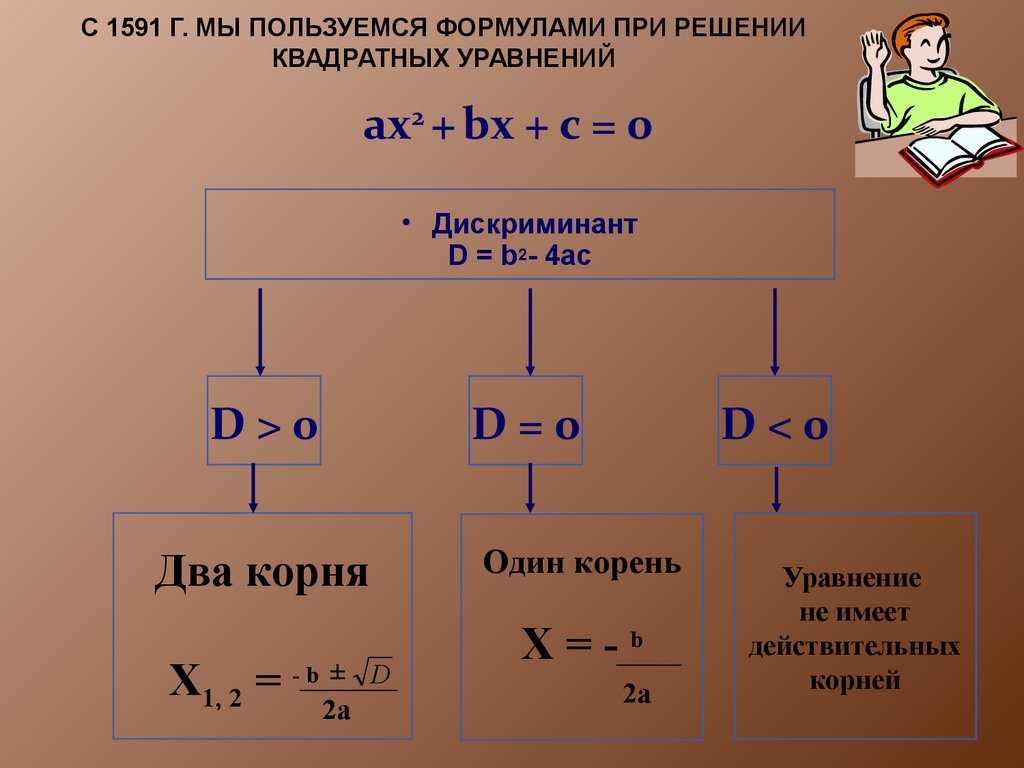 3 x ² -44 x = -96 6. 5 x ² -47 x = 156

раздел математики, занимающийся изучением, изменением и анализом различных математических символов. Это изучение неизвестных величин, которые часто изображаются с помощью переменных в математике. В алгебре есть множество формул и тождеств для изучения ситуаций с переменными. Он также имеет различные подветви, такие как линейная алгебра, продвинутая алгебра, коммутативная алгебра и т. д.

Что такое квадратные уравнения?

Степень многочлена – это наибольшая степень входящей в него переменной. Квадратное уравнение можно определить как полиномиальное уравнение степени 2. 

ax ² + bx + c = 0

, где a и b — коэффициенты, x — неизвестная переменная, а c — константа, а a ≠ 0.

Дискриминантная формула для решения квадратного уравнения

Так как квадратное уравнение имеет степень 2, следовательно, оно будет иметь два решения. Следовательно, будет два значения переменной x, для которых выполняется уравнение. Согласно дискриминантной формуле квадратное уравнение вида ax ² + bx + c = 0 имеет два корня , определяемых как:

,

где D = b ² − 4ac

Знаки ± указывают на два различных решения уравнения. Если дискриминант окажется отрицательным, то данное уравнение не имеет действительных корней.

Вывод формулы дискриминанта

Его можно получить, используя метод квадратов, а затем решив уравнение для x.

топор ² + bx + c = 0

Разделите обе части на a.

⇒ x ² +  = 0

⇒ x ² +  = 

Прибавьте к обеим сторонам.

⇒ x ² +

Применим тождество: a ² + b ² + 2ab = (a + b) ²

квадрат

⇒ 0 02 = 90 с обеих сторон.

⇒ x +  = 

⇒ x = 

⇒ x = 

Примеры вопросов

Вопрос 1. Решите для x: x ² = −2x + 2, используя дискриминантную формулу.

Решение:

Дано: x ² = −2x + 2 или x ² + 2x − 2 = 0

б = 2, с = -2.

⇒ x =

⇒ x =

⇒ x = (−1 + √3), (−1 – √3).

Вопрос 2. Найдите y: 2y ² − 8y − 10 = 0, используя дискриминантную формулу.

Решение:

Дано: 2y ² − 8y − 10 = 0

⇒ y =

⇒ y =

⇒ y = 4, −1.

Вопрос 3. Решите для x: 2x ² − 7x + 3 = 0, используя дискриминантную формулу.

Решение:

Дано: 2x ² − 7x + 3 = 0

Согласно формуле дискриминанта, x =

Здесь a = 2, b = −7, c = 3.

⇒ x =

⇒ x =

⇒ x = 3, 1/2.

Вопрос 4. Найдите x: x ² − 2x + 3 = 0, используя дискриминантную формулу.

Решение:

Дано: x ² − 2x + 3 = 0

⇒ x =

⇒ x =

Так как значение дискриминанта меньше нуля (D = −8 < 0), данное квадратное уравнение не имеет действительного решения.

Вопрос 5. Найдите x: x ² + 5x + 4 = 0, используя дискриминантную формулу.

Решение:

Дано: x ² + 5x + 4 = 0

х =

⇒ х =

⇒ х = -1, -4.

Вопрос 6. Решите для x: 6x ² − x − 15 = 0, используя дискриминантную формулу.

Решение:

Дано: 6x ² − x − 15 = 0

⇒ х =

⇒ х =

⇒ х = 5/3, −3/2.

Вопрос 7.