Формулы математика со степенями: Формулы и свойства степеней

Счет, степени, корни — Математика — Теория, тесты, формулы и задачи

Оглавление:

• Основные теоретические сведения
  • Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений
  • Формулы сокращенного умножения
  • Квадратный трехчлен и теорема Виета
  • Основные свойства степеней
  • Основные свойства математических корней
  • Основные свойства квадратного корня

 

Некоторые рекомендации к проведению алгебраических вычислений, преобразований и упрощений

К оглавлению…

При выполнении численных вычислений с большим количеством операций и дробей желательно выполнять следующие рекомендации:

• Переводите десятичные дроби в обыкновенные, т.е. такие у которых есть числитель и знаменатель.
• Не старайтесь посчитать сразу все выражение. Выполняйте вычисления по одному действию, пошагово. При этом учтите, что:
  • сначала выполняют операции в скобках;
  • затем считают произведения и/или деления;
  • потом суммируют или вычитают;
  • и в последнюю очередь, если это была многоэтажная дробь, делят уже полностью упрощенный числитель на тоже полностью упрощенный знаменатель;
  • причем выполняя в первую очередь операции в скобках также соблюдают ту же последовательность, сначала произведения или деления внутри скобок, потом суммирование или вычитание в скобках, а если внутри скобки есть другая скобка то действия в ней выполняются прежде всего.
• Не спешите умножать и делить «страшные числа». Скорее всего, в одном из следующих действий что-то сократится. Чтобы проще было сократить можно числа раскладывать на простые множители.
• При сложении и вычитании выделяйте в дробях целую часть (если это возможно). При умножении и делении, наоборот, приводите дробь к виду без целой части.

От корней в знаменателе принято избавляться. Для избавления от корня над всем знаменателем умножают числитель и знаменатель на выражение, равное знаменателю. Для избавления от корня над частью знаменателя умножают числитель и знаменатель на сопряженное знаменателю выражение. В этом случае образуется разность квадратов (сопряжённым для (

a — b) является выражение (a + b) и наоборот).

При преобразовании или упрощении алгебраических выражений последовательность действий такова:

• Разложить на множители все, что можно разложить на множители.
• Сократить все, что можно сократить.
• И только потом приводить к общему знаменателю. Ни в коем случае не пытайтесь сразу сломя голову приводить к общему знаменателю. Пример будет становиться чем дальше, тем страшнее.
• Снова разложить на множители и сократить.

Для того чтобы перевести десятичную периодическую дробь в обыкновенную

(с числителем и знаменателем) необходимо:

• Из числа, стоящего до второго периода в исходной периодической дроби вычесть число, стоящее до первого периода в этой же дроби и записать полученную разность в числитель будущей обыкновенной дроби.
• В знаменателе же записать столько девяток, сколько цифр в периоде исходной дроби, и столько нулей, сколько цифр между запятой и первым периодом.
• Не забыть про целую часть, если она есть.

При решении задач из данной темы также необходимо помнить много сведений из предыдущих тем. Приведём далее основные из них.

 

Формулы сокращенного умножения

К оглавлению…

При выполнении различных алгебраических преобразований часто удобно пользоваться формулами сокращенного умножения. Зачастую эти формулы применяются не столько для того чтобы сократить процесс умножения, а наоборот скорее для того, чтобы по результату понять, что его можно представить как произведение некоторых множителей. Таким образом, данные формулы нужно уметь применять не только слева направо, но и справа налево. Перечислим основные формулы сокращенного умножения:

Последние две формулы также часто удобно использовать в виде:

 

Квадратный трехчлен и теорема Виета

К оглавлению…

В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то

разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т. е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения согласно теореме Виета может быть вычислено по формуле:

Итак, еще раз о теореме Виета:

• Если D < 0 (дискриминант отрицателен), то уравнение корней не имеет и теорему Виета применять нельзя.
• Если D > 0 (дискриминант положителен), то уравнение имеет два корня и теорема Виета прекрасно работает.
• Если D = 0, то уравнение имеет единственный корень, для которого бессмысленно вводить понятие суммы или произведения корней, поэтому теорему Виета тоже не применяем.

 

Основные свойства степеней

К оглавлению…

У математических степеней есть несколько важных свойств, перечислим их:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень. Ну а основное свойство отрицательной степени записывается следующим образом:

 

Основные свойства математических корней

К оглавлению…

Математический корень можно представить в виде обычной степени, а затем пользоваться всеми свойствами степеней приведёнными выше. Для представления математического корня в виде степени используют следующую формулу:

Тем не менее можно отдельно выписать ряд свойств математических корней, которые основываются на свойствах степеней описанных выше:

Для арифметических корней выполняется следующее свойство (которое одновременно можно считать определением корня):

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство (из под корня нечетной степени можно выносить знак «минус»):

Так как значение корня четной степени может быть только неотрицательным, то для таких корней имеется следующее важное свойство:

Итак всегда нужно помнить, что под корнем четной степени может стоять только неотрицательное выражение, и сам корень тоже есть неотрицательное выражение.  Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:

 

Основные свойства квадратного корня

К оглавлению…

Квадратным корнем называется математический корень второй степени:

Квадратный корень можно извлечь только из неотрицательного числа. При этом значение квадратного корня также всегда неотрицательно:

Для квадратного корня существует два важных свойства, которые важно очень хорошо запомнить и не путать:

Если под корнем стоит несколько множителей, то корень можно извлекать из каждого из них по-отдельности. При этом важно понимать, что каждый из этих множителей по-отдельности (а не только их произведение) должны быть неотрицательными:

какие операции можно выполнять с разными основаниями, примеры

Содержание:

• Что такое степень — определение, какие существуют виды
• Свойства степени с натуральным показателем
• Степень с целым и дробным показателем
• Какие возможны действия со степенями, формулы
  • Основные действия со степенями
• Примеры задач с решением

Содержание

• Что такое степень — определение, какие существуют виды
• Свойства степени с натуральным показателем
• Степень с целым и дробным показателем
• Какие возможны действия со степенями, формулы
  • Основные действия со степенями
• Примеры задач с решением

Что такое степень — определение, какие существуют виды

Для \(а\;\in\;R,\;n\;\in\;N:\) 

а в степени n равняется а, перемноженному на себя n раз; а называют основанием степени, n — показателем. {-1}.\)

Ответ: n = -1.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Экспоненты и формулы степеней — Законы экспонентов Формулы и решенные примеры

Если вы снова и снова задаетесь вопросом, что такое экспонента в математике, то знайте, что экспонента, также известная как степень, представляет собой математический способ выражения числа, умноженного на себя определенное определенное число раз. С математической точки зрения, когда мы записываем нецелое число а, на самом деле это ¹ , обозначаемое как а — в степени 1.0004 = а*а*а

а ⁴ = а*а*а*а

а ⁵ = а*а*а*а

:

:

а ^п = а* а*а*а*а*а*а. . . n раз.

Ниже приведена стандартная формула экспоненты и степени для решения задач на экспоненты.

(am)n = (an)m = a(mn)

Данная диаграмма разбивает части экспоненциального выражения, точно определяя, какое число является экспоненциальной степенью фактора.

Что такое сила в математике?

В математике мощность определяется как выражение, представляющее многократное умножение одного и того же заданного числа. Записывается как «возведение числа в степень любого другого числа».

Например, 7 × 7 × 7 × 7 = 2041, что также может быть записано как 7 ⁴ = 2041, что означает, что число «7» нужно умножить четыре раза само на себя, чтобы получить число «2041». . Другими словами, можно сказать, что число «4», возведенное в степень 4, или число «7», возведенное в степень 4 9.0003-я -я сила», что дает нам число «7». Здесь число «4» называется основанием, а «4» — степенью или показателем степени.

Что такое экспонента в математике?

Показатель степени в математике определяется как положительное или отрицательное число, которое описывает степень, в которую возводится основание числа.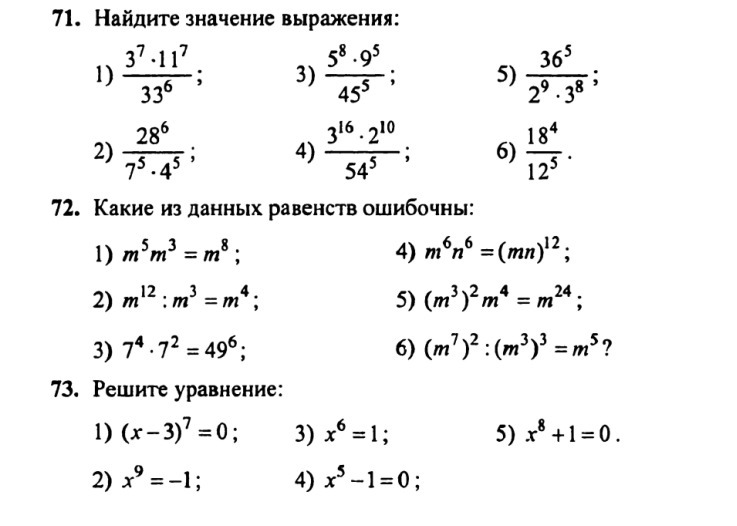 Другими словами, он указывает, сколько раз нужно использовать число в процессе умножения.

 Например, 6 ³ = 6 × 6 × 6 равно 216. Где базовое число равно «6», которое используется 3 раза при умножении. Следовательно, мы умножаем число «6» три раза само на себя, чтобы получить число «216». В геометрии куб и квадрат являются двумя наиболее часто используемыми показателями степени.

Табличное представление Уточняющие определения

Выражения	90 002 Выражение длинной руки	Основание	Экспонента/мощность	Значение
2 5	2×2×2×2×2	2	5	9 0002 32
5 3	5×5×5	5	90 002 3	125
3 5	3×3 ×3×3×3	3	5	243
7 4	7×7×7×7	7	4	2401

В задачах на чтение Математические выражения с экспоненциальными степенями, такие как74, часто произносятся как «семь в четвертой степени». Опять же, экспоненциальные выражения, такие как 74, часто читаются как «4-я степень 7».

(изображение будет загружено в ближайшее время)

Законы экспоненты Формулы

Существуют различные законы экспоненты, которые вы должны практиковать и помнить, чтобы полностью понять экспоненциальные понятия. Следующий экспоненциальный закон подробно описан с примерами экспоненциальных степеней, радикалов и корней. 9n}\]

\[a\sqrt{c}+b\sqrt{c}\] = \[(a+b)\sqrt{c}\]

\[\sqrt{a}+\sqrt {b}\] ≠ \[\sqrt{(a+b)}\]

\[\frac{ax}{y}=\sqrt[y]{ax}\]

Свойства экспонент и радикалов

Экспонента и радикальные правила	Пример	Примечания 900 05
xᵐ=x⋅x⋅x⋅x…..(m раз)	2³=2⋅2⋅2=8	92=\frac{9}{4}\]	Если основание возведено в отрицательную степень, это означает, что нужно взять обратную величину и сделать показатель степени положительным.
\[a\sqrt{x}\times b\sqrt{y}=ab\sqrt{xy}\]	\[2\sqrt{3 }\раз 4\ sqrt{5}=8\sqrt{15}\]	Перемножая два подкоренных члена, вы можете умножить то, что находится снаружи (коэффициент), и то, что внутри (коренное число). Это можно сделать только в том случае, если корни (индексы) такие же, как квадратный корень или кубический корень. 92=16; x=\pm 4\]	Требуется включить в уравнение с четным показателем степени как положительное, так и отрицательное решение при извлечении четного корня. Поскольку и положительный корень, и отрицательный корень работают, когда возводятся в эту степень. Знак квадратного корня дает только положительные решения.

 

Решение экспоненциальных уравнений с использованием законов показательного уравнения, следующее правило поможет вам четко понять различные способы нахождения неизвестного значения в показательном уравнении.

92-x-2=0\]         ……….3

Применяем правила разложения, упрощаем и решим

Получаем

\[(x-2)(x+1)\]

\[x= +2,-1\].

Решенные примеры формул показателей и степеней

Пример 1:

If m ² +n ² +o ² = mn+no+om, упростить [y ^{m 900 04 /г п ] m-n × [y n /y o ] n-o × [y o /y m ] o-m}

Решение1:

Используя m ^a /n ^b = m ^a-b , получаем

→ (y ^m-n ) ^m-n ×(y ^n-o ) ^n-o ×(y ^o-m ) ^o-m

По формуле

(m-n) ² = m ² +n ² -2mn в экспоненте,

9000 2 → у(м²+n²−2мн)×у(м²+ o²−2no)×y(o²+m²−2om)

Математика

m ^a . m ^b =m ^a+b

→ y(m²+n²−2mn+n²+o²−2no+o²+m²−2om)

→ y2(m²+n²+o²−(mn+no+om))

→ y ^{[2(0 )]}

→ y ⁰ =1

 

04 =270

Решение 2:

Сначала вытащим общий термин, с которым мы получаем

→ 3 ^2y-1 (1+3 ² )

Видим, что здесь мы используем формулу для любого нецелого числа a ^m+n = a ^м . a ⁿ при выражении 3 ^2y+1 как произведения 3 ^2y-1 и 3 ² .

→ 3 ^2y-1 (10)=270

→ 3 ^2y-1 =27

→ 3 ^2y-1 =3 ^{3 9000 4}

→ 2y−1=3

→ y = 2.

Формула экспоненты — GeeksforGeeks

Экспонента является одной из важных основ математики. Экспоненты используются в различных формулах, таких как ряды, биномиальное разложение и многие другие. Различные формулы экспоненты используются в различных областях математики. Формулы экспоненты очень просты и полезны. Давайте узнаем о показателях и их формулах. Экспоненты — это степени любой переменной или константы.

Показатели 

Когда любое число или переменная (x) умножается n раз, результатом будет x ⁿ . Тогда n называется показателем степени x. x.x.x.x.x.x … n times = x ⁿ   , тогда x — основание, а n — показатель степени этого основания. Экспонента — это степень числа. Оно умножается само на себя. Экспонента определяет, сколько раз число умножается само на себя. Пример, 2.2.2 = 2 ³ , основание = 2, показатель степени = 3.

Экспоненты Формулы  

Формулы степени
Формула степени произведения n раз	x.x.x.x … n раз = x n
Правило умножения	x m . x n = x (m + n)
Правило деления	x m /x n = x 9 0003 (m – n)
Правило степени произведения	(xy) n = x n . y n
Правило степени дроби	(x/y) n = x n /y n
Правило мощности	[(x) m ] n = x mn
Нулевой показатель	(x) 0 = 1, если x ≠ 0
Одна экспонента	(x) 1 = x
Отрицательная экспонента	x -n = 1/x n 9006 9
Дробная экспонента	x m/n = n √(x) m

Примечание: Если основание уравнения одинаковое, мы можем приравнять показатели.

Примеры вопросов 

Вопрос 1. Решите следующее: 

• 2.2.2.2     
• 3 ² .3 ³  
• 90 619 (4,5) ²   
• (5) ⁰   
• 2 ^-2
• 2 ⁵ /2 ³  
• [(3) ¹ ] ²  9062 0
• 4 ^3/2  
• (4/3) ² 

Решение:

• 2.2.2.2 = 2 ⁴ = 16
• 3 ² ,3 ³ = 3 ^{(2 + 3)} = 3 ⁵ = 243
• (4,5) ² = 4 ² .5 ² = (16) = 1/2 ² = 1/ 4
• 2 ⁵ /2 ³ = 2 ^(5-3) = 2 ² = 4
• [(3) ¹ ] 900 03 2 = 3 ^{(1. 2)} = 3 ² = 9
• 4 ^3/2 = √(4) ³ = √64 = 8
• (4/3) ² = 4 ² /3 ² = 16/9

Вопрос 2: Упростить:

1. (2 ³ ÷ 2 ^{4 9000 4 ) -2 .2 3}      
2. 3 ^{(- 2)} ÷ 4 ²   
3. 3 ³ .4 ² /6 ⁴   
4. (3 ​​ ^-1 + 2 ^-2 + 4 ^-1 )

Решение:

9 0912

(2 ³ ÷ 2 ⁴ ) ^-2 . 2 ³ = (2 ³ /2 ⁴ ) ^-2 .2 ³ = [2 ^{(3 – 4)} ] ^-2 .2 ³ = [2 ^{— 1} ] ^-2 .2 ³ = 2 ^(-1).(-2) .2 ³ = 2 ² . 2 ³ = 2 900 03 5 = 32

3 ^(-2)

÷ 4 ² = 1/(3) ² (4) ² = 1/9,16 = 1/144

3 ³ .4 ² /6 ⁴ = 3 ³ .4 ² /(2.3) ⁴ = 3 ³ .2 ⁴ /2 ^{4 9 0004 .3 4 = 1/3}

( 3 ^-1 + 2 ^-2 + 4 ^-1 ) = (1/3 + 1/2 ² +1/4) = (1/3 + 1/4 + 1/4) = 5/6

Вопрос 3: Найдите значение x, если (4) ^{x + 12} = (4) ^{2x + 6} .(2) ⁶

Решение:  

(4) ^x+12 = (4) ^2x+6 .( 2 ² ) ³

(4) ^x+12 = (4) ^2x+6 .(4) ³

(4) 900 03 х+12 = (4) ^{2х +6+3}

(4) ^x+12 = (4) ^2x+9

Поскольку основания равны, степени приравниваются

x +12 = 2x + 9

2 х – х = 12 – 9

x = 3

Вопрос 4. Найдите значение {343 ^4/3 } ^1/4

Решение: 

{343 ^4/3 } ^1/4   = {(7 ³ ) ^4/3 } ^1/4  

= {7} ^{3.(4/3 ).(1/4)} = 7

Вопрос 5: Найдите значение x + y, если:

(81) ^y = 27/(3) ^x , 4 ^y = 256

Решение:  

(3 ⁴ ) ^y = (3 ³ )/(3) ^x

(3) ^{4 года} = (3) ^3-x

Так как основания равны, то степени приравниваются

4y = 3-x ⇢ Уравнение (1)

4 ^y = 256

4 9 0003 г = (4) ⁴

y = 4

Подставляя значение y в уравнение 1,

4,4 = 3-x

16 = 3-x

x = -13

Теперь нам нужно найти значение x + y

x + y = -13+4 = -9

Вопрос 6: Если ( -9) ^2x+7 = (-9) ^x . 81, затем найдите значение (х ² + 1)/(х ² – 12).

Решение:

(-9) ^2x+7 = (-9) ^x . 81

(-9) ^2x+7 = (-9) ^x . (-9) ²

(-9) ^{2x + 7} = (-9) ^{x + 2}

Поскольку основы равны, тогда мощности приравниваются

2x + 7 = x + 2

2x-x = 2-7 ​​

x = -5

Теперь нам нужно найти значение  (x ² + 1)/(x ² – 12) 

(x ² + 1)/(x ^{2 900 04 – 12 )  = [(-5) 2 + 1]/[(-5) 2 – 12]}

= [25 + 1]/[25 – 12]

= 26/13  

( х ² + 1)/(х ² – 12) = 2

Вопрос 7: Найдите мультипликативную обратную :- [(-13) ^-1 ] ² ÷ (91) ^-1 90 005

Решение:  

Пусть x = [(-13) ^-1 ] ² ÷ (91) ^-1  

x = (-13) ^-2 ÷ (91) ^-1

= (- 1/13 ² ) ÷ (1/91)

= (-1/13 ² ) × 91

x = -7/13

Мультипликативная обратная величина определяется как 1/x, т.

No related posts.