№ 37 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите мне вычислить площади и периметры – Рамблер/класс
№ 37 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. Помогите мне вычислить площади и периметры – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
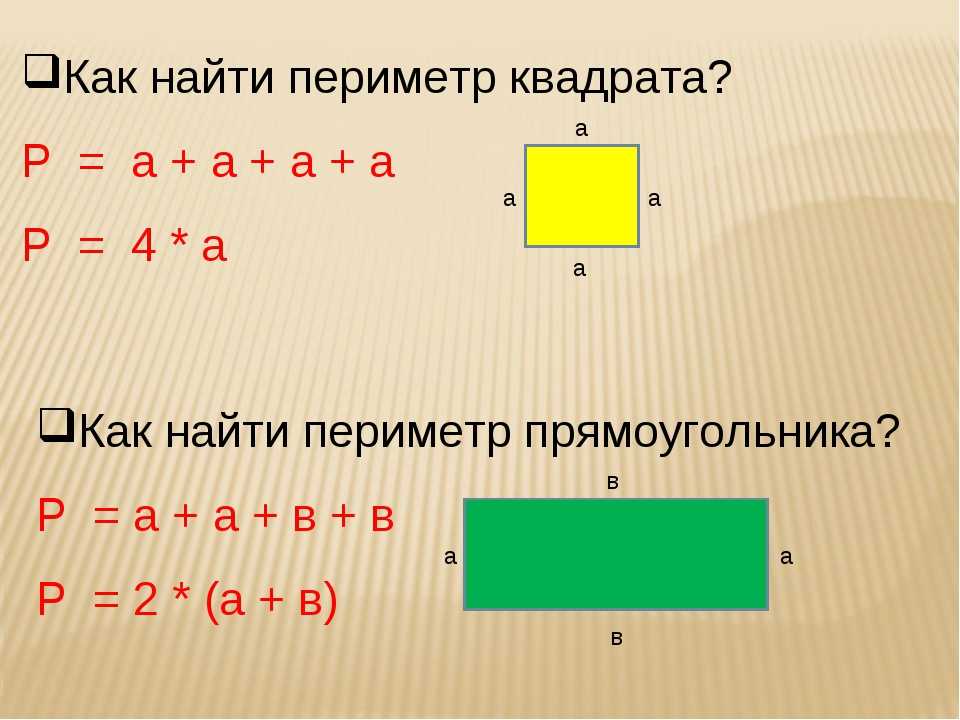
1) Запиши формулы периметра и площади прямоугольника, обозначив его стороны буквами а и b, периметр — буквой Р, a площадь — S.
2) Введи обозначения и запиши формулы периметра и площади квадрата.
3) Из квадрата со стороной 10,6 см вырезали два прямоугольника, как показано на чертеже. Известны длины отрезков АВ = 7,5 см, DE = KF = 5,8 см, EF = 8,6 см. Найди периметр и площадь получившейся фигуры. Округли значение площади с точностью до десятых.
ответы
1) Р = 2(а + b), S = а ∙ b.
2) Пусть сторона квадрата — а, Р = 4а, S= а2
3) АМ = ВС = 10,6 — DE = 10,6 — 5,8 = 4,8 см;
МК = 10,6 — EF = 10,6 — 8,6 = 2 см;
CD = 10,6 — AB = 10,6 — 7,5 = 3,1 см;
Р = АВ + ВС + CD + DE + EF + FK + КМ + МА = 7,5 + 4,8 + 3,1 + 5,8 + 8,6 + 5,8 + 2 + 4,8 = 42,4 см;
S= SABCM + SKDEF = 7,5 ∙ 4,8 + 5,8 ∙ 8,6 = 85,88 см2 ≈ 85,9 см2
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.
Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет.
Всегда ли это можно сделать? Почему?
ГДЗМатематика6 классДорофеев Г. В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
ГДЗЕГЭРусский языкЦыбулько И.П.
Площадь прямоугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь прямоугольника. Для нахождения площади прямоугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Площадь прямоугольника. Определение
Определение 1. Площадь прямоугольника − это величина той части плоскости, которую занимает прямоугольник.
Площадь прямоугольника. Доказательство
Теорема 1. Площадь S прямоугольника со смежными сторонами a и b равна произведению этих сторон :.
Доказательство. Рассмотрим прямоугольник со сторонами a, b и площадью S (Рис.1). Докажем, что .
Достроим прямоугольник до квадрата со стороной a+b (Рис.2). Площадь этого квадрата равна (a+b)·(a+b) (см. статью Площадь квадрата онлайн).
С другой стороны, данный квадрат состоит из двух квадратов со сторонами со сторонами a и b и площадями a2 и b2, соответственно и из двух прямоугольников с площадями S. Поэтому сумма площадей этих двух квадратов и двух прямоугольников равна площади квадрата со стороной a+b:
Упрощая полученное равенство, получим: .
Площадь прямоугольника через стороны
Из вышеизложенной теоремы следует, что площадь прямоугольника через его смежные стороны вычисляется из формулы:
Пример 1. Стороны прямоугольника равны и . Найти площадь прямоугольника.
Решение. Для нахождения площади прямоугольника воспользуемся формулой (1).
Подставим , в (1):
Ответ:
Площадь прямоугольника через сторону и диагональ
Пример 2. Известна сторона прямоугольника и диагональ (Рис.3). Найти площадь прямоугольника.
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления площади прямоугольника через диагональ и сторону:
Подставим , в (3):
Ответ:
Площадь прямоугольника через периметр и сторону
Пример 3. Известны сторона прямоугольника и периметр (Рис.4). Найти площадь прямоугольника.
Решение. Найдем сначала неизвестную сторону прямоугольника. Для этого воспользуемся теоремой Пифагора:
Площадь прямоугольника вычисляется из формулы (1). Подставляя (4) в (1), получим формулу вычисления площади прямоугольника через периметр и сторону:
Подставим , в (5):
Ответ:
Площадь прямоугольника через диагональ и периметр
Пример 4.
2}{\large 8}. \)
Подставляя , в (15), получим:
Ответ:
Смотрите также:
- Прямоугольник. Онлайн калькулятор
Площадь прямоугольника — 3 метода
Содержание
В геометрии площадь плоской двумерной формы — это область, покрываемая ею (область, ограниченная периметром) на двумерной плоскости. Другими словами, мы можем сказать, что площадь любой фигуры — это количество единичных квадратов, которые могут в нее поместиться. Здесь единичный квадрат относится к квадрату со стороной $1$ единицы. Хорошим примером является графическая бумага. Подсчитав количество квадратов в регионе, вы можете найти площадь этого региона.
Прямоугольник — 2D-плоскость Рис. 9{2}$.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
{2}$ или $12 кв см$. 9{2}$.
Как вычислить площадь прямоугольника по сторонам?
Площадь прямоугольника равна произведению его длины на ширину. Для нахождения площади прямоугольника используются следующие шаги:
Шаг 1: Запишите длину и ширину прямоугольника
Шаг 2: Преобразование длины и ширины в одни и те же единицы, если единицы длины и ширины не совпадают
Шаг 3: Подставить значения длины и ширины прямоугольника в формулу 9{2}$.
Пример 2: Найдите площадь прямоугольника, длина которого 1,5 м$, а ширина 60 см$.
Длина прямоугольника $l = 1,5 м$Ширина прямоугольника $w = 60 см$
Обратите внимание, что длина и ширина имеют разные единицы измерения. Итак, вам нужно преобразовать либо $m$ в $cm$, либо $cm$ в $m$.
Преобразуем ширину в $m$.
Ширина $w = 60 см = \frac {60}{100} = 0,60 м$.
Площадь прямоугольника $A = l \times w$
9{2}$ Необходимое количество каменных плит = $\frac {\text{Площадь пути}}{\text{Площадь одной каменной плиты}} = \frac {39 000 000}{260} = 150000$.
Формула площади прямоугольника с использованием диагонали
Рассмотрим прямоугольник длины $l$, ширины $w$ и диагонали $d$. 9{2}$. Площадь прямоугольника зависит от его длины и ширины и рассчитывается путем вычисления произведения длины и ширины.
Практические задачи
- Найдите площадь прямоугольника, длина и ширина которого равны
- Длина = 9 долларов США за единицу $ и ширина = 7 долларов США за единицу $
- Длина = 15 мм$ и ширина = 12 мм$
- Длина = 17 долларов США в дюймах и ширина = 8 долларов США за единицу
- Найдите длину прямоугольника, площадь и ширина которого равны
- Площадь = 9 долларов США{2}$ и ширина = 7 долларов см долларов США
- Площадь прямоугольного забора составляет 500 квадратных футов.
Если ширина забора 20 футов, то найдите его длину - Найдите площадь прямоугольника, длина которого в $12 см$, а ширина в $3$ меньше
- Сколько квадратов со стороной $2 см$ занимают поверхность прямоугольника длиной $24$ см и шириной $8 см$?
Если ширина забора 20 футов, то найдите его длинуРекомендуемое чтение
- Что такое длина? (с определением, единицей измерения и преобразованием)
- Вес – определение, единица измерения и преобразование
- Что такое емкость (определение, единицы измерения и примеры)
- Что такое время? (с определением, фактами и примерами)
- Что такое температура? (с определением и единицами измерения)
- Чтение календаря
- Периметр прямоугольника – определение, формула и примеры
- Периметр квадрата – определение, формула и примеры
- Площадь квадрата – определение, формула и примеры 9{2}}$
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34146
- Генри Африк
- Нью-Йоркский городской технологический колледж через Нью-Йоркский технологический колледж в CUNY Academic4 Works 909009
Измерение площади геометрических фигур — один из самых привычных способов использования математики в нашей повседневной жизни.
Площадь здания, высота картины, количество бумаги в рулоне бумажных полотенец — все это примеры предметов, которые часто измеряются в терминах площади. В этой главе мы выведем формулы для площадей изучаемых нами геометрических объектов.Площадь измеряется в квадратных дюймах, квадратных футах, квадратных сантиметрах и т. д. Базовой единицей измерения является единичный квадрат, длина стороны которого равна 1 (рис. \(\PageIndex{1}\)). Его площадь составляет 1 квадратный дюйм, 1 квадратный фут, 1 квадратный сантиметр и т. д., в зависимости от того, какое измерение длины выбрано. Площадь любой замкнутой фигуры определяется как количество содержащихся в ней единичных квадратов.
Пример \(\PageIndex{1}\)
Найдите площадь прямоугольника длины 5 и ширины 3.
Решение
Из диаграммы видно, что площадь равна \((5)(3)=15\)
Ответ: 15.
Отсюда следует следующая теорема:
Теорема \(\PageIndex{1}\)
Площадь прямоугольника равна произведению длины на его ширину.
\(А = lw\)
Пример \(\PageIndex{2}\)
Найдите площадь квадрата со стороной 3.
Решение 92 — 22x — 15} & = & {0} \\ {(9x + 5)(x — 3)} & = & {0} \end{массив}\)
\(\begin{массив} {rcl } {9x + 5} & = & {0} \\ {x} & = & {-\dfrac{5}{9}} \end{массив}\) \(\begin{массив} {rcl} {x — 3} & = & {0} \\ {x} & = & {3} \end{array}\)
Мы отвергаем ответ \(x = -\dfrac{5}{9}\), потому что \ (BC = 2x = 2(-\dfrac{5}{9}) = -\dfrac{10}{9}\) будет иметь отрицательную длину. Поэтому \(х = 3\).
\(AB = 3x — 1 = 3(3) — 1 = 9 — 1 = 8\). \(ВС = 2x = 2(3) = 6\). 92 + 3x — 40} \\ {0} & = & {(x — 5)(x + 8)} \\ {x} & = & {5\ \ \ \ \ \ \ x = -8} \end {массив}\)
Мы отклоняем \(x = -8\), потому что сторона \(BC = x\) прямоугольника будет отрицательной.
Проверка, \(x = 5\):
Ответ: \(x = 5\).
Пример \(\PageIndex{5}\)
Г-образная комната имеет размеры, указанные на схеме. Сколько плиток один на один фут необходимо, чтобы выложить пол плиткой?
Решение
Разделите комнату на два прямоугольника, как показано на рисунке.
\(\begin{array} {rcl} {\text{Площадь комнаты}} & = & {\text{Площадь большого прямоугольника}} \\ {} & + & {\text{Площадь маленького прямоугольника} } \\ {} & = & {(14)(10) + (6)(4)} \\ {} & = & {140 + 24} \\ {} & = & {\text{164 квадратных фута. }} \end{массив}\)
Ответ: 164
Историческая справка
Потребность в измерении площади суши была одной из древних проблем, которая привела к развитию геометрии. И у древних египтян, и у вавилонян были формулы площадей прямоугольников, треугольников и трапеций, но некоторые из их формул были не совсем точными. Формулы этой главы были известны грекам и находятся в «Началах» Евклида.
1 — 14. Найдите площадь и периметр \ (ABCD \):
1.
2.
3.
4.
5.6666
5.
6. .
7.
8.
9.
10.
11.
12.
13.
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 215 — 18. Найти \(х\):
15.
16.
17.
18.
19.
19. Что такое площадь?
20. Теннисный корт имеет длину 78 футов и ширину 36 футов. Какова площадь?
21 — 24. Сколько плиток по футу необходимо, чтобы выложить плиткой каждую из следующих комнат?
21.
22.
23.
24.
25. Бетонная плита весит 60 фунтов на квадратный фут. Каков общий вес прямоугольной плиты длиной 10 футов и шириной 3 фута?
26. Прямоугольный кусок фанеры имеет длину 8 х 10 футов. Если фанера весит 3 фунта на квадратный фут, каков вес всего куска?
Эта страница под названием 6.
Что вы подразумеваете под площадью прямоугольника?
Вам также может понравиться
Последовательность и серия – типы, различия и формулы
Содержание Что такое последовательность и серия? Сигма-нотация серии General
Читать далее
Как решать линейные уравнения с матрицами (с методом и примерами)
Содержание Как решать линейные уравнения с матрицамиУсловие непротиворечивости
Читать далее
Правило Крамера – определение, формулы и примеры
Содержание Что такое правило Крамера?Формула правила КрамераПравило Крамера 2 x
Читать далее
Площадь здания, высота картины, количество бумаги в рулоне бумажных полотенец — все это примеры предметов, которые часто измеряются в терминах площади. В этой главе мы выведем формулы для площадей изучаемых нами геометрических объектов.
