Формулы площади треугольника прямоугольного: Составить алгоритм площади прямоугольного треугольника если известна гипотенуза и катет

Все формулы площади треугольника — найти онлайн с помощью калькулятора

{S = \dfrac{1}{2} \cdot a \cdot h}

Найти площадь

треугольникапрямоугольного треугольникаравнобедренного треугольникаравностороннего треугольника

Известные данные

через основание и высотучерез две стороны и угол между нимичерез сторону и два прилежащих углачерез радиус описанной окружности и 3 сторонычерез радиус вписанной окружности и 3 стороныпо формуле Герона

Сторона a

ммсмдммкмдюймы (in)футы (ft)

Высота h

ммсмдммкмдюймы (in)футы (ft)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Задача нахождения площади треугольника довольно распространена не только в науке, но и в быту. Для вас мы разработали калькулятор для нахождения площади любого треугольника — равнобедренного, равностороннего, прямоугольного или обыкновенного (разностороннего) по 22 формулам.

1. Калькулятор площади треугольника
2. Площадь треугольника
   1. через основание и высоту
   2. через две стороны и угол между ними
   3. через сторону и два прилежащих угла
   4. через радиус описанной окружности и 3 стороны
   5. через радиус вписанной окружности и 3 стороны
   6. по формуле Герона
3. Площадь прямоугольного треугольника
   1. через катеты
   2. через гипотенузу и прилежащий угол
   3. через катет и прилежащий угол
   4. через радиус вписанной окружности и гипотенузу
   5. через вписанную окружность
   6. по формуле Герона
   7. через катет и гипотенузу
4. Площадь равнобедренного треугольника
   1. через основание и сторону
   2. через основание, боковую сторону и угол
   3. через основание и высоту
   4. через боковые стороны и угол между ними
   5. через основание и угол между боковыми сторонами
5. Площадь равностороннего треугольника
   1. через сторону
   2. через высоту
   3. через радиус описанной окружности
   4. через радиус вписанной окружности
6. Примеры задач

Площадь треугольника

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

2}{2} \cdot \dfrac{\sin{(\alpha)} \cdot \sin{(\beta)}}{sin{(\gamma)}}} {\gamma = 180 — (\alpha + \beta)}

a — сторона треугольника

α и β — прилежащие к стороне a углы

Площадь треугольника через радиус описанной окружности и 3 стороны

{S = \dfrac{a \cdot b \cdot c}{4 \cdot R}}

a, b и c — стороны треугольника

R — радиус описанной окружности

Площадь треугольника через радиус вписанной окружности и 3 стороны

{S = r \cdot \dfrac{a + b + c}{2}}

a, b и c — стороны треугольника

r — радиус вписанной окружности

Площадь треугольника по формуле Герона

{S = \sqrt{p \cdot (p-a) \cdot (p-b) \cdot (p-c)}} {p= \dfrac{a+b+c}{2}}

a, b и c — стороны треугольника

p — полупериметр треугольника

Площадь прямоугольного треугольника

Прямоугольный треугольник — это треугольник, в котором один угол прямой (равен 90 градусов).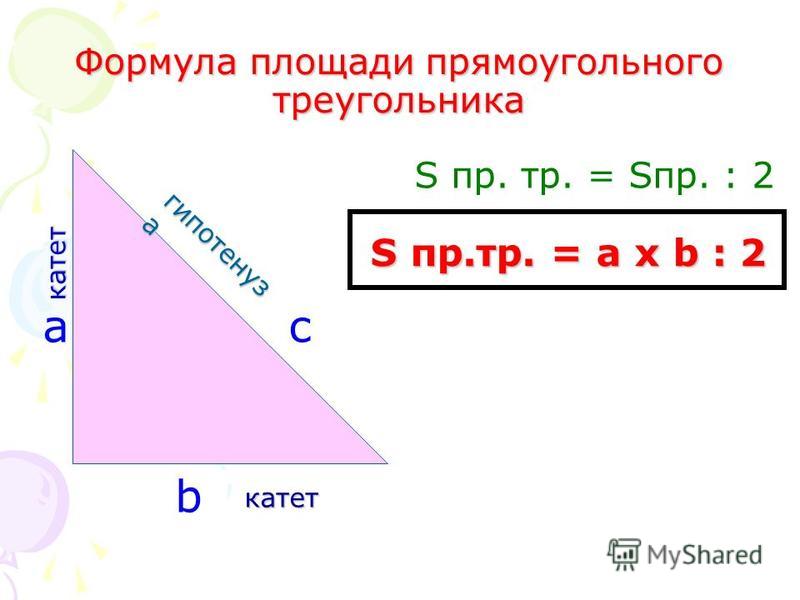 2 \cdot \tg{(\alpha)}}

a — катет прямоугольного треугольника

α — прилежащий к катету a угол

Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу

{S = r \cdot (r+c)}

r — радиус вписанной окружности

c — гипотенуза прямоугольного треугольника

Площадь прямоугольного треугольника через вписанную окружность

{S = c_1 \cdot c_2}

с₁ и с₂ — отрезки, полученные делением гипотенузы точкой касания окружности

Площадь прямоугольного треугольника по формуле Герона

{S = (p-a) \cdot (p-b)} {p= \dfrac{a+b+c}{2}}

a, b и

c — стороны треугольника

p — полупериметр треугольника

Площадь прямоугольного треугольника через катет и гипотенузу

{S = \dfrac{1}{2} \cdot a \cdot \sqrt{c^2 — a^2}}

a — катет прямоугольного треугольника

c — гипотенуза прямоугольного треугольника

Площадь равнобедренного треугольника

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. 2

Проверка .

Как найти площадь треугольника с прямым углом. Как находить площадь треугольника (формулы)

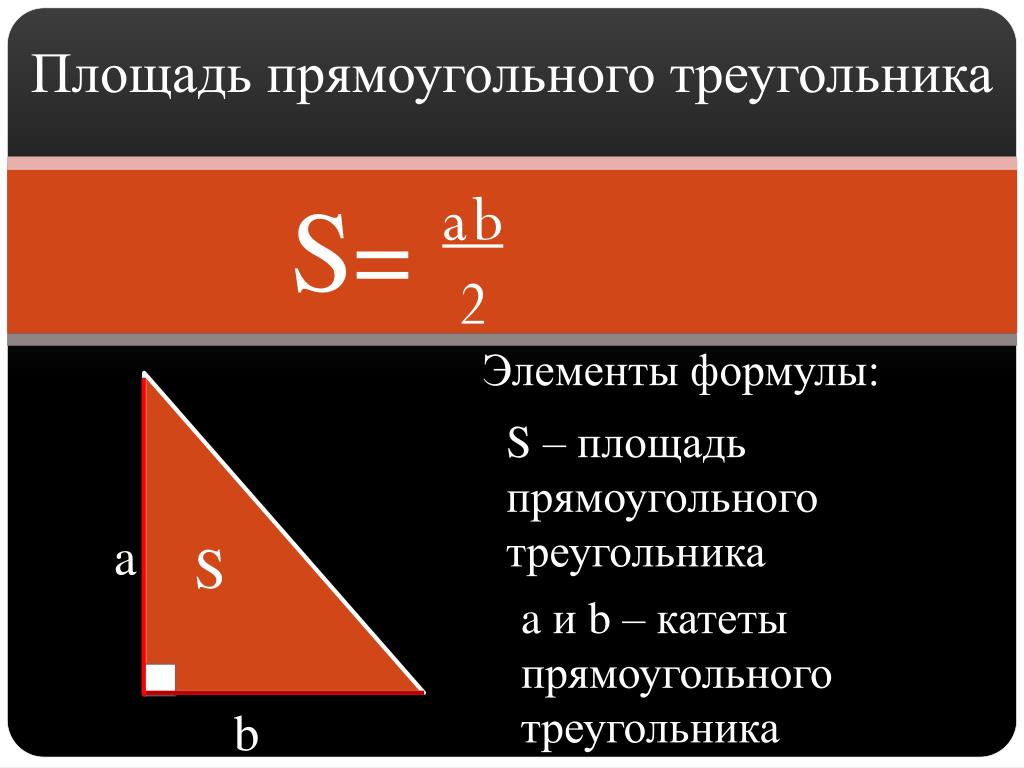
Прямоугольным треугольником называется треугольник, у которого один из углов равняется 90°. Его площадь можно найти, если известны два катета. Можно, конечно, пойти и длинным путем – найти гипотенузу и просчитать площадь по , но в большинстве случаев это только займет лишнее время. Именно поэтому формула площади прямоугольного треугольника выглядит так:

Площадь прямоугольного треугольника равняется половине произведения катетов.

Пример расчета площади прямоугольного треугольника.
Дан прямоугольный треугольник с катетами a = 8 см, b = 6 см.
Вычисляем площадь:
Площадь равна: 24 см 2

Также в прямоугольном треугольнике применяется теорема Пифагора. – сумма квадратов двух катетов равняется квадрату гипотенузы.
Формула площади равнобедренного прямоугольного треугольника вычисляется также как и обычного прямоугольного треугольника.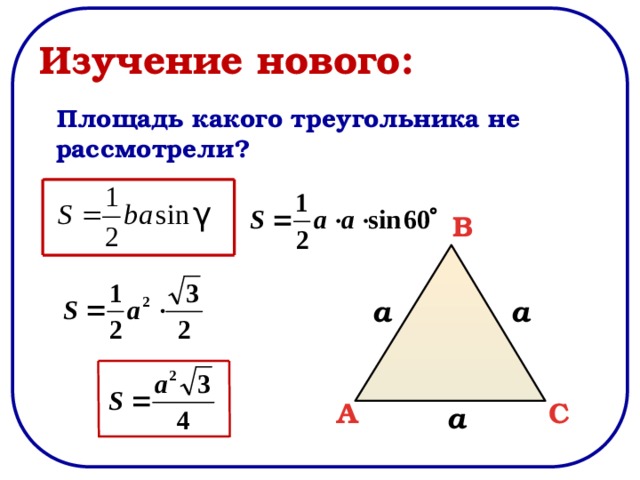

Пример расчета площади равнобедренного прямоугольного треугольника:
Дан треугольник с катетами a = 4 см, b = 4 см. Вычисляем площадь:
Вычисляем площадь:=8 см 2

Формула площади прямоугольного треугольника по гипотенузе может использоваться, если в условии дан один катет. Из теоремы Пифагора находим длину неизвестного катета. К примеру, дана гипотенуза c и катет a , катет b будет равен:
Далее вычисляем площадь по обычной формуле. Пример расчета формулы площади прямоугольного треугольника по гипотенузе идентичен описанному выше.

Рассмотрим интересную задачу, которая поможет закрепить знания формул для решения треугольника.
Задача : площадь прямоугольного треугольника равняется 180 кв. см. найдите меньший катет треугольника, если он меньше второго на 31 см.
Решение : обозначим катеты a и b . Теперь подставим данные в формулу площади:, еще мы знаем, что один катет меньше другого a – b = 31 см
Из первого условия получаем, что
Подставляем данное условие во второе уравнение:

Так как мы находили стороны, то знак минус убираем. 2) высчитываем длину неизвестного катета, затем используем ее для расчета площади треугольника.

Если дана длина одного катета и градусный наклон угла противолежащего ему: находим длину второго катета по формуле — a=b*ctg(C).

Дано: длина одного катета и градусный наклон угла прилежащего к нему: для нахождения длины второго катета применяем формулу — a=b*tg(C).

И последнее, дано: угол и длина гипотенузы: вычисляем длину обеих его катетов, по таким формулам — b=c*sin(C) и a=c*cos(C).

Как находить площадь равнобедренного треугольника

Площадь равнобедренного треугольника можно очень легко и быстро найти по формуле S= b*h / 2, но, при отсутствии одного из показателей, задача значительно усложняется. Ведь необходимо выполнять дополнительные действия.

Возможные варианты задач:

• Дано: длина одной из боковых сторон и длина основания. Находим через теорему Пифагора высоту, то есть длину второго катеты. При условии, что длина основания, разделенная на два, является катетом, а изначально известная боковая сторона – гипотенузой.
• Дано: основание и угол между боковой стороной и основанием. Вычисляем по формуле h=c*ctg(B)/2 высоту (не забываем сторону «c» разделить на два).
• Дано: высота и угол, который был образован основанием и боковой стороной: применяем формулу c=h*tg(B)*2 для нахождения высоты, и полученный результат умножаем на два. Далее вычисляем площадь.
• Известна: длина боковой стороны и угол, который образовался между ним и высотой. Решение: используем формулы — c=a*sin(C)*2 и h=a*cos(C) для нахождения основания и высоты, после чего считаем площадь.

Как найти площадь равнобедренного прямоугольного треугольника

Если все данные известны, то по стандартной формуле S= a* a / 2 вычисляем площадь равнобедренного прямоугольного треугольника, если же в задаче не указаны некоторые показатели, то выполняются дополнительные действия.

Например: нам не известны длины обеих сторон (мы помним, что в равнобедренном прямоугольном треугольнике они равны), но дана длинна гипотенузы. 2, где R — радиус окружности.

Треугольник – плоская геометрическая фигура с одним углом равным 90 °. При этом в геометрии очень часто требуется вычислить площадь такой фигуры. Как это сделать, мы расскажем далее.

Самая простая формула определения площади прямоугольного треугольника

Исходные данные, где: a и b – стороны треугольника, выходящие из прямого угла.

То есть, площадь равна половине произведения двух сторон, которые выходят из прямого угла. Конечно, существует формула Герона, используемая для вычисления площади обычного треугольника, но для определения величины необходимо знать длину трех сторон. Соответственно, вам придется рассчитать гипотенузу, а это лишнее время.

Найти площадь прямоугольного треугольника через формулу Герона

Это всем известная и исходная формула, но для этого вам придется посчитать гипотенузу по двум катетам, используя Теорему Пифагора.

В этой формуле: a, b, c – стороны треугольника, а p – полупериметр.

Найти площадь прямоугольного треугольника по гипотенузе и углу

Если в вашей задаче не известен ни один из катетов, то воспользоваться самым простым способом вы не сможете.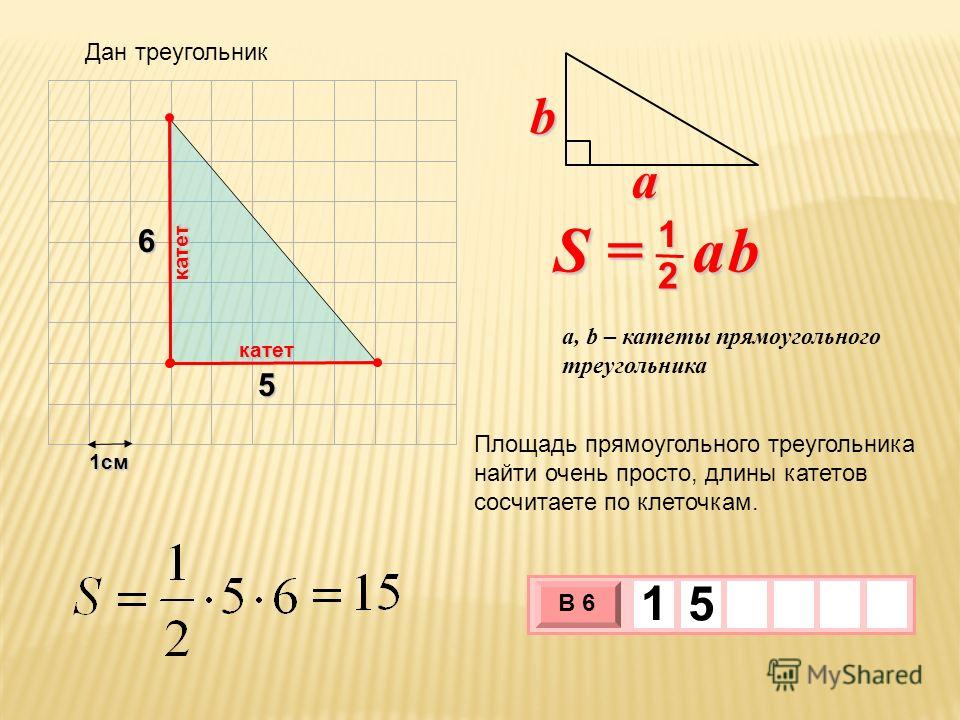 Для определения величины вам нужно рассчитать длину катетов. Это сделать просто по гипотенузе и косинусу прилежащего угла.

b=c×cos(α)

Узнав длину одного из катетов, по теореме Пифагора вы сможете рассчитать вторую сторону, выходящую из прямого угла.

b 2 =c 2 -a 2

В этой формуле c и a – гипотенуза и катет соответственно. Теперь можете рассчитать площадь по первой формуле. Точно так же можно вычислить один из катетов, имея второй и угол. В таком случае одна из искомых сторон будет равна произведению катета на тангенс угла. Существуют и другие способы вычисления площади, но зная основные теоремы и правила, вы сможете легко найти искомую величину.

Если у вас нет ни одной из сторон треугольника, а имеется лишь медиана и один из углов, то вы сможете вычислить длину сторон. Для этого используйте свойства медианы делить прямоугольный треугольник на два. Соответственно, она может выступать гипотенузой, если выходит из острого угла. Воспользуйтесь теоремой Пифагора и определите длину сторон треугольника, выходящих из прямого угла.

Как видите, зная основные формулы и Теорему Пифагора, вы сможете рассчитать площадь прямоугольного треугольника, имея лишь один из углов и длину одной из сторон.

Прямоугольный треугольник встречается в реальности практически на каждом углу. Знание о свойствах данной фигуры, а также умение вычислять ее площадь, несомненно пригодится вам не только для решения задач по геометрии, но и в жизненных ситуациях.

Геометрия треугольника

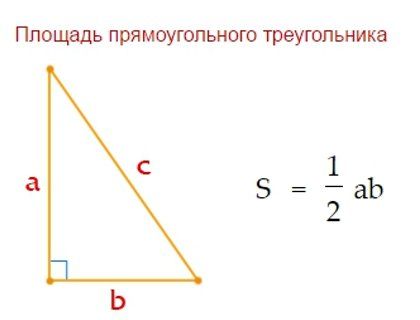
В элементарной геометрии прямоугольный треугольник — это фигура, которая состоит из трех соединенных отрезков, формирующих три угла (два острых и один прямой). Прямоугольный треугольник — оригинальная фигура, характеризующаяся рядом важных свойств, которые составляют фундамент тригонометрии. В отличие от обычного треугольника стороны прямоугольной фигуры имеют собственные названия:

• Гипотенуза — самая длинная сторона треугольника, лежащая напротив прямого угла.
• Катеты — отрезки, образующие прямой угол.
  В зависимости от рассматриваемого угла катет может быть прилежащим к нему (образующий этот угол с гипотенузой) или противолежащим (лежащим напротив угла). Для непрямоугольных треугольников катетов не существуют.

Именно соотношение катетов и гипотенузы составляет основу тригонометрии: синусы, тангенсы и секансы определяются как отношение сторон прямоугольного треугольника.

Прямоугольный треугольник в реальности

Данная фигура получила широкое распространение в реальности. Треугольники находят применение в проектировании и технике, поэтому расчет площади фигуры приходится выполнять инженерам, архитекторам и проектировщикам. Форму треугольника имеют основания тетраэдров или призм — трехмерных фигур, которые легко встретить в повседневности. Кроме того, угольник — наиболее простое представление «плоского» прямоугольного треугольника в реальности. Угольник — это слесарный, чертежный, строительный и столярный инструмент, который используется для построения углов как школьниками, так и инженерами.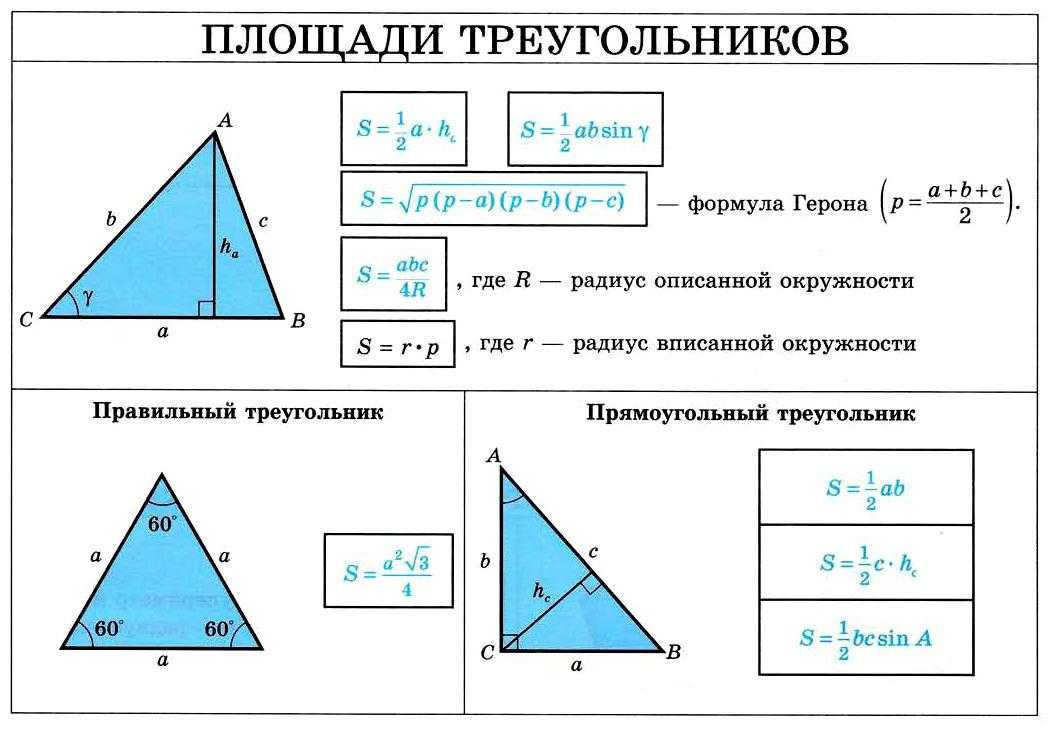

Площадь треугольника

Площадь геометрической фигуры — это количественная оценка того, какая часть плоскости ограничена сторонами треугольника. Площадь обычного треугольника можно найти пятью способами, используя формулу Герона или оперируя при расчетах такими переменными, как основание, сторона, угол и радиус вписанной или описанной окружности. Самая простая формула площади выражается как:

где a – сторона треугольника, h – его высота.

Формула для вычисления площади прямоугольного треугольника еще проще:

где a и b – катеты.

Работая с нашим онлайн-калькулятор, вы можете вычислить площадь треугольника, используя три пары параметров:

• два катета;
• катет и прилежащий угол;
• катет и противолежащий угол.

В задачах или бытовых ситуациях вам будут даны разные комбинации переменных, поэтому такая форма калькулятора позволяет вычислить площадь треугольника несколькими способами. Рассмотрим пару примеров.

Примеры из реальной жизни

Керамическая плитка

Допустим, вы хотите выполнить облицовку стен кухни керамической плиткой, которая имеет форму прямоугольного треугольника. Для того чтобы определить расход плитки вы должны узнать площадь одного элемента облицовки и общую площадь обрабатываемой поверхности. Пусть вам необходимо обработать 7 квадратных метров. Длина катетов одного элемента составляет по 19 см, тогда площадь плитки будет равна:

Это означает, что площадь одного элемента составляет 24,5 квадратных сантиметра или 0,01805 квадратных метра. Зная эти параметры, вы можете подсчитать, что для отделки 7 квадратных метров стены вам понадобится 7/0,01805 = 387 элементов облицовочной плитки.

Школьная задача

Пусть в школьной задаче по геометрии требуется найти площадь прямоугольного треугольника, зная только то, что сторона одного катета равна 5 см, а величина противолежащего угла составляет 30 градусов. Наш онлайн-калькулятор сопровождается иллюстрацией, на которой указаны стороны и углы прямоугольного треугольника. Если сторона a = 5 см, то ее противолежащий угол — это угол альфа, равный 30 градусов. Введите эти данные в форму калькулятора и получите результат:

Таким образом, калькулятор не только вычисляет площадь заданного треугольника, но и определяет длину прилежащего катета и гипотенузы, а также величину второго угла.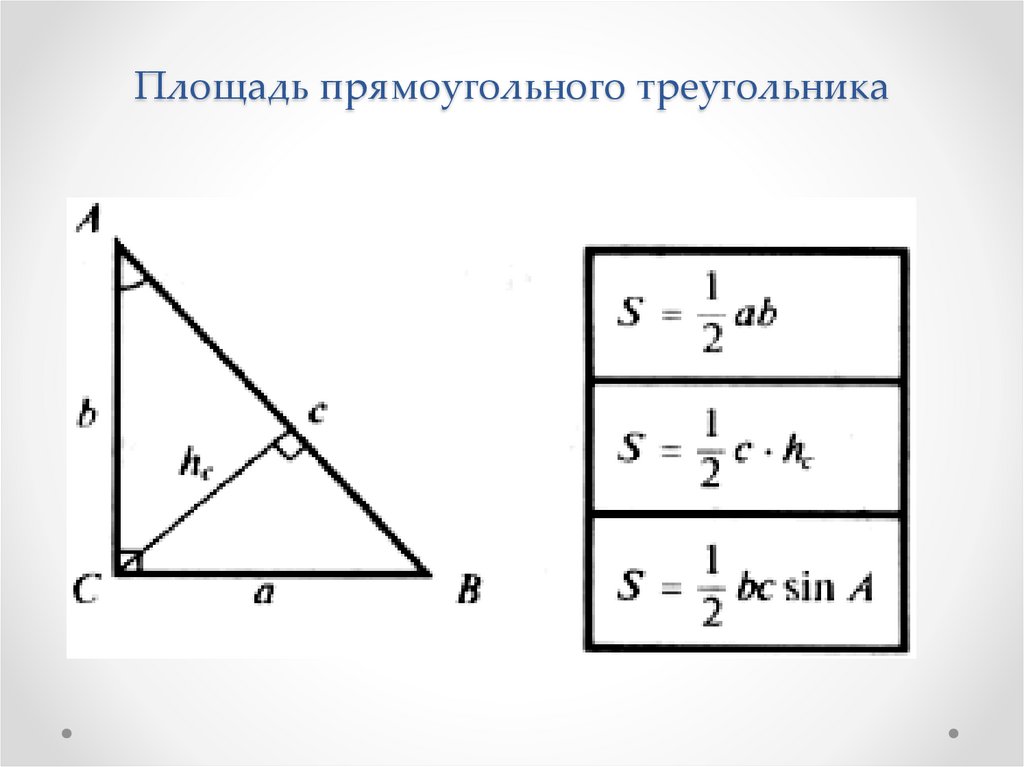

Заключение

Прямоугольные треугольники встречаются в нашей жизни буквально на каждом углу. Определение площади таких фигур пригодится вам не только при решении школьных заданий по геометрии, но и повседневной и профессиональной деятельности.

Площадь, примеры, типы и формула

Когда вы находитесь на краю прямоугольной или квадратной лужайки и намереваетесь добраться до соседнего конца, вы инстинктивно идете по диагонали к соседнему концу, потому что считаете, что это кратчайшее расстояние. Знаете ли вы, что вы образуете прямоугольный треугольник , когда идете по этому маршруту?

В этой статье мы узнаем больше о прямоугольных треугольниках и их свойствах.

Что такое прямоугольный треугольник?

А прямоугольный треугольник — это треугольник, в котором один угол прямой , то есть угол 90 градусов. Он также известен как прямоугольный треугольник .

Прямоугольные треугольники характеризуются квадратом, нарисованным на вершине их прямого угла, как показано ниже.

Изображение прямоугольного треугольника, StudySmarter Originals

Типы прямоугольных треугольников

Существует два типа прямоугольных треугольников.

Прямоугольный равнобедренный треугольник

равнобедренного прямоугольного треугольника имеет две стороны равной длины . То есть, кроме угла 90 градусов, его внутренние углы равны 45 градусам каждый.

Изображение равнобедренного прямоугольного треугольника — StudySmarter Originals

Равнобедренные прямоугольные треугольники используются для нахождения синуса, косинуса и тангенса угла в 45 градусов.

Разносторонний прямоугольный треугольник

Разносторонний прямоугольный треугольник не имеет равных сторон. Это означает, что один из его внутренних углов равен 90 градусов, а два других не равны, но в сумме дают 90 градусов.

Изображение разностороннего прямоугольного треугольника, StudySmarter Originals

Разнонаправленные прямоугольные треугольники используются для нахождения синуса, косинуса и тангенса двух специальных углов 30° и 60°.

Геометрия прямоугольных треугольников

Прямоугольный треугольник состоит из трех сторон, двух дополнительных углов и прямого угла. самая длинная сторона треугольника называется гипотенузой , и он противоположен прямому углу внутри треугольника. Две другие стороны обозначаются как основание и высота (или высота) .

Иллюстрация компонентов прямоугольного треугольника — StudySmarter Originals

Свойства прямоугольных треугольников углы должны быть равны 90 градусов.

2. Непрямые углы острые, то есть градусная мера каждого меньше 90 градусов.

Классифицируйте следующие углы, обозначенные от I до III.

1. Правые треугольники
2. Не правые треугольники
3. Правые треугольники
4. Правые треугольники

Решение:

Мы видим, что рис. до 90°. Однако обозначения на его сторонах показывают, что никакие две его стороны не равны. Это означает, что фигура I является разносторонним прямоугольным треугольником.

Однако на рисунке II ни один из его углов не равен 90º. Следовательно, фигура II — непрямоугольный треугольник.

Аналогично тому, что мы имеем на рисунке I, на рисунке III один из углов равен 90°. Это делает его прямоугольным треугольником. В отличие от фигуры I, фигура III имеет угол 45°, а это означает, что третий угол также будет равен 45°. Следовательно, это означает, что фигура III является равнобедренным прямоугольным треугольником, поскольку у него не только один из углов равен 90 °, но и два других угла равны. Следовательно, правильный ответ на этот вопрос:

а. Прямоугольные треугольники — I и III

б. Неправильный треугольник — II

c. Равнобедренный прямоугольный треугольник — III

d. Разносторонний прямоугольный треугольник — I

Периметр прямоугольных треугольников

периметр любой двумерной поверхности — это расстояние вокруг этой фигуры.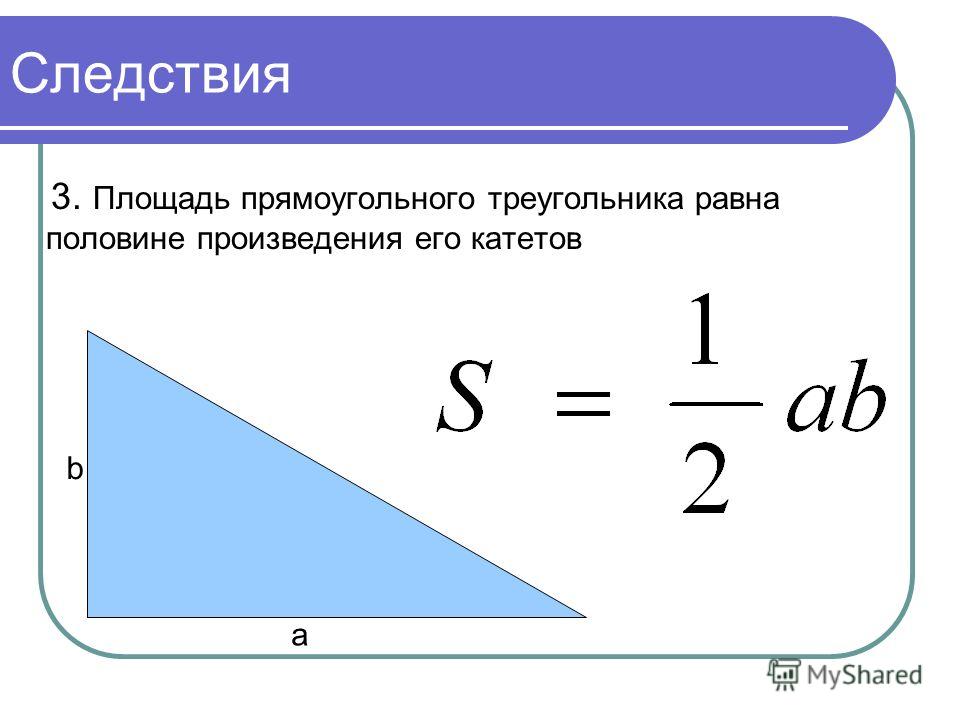 Таким образом, периметра прямоугольного треугольника — это сумма всех трех сторон: высоты, основания и гипотенузы.

Таким образом, периметр любого прямоугольного треугольника со сторонами a, b и c равен

Прямоугольный треугольник — StudySmarter Originals

Найдите периметр треугольника.

Решение:

Периметр треугольника равен сумме длин его сторон. Таким образом,

Площадь прямоугольного треугольника

Площадь прямоугольного треугольника можно вычислить путем умножения основания на высоту (или высоту) и деления результата на два.

В частности, чтобы найти площадь равнобедренного прямоугольного треугольника, нужно заменить либо основание на высоту, либо наоборот, так как высота и основание имеют одинаковую длину.

Цементный блок прямоугольного треугольника со сторонами 5 см, 13 см и 12 см используется для покрытия квадратного газона со стороной 30 см.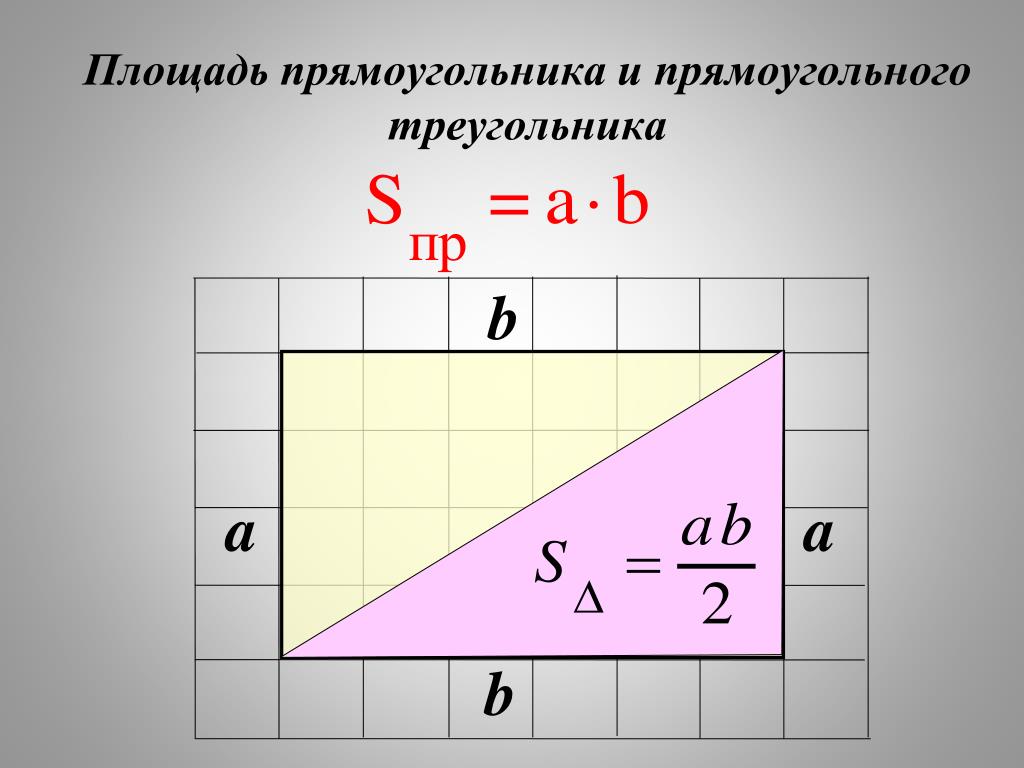 Сколько прямоугольных треугольников нужно, чтобы покрыть газон?

Решение:

Нам нужно определить площадь поверхности квадратного газона. Возьмем l за длину стороны квадратного газона, поэтому l = 30 м,

. чтобы заполнить квадрат.

Теперь площадь прямоугольного треугольника и квадрата вычислена, теперь мы можем определить, сколько прямоугольных цементных блоков можно найти на квадратном газоне.

Но сначала нам необходимо преобразовать M ² в CM ² , напомнив, что

Таким образом,

Поэтому один понадобится 300000 Правые трианги (5 см на 12 см. 13 см), чтобы покрыть квадратный газон длиной 30 м.

Примеры задач на прямоугольные треугольники

Еще несколько решаемых задач на прямоугольные треугольники, несомненно, проработаны лучше.

На рисунке ниже изображены два соединенных вместе прямоугольных треугольника. Найдите отношение площадей большего прямоугольного треугольника к площади меньшего, если гипотенуза большего прямоугольного треугольника равна 15 см.

Решение:

Так как длина гипотенузы большего прямоугольного треугольника равна 15 см, то гипотенуза меньшего прямоугольного треугольника равна

Нам нужно найти площадь большего прямоугольного треугольника, который равно A _b, и рассчитывается как:

Точно так же нам нужно найти площадь меньшего прямоугольного треугольника, который равен A _s, и рассчитывается как

Отношение площадей больший прямоугольный треугольник A _b меньшему прямоугольному треугольнику A _s равен

Прямоугольный треугольник имеет размеры 11 см на 15,6 см на 11 см. Какой это прямоугольный треугольник? Найдите периметр прямоугольного треугольника.

Решение:

Из вопроса, поскольку две стороны прямоугольного треугольника равны, это означает, что это равнобедренный прямоугольный треугольник .

Периметр прямоугольного треугольника равен

Прямоугольные треугольники — ключевые выводы

• Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть угол 90 градусов.
• Разносторонний и равнобедренный прямоугольные треугольники являются двумя типами прямоугольных треугольников.
• Прямоугольный треугольник состоит из трех сторон, дополнительной пары углов и прямого угла.
• Периметр прямоугольного треугольника суммы всех сторон.
• Площадь прямоугольного треугольника равна произведению половины его основания на высоту.

геометрия — Нахождение площади равнобедренного прямоугольного треугольника по его гипотенузе

спросил 4 года, 1 месяц назад

Изменено 9 месяцев назад

Просмотрено 7к раз

$\begingroup$

Я решал задачу, в которой мне сказали длины всех сторон равнобедренного треугольника и попросили найти площадь.

Я решил задачу, разделив равнобедренный треугольник на два равных треугольника, чтобы найти высоту, которую я использовал в формуле площади для исходного треугольника.

Глядя на ответ, мой метод дал правильное значение, но, похоже, я мог бы использовать стороны равнобедренного треугольника (обе по 8) в качестве основания и высоты и пропустить поиск высоты. Почему этот ярлык работает? Вопрос ниже:

7. Если гипотенуза равнобедренного прямоугольного треугольника равна $8 \sqrt 2$, какова площадь треугольника? 92$, поэтому треугольник прямоугольный, и вы можете сразу найти площадь как $\frac 12 (8)(8) = 32$.

   (В этом случае вам не нужно обратное. Это уже заданный треугольник. Но в случае, если вам даны длины сторон $(8,8,8\sqrt 2)$, вы можно применить обратное, чтобы немного упростить вашу работу).

   $\endgroup$

   $\begingroup$

   После редактирования OP, да, как указал Дипак в комментариях: это потому, что треугольник — это не просто равнобедренный треугольник, а равнобедренный правый треугольник.

   No related posts.