Формулы тангенсов синусов косинусов: синуса, косинуса, тангенса и котангенса

Основные формулы тригонометрии

Школа №67

Основные тригонометрические формулы

Выполнила

Шестак Анастасия

Руководитель: Синякова Е.А.

г.Владивосток

содержание

• Синус, косинус и тангенс углов
• Формулы сложения
• Синус, косинус и тангенс двойного угла
• Синус, косинус и тангенс половинного угла
• Формулы приведения
• Сумма и разность синусов.Сумма и разность косинусов.

• Радианная мера угла
• Поворот точки вокруг начала координат
• Определение синуса, косинуса и тангенса угла
• Знаки синуса, косинуса и тангенса
• Зависимость между синусом, косинусом и тангенсом одного и того же угла

Радианная мера угла

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

Найдем градусную меру угла в 1 радиан.

Так как дуга длиной R (полуокружность) стягивает центральный угол в , то дуга длиной R стягивает угол в раз меньший, т.е.

Так как = 3,14, то 1 рад = 57,3 .

Если угол содержит а радиан, то его градусная мера равна

0. Предположим, что точка, двигаясь по единичной окружности от точки Р(1;0) против часовой стрелки, прошла путь длиной (рис1).Конечную точку пути обозначим М. M y P(1;0) o x P(1;0) o x Рис 1 M Рис 2 В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол % рад. Поворот на 0 рад означает, что точка остается на месте. «

Поворот точки вокруг начала координат

Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности вокруг начала координат на угол рад, где -любое действительное число.

y

2.

Пусть

1.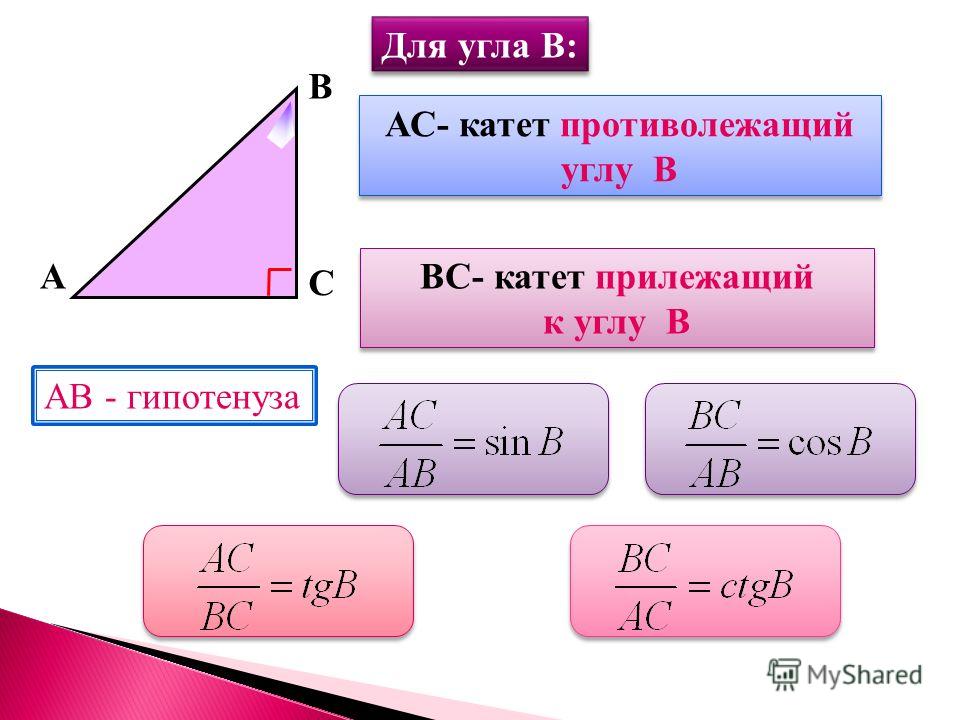 Пусть 0. Предположим, что точка, двигаясь по единичной окружности от точки Р(1;0) против часовой стрелки, прошла путь длиной (рис1).Конечную точку пути обозначим М.

M

y

P(1;0)

o

x

P(1;0)

o

x

Рис 1

M

Рис 2

В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол % рад.

Поворот на 0 рад означает, что точка остается на месте.

Определение синуса, косинуса и тангенса угла

Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол (обозначается sin )

Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол (обозначается cos )

В этих определениях угол может выражаться как в градусах, так и в радианах.

Тангенсом угла называется отношение синуса угла к его косинусу (обозначается tg )

Таким образом,

Иногда используется котангенс угла (обозначается ctg ), который определяется формулой

0 и cos 0, если (рис 3,4). Для точек, расположенных во второй четверти, ординаты положительны, а абсциссы отрицательны. Следовательно, sin 0, cos 0 (рис 3,4). 2. Знаки тангенса. По определению Поэтому tg 0, если sin и cos имеют одинаковые знаки, и tg y y y sin tg cos — + — + + + o o o o o o x x x + — — — — + Рис 5 Рис 3 Рис 4 «

Знаки синуса, косинуса и тангенса

1. Знаки синуса и косинуса . Пусть точка (1;0) движется по единичной окружности против часовой стрелки. Для точек, находящихся в первой четверти, ординаты и абсциссы положительны. Поэтому sin 0 и cos 0, если (рис 3,4).

Для точек, расположенных во второй четверти, ординаты положительны, а абсциссы отрицательны. Следовательно, sin 0, cos 0 (рис 3,4).

2. Знаки тангенса. По определению

Поэтому tg 0, если sin и cos имеют одинаковые знаки, и tg

y

y

y

sin

tg

cos

—

+

—

+

+

+

o

o

o

o

o

o

x

x

x

+

—

—

—

—

+

Рис 5

Рис 3

Рис 4

Зависимость между синусом, косинусом и тангенсом одного и того же угла

— основное тригонометрическое тождество.

Из него можно выразить sin через cos и cos через sin :

В этих формулах знак перед корнем определяется знаком выражения, стоящего в левой части формулы.

Выясним теперь зависимость между тангенсом и котангенсом. По

определению тангенса и котангенса

Перемножая эти равенства, получаем .

Из этого равенства можно выразить tg через ctg и наоборот:

Синус, косинус и тангенс углов и

Пусть точки М1 и М2 единичной окружности получены поворотом точки Р(1;0) на углы и соответственно (рис 6). Тогда ось 0х делит угол М10М2 пополам, и поэтому точки М1 и М2 симметричны относительно оси 0х.

Абсциссы этих точек совпадают, а ординаты отличаются только знаками. Точка М1 имеет координаты ( ), точка М2 имеет координаты .

Следовательно,

Используя определение тангенса, получаем .

Таким образом,

y

M 1

P(1;0)

o

х

М2

Рис 6

Формулы сложения

Теорема.

Для любых и справедливо равенство

Синус, косинус и тангенс двойного угла

Выведем формулы синуса и косинуса двойного угла, используя формулы сложения.

2.

Итак,

1.

Итак,

Полагая в формуле получаем

Синус, косинус и тангенс половинного угла

По известным значениям и можно найти значения и , если известно, в какой четверти лежит угол .

Из формулы при получаем (1)

Запишем основное тригонометрическое тождество в виде (2)

Складывая равенства (1) и (2) и вычитая из равенства (2) равенство (1), получаем (3)

(4)

Формулы (3) и (4) можно записать так: (5)

(6)

Разделив равенство (6) на равенство (5), получим формулу тангенса половинного угла

Формулы приведения

Таблицы значений синуса, косинуса, тангенса и котангенса составляются для углов от 0 до 90 (или от 0 до ). Это объясняется тем, что их значения для остальных углов сводятся к значениям для острых углов.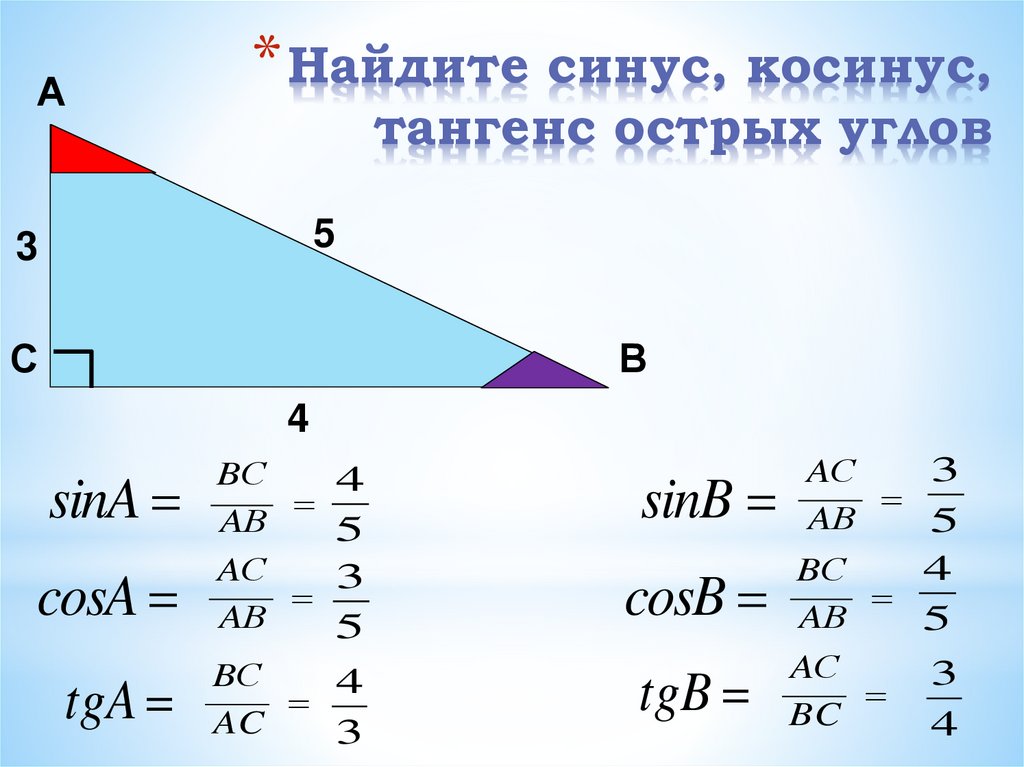

Вообще, формулами приведения для синуса называют следующие шесть формул:

Следующие шесть формул называют формулами приведения для косинуса:

Сумма и разность синусов. Сумма и разность косинусов.

Подведем итоги

Математика есть такая наука, которая показывает, как из знаемых количеств находить другие, нам еще неизвестные.

Д.С. Аничков

Математика действительно очень важна в жизни каждого человека. Ведь без нее никуда! А тригонометрические формулы являются ее неизменной частью. Надеюсь, моя презентация, посвященная именно тригонометрическим формулам поможем вам лучше разобраться в трудных моментах.

§ 2. Формулы сложения и их следствия

Так называются в тригонометрии формулы, позволяющие вычислить значение тригонометрической функции от суммы или разности двух чисел: sin (x + y), ctg (xy) и т.п. Вам потребуется вывести и запомнить формулы для вычисления синуса, косинуса и тангенса суммы и разности.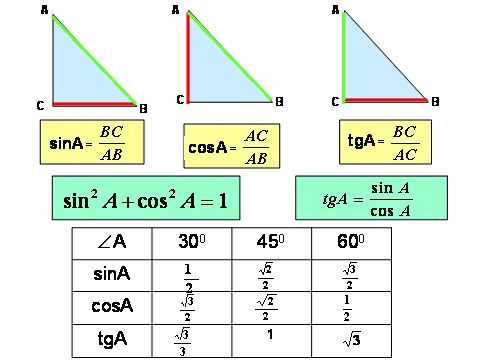 При этом будет удобно начать с доказательства формулы

cos(x y) = cosxcosy + sinxsiny,

которая выводится из двух формул скалярного произведения векторов.

Задача 4. Докажите формулу косинуса разности. Укажите ОДЗ для этой формулы.

Задача 5. Докажите формулу косинуса суммы. Укажите ОДЗ для этой формулы.

Задача 6. Докажите формулу cos (x) = sin x. Укажите ОДЗ для этой формулы.

Задача 7. Докажите формулу cos x = sin (x). Укажите ОДЗ для этой формулы.

Задача 8. Докажите формулы синуса суммы и разности. Укажите ОДЗ для каждой формулы.

Задача 9. Докажите формулы тангенса суммы и разности. Укажите ОДЗ для каждой формулы.

Из формул суммы получаются важные следствия  формулы приведения, позволяющие «привести» любое значение тригонометрической функции к значению ее для угла от 0⁰ до 45⁰ (или числа от 0 до ).

Задача 10. Опишите процедуру вывода всех формул приведения. Сопроводите рассказ необходимыми примерами. Опишите способ запоминания формул приведения. Сопроводите рассказ необходимыми примерами.

Из формул сложения естественно получаются формулы для кратных аргументов: 2х, 3х и т.д. Нужно уметь выводить и запомнить наизусть формулы синуса, косинуса и тангенса двойного угла.

Задача 11. Докажите формулы синуса, косинуса и тангенса двойного аргумента. Укажите ОДЗ для каждой формулы. Выведите также формулы синуса и косинуса тройного аргумента.

Формула косинуса двойного аргумента имеет еще два варианта, позволяющие найти формулы для половинного аргумента.

Задача 12. Выразите cos 2х через sin x и выведите формулу синуса половинного аргумента. Укажите ОДЗ для этой формулы.

Задача 13. Выразите cos 2х через cos x и выведите формулу косинуса половинного аргумента. Укажите ОДЗ для этой формулы.

Задача 14. Выведите три формулы тангенса половинного аргумента. Укажите ОДЗ для каждой формулы.

Из формул сложения получаются формулы, позволяющие преобразовать произведение синуса и косинуса двух аргументов в сумму и сделать обратное преобразование.

Задача 15. Выведите формулу произведения синусов. Укажите ОДЗ для каждой формулы.

Задача 16. Выведите формулу произведения косинусов. Укажите ОДЗ.

Задача 17. Выведите формулу произведения синуса и косинуса. Укажите ОДЗ.

Задача 18. Выведите формулу суммы синусов. Укажите ОДЗ.

Задача 19. Выведите формулу разности синусов. Укажите ОДЗ.

Задача 20. Выведите формулу суммы косинусов. Укажите ОДЗ.

Задача 21. Выведите формулу разности косинусов. Укажите ОДЗ.

Домашнее задание: Галицкий, Алгебра 8-9, глава 13, №№ 73-78, 80, 82, 84, 85, 87, 89, 91, 104, 105, 108, 109, 115-201.

Задача 22. Докажите что синус, косинус, тангенс и котангенс числа х являются функциями.

Задача 23.Установите область определения каждой из четырех тригонометрических функций: D(sin x), D(cos x), D(tg x) и D(ctg x).

Задача 24.Установите область значений каждой из четырех тригонометрических функций: Е(sin x), Е(cos x), Е(tg x) и Е(ctg x).

Прежде чем двигаться дальше, мы должны будем учесть два особых свойства тригонометрических функций, почти не встречавшихся нам до сих пор  их периодичность и их четность (нечетность).

Определение. Функция у = f(x) называется периодической, а число Т  0 называется ее периодом, если для каждого числа х, входящего в область определения этой функции, выполняются равенства f(x) = f(x + Т) = f(x Т).

Задание 27. Приведите примеры периодических функций из числа изученных вами вне курса тригонометрии.

Задание 28. Объясните, почему в определении периодической функции было бы недостаточно потребовать выполнения равенства f(x) = f(x + Т).

Задание 29. Докажите, что квадратичная функций не является периодической.

Задача 25. Докажите, что все четыре тригонометрические функции периодические и имеют периодом число 2.

Задача 26. Докажите, что функции y = sin x и y = соs x не имеют положительного периода, меньшего числа 2..

Задача 27. Докажите, что функции y = tg x и y = сtg x имеют наименьшим положительным периодом число .

Периодичность тригонометрических функций позволяет провести их исследование на каком-либо участке длиной в период, а затем распространить полученные результаты на другие участки области определения.

Еще более упрощается задача исследования тригонометрических функций ввиду их четности (нечетности).

Определение. Функция у = f(x) называется четной (или нечетной), если ее область определения симметрична относительно числа 0 и если для каждого числа х, входящего в область определения этой функции, выполняется равенство f(x) = f(x) (или f(x) = f(x)).

Задание 30. Приведите примеры четных и нечетных функций из числа изученных вами вне курса тригонометрии. Приведите пример функции, не являющейся ни четной, ни нечетной. Какая функция является и четной, и нечетной одновременно?

Задача 28. Докажите, что график четной функции симметричен относительно оси ординат.

Задача 29. Докажите, что график нечетной функции симметричен относительно начала координат.

Задача 30. Докажите, что косинус является четной функцией, а синус, тангенс и котангенс  нечетными функциями.

Четность (нечетность) тригонометрических функций позволяет провести их исследование лишь в первой четверти, а затем распространить результаты на всю область определения.

Функция синус

Начнем с функции y = sin x. Исследуем ее знак, монотонность и выпуклость на отрезке .

Задание 31. Установите знак синуса на отрезке .

Задание 32. Установите монотонность синуса на отрезке .

Чтобы доказать, что синус выпуклый вверх на отрезке , снова возьмем х₁ и х₂ из этого отрезка такие, что х₁ < х₂ , и докажем, что >

Задание 33. Постройте график синуса на отрезке , используя опорные точки (0; 0), , , и .

Задание 34. Постройте график синуса на отрезке.

Задание 35. Постройте график синуса на отрезке длиной в период синуса.

Задание 36. Постройте график синуса на всей области определения..

График функции синус называется синусоидой.

Имея строго обоснованный график синуса, мы можем окончательно сформулировать все свойства функции у = sin x:

Область определения: (∞;+∞).

Область значений: [1; 1].

Нули функции: n, nZ.

Функция положительна при x(2n; +2n), nZ; функция отрицательна при x(+2n; 2(n+1)), nZ.

Функция возрастает на , nZ; функция убывает на , nZ.

Функция периодическая с наименьшим положительным периодом 2.

Функция нечетная.

Функция выпукла вверх на [2n;  + 2n], nZ; функция выпукла вниз на

[ + 2n; 2n], nZ.

Функция косинус

Задача 31. Пользуясь тождеством сos x = sin (x+), постройте график косинуса преобразованием синусоиды. Выпишите все свойства косинуса, прочитав их на этом графике.

Функция тангенс

Задание 37. Установите знак, монотонность и выпуклость тангенса на полуинтервале .

Задание 38. Постройте график тангенса на полуинтервале, используя опорные точки.

Задание 39. Постройте график тангенса на всей его области определения.

График функции тангенс называется тангенсоидой.

Имея строго обоснованный график тангенса, мы можем окончательно сформулировать все свойства функции у = tg x:

Область определения:, nZ.

Область значений: (∞;+∞).

Нули функции: n, nZ.

Функция положительна при x, nZ; функция отрицательна при x, nZ.

Функция возрастает на каждом интервале своей области определения.

Функция периодическая с наименьшим периодом .

Функция нечетная.

Функция выпукла вверх на , nZ; функция выпукла вниз на , nZ.

Функция котангенс

Задача 32. Пользуясь тождеством сtg x =  tg (x+), постройте график котангенса преобразованием тангенсоиды. Выпишите все свойства котангенса, прочитав их на этом графике.

* * *

Среди известных вам выражений имеются попарно связанные, взаимно обратные: сумма и разность, произведение и частное, степень и корень. Тригонометрические выражения тоже имеют обратные: арксинус, арккосинус, арктангенс и арккотангенс. Первая часть наименований арк— переводится на русский язык с греческого словом «дуга».

Определения.

Арксинусом числа х (обозначение: arcsin x) называется такое число у  [ ], что sin у = х.

Арккосинусом числа х (обозначение: arcсоs x) называется такое число у  [0;], что соs у = х.

Арктангенсом числа х (обозначение: arctg x) называется такое число у  ( ), что tg у = х.

Арккотангенсом числа х (обозначение: arcctg x) называется такое число у  (0; ), что ctg у = х.

Задание 40. Докажите, что при введенных ограничениях введенные формулы задают функции.

Задача 33. Постройте график функции у = arcsin x и опишите ее свойства.

Задача 34. Постройте график функции у = arccos x и опишите ее свойства.

Задача 35. Постройте график функции у = arctg x и опишите ее свойства.

Задача 36. Постройте график функции у = arcctg x и опишите ее свойства.

Задание 41. С помощью координатной окружности найдите, если это возможно, a) arcsin (0,5), arcsin, arcsin ; б) arccos (0,5), arccos , arccos;

в) arctg, arctg 0; г) arcctg, arcctg 0.

Задание 42. Докажите следующие тождества:

а) arcsin x + arccos x = 0,5; б) arctg x + arcctg x = 0,5.

Задание 43. Решите уравнения, пользуясь координатной окружностью:

arcsin x = 0, arccos x = , arctg x =, arcctg x =,

arcsin x = 0,5, arccos x = , arctg x = , arcctg x = 0.

Домашнее задание: Виленкин, Алгебра 10, №№ 516,517,535,536,539,540,558,561,562.

Аналитическая тригонометрия Формулы сложения Cos и Tan

Дополнительные доказательства? Разве мы не можем вылечить корневой канал или вместо этого 10 часов слушать детский плач?

Мы могли бы сделать это, но это будет гораздо более болезненно, чем это будет. В прошлый раз мы сделали всю тяжелую работу; нахождение косинуса следует той же логике, что и синуса, просто мы используем разные строки в нашем ответе, что немного меняет окончательную формулу.

Снова начнем с:

Как и прежде, мы будем играть в числитель, разбивая его и перетасовывая кусочки.

На этот раз у нас есть вычитание, но идея та же. Теперь мы можем связать и с углом α, используя триггерные функции.

Теперь мы переставляем эти функции для линий и вставляем их обратно в уравнение формулы. У нас тут дежа вю.

Еще один набор замен на β и у нас есть формула сложения для косинуса.

cos (α + β) = cos (α) cos (β) – sin (α) sin (β)

Думайте о синусе и косинусе как о соперничающих командах по софтболу. Каждый угол придерживается своей команды — синус с синусом, косинус с косинусом — даже если у них есть друзья в другой команде. И у синуса очень плохой год; каким-то образом они набрали отрицательные очки на протяжении всего сезона. Никто даже не уверен, как они это сделали.

Пример задачи

Найдите точное значение cos (-135°).

Не паникуйте под таким отрицательным углом. У нас есть косинус, а косинус — четная функция ф (- х ) = ф ( х ).

Наш ответ будет таким же, как cos 135°. Видите, не нужно паниковать.

Есть несколько способов добраться до 135°. Используя наши специальные треугольники, мы можем использовать 135 ° = 30 ° + 45 ° + 60 °, что потребует двойного использования формулы сложения. Звучит не очень весело, но есть и другой вариант.

135° также равно 90° + 45°. Быстрый взгляд на графики y = sin x и y = cos x , или на единичной окружности, показывает, что sin (90°) равен 1, а cos (90°) равен 0. С этим достаточно легко работать, поэтому давайте использовать 90° + 45°

cos (90 + 45) = cos (90) cos (45) – sin (90) sin (45)

Эта формула может быть даже проще в использовании, чем формула синуса.

В родственной формуле

Нам еще нужно найти формулу сложения для тангенса. Однако отсюда становится легче, мы обещаем.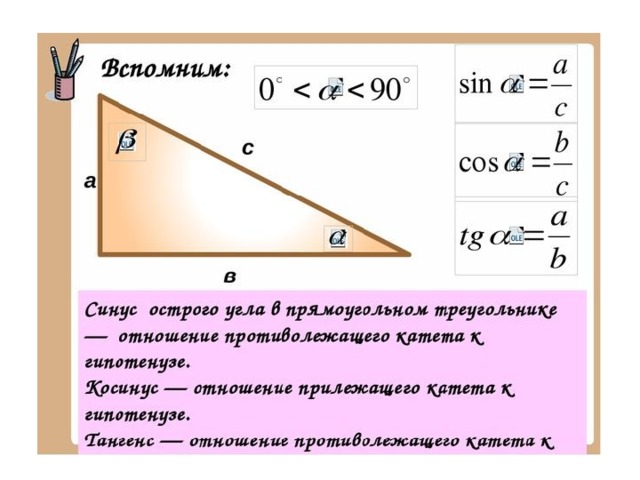 Обычно тангенс усложняет нам жизнь, но, может быть, он нас греет? Хитрость в том, что тангенс всегда равен синусу, а не косинусу.

Подобно бабочке, вырвавшейся из кокона, мы заменим в формулах сложения синус и косинус, чтобы получить красивое новое уравнение.

Ладно, это еще не красивая бабочка. Больше похоже на сонную осу. Но мы можем это исправить. Мы можем отменить некоторые термины и обменять некоторые из наших sin α, разделив все на cos α.

Выглядит немного лучше, но может понадобиться дополнительная помощь. Теперь разделим верх и низ на cos β:

Возможно, не все формулы могут быть бабочками. Но, по крайней мере, мы можем использовать этот, чтобы найти больше углов.

Пример задачи

Упрощение .

Математические войны: Радианцы наносят ответный удар. И на этот раз он принес с собой переменную. Однако мы все еще можем применить формулу.

Теперь мы просто принимаем специальный консультационный звонок с треугольником 30-60-90, чтобы максимально упростить. И в отличие от звонка на горячую линию экстрасенсов, это не стоит нам 4,9 доллара.9 в минуту.

Это может показаться более сложным, но на самом деле это просто. Мы мало что можем сделать с триггерной функцией, когда в ней застряло сложение.

Резюме

У нас есть три формулы для сложения углов.

• sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
• кос (α + β) = потому что (α) cos (β) – sin (α) sin (β)

Если ваш мозг полностью ограничен пространством, самое важное помнить о функциях сложения синуса и косинуса. Мы можем найти формулу сложения тангенсов (и некоторые другие, тсссс), используя их.

Но на самом деле у вас должна быть свободная комната или лишний хлам, который вы можете выбросить. Вам действительно нужно уметь цитировать Принцесса-невеста полностью от начала и до конца? (На самом деле да.)

Вывод формул двойного угла для синуса, косинуса и тангенса – Mean Green Math

John Quintanilla Помолвка, Приглашенный ведущий, Precalculus 17 июня 2022 г. 19 января 2022 г. 7 минут

На моем заключительном уроке для будущих учителей математики средней школы я прошу своих учеников придумать идеи для привлечения своих учеников к различным темам в учебной программе средней школы по математике. Другими словами, смысл задания заключался не в том, чтобы разработать полномасштабный план урока по этой теме. Вместо этого я попросил своих студентов подумать о трех различных способах заинтересовать их в этой теме. Я планирую поделиться некоторыми из лучших из этих идей в этом блоге (конечно, с разрешения моих студентов). Это студенческое представление исходит от моего бывшего студента Моргана Мэйфилда. Его тема из Precalculus: вывод формул двойного угла для синуса, косинуса и тангенса. Как вы, как учитель, могли бы создать задание или проект, связанный с вашей темой? Я хочу предоставить некоторое разнообразие возможностей, чтобы сделать это увлекательной возможностью для студентов, изучающих предварительный анализ, и некоторых студентов, изучающих математический анализ. Вот три моих мысли: ИДЕЯ 1: Для учащихся, изучающих предварительный анализ в обычном или углубленном классе, попросите их вывести эту формулу в группах. После того, как учащиеся познакомятся с тождествами Пифагора и тождествами суммы углов, сгруппируйте учащихся и попросите их вывести формулу для двойных углов Sin(2θ), Cos(2θ), Tan(2θ). Дайте им немного потрудиться и, если необходимо, дайте им несколько советов, таких как полезные формулы и способы представления умножения, чтобы оно выглядело как другие операции. Отсюда поощряйте учащихся к упрощению, когда они могут, и предложите учащимся найти другие формулы Cos (2θ). Попросите студентов предположить случаи, когда каждая формула для Cos(2θ) была бы полезной. Это дает ученикам уверенность в собственных силах и показывает, как взаимосвязана математика, а не просто набор тривиальных формул. Наконец, чтобы бросить вызов учащимся, попросите их придумать альтернативный способ доказательства Tan(2θ), особенно Sin(2θ)/Cos(2θ). Это было бы подходящим занятием для студентов, в то время как они продолжали бы практиковаться в доказательстве тригонометрических тождеств. ИДЕЯ 2: Эта следующая идея должна быть реализована для продвинутого класса Precal и только тогда, когда есть свободное время. Эйлер был умным человеком и оставил нам формулу Эйлера: . Попросите учащихся Precalculus приостановить свои вопросы о том, откуда они взялись и для чего они используются. Это не то, что они будут использовать в своем классе. Убедите их, что для того, что они будут делать, все, что им нужно, это понимать мнимые числа, умножение мнимых чисел и законы степени. Пусть они подставят x = A + B и упростят правую часть уравнения, чтобы мы получили: где и — два действительных числа. Здесь цель получить. Все шаги, чтобы добраться до этой точки, — это алгебра, они ничего не могут понять. Теперь следующая часть — заставить их мозги задуматься о том, какой смысл мы можем придать этому. Если они борются, попросите их подумать о последствиях равенства двух воображаемых чисел; коэффициенты действительной части и мнимой части должны быть равны друг другу. Наконец, спросите их, кажутся ли эти уравнения знакомыми, откуда они и как они называются… формулами суммы углов. Отсюда это может привести к тому, что, если x = 2A? Студенты либо переберут формулу снова, а другие поймут, что x = A + A, и подставят ее к уравнению, которое они только что вывели, и упростят. Эта идея представляет собой кражу 2-в-1 для формул суммы углов и формул двойного угла. Это самый большой недостаток, это для Sin(2 θ ) и Cos(2 θ ).   ИДЕЯ 3: Возьмите ИДЕЮ 2 и поместите ее в класс исчисления 2. Все, что остается в классе предварительного исчисления, но теперь учащиеся в парах доказывают формулу Эйлера, используя ряды Тейлора. Проведите их через использование ряда Тейлора, чтобы выяснить представление ряда Тейлора для , ,  и . Затем попросите учащихся найти расширенный ряд Тейлора, состоящий из 12 терминов с многоточием, не нужно оценивать каждый термин, только точный термин. Дайте подсказки, такие как и рассмотреть и другие подобные случаи. Наконец, попросите учащихся разделить расширенный ряд таким образом, чтобы имитировать использование эллипсов, чтобы показать, что ряды уходят в бесконечность. То, что они должны найти, выглядит примерно так:

Выглядит знакомо? Ну, это добавление двух рядов Тейлора, которые представляют Sin (x) и Cos (x). Это последняя связь, которую ученики должны установить. Дайте подсказки, чтобы просмотреть их заметки, чтобы понять, почему «а» и «б» в воображаемом числе выглядят такими знакомыми. Это всего лишь один из способов доказать формулу Эйлера, затем вы можете продолжить с ИДЕЕЙ 2, пока ваши ученики не докажут формулы суммы углов и формулы двойного угла.

Как эта тема расширяет то, что ваши студенты должны были изучить на предыдущих курсах? Студенты в Техасе, как правило, знакомятся с теоремой Пифагора в 8–9 годах.0152-й класс. На этом этапе учащиеся используют для нахождения длины недостающей стороны. На этом этапе учащиеся также могут познакомиться с пифагорейскими тройками. Затем на уровне геометрии или в разделе тригонометрии учащиеся познакомятся с пифагорейской идентичностью. Личность есть. Я думаю, что это несправедливо по отношению к студентам просто изучать это тождество, не связывая его с теоремой Пифагора. Я думаю, что было бы хорошей задачей для студента решить это тождество, используя прямоугольный треугольник с гипотенузой c, чтобы Sin (θ) = b/c и cos (θ) = a/c, тогда можно было бы показать либо и, следовательно, либо можно показать (используя теорему Пифагора). Отсюда учащиеся узнают о формулах сложения и вычитания углов в Precalculus. Это все, что им нужно для вывода формул двойного угла.

Это было бы хорошим упражнением, которое учащиеся могут выполнить в парах. Sin(2θ) = Sin(θ + θ), Cos(2θ) = Cos(θ + θ), Tan(2θ) = Tan(θ + θ). Теперь мы можем применить формулу суммы углов, где оба угла равны: Sin(2θ) = sin(θ)cos(θ) + cos(θ)sin(θ) = 2sin(θ)cos(θ) Cos(2θ) = cos(θ)cos(θ) – sin(θ)sin(θ) =  (здесь мы используем тождество Пифагора) Тан(2θ) = Бонусная задача: используйте Sin(2θ) и Cos(2θ), чтобы получить Tan(2θ). Ну а если , то

Выводы просты, и я полагаю, что многие студенты сорвутся с крючка, не имея возможности вывести множество тригонометрических тождеств и приняв их за факты. Это в пределах досягаемости в среднем от 10 ^th до 12 ^th грейдеров.

Каков вклад различных культур в эту тему? Я включил четыре ссылки, которые рассказывают об истории тригонометрии. Казалось, что древним обществам нужно было знать о пифагорейских тождествах и формулах суммы углов, чтобы знать формулы двойного угла. Вот наша проблема, трудно понять, кто «сделал это первым?» и когда «знали ли они это?». Математические доказательства и история хранились не как аккуратно записанные записи, а как устные традиции, развлечения, хобби и профессии. Правда в том, что, насколько я читал, многие культуры понимали формулу двойного угла в некоторой степени независимо друг от друга, даже если не было никаких формальных доказательств или записей об этом. Оглядываясь назад на мой ответ на B2, кажется, что формула двойного угла почти как следствие знания формул суммы углов, и, таким образом, понимание одного может подразумевать знание другого. Возможно, просто не считалось важным выделять формулу двойного угла в отдельную категорию. Многие из тех, кто разобрался в этих тождествах, делали это потому, что были астрономами, навигаторами или плотниками (строитель). Треугольники и круги очень важны для этих профессий. Знание формулы суммы углов было известно в Древнем Китае, Древней Индии, Египте, Греции (первоначально в виде теоремы Архимеда о сломанных хордах) и более широком «средневековом исламском мире». Обратите внимание, что Египет, Греция и средневековый исламский мир были сильно переплетены, поскольку находились на восточной стороне Средиземного моря и являлись важными центрами знаний (например, Александрийской библиотекой). Вот в чем дело, их знания не всегда демонстрировались в так же, как мы знаем это сегодня. В некоторых культурах действительно были функции, подобные современным тригонометрическим функциям сегодня, и индийский математик Мадхава из Сангамаграмы вычислил аппроксимацию этих функций рядом Тейлора в 1400-х годах.