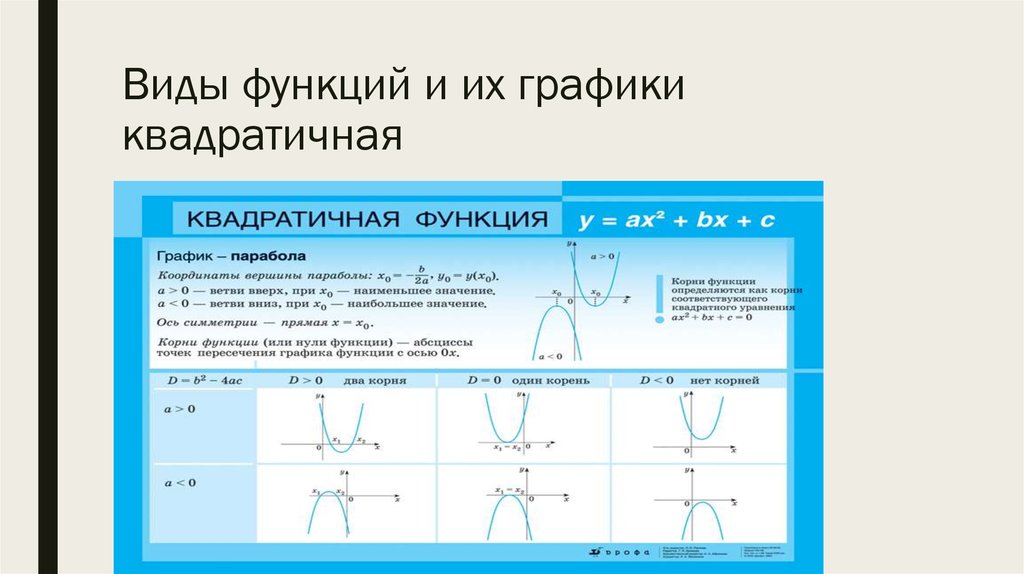
Элементарные функции и их графики
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
1. Степенные
К этому типу относятся линейные, квадратичные, кубические, , , . Все они содержат выражения вида xα.
2. Показательные
Это функции вида y = ax.
3. Логарифмические
y = logax.
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
5. Обратные тригонометрические
Содержат arcsinx, arccosx, arctgx, arcctgx.
Элементарными они называются, потому что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x2 · ex — произведение квадратичной и показательной функций; y = sin(ax) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.
Степенные функции
| 1. Линейная функция y = x | |
| 2. Квадратичная парабола y = x2 | |
| 3. Функция y = xn, n — натуральное, n > 1 n — чётное n = 2, 4, 6,… | |
| n — нечётное n = 3, 5, 7,… | |
| 4.Гипербола | |
| 5. | |
| 6. |
Показательная функция y = ax
| a > 1 | |
| 0 < a < 1 |
Логарифмическая функция y = logax
| a > 1 | |
| 0 < a < 1 |
Тригонометрические функции
1. | |
| 2. | |
| 3. | |
| 4. |
Обратные тригонометрические функции
| 1. | |
| 2. | |
| 3. | |
| 4. |
Выше приведены основные, «базовые» графики. А как будут выглядеть, например, графики функций y = sin(2x) или y = 4x
Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций.
Почему в уравнении 3x = 35 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3x возрастает и каждое значение принимает только один раз.
Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.
Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически.
Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки».
Алгебра Свойства функции
Материалы к уроку
Конспект урока
Чтобы узнать, какими свойствами обладает функция, рассмотрим несколько примеров.
На рисунке изображен график зависимости температуры воздуха от времени суток. На оси икс указано время суток в часах, на оси игрек – температура воздуха в градусах Цельсия. Мы видим, что в течение первых пяти часов температура понижалась, с пяти до шестнадцати часов – повышалась, а затем снова понижалась. Таким образом, с помощью графика мы определили некоторые свойства функции, определяющей зависимость температуры воздуха от времени суток.
Таким образом, с помощью графика мы определили некоторые свойства функции, определяющей зависимость температуры воздуха от времени суток.
Рассмотрим теперь свойства функции игрек равно эф от икс, где икс больше либо равно минус шести и меньше либо равно пяти. Выясним, при каких значениях икс функция обращается в ноль, принимает положительные и отрицательные значения.
На рисунке видно, что функция принимает значение, равное нулю при икс равном минус трем и икс равном четырем. Значения аргумента, при которых функция обращается в ноль, называют нулями функции, то есть числа минус три и четыре – нули рассматриваемой функции. Нули функции разбивают ее область определения – промежуток от минус шести до пяти на три промежутка: от минус шести до минус трех (включая шесть), от минус трех до четырех и от четырех до пяти (включая пять). Для значений икс из промежутка от минус трех до четырех точки графика расположены выше оси икс, а для остальных промежутков – ниже оси икс. Значит, в промежутке от минус трех до четырех функция принимает положительные значения, а в двух других – отрицательные.
Промежутки, в которых функция сохраняет знак, называют промежутками знакопостоянства…
Выясним теперь, как изменяются значения данной функции с изменением икс.
Из графика видно, что с возрастанием икс от минус шести до единицы значения игреков увеличиваются, а с возрастанием икс от единицы до пяти значения игрек уменьшаются. Говорят, что в промежутке от минус шести до единицы, включая числа минус шесть и один, функция является возрастающей, а в промежутке от единицы до пяти, включая числа один и пять, эта функция является убывающей.
Таким образом, можно сказать, что функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией.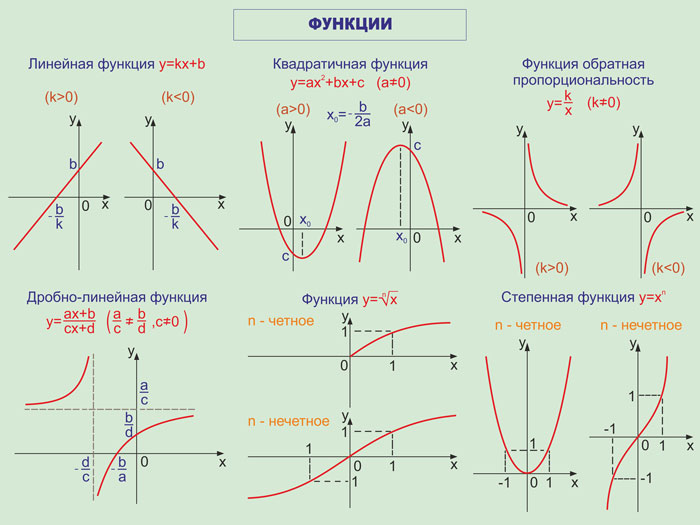
На рисунках изображены графики возрастающей и убывающей функций соответственно…..
Сейчас мы выясним, какими свойствами обладают ранее изученные нами функции.
Рассмотрим свойства линейной функции игрек равно ка икс плюс бэ, где ка не равно нулю.
- Функция обращается в ноль при икс равном отношению минус бэ и ка. Для доказательства решим уравнение ка икс плюс бэ равно нулю. Получим, что игрек равен нулю при икс равном отношению минус бэ и ка.
- При ка большем нуля функция принимает отрицательные значения в промежутке от минус бесконечности до минус бэ делённого на ка и положительные значения в промежутке от минус бэ деленного на ка до плюс бесконечности. Убедиться в этом можно решив неравенства ка икс плюс бэ меньше нуля и ка икс плюс бэ больше нуля. Если ка больше нуля, то игрек меньше нуля при икс меньшем минус бэ деленного на ка.. и игрек больше нуля при икс большем минус бэ деленного на ка. При ка меньшем нуля функция принимает отрицательные значения в промежутке от минус бэ деленного на ка до плюс бесконечности и положительные значения в промежутке от минус бесконечности до бэ деленного на ка.
 Это следует из решения неравенства ка икс плюс бэ меньше нуля и ка икс плюс бэ больше нуля при условии, что ка меньше нуля.
Это следует из решения неравенства ка икс плюс бэ меньше нуля и ка икс плюс бэ больше нуля при условии, что ка меньше нуля. - При ка большем нуля функция игрек равно ка икс плюс бэ является возрастающей, а при ка меньшем нуля – убывающей. Докажем это. Пусть икс первое и икс второе – произвольные значения аргумента, причем икс первое больше икс второго. Игрек первое и игрек второе – соответствующие им значения функции: игрек первое равно ка икс первое плюс бэ, и игрек второе равно ка икс второе плюс бэ. Рассмотрим разность игрек второе и игрек первое. Она будет равна произведению ка и разности между икс второе и икс первое. Второй множитель положителен, так как икс второе больше икс первое. Поэтому знак произведения ка и разности между икс второе и икс первое определяется знаком коэффициента ка. Если ка больше нуля, то произведение ка и разности между икс второе и икс первое больше нуля и игрек первое больше игрек второго. Значит, при ка большем нуля функция игрек равно ка икс плюс бэ является возрастающей.

Рассмотрим свойства функции игрек равно ка деленное на икс, где ка не равно нулю.
- Функция нулей не имеет. Это следует из того, что ка деленное на икс при любом значении аргумента не обращается в ноль, так как по условию ка не равно нулю.
- Функция игрек равно ка деленное на икс при ка большем нуля принимает отрицательные значения в промежутке от минус бесконечности до нуля и положительные значения в промежутке от нуля до плюс бесконечности. Действительно, если ка больше нуля, то ка деленное на икс меньше нуля при икс меньшем нуля, и ка деленное на икс больше нуля при икс большем нуля. Функция игрек равно ка деленное на икс при ка меньшем нуля принимает отрицательные значения в промежутке от нуля до плюс бесконечности и положительные значения в промежутке от минус бесконечности до нуля.
 Обоснование этого аналогично изложенному для случая, когда ка больше нуля.
Обоснование этого аналогично изложенному для случая, когда ка больше нуля. - При ка большем нуля функция игрек равно ка деленное на икс является убывающей в каждом из промежутков от минус бесконечности до нуля и от нуля до плюс бесконечности, а при ка меньшем нуля – возрастающей в каждом из этих промежутков. Доказательство этого свойства проводится аналогично тому, как это было сделано для линейной функции.
Заметим, что хотя функция игрек равно ка деленное на икс, где ка не равно нулю, убывает или возрастает в каждом из промежутков от минус бесконечности до нуля и от нуля до плюс бесконечности, она не является убывающей или возрастающей функцией на всей области определения.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Функции и отношения изучайте онлайн
Улучшайте свои оценки, развлекаясь
и получите мгновенный доступ ко всему контенту!
Попробуйте 30 дней БесплатноСодержание
Введение
Упорядоченная пара представляет собой набор входов и выходов и представляет отношение между двумя значениями. Отношение представляет собой набор входов и выходов, а функция представляет собой отношение с одним выходом для каждого входа.
Отношение представляет собой набор входов и выходов, а функция представляет собой отношение с одним выходом для каждого входа.
Что такое функция?
Некоторые отношения имеют смысл, а другие нет. Функции — это отношения, которые имеют смысл. Все функции являются отношениями , но не все отношения являются функциями.
Функция – это отношение, согласно которому для каждого входа имеется только один выход.
Вот отображения функций. Домен — это вход или x-значение , а диапазон — это выход или y-значение .
Каждое значение x связано только с одним значением y.
Хотя входы, равные -1 и 1, имеют одинаковый выход, это отношение по-прежнему является функцией, поскольку каждый вход имеет только один выход.
Это сопоставление не является функцией. Вход для -2 имеет более одного выхода.
Графические функции
Использование входных и выходных данных, перечисленных в таблицах, картах и списках, позволяет легко наносить точек на координатную сетку . Используя график точек данных, вы можете определить, является ли отношение функцией, используя проверка вертикальной линии . Если вы можете провести вертикальную линию через график и коснуться только одной точки, отношение является функцией.
Используя график точек данных, вы можете определить, является ли отношение функцией, используя проверка вертикальной линии . Если вы можете провести вертикальную линию через график и коснуться только одной точки, отношение является функцией.
Взгляните на график этой карты отношений. Если бы вы провели вертикальную линию через каждую из точек на графике, каждая линия соприкасалась бы только в одной точке, поэтому это отношение является функцией.
Специальные функции
Специальные функции и их уравнения имеют узнаваемые характеристики.
Постоянная функция
$f(x) = c$
Значение c может быть любым числом, поэтому график постоянной функции представляет собой горизонтальную линию. Вот график $f(x) = 4$
Функция тождества
$f(x) = x$
Для функции тождества значение x совпадает со значением y . График представляет собой диагональную линию, проходящую через начало координат.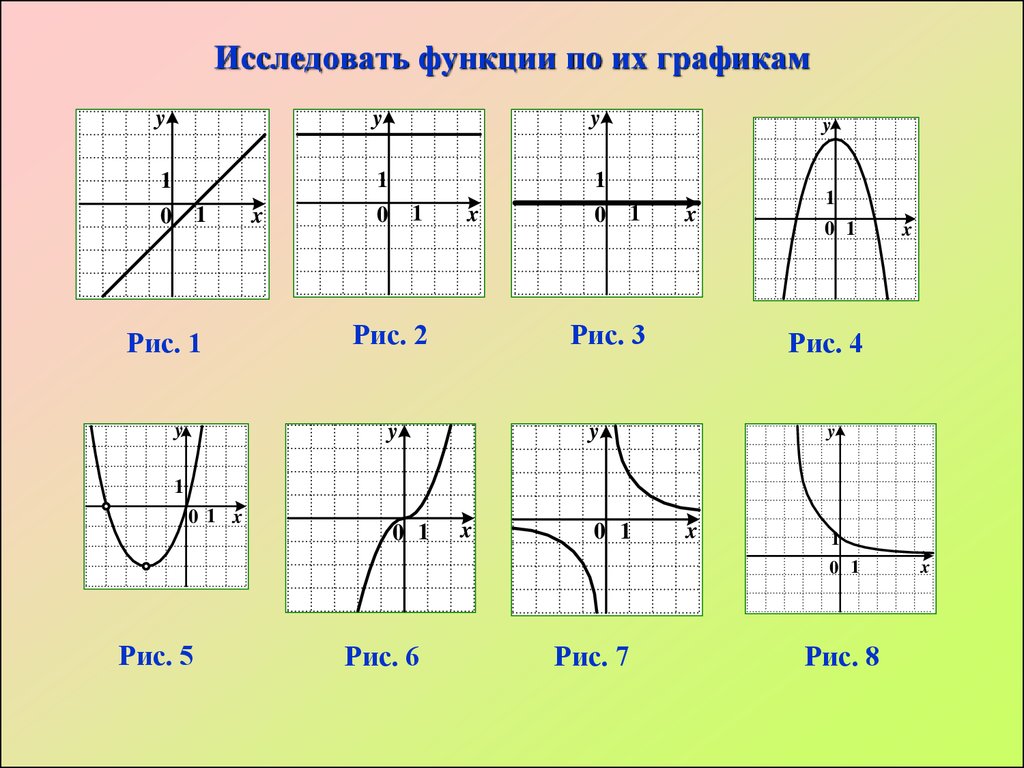
Линейная функция
$f(x) = mx + b$
Уравнение, записанное на Форма пересечения наклона представляет собой уравнение линейной функции , а график функции представляет собой прямую линию.
Вот график $f(x)= 3x +4$
Функция абсолютного значения
$f(x) = |x|$
Функцию абсолютного значения легко узнать по ее V-образный график. График состоит из двух частей и является одной из кусочных функций.
Это лишь некоторые из наиболее распространенных специальных функций. 9{-1}(x) =\frac{x + 4}{3}$.
Не всякая обратная функция является функцией, поэтому для проверки используйте тест вертикальной линии.
Операции с функциями
Вы можете складывать, вычитать, умножать и делить функции .
- $f(x) + g(x) = (f + g)(x)$
- $f(x) — g(x) = (f — g)(x)$
- $f(x) \times g(x) = (f \times g)(x)$
- $\frac{f(x)}{g(x)}= \frac{f}{g}(x)$
Посмотрите на два примера операций функции:
{2} + 11х + 28 \end{выравнивание}$Все
видео по теме Видео по темеФункции и отношения (7 видео)
Что такое функция? Разница между функциями и отношениями
03:51 мин
Упражнение
Рабочие листы
Функциональные операции
07:45 мин
Упражнение
Рабочие листы
Обратные функции
05:03 мин
Упражнение
Рабочие листы
Графические функции
04:58 мин
Упражнение
Рабочие листы
Преобразование между таблицами, графиками, отображениями и списками точек
04:03 мин
Упражнение
Рабочие листы
Линейные и нелинейные функции
03:50 мин
Упражнение
Рабочие листы
Специальные функции
05:51 мин
Упражнение
Рабочие листы
Все
рабочих листов по теме Рабочие листы по темеФункции и отношения (7 рабочих листов)
- Что такое функция? Разница между функциями и отношениями
Показать PDF
- Функциональные операции
Показать PDF
- Обратные функции
Показать PDF
- Графические функции
Показать PDF
- Преобразование между таблицами, графиками, отображениями и списками точек
Показать PDF
- Линейные и нелинейные функции
Показать PDF
- Специальные функции
Показать PDF
Обучающие функции в алгебре 1
Автор Тайн Брэк29 августа
389 акции
- Поделиться
Функции не только забавны, но и являются основой всей Алгебры 1 — линейной, квадратичной и экспоненциальной. Из 49 техасских стандартов в алгебре 1 20 включают функции — это более 40%! Важно, чтобы учащиеся четко понимали, как идентифицировать, оценивать и графически отображать функцию, чтобы подготовить их к решению более сложных задач.
Из 49 техасских стандартов в алгебре 1 20 включают функции — это более 40%! Важно, чтобы учащиеся четко понимали, как идентифицировать, оценивать и графически отображать функцию, чтобы подготовить их к решению более сложных задач.
Стандарты
Вот стандарты, которые лучше всего описывают то, на чем мы сегодня сосредоточим свое внимание.
- A.12(B) оценивают функции, выраженные в виде функций, по одному или нескольким элементам в их областях определения
- A.12(A) решить, определяют ли отношения, представленные словесно, таблично, графически и символически, функцию
Вот как выглядят эти стандарты в виде тестовых вопросов STAAR 2019 и 2018 годов.
Выравнивание по вертикали
В 8-м классе учащиеся начнут определять функции в упорядоченных парах и с помощью графиков; это стандарт готовности, поэтому он более тщательно проверяется в 8-м классе, чем в алгебре 1. Вы можете увидеть пример тестового вопроса STAAR для 8-го класса ниже.
Я думаю, что вертикальное выравнивание — это одна из вещей, которую учителя чаще всего упускают из виду при планировании урока. Если вы не уверены, посмотрите, с чем учащиеся уже познакомились, прежде чем вводить тему. Мне нравится использовать этот документ здесь.
Идентификация функций
Если вы раньше учили, как идентифицировать функцию, вы, вероятно, знакомы с определением функции —
«Функция — это правило, которое назначает каждому входу ровно один выход. Они возникают, когда каждое значение x связано ровно с одним значением y».
Вероятно, вы хорошо знакомы с тестом вертикальной линии.
Когда я был студентом, я научился просто использовать тест вертикальной линии. Если бы у меня был набор упорядоченных пар, я бы быстро зарисовал его, чтобы увидеть, прошел ли он тест вертикальной линии. У меня НЕ было понимания, почему это сработало и что сделало функцию реальной функцией.
Только когда я преподавал функции, я столкнулся с концепцией, которая помогла мне понять, ПОЧЕМУ стоит тест вертикальной линии.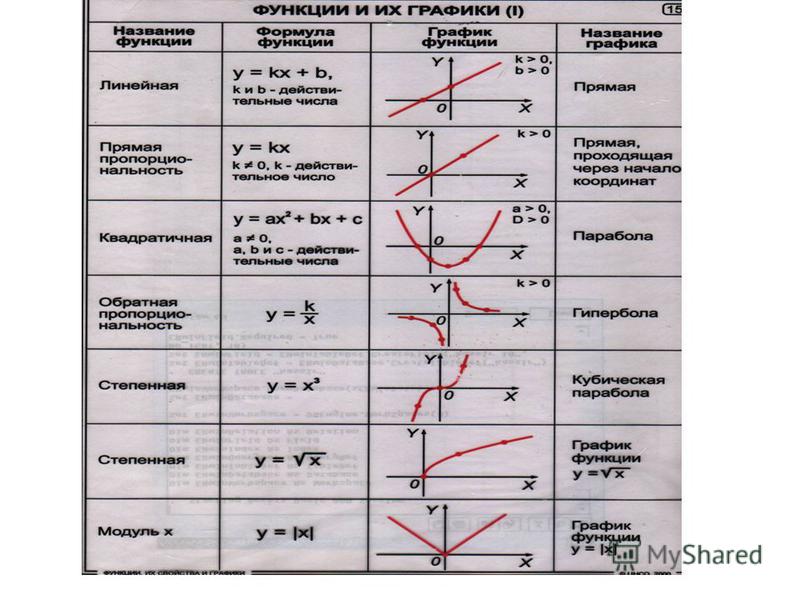 Если у вас есть график со временем по оси x и расстоянием по оси y, вертикальная линия будет представлять кого-то или что-то в определенный момент времени, находясь более чем в одном месте одновременно, что невозможно. Горизонтальная линия будет представлять кого-то или что-то неподвижное в течение возможного периода времени.
Если у вас есть график со временем по оси x и расстоянием по оси y, вертикальная линия будет представлять кого-то или что-то в определенный момент времени, находясь более чем в одном месте одновременно, что невозможно. Горизонтальная линия будет представлять кого-то или что-то неподвижное в течение возможного периода времени.
Вот другие стратегии, которые помогут учащимся концептуально понять:
- Пример торгового автомата: Кнопки — это ввод. Выпивка – это выход. A1 даст вам колу. А2 может дать тебе кокаин. Но А3 не может дать вам спрайт или кока-колу.
- Пример быстрого набора на телефоне: X — это номер, который вы набираете, а y — человек, которому звонят. Ваш телефон работает, когда вы нажимаете 3, и он звонит только вашей маме, или если вы нажимаете 4, и он звонит вашему брату. Телефон НЕ работает, если вы нажмете 3, и он иногда идет к вашей маме, а иногда к вашему брату. Однако вы можете запрограммировать два номера на одного и того же человека.
- Несколько учеников могут быть одного роста, но один ученик не может быть разного роста.

Вычисление функций и построение графиков
Как только учащиеся получат четкое представление о функциях и отношениях, вычисление функций и построение графиков станут немного более естественными. С 6-го класса учащиеся заменяют и рисуют графики во всех четырех квадрантах. Потратьте время на изучение порядка операций и способов построения графика на координатной плоскости. Никогда не думайте, что учащиеся уже знают, как это сделать — вы будете удивлены неправильными представлениями! Однако обозначение функций будет новым для учащихся. По моему опыту, студенты достаточно хорошо понимают, что f(x) — это новый y!
Используйте технологии для реальных приложений
И поскольку ничто так не оживляет математику, как наша любимая веб-программа, вот несколько ссылок на Desmos.
- Угадай мое правило: учащиеся знакомятся с концепцией функции, используя пары ввода-вывода в таблице. Они исследуют различные правила, некоторые из которых являются функциями, а некоторые — нет.

- Сортировка карточек — функции: в этом упражнении учащиеся сортируют графики, уравнения и контексты в зависимости от того, представляет ли каждый из них функцию.
Шаг
Свойства функций – идентификация, оценка и построение графиков – это большие навыки, которые требуют отдельного дня. Каждый из этих навыков требует понимания учащимися множества форматов — набора упорядоченных пар, картографических диаграмм, графика, таблицы или примера из реальной жизни. Ученикам нужно знакомство, поэтому не планируйте проходить эти стандарты за несколько дней. Поскольку функции являются основополагающими в алгебре, дополнительное время, потраченное на подготовку сцены, не будет потрачено впустую.
Готовы научить!? Вы можете найти наш блок свойств функций здесь (+ домен и диапазон)!
Если вам нужны практические свойства действий функций, вы можете найти их здесь (+ домен и диапазон)!
Что мне также нравится в этом особом навыке, так это то, что он мягко представляет все типы функций, с которыми учащиеся будут работать в течение года, — линейные, квадратичные и экспоненциальные.

 Это следует из решения неравенства ка икс плюс бэ меньше нуля и ка икс плюс бэ больше нуля при условии, что ка меньше нуля.
Это следует из решения неравенства ка икс плюс бэ меньше нуля и ка икс плюс бэ больше нуля при условии, что ка меньше нуля.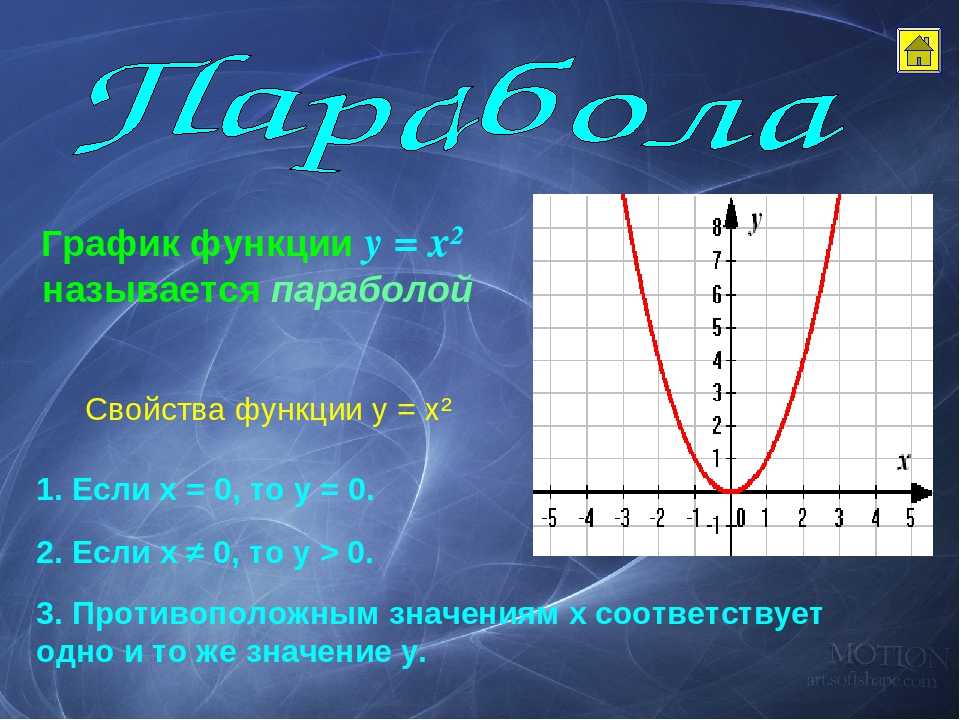
 Обоснование этого аналогично изложенному для случая, когда ка больше нуля.
Обоснование этого аналогично изложенному для случая, когда ка больше нуля.