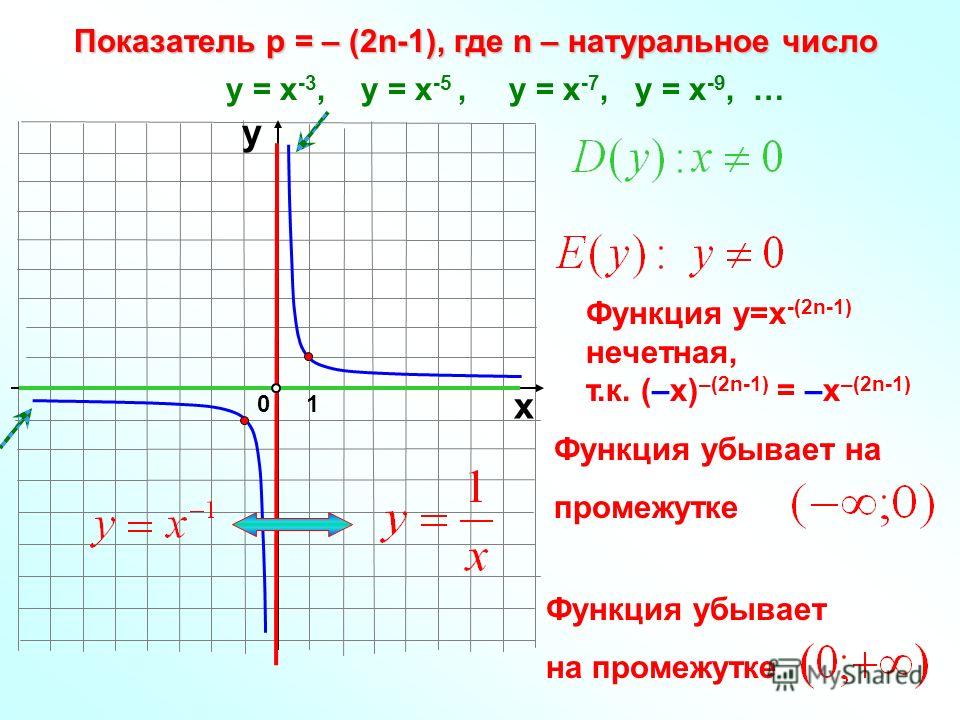
Y=1/x, 9 (девять) букв — Кроссворды и сканворды
Вопрос с кроссворда
Ответ на вопрос «Y=1/x «, 9 (девять) букв:
гипербола
Альтернативные вопросы в кроссвордах для слова гипербола
Троп, намеренное преувеличение
Кривая второго порядка; преувеличение
Геометрическая кривая
«Преувеличенная» геометрическая кривая
ж. математ. кривая линия, которая бы обозначилась на поверхности сахарной головы (конуса), если ее рассечь с боку, отвесно вдоль. Ритор. преувеличенье, всякое выражение впадающее в какую-либо крайность, напр. у меня нет ни копейки; он взором объемлет все. Гиперболический, принадлежащий к гиперболе, к ней относящийся. Гиперболоид математ. геометрическое тело, образуемое вращением гиперболы. Гиперстен м. черный камень с бронзовым отливом; павлит
«Реки крови» и «море слез» с точки зрения лингвиста
«реки крови» и «море слез» с точки зрения лингвиста
Определение слова гипербола в словарях
Википедия Значение слова в словаре Википедия
2a,$ причём ∣ F F ∣ > 2 a > 0.
Наряду с эллипсом и параболой , гипербола является коническим сечением и квадрикой . Гипербола может быть определена как коническое сечение с эксцентриситетом , бо́льшим единицы.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова. Значение слова в словаре Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
ж. Стилистический прием, заключающийся в чрезмерном преувеличении каких-л. качеств или свойств изображаемого предмета, явления и т.п. с целью усиления впечатления. разг. Любое чрезмерное преувеличение. ж. Незамкнутая кривая из двух ветвей, получаемая при …
Примеры употребления слова гипербола в литературе.
В таком случае, твои слова должно рассматривать как гиперболу, Автолик, — заявил Данай, — ибо эти два прекрасных маленьких создания вряд ли выскочили в полном вооружении из твоего лба, подобно Афине из головы Зевса.
И так как было совершенно ясно, что кара падет на одного из этих троих, Алкивиад с Никием сговорились и, объединив силы своих сторонников, обратили остракизм против самого Гипербола.
Кое-кто, правда, утверждает, будто Алкивиад договорился не с Никием, а с Феаком и Феаково содружество привлек на свою сторону, чтобы изгнать Гипербола, который отнюдь не ждал такой беды: ведь люди порочные и ничтожные никогда не подпадали этому наказанию, как совершенно справедливо заметил и комик Платон, говоря о Гиперболе: Хоть поделом он принял наказание, С его клеймом никак не совместить его: Суд черепков не для таких был выдуман.
Гипербола, градация, оксюморон, перифраз, алогизм, риторический вопрос, риторическое восклицание, но прежде всего — сравнение и метафора стали здесь объектом исследования.
Наряду с гиперболой и карикатурой Доманович часто обращается к приему контраста.
Еще и сейчас титулы их государей такие же фантастические гиперболы и преувеличения, как те титулы, которыми сыздавна религиозная лесть пыталась прославить богов.
Источник: библиотека Максима Мошкова
Линейные комбинации, линейная независимость
Дифференциальные уравнения второго порядка содержат вторую производную неизвестной функции (и, вполне возможно, также первую производную), но не производные более высокого порядка. Почти для каждого уравнения второго порядка, встречающегося на практике, общее решение будет содержать две произвольные константы, поэтому IVP второго порядка должно включать два начальных условия.
Даны две функции y 1 ( x ) и y 2 ( x ), любое выражение вида
, где c 1 и c 2 — константы, называется линейной комбинацией y 1 и 8 y являются частными линейными комбинациями y 1 и y 2 . Пример 1 : Is y = 2 x линейная комбинация функций y 6 Например, если
y 1 = e x и y 2 = x 2 9094, то0003
Итак, идея линейной комбинации двух функций такова: умножьте функции на любые желаемые константы; затем добавьте продукты.7 2
80045 2
?
Любое выражение, которое может быть записано в форме
представляет собой линейную комбинацию x и x 2 . Поскольку y = 2 x соответствует этой форме, если взять c 1 = 2 и c 2 = o, y = 2 x 9000 действительно является линейной комбинацией 6 x 9000 х 2 .
Пример 2 : Рассмотрим три функции y 1 = sin x, y 2 = cos x и y 3 = sin( x + 1). Покажите, что y 3 является линейной комбинацией y 1 и y 2 .
Формула сложения для функции с тех пор говорит
Обратите внимание, что это соответствует форме линейной комбинации sin x и cos x ,
, взяв c 1 = cos 1 и c 2 = sin 1.
Пример 3 : Можно ли быть написано функция y = x 3 . ?
Если бы ответ был да, то были бы константы c 1 и c 2 такое, что уравнение
справедливо для всех значений x . Полагая x = 1 в этом уравнении, мы получаем
и если х = -1 дает
Сложение последних двух уравнений дает 0 = 2 c 2 , поэтому c 2 = 0. общая линейная комбинация (*) сводится к
, что явно соответствует , а не для всех значений x .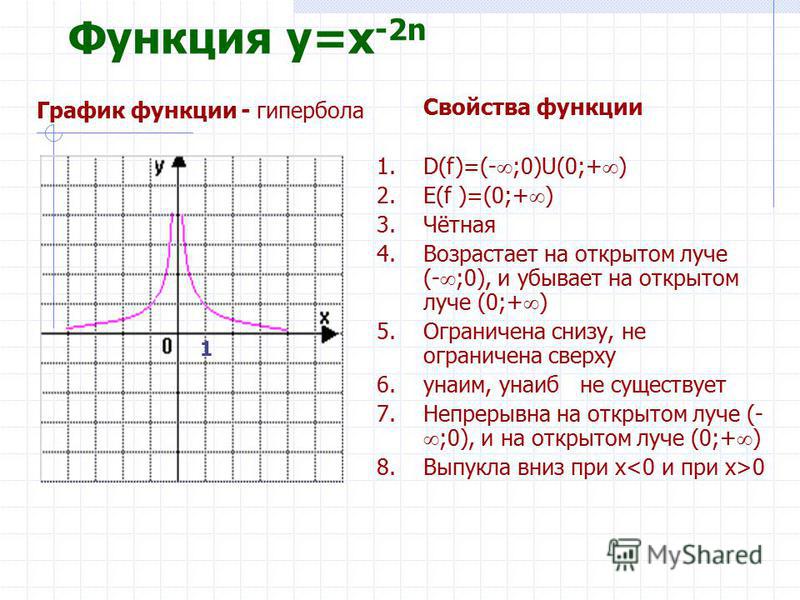
Еще одно определение: Две функции y 1 и y 2 называются линейно независимыми , если ни одна из функций не является постоянным кратным другой. Например, функции Y 1 = x 3 и Y 2 = 5 x 3 — Не Linearly Independent y 2 явно является константой, кратной y 1 . Проверить, что две функции зависимы, легко; проверка их независимости требует немного больше работы.
Пример 4
Если бы это было не так, то y 1 было бы постоянным кратным y 2
; то есть уравнение
будет выполняться для некоторых констант c и для всех x .
Но подставив x = π/2, например, дает абсурдное утверждение 1 = 0. Следовательно, приведенное выше уравнение не может быть истинным: y 1 = sin x равно , а не постоянному кратному y 2 = cos x ; таким образом, эти функции действительно линейно независимы.
Пример 5 : Функции y 1 = e x и y 2 = x линейно независимые?
Если бы это было не так, то y 1 было бы постоянным кратным y 2 ; то есть уравнение
будет выполняться для некоторых констант c и для всех x . Но этого не может быть, так как подстановка 
Пример 6 : Являются ли функции Y 1 = XE x и Y 2 = E x Linearly Independent?
Поспешным выводом может быть отказ, потому что y 1 кратно y 2 . Но y 1 не является константой , кратной y 2 , поэтому эти функции действительно независимы. (Вам может показаться поучительным доказать их независимость с помощью аргументов того же рода, что и в двух предыдущих примерах.) быть функцией.
Домен — это все действительные значения x, для которых определено y.
Если есть какое-либо значение x, для которого y не определено, мы должны исключить это конкретное значение из набора доменов.
Пример 1 :
Рассмотрим приведенную ниже рациональную функцию.
y = 1/(x — 2)
В приведенной выше рациональной функции приравняем знаменатель x — 2 к нулю.
x — 2 = 0
x = 2
В функции
y = 1/(x — 2),
, если x = 2, то знаменатель становится равным нулю, а значение ‘y’ становится неопределенным .
Таким образом, ‘y’ определено для всех действительных значений ‘x’, кроме x = 2.
Таким образом, домен равен
R — {2}
Диапазон рациональной функции
Пусть y = f (x) быть функцией.
Диапазон — это не что иное, как все действительные значения y для данного домена (действительные значения x).
Пример 2 :
Рассмотрим приведенную ниже рациональную функцию.
y = 1/(x — 2)
Чтобы найти диапазон приведенной выше рациональной функции, сначала мы должны найти обратную y.
Чтобы найти инверсию y, выполните шаги, указанные ниже.
Шаг 1 :
y = 1/(x — 2) определяется через y через x.
Та же самая функция должна быть переопределена x через y.
Шаг 2:
y = 1/(x — 2)
Умножьте каждую сторону на (x — 2).
(x — 2)y = 1
xy — 2y = 1
Добавьте 2y к каждой стороне.
xy = 2y + 1
Разделите каждую сторону на y.
х = (2г + 1) / г
Теперь функция определена x через y.
Шаг 3:
В x = (2y + 1) / y мы должны заменить x на y -1 и y на x.
Затем
y -1 = (2x + 1) / x
Шаг 4:
Теперь найдите домен y -1 .
Если в обратной функции y -1 заменить x на 0, знаменатель станет равным нулю, а значение y -1 станет неопределенным.
г -1 определяется для всех действительных значений x, кроме нуля.
Итак, домен y -1 равен
R — {0}
И мы уже знаем тот факт, что
Диапазон (y) = Домен (y -1 )
Следовательно, диапазон of y is
R — {0}
Другой способ найти диапазон рациональных функций
Для
некоторые рациональные функции, найти обратную функцию довольно сложно.
Таким образом, мы можем легко получить диапазон рациональных функций.
Давайте посмотрим, как найти диапазон рациональной функции, приведенной ниже.
y = 1/(x — 2)
Вертикальная асимптота :
Чтобы найти вертикальную асимптоту, мы должны сделать знаменатель (x — 2) равным нулю.
Когда мы это делаем,
x — 2 = 0
x = 2
Итак, вертикальная асимптота равна
x = 2
Горизонтальная асимптота0003
В рациональная функция y = 1 / (x — 2), старший показатель числителя меньше старшего показателя знаменателя.
Итак, есть горизонтальная асимптота.
Уравнение горизонтальной асимптоты:
y = 0
Таблица значений :
В данной рациональной функции y = 1/(x-2) теперь мы должны подставить некоторые случайные значения для x и найти соответствующие значения y.