Функция лапласа: 23. Функция Лапласа

Дифференциальное и интегральное исчисления для втузов, т.2

Дифференциальное и интегральное исчисления для втузов, т.2

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2: Учебное пособие для втузов.—13-е изд.— М.: Наука, Главная редакция физико-математической литературы, 1985. — 560 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Второй том включает разделы: дифференциальные уравнения, кратные и криволинейные интегралы, интегралы по поверхности, ряды, уравнения математической физики, операционное исчисление, элементы теории вероятностей и математической статистики, матрицы. Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА XIII. (n) = f(x) § 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31. Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки § 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 6. Замена переменных в двойном интеграле (общий случай) § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14. Момент инерции и координаты центра масс тела § 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13. Степенные ряды. Интервал сходимости § 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 23. Уравнение Бесселя § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4. Ряды Фурье для четных и нечетных функций § 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4. Уравнение распространения тепла в стержне. Формулировка краевой задачи § 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 7. Распространение тепла в неограниченном стержне § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. 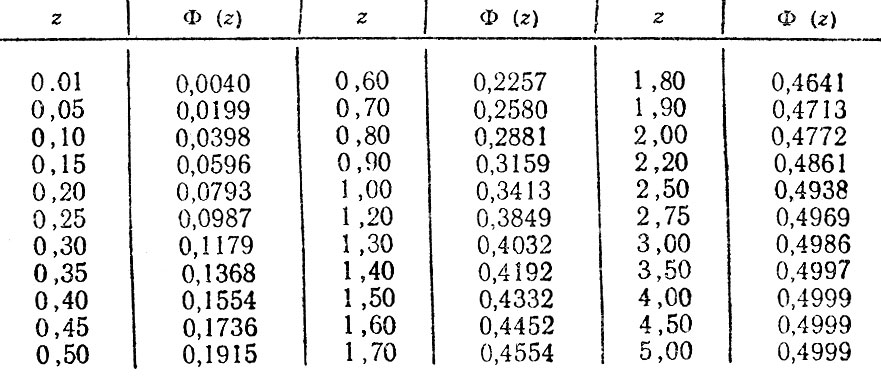Дифференцирование изображения § 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей § 2. Классическое определение вероятности и непосредственный подсчет вероятностей § 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15. Нормальный закон распределения. Математическое ожидание нормального распределения § 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 25. Вероятность попадания двумерной случайной величины в прямоугольник со сторонами, параллельными главным осям рассеивания, при нормальном законе распределения § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27. Задачи математической статистики. Статистический материал § 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13. Преобразование матрицы линейного преобразования при переходе от одного базиса к другому § 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ

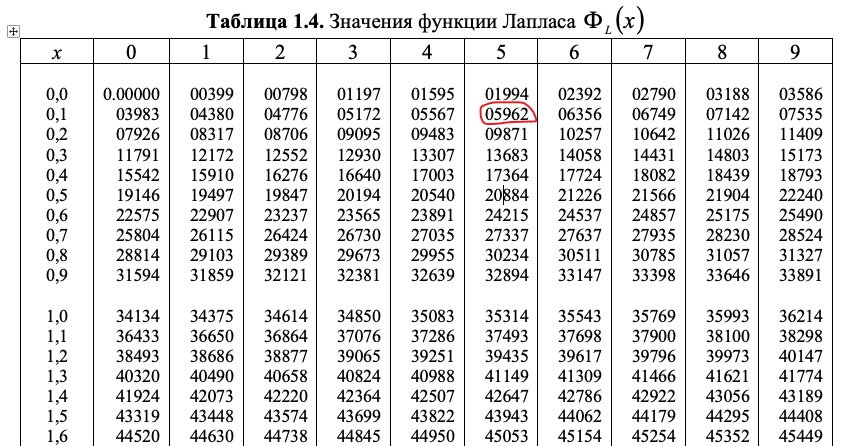
Таблица значений функции Лапласа

Таблица значений функции Лапласа

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00	0,00000	0,50	0,19146	1,00	0,34134	1,50	0,43319	2,00	0,47725	3,00	0,49865
0,01	0,00399	0,51	0,19497	1,01	0,34375	1,51	0,43448	2,02	0,47831	3,05	0,49886
0,02	0,00798	0,52	0,19847	1,02	0,34614	1,52	0,43574	2,04	0,47932	3,10	0,49903
0,03	0,01197	0,53	0,20194	1,03	0,34849	1,53	0,43699	2,06	0,48030	3,15	0,49918
0,04	0,01595	0,54	0,20540	1,04	0,35083	1,54	0,43822	2,08	0,48124	3,20	0,49931
0,05	0,01994	0,55	0,20884	1,05	0,35314	1,55	0,43943	2,10	0,48214	3,25	0,49942
0,06	0,02392	0,56	0,21226	1,06	0,35543	1,56	0,44062	2,12	0,48300	3,30	0,49952
0,07	0,02790	0,57	0,21566	1,07	0,35769	1,57	0,44179	2,14	0,48382	3,35	0,49960
0,08	0,03188	0,58	0,21904	1,08	0,35993	1,58	0,44295	2,16	0,48461	3,40	0,49966
0,09	0,03586	0,59	0,22240	1,09	0,36214	1,59	0,44408	2,18	0,48537	3,45	0,49972
0,10	0,03983	0,60	0,22575	1,10	0,36433	1,60	0,44520	2,20	0,48610	3,50	0,49977
0,11	0,04380	0,61	0,22907	1,11	0,36650	1,61	0,44630	2,22	0,48679	3,55	0,49981
0,12	0,04776	0,62	0,23237	1,12	0,36864	1,62	0,44738	2,24	0,48745	3,60	0,49984
0,13	0,05172	0,63	0,23565	1,13	0,37076	1,63	0,44845	2,26	0,48809	3,65	0,49987
0,14	0,05567	0,64	0,23891	1,14	0,37286	1,64	0,44950	2,28	0,48870	3,70	0,49989
0,15	0,05962	0,65	0,24215	1,15	0,37493	1,65	0,45053	2,30	0,48928	3,75	0,49991
0,16	0,06356	0,66	0,24537	1,16	0,37698	1,66	0,45154	2,32	0,48983	3,80	0,49993
0,17	0,06749	0,67	0,24857	1,17	0,37900	1,67	0,45254	2,34	0,49036	3,85	0,49994
0,18	0,07142	0,68	0,25175	1,18	0,38100	1,68	0,45352	2,36	0,49086	3,90	0,49995
0,19	0,07535	0,69	0,25490	1,19	0,38298	1,69	0,45449	2,38	0,49134	3,95	0,49996
0,20	0,07926	0,70	0,25804	1,20	0,38493	1,70	0,45543	2,40	0,49180	4,00	0,49997
0,21	0,08317	0,71	0,26115	1,21	0,38686	1,71	0,45637	2,42	0,49224	4,05	0,49997
0,22	0,08706	0,72	0,26424	1,22	0,38877	1,72	0,45728	2,44	0,49266	4,10	0,49998
0,23	0,09095	0,73	0,26730	1,23	0,39065	1,73	0,45818	2,46	0,49305	4,15	0,49998
0,24	0,09483	0,74	0,27035	1,24	0,39251	1,74	0,45907	2,48	0,49343	4,20	0,49999
0,25	0,09871	0,75	0,27337	1,25	0,39435	1,75	0,45994	2,50	0,49379	4,25	0,49999
0,26	0,10257	0,76	0,27637	1,26	0,39617	1,76	0,46080	2,52	0,49413	4,30	0,49999
0,27	0,10642	0,77	0,27935	1,27	0,39796	1,77	0,46164	2,54	0,49446	4,35	0,49999
0,28	0,11026	0,78	0,28230	1,28	0,39973	1,78	0,46246	2,56	0,49477	4,40	0,49999
0,29	0,11409	0,79	0,28524	1,29	0,40147	1,79	0,46327	2,58	0,49506	4,45	0,50000
0,30	0,11791	0,80	0,28814	1,30	0,40320	1,80	0,46407	2,60	0,49534	4,50	0,50000
0,31	0,12172	0,81	0,29103	1,31	0,40490	1,81	0,46485	2,62	0,49560	4,55	0,50000
0,32	0,12552	0,82	0,29389	1,32	0,40658	1,82	0,46562	2,64	0,49585	4,60	0,50000
0,33	0,12930	0,83	0,29673	1,33	0,40824	1,83	0,46638	2,66	0,49609	4,65	0,50000
0,34	0,13307	0,84	0,29955	1,34	0,40988	1,84	0,46712	2,68	0,49632	4,70	0,50000
0,35	0,13683	0,85	0,30234	1,35	0,41149	1,85	0,46784	2,70	0,49653	4,75	0,50000
0,36	0,14058	0,86	0,30511	1,36	0,41309	1,86	0,46856	2,72	0,49674	4,80	0,50000
0,37	0,14431	0,87	0,30785	1,37	0,41466	1,87	0,46926	2,74	0,49693	4,85	0,50000
0,38	0,14803	0,88	0,31057	1,38	0,41621	1,88	0,46995	2,76	0,49711	4,90	0,50000
0,39	0,15173	0,89	0,31327	1,39	0,41774	1,89	0,47062	2,78	0,49728	4,95	0,50000
0,40	0,15542	0,90	0,31594	1,40	0,41924	1,90	0,47128	2,80	0,49744	5,00	0,50000
0,41	0,15910	0,91	0,31859	1,41	0,42073	1,91	0,47193	2,82	0,49760
0,42	0,16276	0,92	0,32121	1,42	0,42220	1,92	0,47257	2,84	0,49774
0,43	0,16640	0,93	0,32381	1,43	0,42364	1,93	0,47320	2,86	0,49788
0,44	0,17003	0,94	0,32639	1,44	0,42507	1,94	0,47381	2,88	0,49801
0,45	0,17364	0,95	0,32894	1,45	0,42647	1,95	0,47441	2,90	0,49813
0,46	0,17724	0,96	0,33147	1,46	0,42785	1,96	0,47500	2,92	0,49825
0,47	0,18082	0,97	0,33398	1,47	0,42922	1,97	0,47558	2,94	0,49836
0,48	0,18439	0,98	0,33646	1,48	0,43056	1,98	0,47615	2,96	0,49846
0,49	0,18793	0,99	0,33891	1,49	0,43189	1,99	0,47670	2,98	0,49856

 

Дифференциальные уравнения — преобразования Лапласа

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

В этой главе мы рассмотрим, как использовать преобразования Лапласа для решения дифференциальных уравнений. В мире существует множество видов трансформаций. Лаплас преобразования и преобразования Фурье, вероятно, являются двумя основными типами используемых преобразований. Как мы увидим в следующих разделах, мы можем использовать преобразования Лапласа, чтобы свести дифференциальное уравнение к алгебраической задаче. Иногда алгебра может быть запутанной, но во многих случаях это будет проще, чем непосредственное решение дифференциального уравнения. Лаплас преобразования также можно использовать для решения IVP, для которых мы не можем использовать какой-либо предыдущий метод.

Для «простых» дифференциальных уравнений, подобных приведенным в первых нескольких разделах последней главы, преобразования Лапласа будут более сложными, чем нам нужно. На самом деле, для большинства однородных дифференциальных уравнений, подобных приведенным в предыдущей главе, преобразования Лапласа значительно длиннее и не так полезны. Кроме того, многие из «простых» неоднородных дифференциальных уравнений, которые мы видели в «Неопределенных коэффициентах и ​​вариациях параметров», по-прежнему проще (или, по крайней мере, не сложнее, чем преобразования Лапласа) в том виде, в каком мы их делали там. Однако на данный момент объем работы, необходимый для преобразования Лапласа, начинает равняться объему работы, который мы проделали в этих разделах.

Преобразование Лапласа вступает в свои права, когда вынуждающая функция в дифференциальном уравнении начинает усложняться. В предыдущей главе мы рассматривали только неоднородные дифференциальные уравнения, в которых \(g(t)\) — довольно простая непрерывная функция. В этой главе мы начнем рассматривать \(g(t)\), которые не являются непрерывными. Именно в этих проблемах начинают проясняться причины использования преобразований Лапласа.

Мы также увидим, что для некоторых более сложных неоднородных дифференциальных уравнений из предыдущей главы Лаплас преобразования на самом деле легче решают эти проблемы.

Вот краткое изложение разделов этой главы.

Определение. В этом разделе мы даем определение преобразования Лапласа. Мы также вычислим пару преобразований Лапласа, используя определение.

Преобразования Лапласа. В этом разделе мы познакомим вас с тем, как мы обычно вычисляем преобразования Лапласа, что позволяет избежать необходимости использовать определение. Мы обсудим таблицу преобразований Лапласа, использованную в этом материале, и проработаем множество примеров, иллюстрирующих использование таблицы преобразований Лапласа.

Обратные преобразования Лапласа. В этом разделе мы задаем вопрос, противоположный предыдущему. Другими словами, учитывая преобразование Лапласа, какая функция у нас изначально была? Мы снова работаем с множеством примеров, иллюстрирующих, как использовать таблицу преобразований Лапласа для этого, а также некоторые манипуляции с данным преобразованием Лапласа, необходимые для использования таблицы.

Ступенчатые функции. В этом разделе мы познакомимся со ступенчатой ​​функцией или функцией Хевисайда. Мы проиллюстрируем, как записать кусочную функцию в терминах функций Хевисайда. Мы также работаем с множеством примеров, показывающих, как использовать преобразования Лапласа и обратные преобразования Лапласа, которые включают функции Хевисайда. Мы также выводим формулы преобразования Лапласа функций, включающих функции Хевисайда.

Решение IVP с помощью преобразований Лапласа. В этом разделе мы рассмотрим, как использовать преобразования Лапласа для решения IVP. Примеры в этом разделе ограничены дифференциальными уравнениями, которые можно решить без использования преобразования Лапласа. Преимущество начала с этого типа дифференциального уравнения состоит в том, что работа, как правило, не такая сложная, и мы всегда можем проверить свои ответы, если захотим.

IVP с непостоянными коэффициентами. В этом разделе мы дадим краткий обзор использования преобразований Лапласа для решения IVP с непостоянными коэффициентами. Мы не работаем с большим количеством примеров в этом разделе. Мы работаем только с парой, чтобы проиллюстрировать, как работает процесс с преобразованиями Лапласа.

IVP со ступенчатыми функциями — это раздел, в котором причина использования преобразований Лапласа действительно становится очевидной. Мы будем использовать преобразования Лапласа для решения IVP, которые содержат функции Хевисайда (или ступенчатые). Без преобразований Лапласа их решение потребовало бы немало работы. Хотя мы работаем с одним из этих примеров без преобразований Лапласа, мы делаем это только для того, чтобы показать, что было бы, если бы мы попытались решить один из примеров без использования преобразований Лапласа.

Дельта-функция Дирака. В этом разделе мы вводим дельта-функцию Дирака и получаем преобразование Лапласа дельта-функции Дирака. Мы работаем с парой примеров решения дифференциальных уравнений с использованием дельта-функций Дирака, и, в отличие от задач с функциями Хевисайда, наш единственный реальный вариант для такого рода дифференциальных уравнений — использовать преобразования Лапласа. Мы также даем хорошее соотношение между дельта-функциями Хевисайда и Дирака.

Интеграл свертки. В этом разделе мы даем краткое введение в интеграл свертки и то, как его можно использовать для выполнения обратных преобразований Лапласа. Мы также проиллюстрируем его использование при решении дифференциального уравнения, в котором вынуждающая функция (, т.е. член без каких-либо y в нем) неизвестна.

Таблица преобразований Лапласа. Этот раздел представляет собой таблицу преобразований Лапласа, которую мы будем использовать в материале. Мы даем как можно более широкий спектр преобразований Лапласа, включая те, которые не часто приводятся в таблицах преобразований Лапласа.

Передаточные функции модели с применением преобразования Лапласа в LTspice

Аннотация

Передаточные функции используются при разработке электронных систем, таких как фильтры, блоки питания и другие системы управления. Анализ в частотной области передаточной функции включает преобразование Лапласа. В этой статье исследуется реализация передаточной функции в LTspice ^® , сравнивает идеальную ответ на смоделированную реализацию и предоставляет несколько полезных примеров по пути. Файлы доступны для помощи в понимании и реализации этой темы.

Введение

Передаточные функции используются, когда мы хотим проанализировать, как выход системы меняется в зависимости от ввода. Система может быть выходным напряжением Резисторный делитель или скорость автомобиля при нажатии на газ. Чтобы проанализировать систему, мы хотим знать, как его выходная амплитуда и фаза сравниваются с входным сигналом. частота. Для этого воспользуемся преобразованием Лапласа.

Существует множество ресурсов, посвященных как математике, так и интуиция преобразования Лапласа. Для наших целей мы можем рассматривать его как математический инструмент, который позволяет нам работать с усилением, частотой, фазой и экспоненциальный отклик системы.

Основная идея диаграммы передаточной функции показана на рисунке 1.

Рис. 1. Передаточная функция.

Рис. 2. Резистивный делитель и RC-цепочка уменьшают амплитуду вдвое при f = 1 кГц. RC-цепь также вносит задержку.

На рис. 2 показаны две разные передаточные функции. Резисторный делитель просто описывается как:

Но RC-цепь описывается немного более сложным уравнением 2:

Запись передаточной функции в таком виде позволяет нам говорить о полюсах и нулях. Здесь мы имеем один полюс при ωp = 1/RC. В то время как выход 1 кГц RC-цепи (красная кривая) имеет ту же амплитуду, что и резистивный делитель, фазовая задержка заметна. Преобразование Лапласа позволяет нам описать, как RC-цепь изменяет как усиление, так и и фаза по частоте. Пример файла Simple_RC_vs_R_Divider.asc. ¹

Синтаксис преобразования Лапласа в LTspice

Чтобы реализовать преобразование Лапласа в LTspice, сначала поместите зависящее от напряжения источник напряжения в вашей схеме. Диалоговое окно для этого показано на рисунке 3.

Рис. 3. Размещение источника напряжения, зависящего от напряжения.

Щелкните правой кнопкой мыши элемент источника напряжения, чтобы открыть его Редактор атрибутов компонентов . В поле Value введите «Laplace = », а затем ваше уравнение, которое должно содержат комплексную переменную «s».

Поле значения» data-class=»img-responsive»>

Рисунок 4. Введите уравнение в поле Value .

На рисунке 4 {C} и {R} заключены в фигурные скобки, чтобы мы могли использовать .step spice для циклического переключения некоторых значений.

Моделирование на рис. 5 показывает переходную характеристику делителя импеданса RC, и эквивалентная передаточная функция, записанная с использованием преобразования Лапласа. Запуск Simulation, ² мы видим, что два выхода совпадают.

Рис. 5. Простая RC-цепь и эквивалентное ей преобразование Лапласа.

Поскольку передаточные функции становятся больше, я счел полезным использовать код редактор, который автоматически выделяет совпадающие скобки. Введите уравнение в текстовом редакторе, а затем скопируйте его в диалоговое окно LTspice. См. рис. 6.

Рисунок 6. Использование подсветки синтаксиса в текстовом редакторе.

Повторный курс по полюсам и нулям

Пример передаточной функции приведен в уравнении 3.

Анализируя уравнение 3, мы сначала видим член ω _р0 /с. Это называется происхождением полюс. Исходный полюс является синонимом интегратора и используется для обеспечения высокий коэффициент усиления на низких частотах, что исключает установившуюся ошибку в системе управления. Исходные полюса приводят к постоянной фазовой задержке 90° и характеристике усиления –20 дБ на десятилетие. Термин ω _p0 относится к частоте, при которой усиление, связанное с исходным полюсом, упал до 0 дБ.

Нахождение корней числителя и знаменателя дает нам ноль и полюс частот соответственно. Обратите внимание, что частоты полюсов/нулей задаются величина (то есть абсолютная величина) этих корней. Ноль приводит к увеличению фазы из 90° и увеличение усиления вокруг его частоты. Полюс приводит к фазе задержка на 90° и уменьшение усиления вокруг его частоты.

Если вместо примера передаточная функция была записана как:

Начальный член «s» теперь обозначается нулем в начале координат. Нуль в начале координат представитель чистого дифференциатора. Он имеет постоянный фазовый подъем 90 ° и его усиление увеличивается с частотой, достигая усиления 0 дБ на частоте ω _z0 .

На рис. 7 показан пример реализации этих различных полюсов и нулей. в отдельности. Каждый имеет частоту 1 кГц. Результирующее усиление и фаза каждого показан на рис. 8. Файл примера — PoleZeroExamples.asc. ³

Рисунок 7. Реализация полюсов и нулей.

Рис. 8. Частотная и фазовая характеристики полюсов и нулей, все на частоте 1 кГц.

Сравнение идеальной и смоделированной реализации

Используя LTspice для моделирования передаточной функции, вы можете воспользоваться обширная библиотека смоделированных компонентов. В качестве первого примера рассмотрим инвертирование операционный усилитель, обеспечивающий пропорциональное усиление. В идеале H(s) = –R _p /R _i . Это должно привести в простом масштабировании входного напряжения и фазовом сдвиге на 180°. Но как показано на рисунке 9, примерно на 320 кГц усиление отклоняется от идеала на 3 дБ и фаза сильно сдвинулась. Это следует из ширины полосы усиления LT6015 — 3,2 МГц, а схема на рис. 9 имеет коэффициент усиления —10 В/В.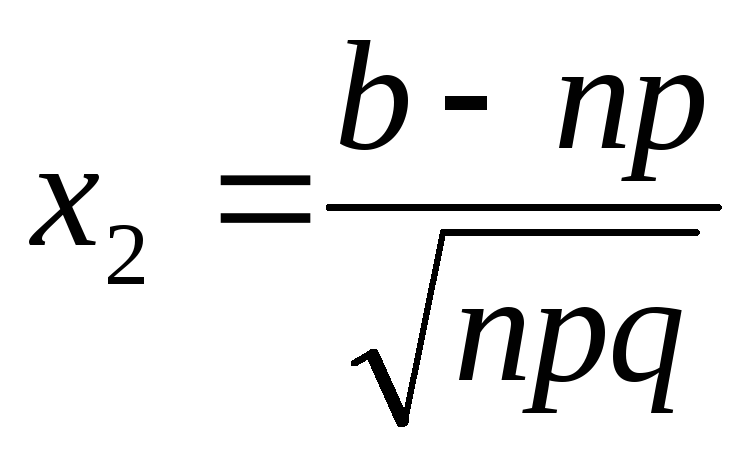

Рис. 9. Пропорциональное усиление.

В LTspice можно вводить собственные уравнения в средство просмотра сигналов. Если мы хотим увидеть усиление и разность фаз между нашим идеальным уравнением и схема на основе операционного усилителя, затем мы добавляем новую форму волны. Делается это правой кнопкой мыши в средстве просмотра сигнала и выбрав Добавить следы . Тогда выражение может быть добавлено для построения графика деления одного узла на другой (то есть V(vout_pro)/V(vout_laplace)). См. рис. 10.

Рис. 10. Добавление расчетной формы волны.

Сравнение усиления и фазы показано на рис. 11, что упрощает видим, что на низких частотах у нас разница в усилении 0 дБ и расхождения нет в фазе. Файл примера — ProportionalGain.asc. ⁴

Рис. 11. Сравнение усиления и фазы двух сигналов.

Система RLC второго порядка

Общая форма системы второго порядка дана Саймоном Брамблом. статья «Электронная теория управления системами второго порядка: практический анализ для инженеров».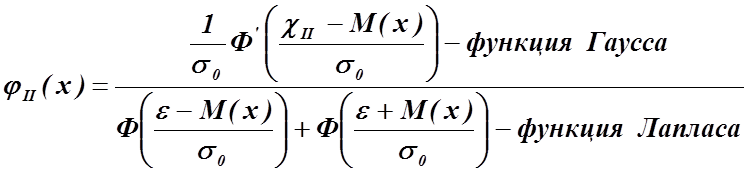 ⁵

При реализации в виде LRC мы имеем

Реализация LTspice показана на рисунке 12. Пример позволяет вам укажите R, L и C, или, в качестве альтернативы, вы можете указать коэффициент демпфирования ζ и резонансная частота ω _и .

Рис. 12. Система RLC второго порядка.

Частотная характеристика этой системы второго порядка показана на рисунке 13. показанный пик часто нежелателен, требует демпфирования при проектировании чего-либо как входной фильтр электромагнитных помех для понижающего регулятора. Файл примера — LRC_AC_Analysis.asc. ⁶

Рис. 13. Частотная характеристика RLC.

Дифференциатор и шест безопасности

Дифференциатор показан на рис. 14.

Рисунок 14. Дифференциатор.

Как и ожидалось, начало нуля приводит к увеличению усиления по частоте на 20 дБ/декаду. Дифференциаторы используются для увеличения отклика на высокочастотные сигналы. На практике чистые дифференциаторы не используются, а реализуются с помощью добавление страховочного столба. Столб безопасности размещается таким образом, чтобы система не была чрезмерно чувствителен к высокочастотному шуму. Также обратите внимание на резонансный пик, показанный на реализация ОУ. Этот пик может оказаться проблематичным при попытке контролировать систему.

Реализация, показанная на рис. 14, имеет ноль (где коэффициент усиления пересекает 0 дБ) на уровне

.

В нашем примере шест безопасности реализован в пять раз больше этого значения. Рисунок 15 показывает дифференциатор плюс реализацию полюса безопасности. Полюсная частота мы хотим, 5 × 159 Гц = 796 Гц. Для этого поместим конденсатор обратной связи с 1/5 номинала входного конденсатора. Полная передаточная функция задается числом

.

, где ω _z = 1/R _p C _d и ω _p = 1/R _p C _i . Моделирование (см. рисунок 11) показывает нам, что это полюс безопасности уменьшает как усиление, так и фазу по мере приближения к частоте полюса.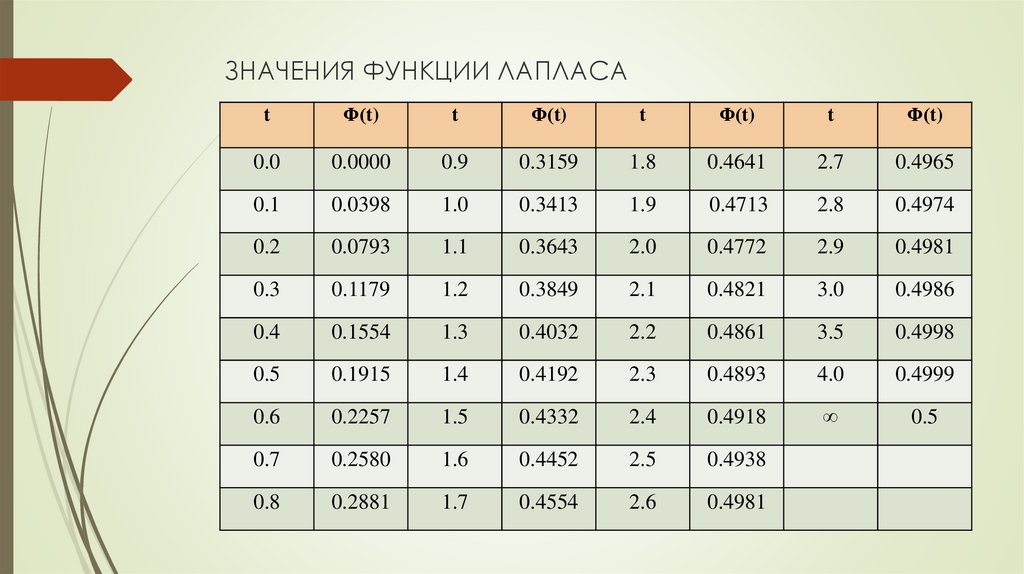 Выбросы из-за операционного усилителя также уменьшаются.

Задержка первого порядка плюс (FOPD)

При моделировании поведения системы полезным инструментом является модель FOPD. Для более полное объяснение читайте в лекции доктора Джона Д. Хеденгрена «Моделирование динамических процессов». ⁷ Короче говоря, процесс можно описать фиксированной задержкой, полномасштабный отклик и постоянная времени. Для реализации фиксированной задержки возьмем преимущество следующего преобразования Лапласа:

Напоминаем, что постоянная времени определяется как 1 –1/e = 63,2%. Модель FOPD выходит как:

с

k _p = полный выход

𝜏 _F = постоянная времени

𝛳 _F = время задержки

На рис. 16 показана реализация системы с полной шкалой 100, постоянная времени 10 с и задержка 1 с. Поскольку входной шаг применяется при t = 1 с, из рисунка 17 следует, что при t = 12 с выходное напряжение составляет 63,2 В. Файл моделирования это FOPD.asc. ⁸

Рисунок 16. Модель первого порядка плюс задержка.

Рисунок 17. Реакция первого порядка плюс задержка на шаг ввода.

Дизайн компенсатора в LTspice

Проектирование систем управления — обширная область, охватывающая множество дисциплин. Ключевой компонент к замкнутой системе управления является компенсатором. Как только передаточная функция управляемая система известна, компенсатор предназначен для устранения усиления и регулировка фазы, необходимая для стабильности и производительности с обратной связью.

Компенсатор ПИ (тип 2а)

Многие системы можно компенсировать с помощью компенсатора типа 2а, состоящего из полюса в начале координат (интегратор) плюс ноль. Отрицательная обратная связь обеспечивает 180° фазовая задержка, в то время как полюс в начале координат приводит к еще одной фиксированной задержке в 90°. К установка нуля означает, что дополнительный фазовый сдвиг на 90 ° удаляется на более высоких частотах. При таком подходе мы можем решить, какой фазовый сдвиг мы хотим получить в конкретном случае. частоту и поставьте нуль соответственно.

Рис. 18. Компенсатор на основе операционного усилителя типа 2а.

Контроллер типа 2а на основе операционного усилителя показан на рис. 18. Трансформатор типа 2а функция записывается как

Частота исходного полюса определяется как ω _p = 1/R ₂ C _i , а нулевая частота равна ω _z = 1/R ₂ C _i .

Влияние операционного усилителя здесь снова проявляется как в усилении, так и в сдвиге фазы. от идеала на более высоких частотах. Файл примера — Type2a.asc. ⁹

Компенсатор типа 2

Компенсатор типа 2 состоит из исходного полюса и пары полюс/ноль и принимает форма, показанная на рисунке 19.

Рис. 19. Компенсатор типа 2.

Передаточная функция определяется как:

С расположением полюсов/нулей:

 

В этот момент дизайнер сталкивается с дилеммой.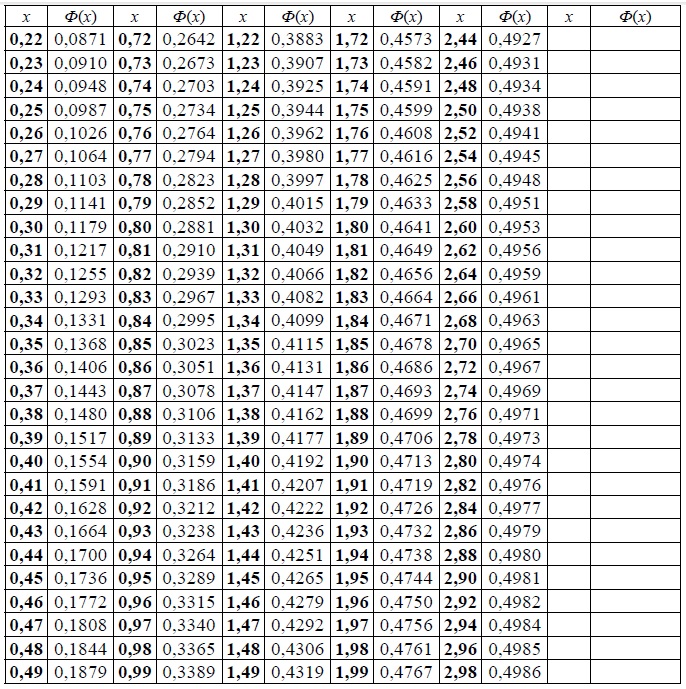 Выбор Rs и Cs влияет на оба полюс и ноль. Кроме того, вопрос о том, где разместить полюс и ноль, необходимо решить. быть адресовано. Книга Проектирование контуров управления для линейной и импульсной мощности Расходные материалы выводит и дает пример пошагового выполнения процесса проектирования. Чтобы помочь читателю, этот метод применяется и приводится в файле примера LTspice, Type2_autoCalcs.asc. ¹⁰ Результат этого примера показан на рис. 20. Цель достигается ослабление на 10 дБ с усилением фазы на 30° на частоте 10 кГц. Еще раз, неидеальные свойства ОУ проявляются на более высоких частотах.

Рис. 20. Фазовая и частотная характеристики типа 2.

Компенсатор типа 3

Компенсатор типа 3 имеет форму, показанную на рис. 21.

Рис. 21. Компенсатор типа 3.

Мотивация для этой более сложной передаточной функции заключается в том, что мы можем получить доступ к большему фазовому наддуву. Отрицательная обратная связь дает нам первоначальный разворот на 180°. задерживать. Но теперь у нас есть доступ к двум нулям, которые могут повысить фазы на 180°. Два полюса размещены для спада высокочастотного усиления и фазы. Передаточная функция определяется выражением:

С расположением полюсов/нулей:

Как и в случае с компенсатором типа 2а, процесс выбора положения полюса/нуля а затем выполняется расчет Rs и Cs. Книга Проектирование контуров управления для линейных и импульсных источников питания выводит и дает пример того, как пройти через процесс проектирования. В помощь читателю этот метод применяется и приведен в файле примера LTspice Type3_autoCalcs.asc.. ¹¹ Вывод этого пример показан на рис. 22. Целью является ослабление на 10 дБ с фазой 145°. достигается усиление на частоте 5 кГц. Еще раз о неидеальных свойствах ОУ проявляются на более высоких частотах.

Рис. 22. Отклик компенсатора типа 3.

Исходный полюс во временной области

До этого момента мы показали, как LTspice может реализовать передаточную функцию, с помощью элементов схемы и преобразования Лапласа. Показанные примеры были в частотная область. Естественно следовать анализу этих передаточных функций. во временной области (то есть ступенчатая характеристика).

Для этого нам нужно решить вопрос с исходным полюсом и как реализовать это. Передаточная функция с исходным полюсом (то есть чистый интегратор) равна H(s) = 1/s. Этот передаточная функция прекрасно работает в частотной области (рис. 23), но во временной домен мы получаем ошибку (рисунок 24).

Рис. 23. Анализ переменного тока исходного полюса.

Рис. 24. Не удалось выполнить анализ переходных процессов исходного полюса.

Чтобы решить эту проблему, мы можем вместо этого использовать поведенческий источник напряжения и Функция ID(). Этот подход показан на Рисунке 25. На Рисунке 25 также начало системы обратной связи, которая сравнивает неудачу со статической обратной связью Напряжение. Файл примера — OriginPole_TransientAnalysis_idt.asc. ¹²

Рисунок 25. Интеграция, работающая во временной области.

Конструкция фильтра

Справочник по проектированию линейных цепей ¹³ — это лишь часть обширной библиотеки учебных пособий. материалы предоставлены Analog Devices. В главе 8 обсуждаются аналоговые фильтры. Представление Лапласа фильтров, обсуждаемых в этой главе, дано в виде пример файла Laplace_Filters_LinearSystemsBook.asc. ¹⁴ Обратитесь к разделу проектирования фильтров Precision Toolbox, который помогает в разработке активных фильтров. ¹⁵

Заключение

Было приведено множество примеров того, как реализовать передаточную функцию. путем сравнения представления сосредоточенных элементов с представлением на основе преобразования Лапласа уравнение. Эти примеры носят образовательный характер в смысле подключения классной комнаты. теории для реализации схемы, и они помогают в практическом проектировании различных компенсаторы. Важно отметить, что для импульсных источников питания LTpowerCAD — это мощный (и предпочтительный) ресурс для расчета компенсации.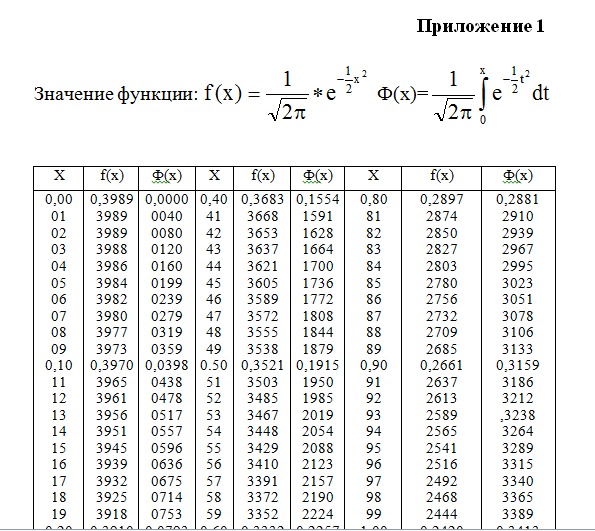 ¹⁶ Хотя LTspice можно использовать для работы и понимания некоторых компенсаторов, в в случае проектирования источников питания LTPowerCAD является подходящим инструментом для этой работы.

Рекомендации

¹ Simple_RC_vs_R_Divider.asc. Аналоговые устройства, Inc.

² Laplace_Simple_RC.asc. Аналоговые устройства, Inc.

³ PoleZeroExamples.asc. Аналоговые устройства, Inc.

⁴ ProportionalGain.asc. Аналоговые устройства, Inc.

⁵ Саймон Брамбл. «Теория электронного управления системами второго порядка: практический Анализ для инженеров». Аналоговый диалог, Vol. 54, № 3, сентябрь 2020 г.

⁶ LRC_AC_Analysis.asc. Аналоговые устройства, Inc.

⁷ Джон Д. Хеденгрен. «Динамическое моделирование процессов».

⁸ FOPD.asc. Аналоговые устройства, Inc.

⁹ Type2a.