НОУ ИНТУИТ | Лекция | Случайные события, случайные величины. Их законы распределения и числовые характеристики
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >
Аннотация: В лекции рассмотрены случайные величины и события, методы их генерации и область их применения.
Ключевые слова: значение, дискретная случайная величина, вероятность, биномиальное распределение, Распределение Бернулли, Распределение Пуассона, функция, случайная величина, график, первообразная, предел, определение, ПО, нормальное распределение, имитационное моделирование, постоянное значение, определенный интеграл, интервал, дисперсия, разность, математическим ожиданием, среднеквадратичное отклонение, место, нормальный закон, вес, асимптота, ордината, площадь, выражение
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначим: X, Y, Z – случайные величины
xi, yi, zi – возможные значения случайных величин.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения или с определенными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно
Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически (в виде многоугольника распределения).
Закон распределения можно задать таблично, аналитически (в виде формулы) и графически (в виде многоугольника распределения).
Табличное задание закона распределения:
возможные значения случайной величины;
вероятности появления случайной величины.
Аналитическое задание закона распределения:
Биномиальное распределение, определяемое распределением Бернуллиk = 0, 1, 2, …, n – количество возможных появлений событий
q = 1-p – вероятность не появления событий.
Распределение Пуассона, определяемое асимптотической формулой Пуассона:
где:
intuit.ru/2010/edi»> — интенсивность потока событий.Графическое задание закона распределения представлено на рис.6.1.
Рис. 6.1.
Способ описания распределения случайной величины в виде таблицы, в виде формулы или графически применим только для дискретных случайных величин.
Интегральная функция распределения позволяет задать как дискретную, так и непрерывную случайную величину.
Интегральная функция распределения (ИФР)– это функция F(x), определяющая для каждого возможного значения x вероятность того, что случайная величина X примет значение меньшее x, т. е.
Геометрический смысл интегральной функции распределения – это вероятность того, что случайная величина X примет значение, которое на числовой оси лежит левее точки x.
Свойства интегральной функции распределения:
- Значения интегральной функции распределения принадлежат отрезку [0;1]: ..
- Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b), равна приращению интегральной функции распределения на этом интервале
- Если все возможные значения x случайной величины принадлежат интервалу (a, b), то
, если ,
, если .
График ИФР непрерывной случайной величины представлен на рис. 6.2
Рис. 6.2. График ИФР непрерывной случайной величины
График ИФР дискретной случайной величины представлен на рис. 6.3
Рис. 6.3. График ИФР дискретной случайной величины
6.3. График ИФР дискретной случайной величины
Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.
Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.
Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:
Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью x, кривой распределения f(x) и прямыми x = a и x = b (рис.
Рис. 6.4.
График дифференциальной функции распределения принято называть кривой распределения.
Дальше >>
< Лекция 5 || Лекция 6: 12345 || Лекция 7 >
17. Непрерывные случайные величины. Функция распределения вероятности непрерывной случайной величины, ее свойства и график.
Функцией распределения вероятностей называют функцию , определяющую вероятность того, что случайная величина х в результате испытания примет значение, меньшее х, то есть: . Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
1. Значения
функции распределения вероятностей
принадлежат отрезку
[0,1]:. 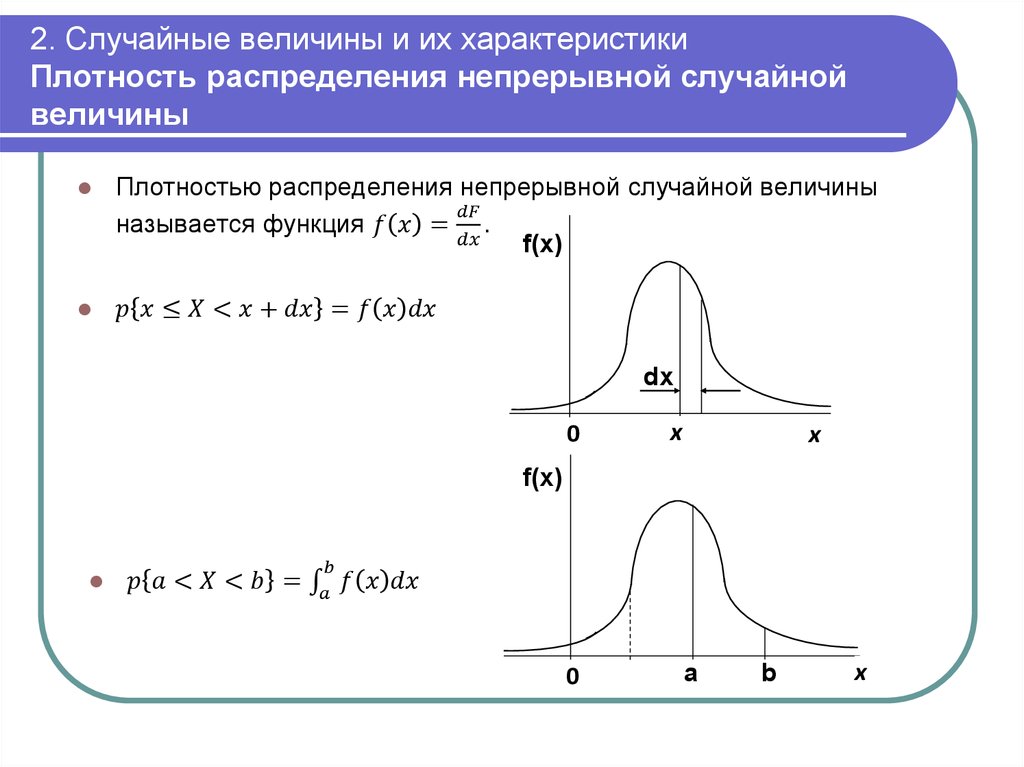 Следствие
1. Вероятность
того, что случайная величина примет
значение, заключенное в интервале (a,b),
равна приращению функции распределения
вероятностей на этом интервале: . Следствие
2. Вероятность
того, что непрерывная случайная величина
примет одно определенное значение,
равна нулю.
Используя последнее
следствие, легко убедиться в справедливости
следующих равенств: . 3. Если
возможные значения непрерывной случайной
величины принадлежат интервалу (a,b),
то: ,
если
; ,
если
. Следствие. Если
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения: 18.
Функция распределения плотности
вероятностей непрерывной случайной
величины, ее числовые характеристики
мат. ожидание, дисперсия, среднее
квадратичное отклонение.
Следствие
1. Вероятность
того, что случайная величина примет
значение, заключенное в интервале (a,b),
равна приращению функции распределения
вероятностей на этом интервале: . Следствие
2. Вероятность
того, что непрерывная случайная величина
примет одно определенное значение,
равна нулю.
Используя последнее
следствие, легко убедиться в справедливости
следующих равенств: . 3. Если
возможные значения непрерывной случайной
величины принадлежат интервалу (a,b),
то: ,
если
; ,
если
. Следствие. Если
возможные значения непрерывной случайной
величины расположены на всей числовой
оси, то справедливы следующие предельные
соотношения: 18.
Функция распределения плотности
вероятностей непрерывной случайной
величины, ее числовые характеристики
мат. ожидание, дисперсия, среднее
квадратичное отклонение.
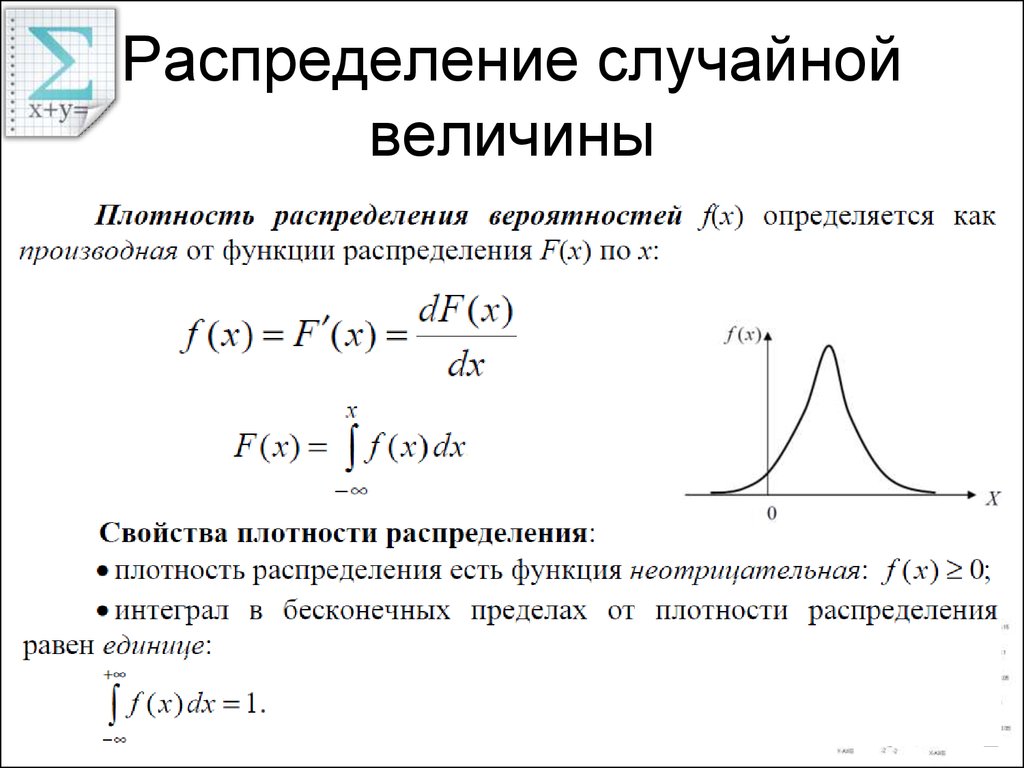
Плотностью
распределения вероятностей непрерывной
случайной величины называют
функцию
–
первую производную от функции
распределения вероятностей
:
Таким
образом, функция распределения
вероятностей является первообразной
для плотности распределения
вероятностей. Теорема. Вероятность
того, что непрерывная случайная
величина х примет
значение, принадлежащее интервалу (a,b),
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Следовательно,
зная плотность распределения
вероятности
,
можно найти функцию распределения
по
формуле
.
Теорема. Вероятность
того, что непрерывная случайная
величина х примет
значение, принадлежащее интервалу (a,b),
равна определенному интегралу от
плотности распределения, взятому в
соответствующих пределах:
.
Следовательно,
зная плотность распределения
вероятности
,
можно найти функцию распределения
по
формуле
.
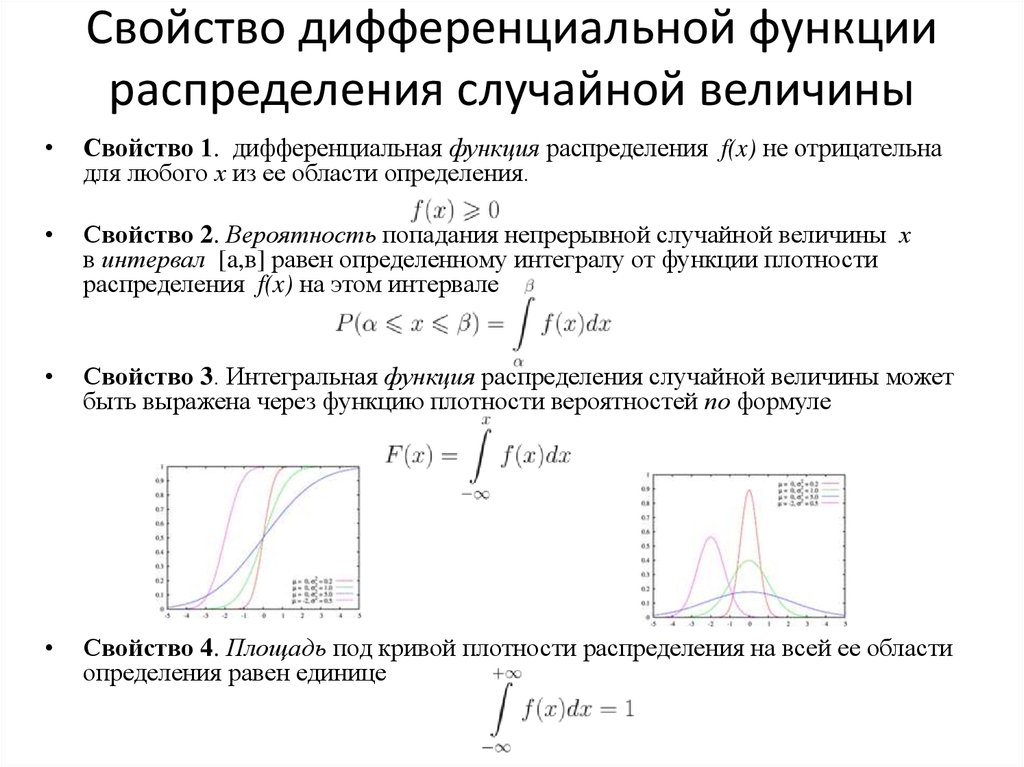
Свойства плотности распределения вероятностей
1. Плотность распределения вероятностей – неотрицательная функция:
2. Несобственный интеграл от плотности распределения вероятностей в пределах всей числовой оси равен единице: .
Математическим
ожиданием непрерывной случайной
величины х,
возможные значения которой принадлежат
отрезку [a,b],
называют определенный интеграл
.
Если
возможные значения принадлежат всей
числовой оси, то интеграл от –беск-ти
до + беск-ти Дисперсией
непрерывной случайной величины называют
математическое ожидание квадрата ее
отклонения.
Если возможные непрерывной
случайной величины х принадлежат
отрезку [a,b],
то
. Средним
квадратическим отклонением непрерывной
случайной величины называют,
как и для величины дискретной, квадратный
корень из дисперсии.
Средним
квадратическим отклонением непрерывной
случайной величины называют,
как и для величины дискретной, квадратный
корень из дисперсии.
14.2 — Совокупные функции распределения
Возможно, вы помните, что кумулятивная функция распределения определяется для дискретных случайных величин следующим образом:
\(F(x)=P(X\leq x)=\sum\limits_{t \leq x} f(t)\)
Опять же, \(F(x)\) накапливает все вероятности, меньшие или равные \(x\). Кумулятивная функция распределения для непрерывных случайных величин является просто прямым расширением функции дискретного случая. Все, что нам нужно сделать, это заменить суммирование интегралом. 9х f(t)dt\)
для \(-\infty Вы, наверное, помните, что для дискретных случайных величин \(F(x)\) является, вообще говоря, неубывающей функцией, состоящей из шагов и . Для непрерывных случайных величин \(F(x)\) является неубывающей непрерывной функцией. Вернемся к примеру, в котором \(X\) имеет следующую функцию плотности вероятности: 93}{4}\) для \(0 Предположим, что p.d.f. непрерывной случайной величины \(X\) определяется как: \(f(x)=\begin{cases} x+1, & -1 Найдите и постройте график c.d.f. \(F(x)\). Если мы посмотрим на график p.d.f. \(f(x)\): мы видим, что кумулятивная функция распределения \(F(x)\) должна быть определена на четырех интервалах — для \(x\le — 1\), когда \(-1 Таким образом, кумулятивная функция распределения представляет собой вогнутую вверх параболу на интервале \(-1 Для любой случайной величины X, X, X кумулятивная функция распределения FXF_XFX определяется как FX(x)=P(X≤x),F_X(x) = P(X \leq x),FX(x)=P(X≤x), , то есть вероятность того, что XXX меньше или равно x.x.x. 9b f_X (x) \,dx.P(a≤X≤b)=∫abfX(x)dx. Теперь вероятность переписывается как разность значений CDF: P(a≤X≤b)=FX(b)−FX(a).P(a \leq X \leq b) = F_X (б) — F_X(a).P(a≤X≤b)=FX(b)−FX(a). Таким образом, CDF дает площадь под PDF между двумя точками. Он увеличивается от нуля (для очень низких значений xxx) до единицы (для очень высоких значений xxx). Это связано с тем, что при x→−∞x \to -\inftyx→−∞ вероятность того, что XXX будет найдена так далеко, отсутствует, если PDF нормализован. Если x→∞x \to \inftyx→∞, это соответствует P(X≤∞)P(X \leq \infty)P(X≤∞), что будет единицей, поскольку несомненно, что XXX принимает некоторое конечное значение. В случае дискретных случайных переменных значение FXF_XFX совершает дискретный скачок при всех возможных значениях xxx; размер скачка соответствует вероятности P(X=x)P(X=x)P(X=x) этого значения. P(X∈[a,b])=P(a≤X≤b)=FX(b)−FX(a).P(X \in [a,b]) = P( a ≤ X ≤ b) = F_X(b)-F_X(a).P(X∈[a,b])=P(a≤X≤b)=FX(b)−FX(a). Обратите внимание, что не имеет значения, являются ли неравенства строгими (если интервал равен [a,b][a,b][a,b] или (a,b)(a,b)(a,b) для пример): поскольку вероятность любого заданного значения равна нулю, конечные точки могут быть включены или нет без изменения каких-либо вероятностей. Тем не менее, часто требуется использовать функцию плотности вероятности fX(x)f_X (x)fX(x), а не CDF. Поскольку CDF соответствует интегралу PDF, PDF соответствует производной CDF: fX(x)=FX'(x)=dFXdx.f_X(x) = F_X'(x) = \frac{dF_X}{dx} .fX(x)=FX’(x)=dxdFX . Решение: Это распределение вероятностей является однородным , что означает, что плотность вероятности постоянна на всем интервале [0,30][0, 30][0,30]. Это означает, что FXF_XFX является линейной функцией:
FX(x)={0x≤0x300≤x≤30130≤x.F_X(x) = \left\{\begin{array}{ll} 0 & x \leq 0 \\ \frac{x}{30} & 0 \leq x \leq 30 \\ 1 & 30 \leq x. \end{массив}\right.FX(x)=⎩⎨⎧030x1x≤00≤x≤3030≤x.
Функция плотности вероятности является производной:
fX(x)={0x≤01300≤x≤30030≤x.f_X(x) = \left\{\begin{array}{ll} 0 & x \leq 0 \\ \frac{1}{30} & 0 \leq x \leq 30 \\ 0 & 30 \leq x. \end{массив}\right.fX(x)=⎩⎨⎧03010x≤00≤x≤3030≤x. Следовательно, функция плотности вероятности при x=5x = 5x=5 равна 130.\frac{1}{30}.301. 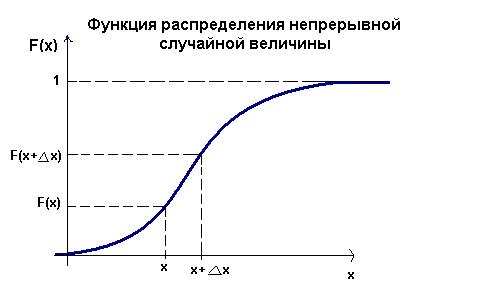
Повторный просмотр примера 14-2
Раздел
Решение
\end{массив}\right.\end{уравнение}\) непрерывных случайных величин — кумулятивная функция распределения
Содержимое
 В случае непрерывной случайной величины функция непрерывно возрастает; не имеет смысла говорить о вероятности того, что X=xX = xX=x, потому что эта вероятность всегда равна нулю. Вместо этого рассматривается вероятность того, что значение XXX лежит в данных интервал :
В случае непрерывной случайной величины функция непрерывно возрастает; не имеет смысла говорить о вероятности того, что X=xX = xX=x, потому что эта вероятность всегда равна нулю. Вместо этого рассматривается вероятность того, что значение XXX лежит в данных интервал : Муха приземляется на линейку длиной 30 см30\text{ cm}30 см в случайном месте, равномерно выбранном вдоль линейки.
 Пусть XXX будет положением мухи в сантиметрах, и пусть fX(x)f_X(x)fX(x) будет функцией плотности вероятности для X.X.X. Что такое fX(5)f_X(5)fX(5)?
Пусть XXX будет положением мухи в сантиметрах, и пусть fX(x)f_X(x)fX(x) будет функцией плотности вероятности для X.X.X. Что такое fX(5)f_X(5)fX(5)? Игрок в дартс всегда попадает в мишень для дротиков (с радиусом 20 см20\text{ см}20 см), но прицеливается настолько плохо, что дротики распределяются равномерно по всей доске.

