Нормальный закон распределения — презентация онлайн
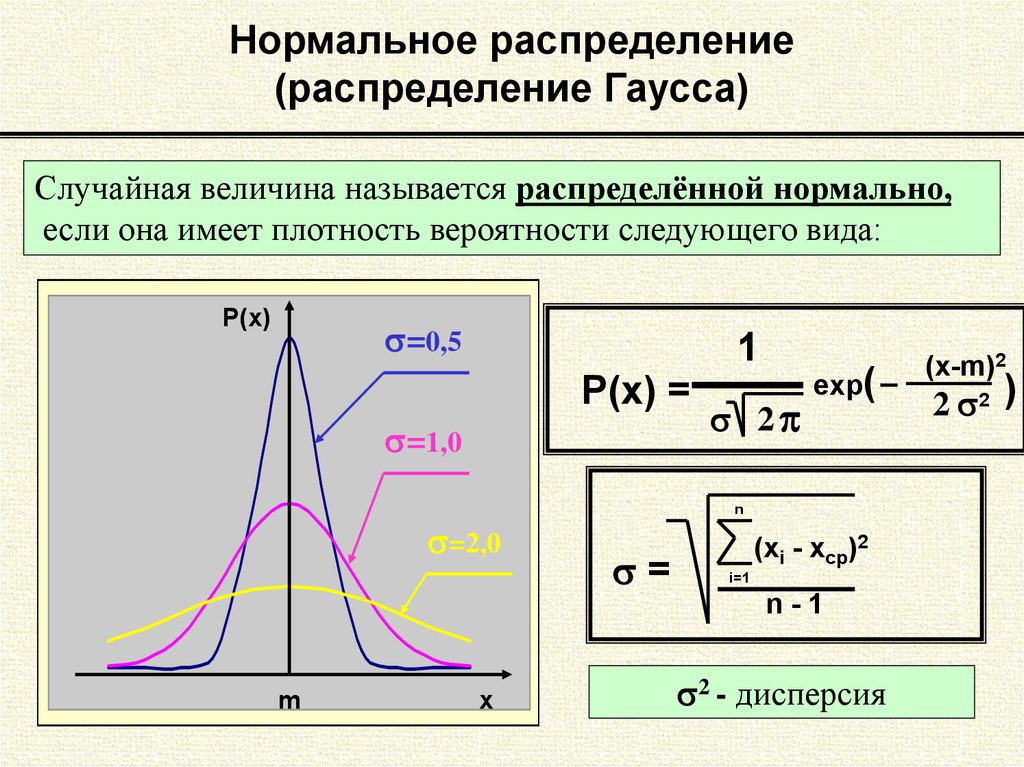
Нормальный закон распределения
Функция распределения F(x) и соответствующая ей плотность распределения f(x)
представляют собой некоторую математическую модель свойств исследуемой
случайной величины (отклика), значения которой регистрируются в
ходе эксперимента.
Поэтому одной из основных задач статистической обработки опытных данных
является нахождение таких функций распределения, которые, с одной стороны,
достаточно хорошо описывали бы наблюдаемые значения случайной величины, а
с другой – были бы удобны для дальнейшего статистического анализа.
При этом вид функции распределения предпочтительно выбирать на основе
представлений о физической природе рассматриваемого явления, т.к. в этом
случае исключаются возможные погрешности при распространении найденных
закономерностей за пределы изучаемого в эксперименте интервала варьирования
(изменения) случайной величины (отклика).
Из всех изученных к настоящему времени случайных величин при обработке
экспериментальных данных исследователи чаще всего оперируют со
случайными величинами, которые имеют так называемое нормальное (Гауссово)
распределение (рис. 3).
3).
Не вдаваясь в подробные математические выкладки, отметим, что, согласно
центральной предельной теореме математической статистики,
«при определенных условиях распределение нормированной суммы n
независимых случайных величин, распределенных по произвольному закону,
стремится к нормальному, когда n стремится к бесконечности».
Необходимые условия, при которых эта теорема оказывается справедливой,
состоят в том, что различные случайные величины должны иметь конечные
дисперсии и дисперсия любой случайной величины не должна быть слишком
большой по сравнению с дисперсиями других.
При обработке экспериментальных данных эта теорема имеет очень
большое значение, поскольку отклик становится случайной величиной в
результате влияния неконтролируемых факторов, число которых скорее
всего стремится к бесконечности.
Кроме того, если при проведении опытов все наиболее существенные факторы
контролируются, то воздействие на отклик каждого из неконтролируемых
факторов не должно быть слишком большим по сравнению с
остальными неконтролируемыми факторами.
Другими словами, та дисперсия (рассеивание) отклика, которую вызывает какойлибо из неконтролируемых факторов, не должна сильно отличаться от дисперсий,
связанных с влиянием остальных неконтролируемых факторов. В противном
случае фактор, дисперсия от которого существенно отличается от других,
обязательно должен быть переведен в разряд контролируемых.
Следовательно, если при планировании эксперимента учтены все наиболее
существенные факторы и затем, при проведении опытов, они контролируются, то
при обработке экспериментальных данных можно предполагать, что
отклик не должен противоречить нормальному распределению.
При обработке результатов наблюдений исследователи прежде всего
предполагают именно нормальное распределение отклика.
Большинство других распределений, которые используются в математической
статистике (Стьюдента, Фишера, Пирсона, Кохрена, а также распределения, по
которым составлены различные критериальные таблицы), получены на основе
нормального распределения.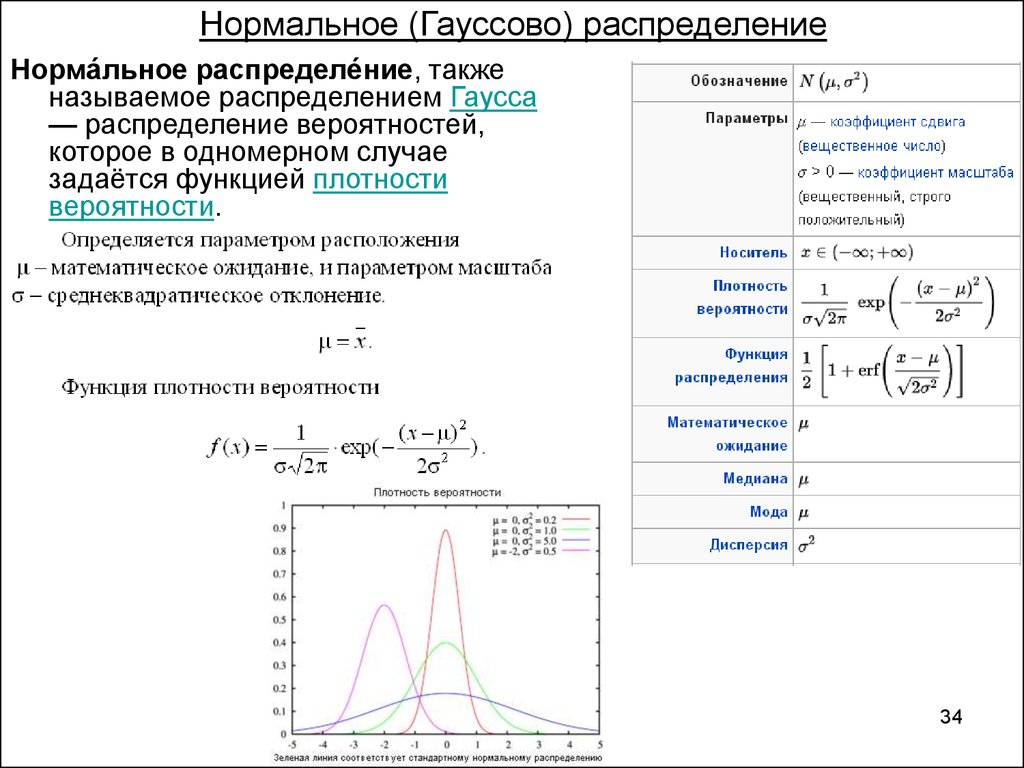
Нельзя, однако, абсолютизировать значение нормального распределения.
Не все случайные величины распределены по нормальному закону. Тем не
менее на практике, если явление подвержено действию многих случайных
факторов, их суммарное воздействие вполне оправданно можно описать с
помощью нормального закона.
Как уже было отмечено, для случайной величины, которая не противоречит
нормальному закону, функция распределения (12) и соответствующая ей
плотность распределения
F ( x)
1
2 x2
x
e
( x M x )2
2 x2
dx,
(21)
определяются двумя параметрами: Мx – математическим ожиданием и σx2 –
дисперсией.
Отметим некоторые свойства нормального закона распределения.
1. Кривая плотности распределения симметрична относительно значения
Мx, называемого иногда центром распределения.
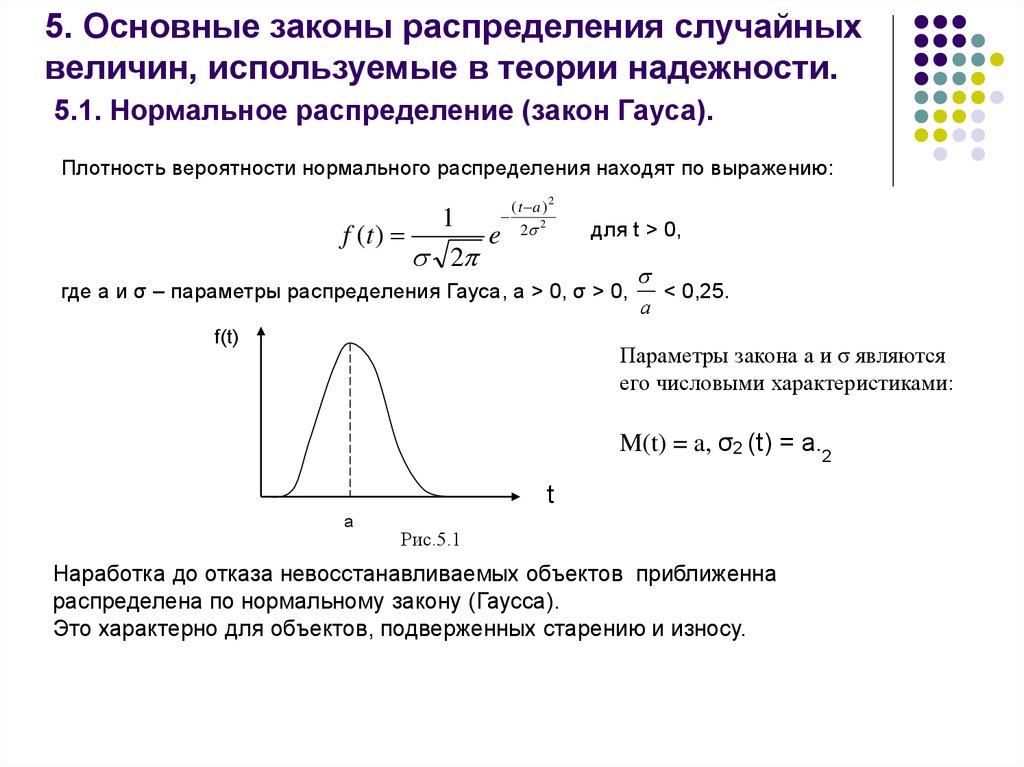
2. При больших значениях σx2 кривая f(x) более пологая, т.е. σx2 является
мерой величины рассеивания значения случайной величины около значений
Мx.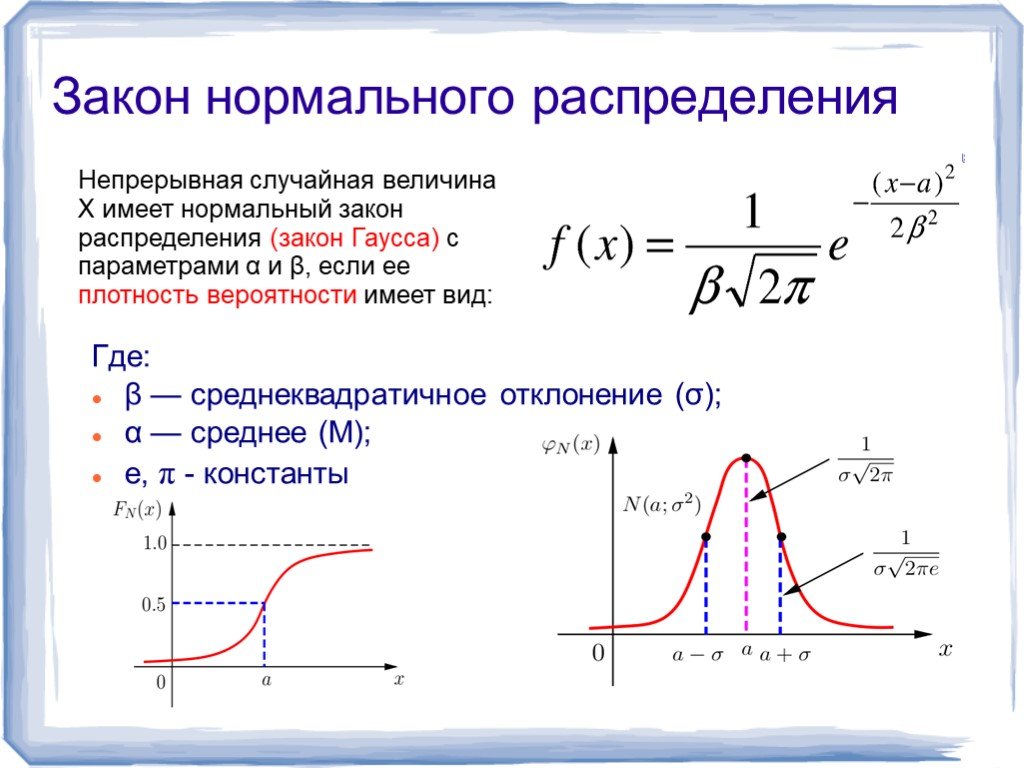 При уменьшении параметра σx2 кривая нормального распределения
При уменьшении параметра σx2 кривая нормального распределения
сжимается вдоль оси ОХ и вытягивается вдоль f(x).
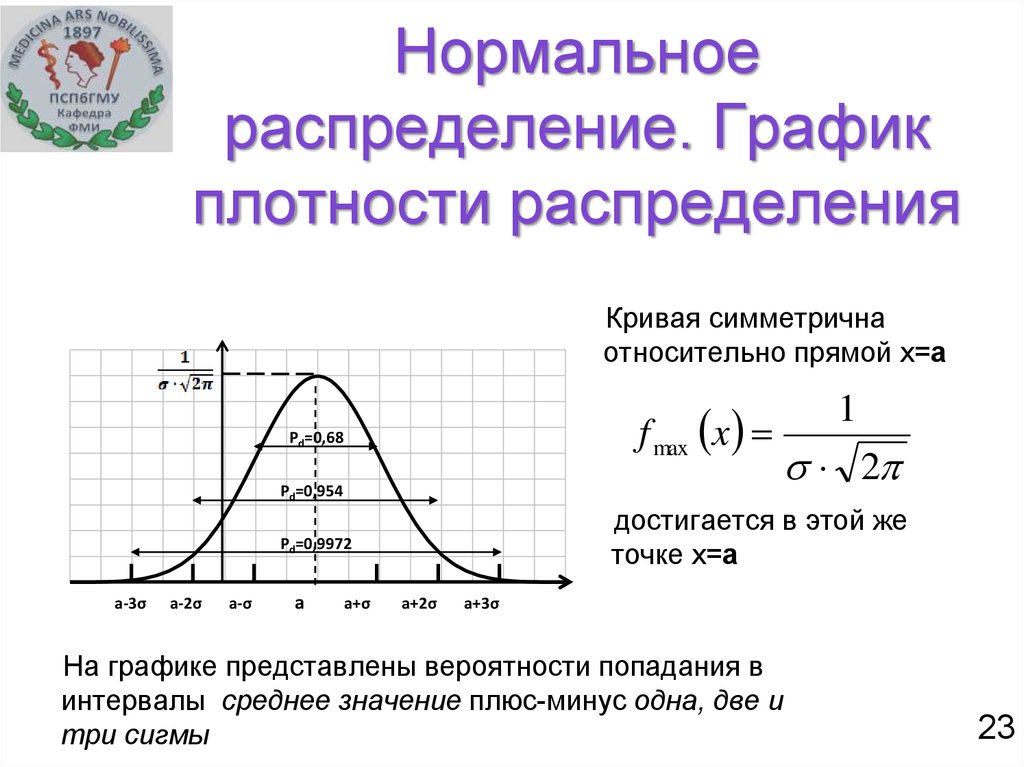
3. Максимум ординаты кривой плотности распределения определяется
выражением
f max
1
2
2
x
,
что при σx2 =1 соответствует значению примерно 0,4.
4. Для нормального распределения математическое ожидание, мода и
медиана совпадают:
M x M 0 M e.
(23)
В ряде случаев рассматривается не сама случайная величина Х, а ее
отклонение от математического ожидания:
Y X M.
(24)
Такая случайная величина Y называется центрированной.
Отношение случайной величины Х к ее среднему квадратичному отклонению
V
X
x
называется нормированной случайной величиной.
(25)
Таким образом, центрированная случайная величина – разность между
данной случайной величиной и ее математическим ожиданием, а нормированная
случайная величина – отношение данной случайной величины к ее среднему
квадратичному отклонению.
Очевидно, что математическое ожидание центрированной случайной величины
равно нулю, My = 0, а дисперсия нормированной случайной величины равна
единице, σV 2 = 1.
Приведенная случайная величина – центрированная и нормированная
случайная величина
Z
X Mx
x
(26)
Математическое ожидание и дисперсия приведенной случайной величины Z равны
соответственно нулю, Mz= 0, и единице, σz 2 = 1.
Нормальное распределение с параметрами Mz= 0 и σz 2 = 1 называется
стандартным (нормированным)
Для приведенной случайной величины нормальное стандартное распределение принимает вид
1 z
F ( z)
e
2
1
f ( z)
2
z2
2
dz Ф( z ),
z2
e 2
( z ).
(27)
(28)
Графики этих функций показаны на рис. 3 в, г, причем
Ф( –z) = 1 – Ф(z),
φ(-z)= φ(z ).
(29)
(30)
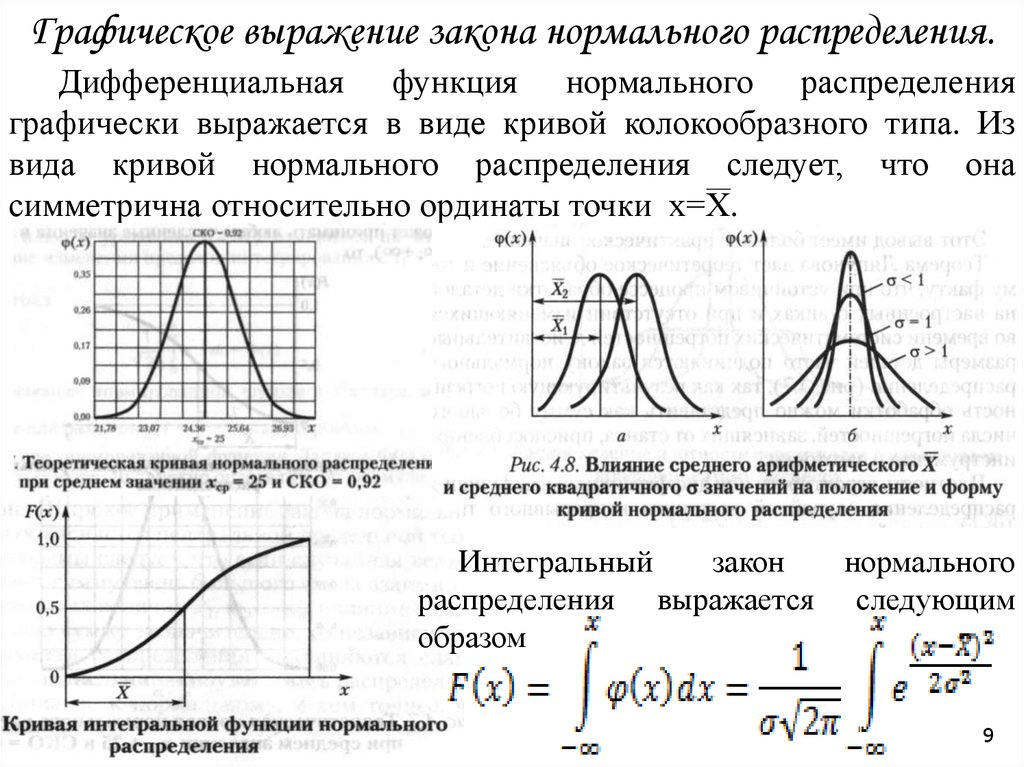
Рис.3. Плотность распределения (а,г) и функция
распределения (б,в) при нормальном законе распределения
случайных величин
Значения нормированной функции (27) нормального распределения
(функции Лапласа) и значения плотности нормированного нормального
распределения (28) табулированы и приведены в различных учебниках и
справочниках по математической статистике
В списке статистических функций электронных таблиц Microsoft Excel им соответствуют НОРМРАСП(x; 0; 1; ИСТИНА) или НОРМСТРАСП(z) – для (27) и
НОРМРАСП(x; 0; 1; ЛОЖЬ) – для (28).
Геометрически функция Лапласа представляет площадь под кривой f(z) в
интервале от −∞ до некоторой конкретной величины z.
Заметим, что иногда вместо функции Ф(z) табулируется функция Ф0(z):
z
1
Ф0 ( z )
e
2 0
z2
2
dz,
равная площади под графиком стандартного нормального распределения от 0
до z (см. рис. 3, г).
2
z
В силу симметрии
0
2
1
e
2
dz 1 / 2.
Поэтому между функциями и существует простая зависимость
Ф(z)= Ѕ+ Ф0(z).
Функция Ф0(z) нечетна:
Ф0(-z) = — Ф0(z).
В самом деле,
Ф0(-z) = Ф(-z) – Ѕ = 1 — Ф(z) – Ѕ = Ѕ-(1/2+ Ф0(-z)) = — Ф0(z).
В соответствии с (19) квантиль zр порядка р, нормированного нормального закона
распределения — это такое значение приведенной случайной величины Z, для
которого функция распределения (27) принимает значение Р:
Ф(zp) = P.
(31)
При определении квантили zр необходимо решать задачу, обратную задаче
определения значений функции Лапласа, т.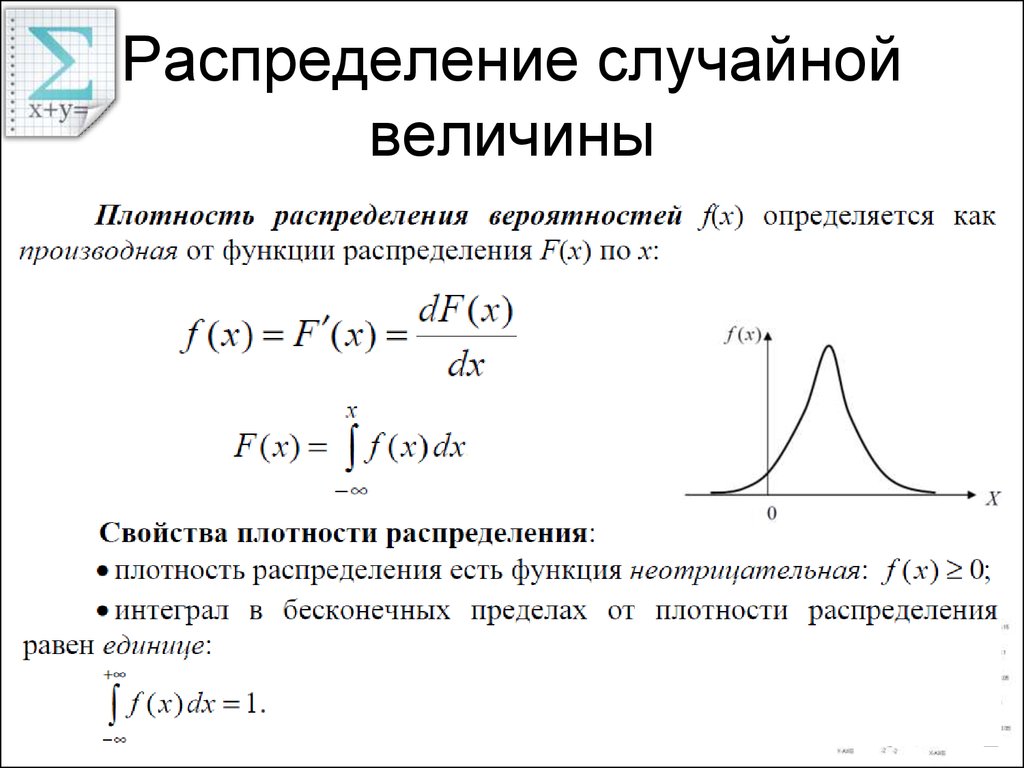 е. по известному значению Р
е. по известному значению Р
этой функции (27) находить соответствующее ему значение аргумента zр.
Для этого можно либо воспользоваться табулированными значениями функции
Лапласа (например, поскольку Ф(1,64) = 0,94950, а Ф(1,65) = 0,9505, то z0,95 ≈
1,645 ), либо воспользоваться таблицами для функции, обратной функции
Лапласа, т.е. табулированными значениями квантилей нормированного
нормального закона распределения.
Определение квантили zp в электронных таблицах Microsoft Excel сводится к
вычислению статистической функции НОРМОБР(Р; 0; 1) или НОРМСТОБР(Р)
(например, НОРМОБР(0,95; 0; 1) = НОРМСТОБР(0,95) = 1,644853).
Для квантили стандартного нормального распределения справедливо
следующее равенство:
z1 – p = — zp.
(27)
Рассмотрим график плотности стандартного нормального распределения
(рис.4). Площадь под графиком левее квантили zp по определению равна p.
Значит, площадь правее этой точки равна 1 – p. Такая же площадь расположена
левее точки z1 –p Итак, площади левее z1 –p и правее zp равны.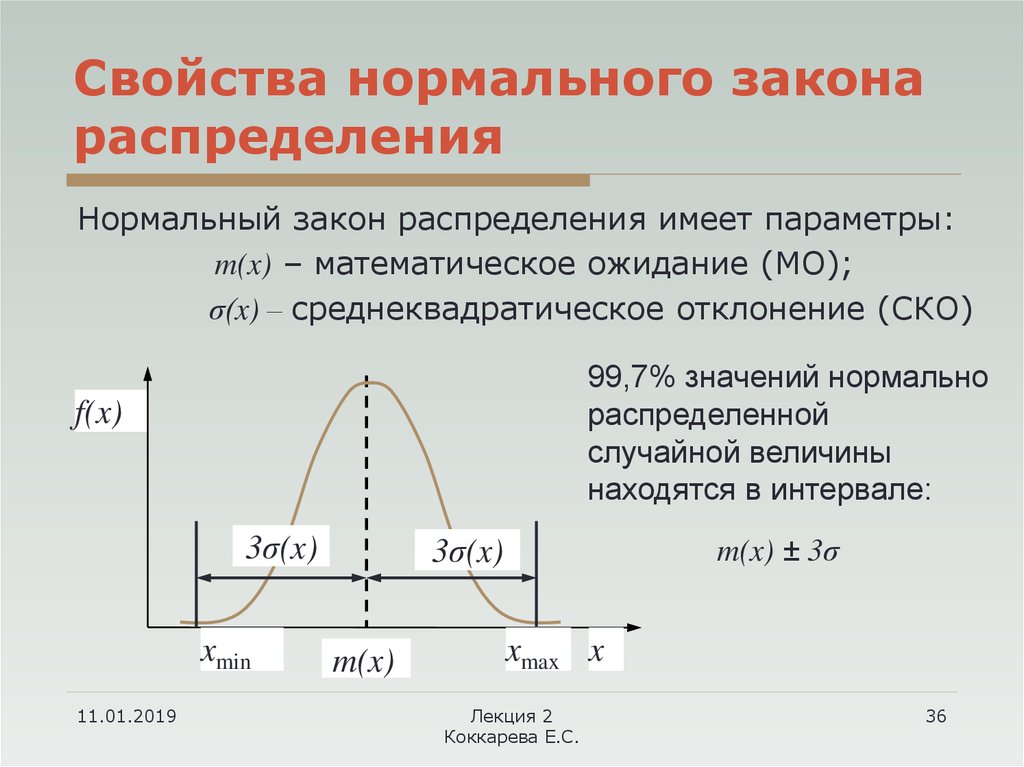 Поскольку
Поскольку
график симметричен относительно оси ординат, из этого следует, что эти точки
расположены на одинаковом расстоянии от нуля.
Рис.4. Квантиль стандартного
нормального распределения
Зная квантиль zр порядка р нормированного нормального закона распределения
(Mz = 0 и σz 2 = 1), всегда можно найти квантиль xр соответствующего
2
порядка р для нормального распределения с произвольными параметрами σz
Поскольку
то
X M x xp M x
F ( x p ) P ( X x p ) P
x
x
xp M x
xp M x
Ф
Р Ф( z p ),
P Z
x
x
xp M x
x
и, следовательно,
zp
x p M x z p x .
(32a)
В ряде случаев важно знать вероятность того, что случайная величина Х,
подчиняющаяся нормальному закону распределения, не будет отличаться от
своего математического ожидания Мx больше чем на величину ±δ = ε·σx
(см.рис.3,г).
M x M x X M x M x x M x
P( M x X M x ) P x
x
x
x
z2
2
1
1
P Z
e dz
e
2
2
Ф( ) (1 Ф( )) 2Ф( ) 1.
z2
2
dz Ф( ) Ф( ),
Так, при δ = σx (ε =1) получаем, что P(Mx + σx < X ≤ Mx −σx ) = 2Φ(1)−1, а
поскольку по таблицам Ф(1) = 0,84135 (или в Microsoft Excel
НОРМРАСП(1;0;1;ИСТИНА) = НОРМСТРАСП(1) = 0,84135), то для случайной
величины с нормальным законом распределения вероятность того, что
она примет такое значение, которое не будет отличаться от ее математического
ожидания более чем на одно среднее квадратическое отклонение, равна
2⋅0,84135–1=0,68. Иными словами, при нормальном распределении примерно
2/3 всех значений случайной величины (отклика) лежит в интервале Mx ± σx.
Аналогично можно подсчитать, что интервалу Mx ± 1,96σx ≈ Mx ± 2σx соответствует
вероятность 0,95 (Ф(1,96) = 0,975002), а интервалу Mx ± 3σx — 0,997
(Ф(3) = 0,99865)
.
Отметим дополнительно, что 90% значений случайной величины лежат в
диапазоне Mx ± 1,64σx (Ф(1,64) = 0,949497).
Следовательно, отличие какого-либо из значений случайной величины
с нормальным законом распределения от ее математического ожидания не
превосходит утроенного среднего квадратичного отклонения с вероятностью 0,997.
Это свойство в математической статистике носит название «правило трех
сигм».
Чем больше величина интервала Mx ± δ, тем с большей вероятностью
случайная величина X попадает в этот интервал.
Рассмотрим небольшой пример.
Пример 2. Предположим, что математическое ожидание содержания
cеры в угле равно MS=0,6%, а среднеквадратичное отклонение σS=0,15%.
В этом случае мы можем быть уверены в том, что величина фактически
измеренного значения процентного содержания cеры в угле будет находиться
в интервалах:
0,6 ± 1,00⋅0,15 = 0,6±0,15 с вероятностью 0,68;
0,6 ± 1,64⋅0,15 = 0,6±0,25 с вероятностью 0,90;
0,6 ± 1,96⋅0,15 = 0,6±0,29 с вероятностью 0,95;
0,6 ± 3,00⋅0,15 = 0,6±0,45 с вероятностью 0,997,
т.е. из 1000 проб только 3 пробы по содержанию cеры в угле будут выходить из
диапазона от 0,15 до 1,05%.
Заметим, однако: при рассмотрении примера 2 мы предполагали, что процентное
содержание cеры в угле не противоречит нормальному закону распределения, а
также то, что нам изначально были известны математическое ожидание Mx и
среднеквадратичное отклонение σx этой случайной величины, т. е. было
е. было
выполнено большое (в пределе бесконечное) число измерений.
Как же работать со случайными величинами в реальных условиях проведения
эксперимента, когда число измерений весьма ограничено?
К рассмотрению методологии решения подобных задач мы и перейдем в
следующих лекциях.
на предыдущую на следующую Законы распределения непрерывных случайных величин Закон распределения непрерывной случайной величины
нельзя задать также, как для дискретной. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: . Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с
помощью функции распределения не является единственным. Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения: . Про случайную величину Х говорят, что она имеет распределение (распределена) с плотностью f(x) на определенном участке оси абсцисс. Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной
плотности) на отрезке [a; b], если на
этом отрезке функция плотности вероятности случайной величины постоянна, т.
Математическое ожидание Дисперсия: Величина называется поправкой Шеппарда.
Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]:
Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника.
Пример 4. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.
Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами и (обозначают ), если ее плотность вероятности имеет вид:
Математическое ожидание характеризует центр рассеивания значений случайной величины и при изменении кривая будет смещаться вдоль оси абсцисс (см. рис. 2 при и при ). Если же при неизменном математическом ожидании у случайной величины изменяется дисперсия, то кривая будет изменять свою форму, сжимаясь или растягиваясь (см. рис. 2 при : ; ; ). Таким образом, параметр характеризует положение, а параметр — форму кривой плотности вероятности. Нормальный закон распределения случайной величины Х с параметрами и (обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной. Согласно определению функция плотности вероятности и функция распределения связаны между собой: , где . Интеграл такого рода является «неберущимся», поэтому для его нахождения используют
особую функцию, так называемый интеграл
вероятностей или функцию Лапласа,
для которой составлены таблицы (см.
Используя функцию Лапласа можно выразить функцию распределения нормального закона по формуле: , где . Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения. 1. Если , то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула: . 2. Вероятность того, что отклонение случайной величины от ее математического ожидания не превысит величину (по абсолютной величине), равна: . 3. «Правило
трех сигм». Если случайная
величина , то практически достоверно, что ее значения заключены
в интервале (). Пример 5. Случайная величина распределена нормально с параметрами , . Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14). . Пример 6. Случайная погрешность измерения подчинена нормальному закону распределения с параметрами , . Проводятся три независимых измерения. Найти вероятность того, что погрешность хотя бы одного измерения не превосходит по абсолютной величине 3 мм. Вероятность того, что погрешность измерения в одном испытании не превышает 3 мм: . Вероятность того, что эта погрешность измерения в одном испытании превышает 3 мм, равна: . Вероятность того, что во всех трех испытаниях погрешность измерения превышает 3 мм: . Искомая вероятность: . Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез. Синтаксис НОРМРАСП(x;среднее;стандартное_откл;интегральная) x — значение, для которого строится распределение. Среднее — среднее арифметическое распределения. Стандартное_откл — стандартное отклонение распределения. Интегральная — логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения. Замечания · Если аргумент «среднее» или «стандартное_откл» не является числом, функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!. · Если стандартное_откл ≤ 0, то
функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!. · Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП. · Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид: · Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x. Возвращает стандартное нормальное интегральное распределение. Это распределение имеет среднее, равное нулю, и стандартное отклонение, равное единице. Данная функция используется вместо таблицы площадей стандартной нормальной кривой. Синтаксис НОРМСТРАСП(z) Z — значение, для которого строится распределение. Замечания · Если z не является числом, функция НОРМСТРАСП возвращает значение ошибки #ЗНАЧ!. · Уравнение плотности стандартного нормального распределения имеет следующий вид: Возвращает обратное нормальное распределение для указанного
среднего и стандартного отклонения. Синтаксис НОРМОБР(вероятность;среднее;стандартное_откл) Вероятность — вероятность, соответствующая нормальному распределению. Среднее — среднее арифметическое распределения. Стандартное_откл — стандартное отклонение распределения. Замечания · Если какой-либо из аргументов не является числом, функция НОРМОБР возвращает значение ошибки #ЗНАЧ!. · Если вероятность < 0 или вероятность > 1, функция НОРМОБР возвращает значение ошибки #ЧИСЛО!. · Если стандартное_откл ≤ 0, функция НОРМОБР возвращает значение ошибки #ЧИСЛО!. · Если среднее = 0 и стандартное_откл = 1, функция НОРМОБР использует стандартное нормальное распределение (см. НОРМСТОБР). Если задано значение вероятности, функция НОРМОБР ищет значение x, для которого функция НОРМРАСП(x,
среднее, стандартное_откл, ИСТИНА) = вероятность.
Однако точность функции НОРМОБР зависит от точности НОРМРАСП.
в начало на предыдущую на следующую | ||||||||||||||||||||||||||
scipy.stats.norm — Руководство по SciPy v1.10.0
- scipy.stats.norm = <объект scipy.stats._continuous_distns.norm_gen> [источник]
Нормальная непрерывная случайная величина.
Ключевое слово location (
loc) определяет среднее значение. Ключевое слово масштаба (scale) определяет стандартное отклонение.Как экземпляр класса
rv_continuous, объектnormнаследуется от него набор универсальных методов (полный список см. ниже), и дополняет их деталями, характерными для данного конкретного дистрибутива. 92/2)}{\sqrt{2\pi}}\]для действительного числа \(x\).

Приведенная выше плотность вероятности определена в «стандартизированной» форме. Переключать и/или масштабировать распределение, используя параметры
locиscale. В частности,norm.pdf(x, loc, scale)тождественно эквивалентнонорм.pdf(y)/шкаласy = (x - loc) / шкала. Обратите внимание, что смещение местоположения дистрибутива не делает его «нецентральным» распределением; нецентральные обобщения некоторые дистрибутивы доступны в отдельных классах.Примеры
>>> импортировать numpy как np >>> из scipy.stats норма импорта >>> импортировать matplotlib.pyplot как plt >>> рис, топор = plt.subplots(1, 1)
Рассчитать первые четыре момента:
>>> среднее, вар, перекос, курт = norm.stats(moments='mvsk')
Показать функцию плотности вероятности (
pdf):>>> x = np.linspace(norm.ppf(0.01), ... норма.ppf(0,99), 100) >>> ax.plot(x, norm.
 pdf(x),
... 'r-', lw=5, альфа=0,6, метка='норма pdf')
pdf(x),
... 'r-', lw=5, альфа=0,6, метка='норма pdf')
В качестве альтернативы можно вызвать объект распределения (как функцию) зафиксировать параметры формы, местоположения и масштаба. Это возвращает «замороженный» Объект RV с фиксированными заданными параметрами.
Заморозить дистрибутив и отобразить замороженный
pdf:>>> rv = норма() >>> ax.plot(x, rv.pdf(x), 'k-', lw=2, label='замороженный pdf')
Проверка точности
cdfиppf:>>> vals = norm.ppf([0,001, 0,5, 0,999]) >>> np.allclose([0,001, 0,5, 0,999], norm.cdf(vals)) Истинный
Генерация случайных чисел:
>>> r = норма.rvs(размер=1000)
И сравните гистограмму:
>>> ax.hist(r,density=True, bins='auto', histtype='stepfilled', alpha=0.2) >>> ax.set_xlim([x[0],x[-1]]) >>> ax.legend(loc='лучший', frameon=False) >>> plt.show()
Методы
rvs(loc=0, scale=1, size=1, random_state=None)
Случайные величины.

pdf(x, loc=0, масштаб=1)
Функция плотности вероятности.
logpdf(x, loc=0, масштаб=1)
Логарифм функции плотности вероятности.
cdf(x, loc=0, масштаб=1)
Суммарная функция распределения.
logcdf(x, loc=0, масштаб=1)
Лог интегральной функции распределения.
sf(x, loc=0, масштаб=1)
Функция выживания (также определяется как
1 - cdf, но sf иногда является более точным).logsf(x, loc=0, масштаб=1)
Журнал функции выживания.
ppf(q, loc=0, масштаб=1)
Функция процентной точки (обратная
cdf— процентили).
isf(q, loc=0, scale=1)
Обратная функция выживания (обратная
sf).момент (порядок, loc=0, масштаб=1)
Нецентральный момент указанного порядка.
статистика(лок=0, масштаб=1, моменты=’mv’)
Среднее (‘m’), дисперсия (‘v’), перекос (‘s’) и/или эксцесс (‘k’).
энтропия (loc=0, scale=1)
(Дифференциальная) энтропия ВС.
подходит(данные)
Оценки параметров для общих данных. Подробную документацию по аргументам ключевого слова см. в scipy.stats.rv_continuous.fit.
ожидаемое (функция, args=(), loc=0, масштаб=1, lb=нет, ub=нет, условное=ложь, **kwds)
Ожидаемое значение функции (одного аргумента) относительно распределения.

медиана (loc=0, scale=1)
Медиана распределения.
среднее (loc=0, scale=1)
Среднее значение распределения.
var(loc=0, scale=1)
Дисперсия распределения.
станд.(лок.=0, масштаб=1)
Стандартное отклонение распределения.
интервал (достоверность, loc=0, масштаб=1)
Доверительный интервал с равными площадями вокруг медианы.
Формула нормального распределения — Что такое формула нормального распределения?
Нормальное распределение, или кривая нормального распределения, или гауссово распределение является наиболее значимым непрерывным распределением вероятностей в вероятности и статистике.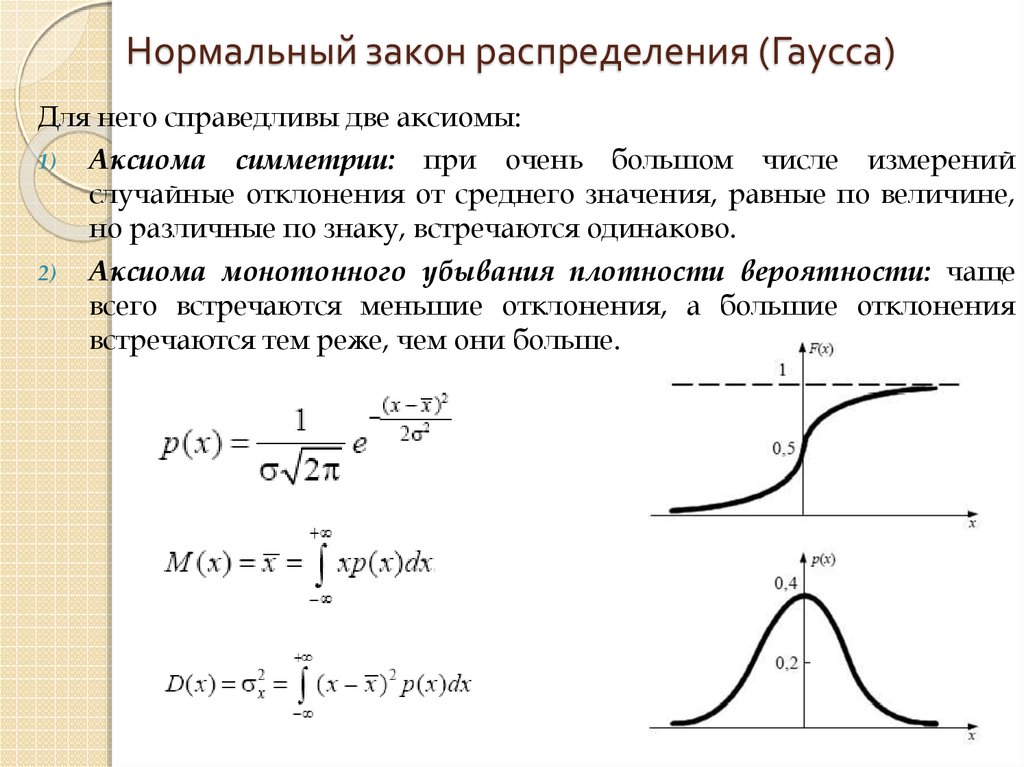 В физике и экономике огромное количество представляющих интерес случайных величин почти или точно описываются нормальным распределением. Формула нормального распределения также может быть использована для аппроксимации других вероятностных распределений.
В физике и экономике огромное количество представляющих интерес случайных величин почти или точно описываются нормальным распределением. Формула нормального распределения также может быть использована для аппроксимации других вероятностных распределений.
Случайные величины, которые следуют нормальному распределению, — это те, значения которых могут принимать любое известное значение в заданном диапазоне.
Что такое формула нормального распределения?
Нормальное распределение определяется функцией плотности вероятности f(x) для непрерывной случайной величины X, рассматриваемой в системе. Это функция, интеграл которой по интервалу (скажем, от x до x + dx) дает вероятность случайной величины X при рассмотрении значений между x и x + dx. Поскольку между x и x + dx будут бесконечные значения, таким образом, рассматривается диапазон x, а непрерывная функция плотности вероятности определяется как 9{2}}}\)
Где,
\(\mathrm{x}\) – это переменная
.
\(\mu\) – это среднее 90 337
\(\sigma\) – стандартное отклонение
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами. формула распределения. 92 }) \)
Узнайте, почему математика стоит за нашими сертифицированными экспертами. формула распределения. 92 }) \)
Чтобы использовать формулу нормального распределения, пусть \(Z = \frac{{X — \mu}}{\sigma}=\frac{{X — 4}}}{3}\)
Следовательно,
\(P\left({X > 6} \right) = 1 — P\left( {X < 6} \right) \\ = 1 - \varphi \left( {\frac{{6 - 4}}{ 3}} \right) \\ = 1 - \varphi \left( {0,67} \right) \\ = 1 - 0,74857 \\ = 0,25143\)
Ответ: \( P(X>6)=0,25143 \)
Пример 2: Срок службы электрической лампочки определенной марки распределен со средним значением 1200 часов и стандартным отклонением 200 часов. Какова вероятность того, что лампочка проработает более 1150 часов? Используйте формулу нормального распределения. 92 }) \)
Отсюда
\( P\left( {X > 1150} \right) = 1 — P\left( {X < 1150} \right) \\ = 1 - \varphi \left( {\frac{1150 - 1200}{200} } \right) \\ = 1 - \varphi \left( {-0,25} \right) \\ = 0,59871\)
Ответ: Вероятность того, что лампочка проработает более 1150 часов, равна 0,59871.
Пример 3. Какой будет функция плотности вероятности нормального распределения данных; \(x=3, \mu=\) 4 и \(\sigma=2\)?
Решение: 9009{2}}}\)
Где,
\(\mathrm{x}\) – это переменная
.
\(\mu\) – это среднее 90 337
\(\sigma\) – стандартное отклонение
Каковы характеристики нормального распределения?
Важными характеристиками нормального распределения являются:
- Симметричность и унимодальность
- Среднее значение, медиана и мода равны.
- Нормальное распределение очень симметрично относительно своего центра. Левая сторона центра пика является зеркальным отражением правой стороны.
Что такое стандартное нормальное распределение?
Стандартное нормальное распределение — это нормальное распределение со средним значением, равным нулю, и стандартным отклонением, равным 1. Для каждого стандартного нормального распределения 68% наблюдений лежат в пределах 1 стандартного отклонения от среднего; 95% лежат в пределах двух стандартных отклонений от среднего, а 99,9% лежат в пределах 3 стандартных отклонений от среднего.

 Он неприменим в силу того, что нельзя
перечислить все бесконечное несчетное множество значений, а вероятности каждого
отдельно взятого значения непрерывной случайной величины равны нулю.
Он неприменим в силу того, что нельзя
перечислить все бесконечное несчетное множество значений, а вероятности каждого
отдельно взятого значения непрерывной случайной величины равны нулю.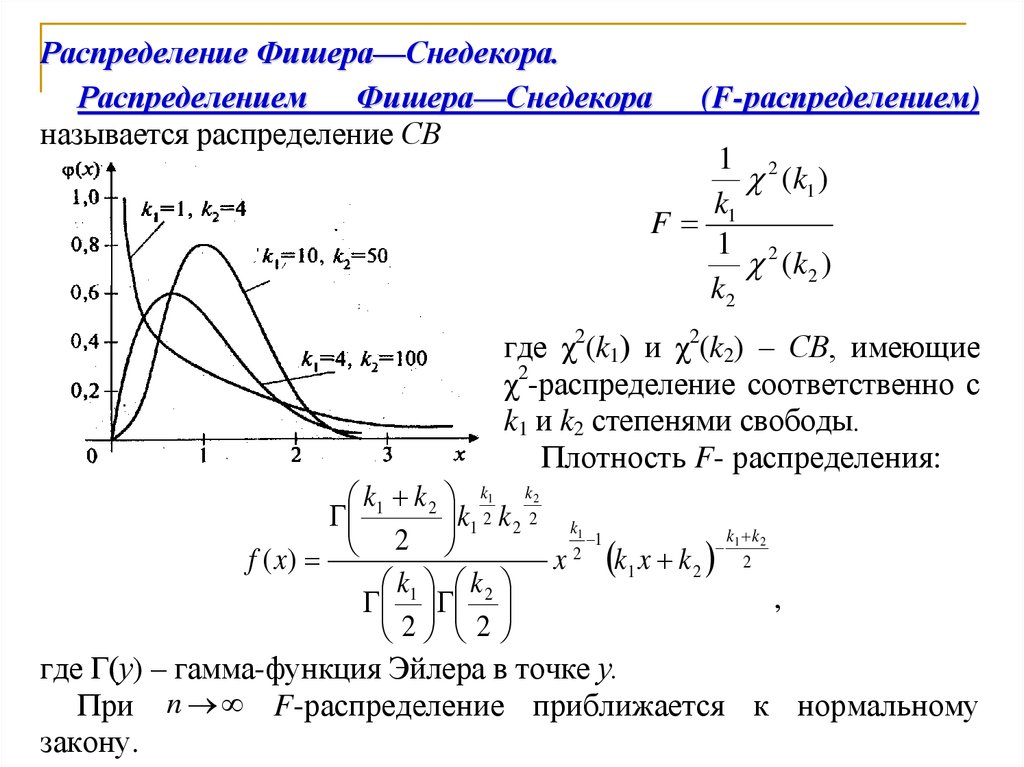
 е. f(x) имеет вид:
е. f(x) имеет вид: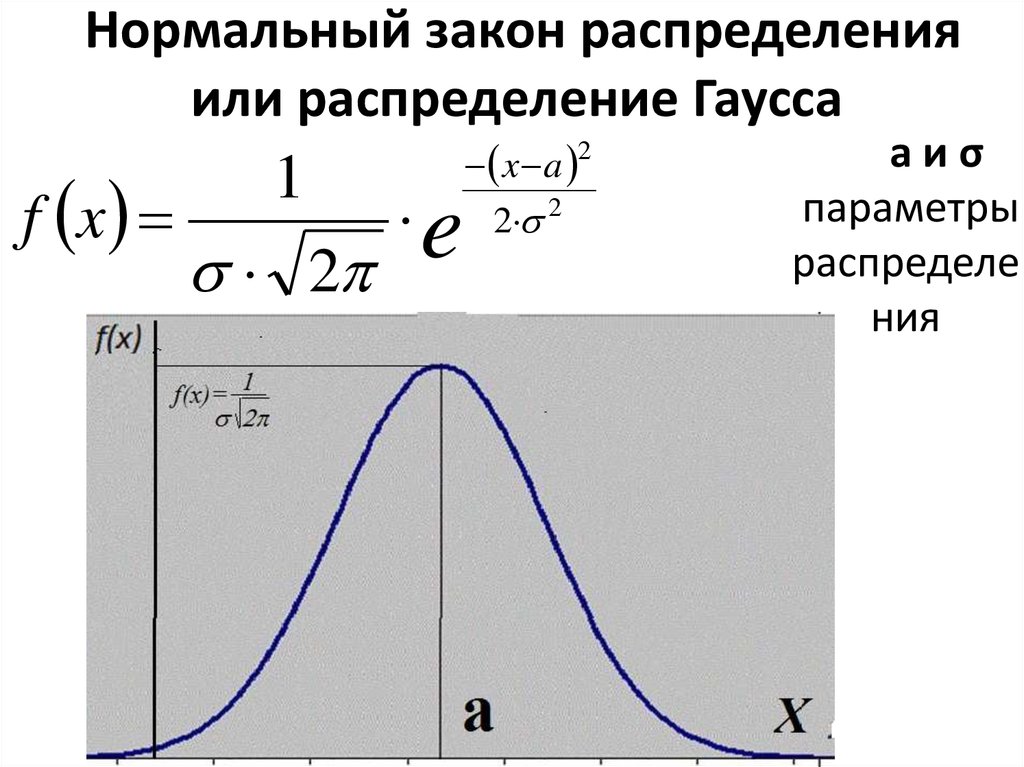
 2. Нормальный закон распределения
2. Нормальный закон распределения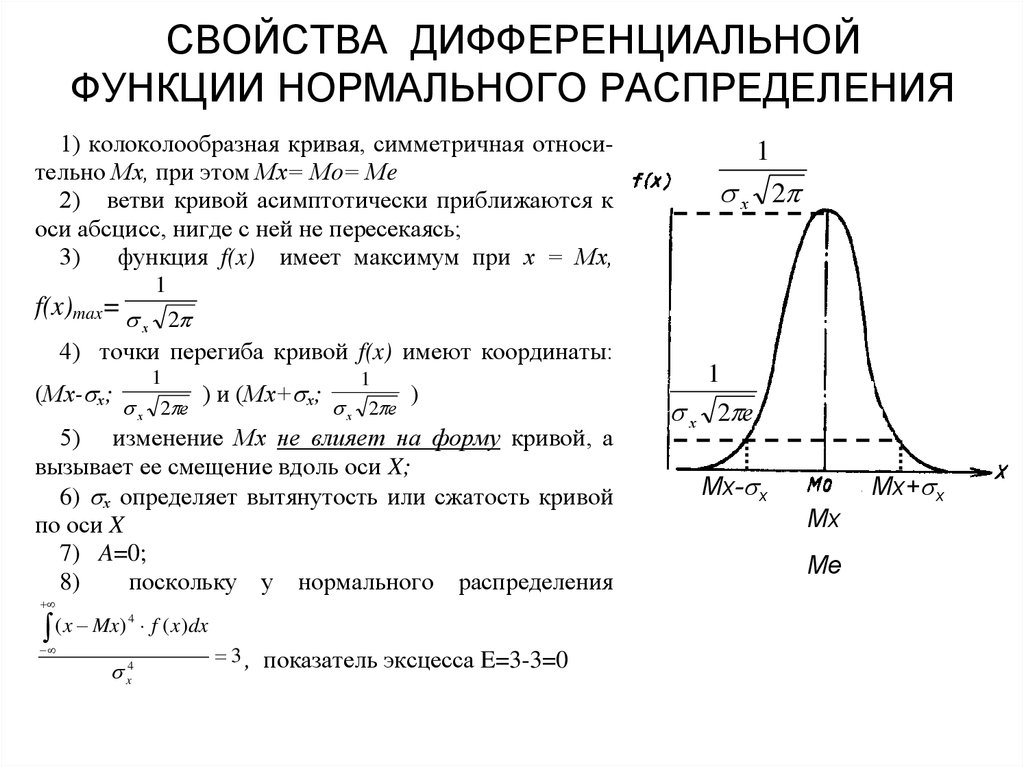 Приложение 1).
Приложение 1).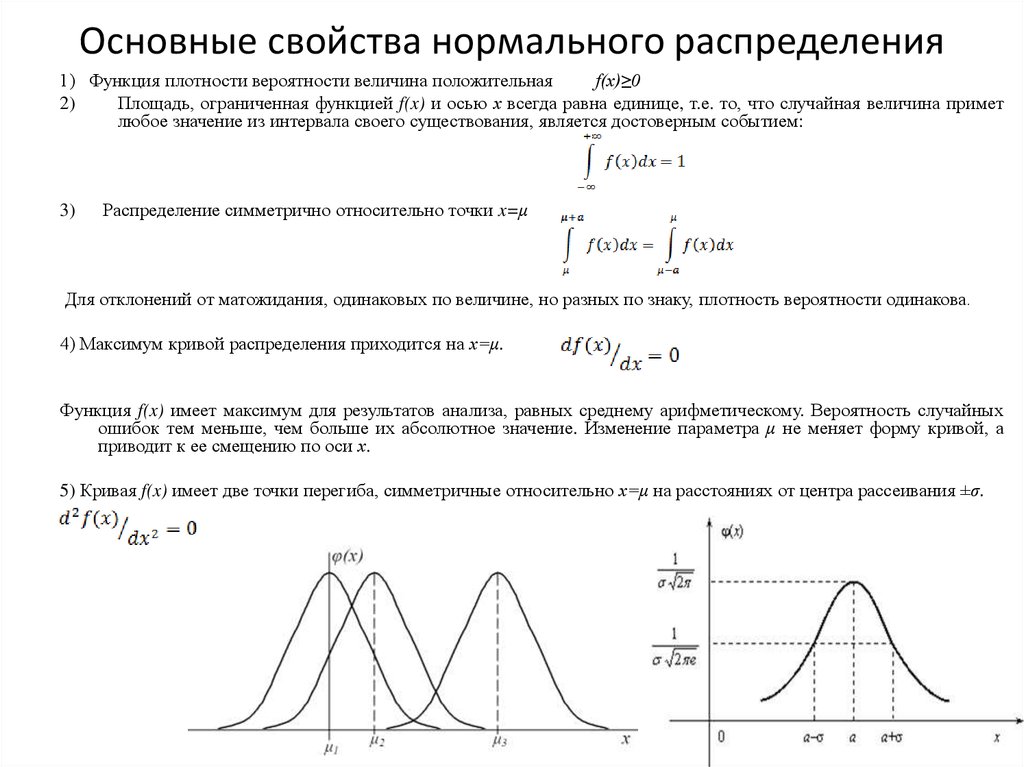 (Вероятность выхода за эти границы составляет
0,0027.) Правило позволяет, зная параметры ( и ), ориентировочно определить интервал практических
значений случайной величины.
(Вероятность выхода за эти границы составляет
0,0027.) Правило позволяет, зная параметры ( и ), ориентировочно определить интервал практических
значений случайной величины.

 В функции НОРМОБР
для поиска применяется метод итераций. Если поиск не закончился после 100
итераций, функция возвращает значение ошибки #Н/Д.
В функции НОРМОБР
для поиска применяется метод итераций. Если поиск не закончился после 100
итераций, функция возвращает значение ошибки #Н/Д.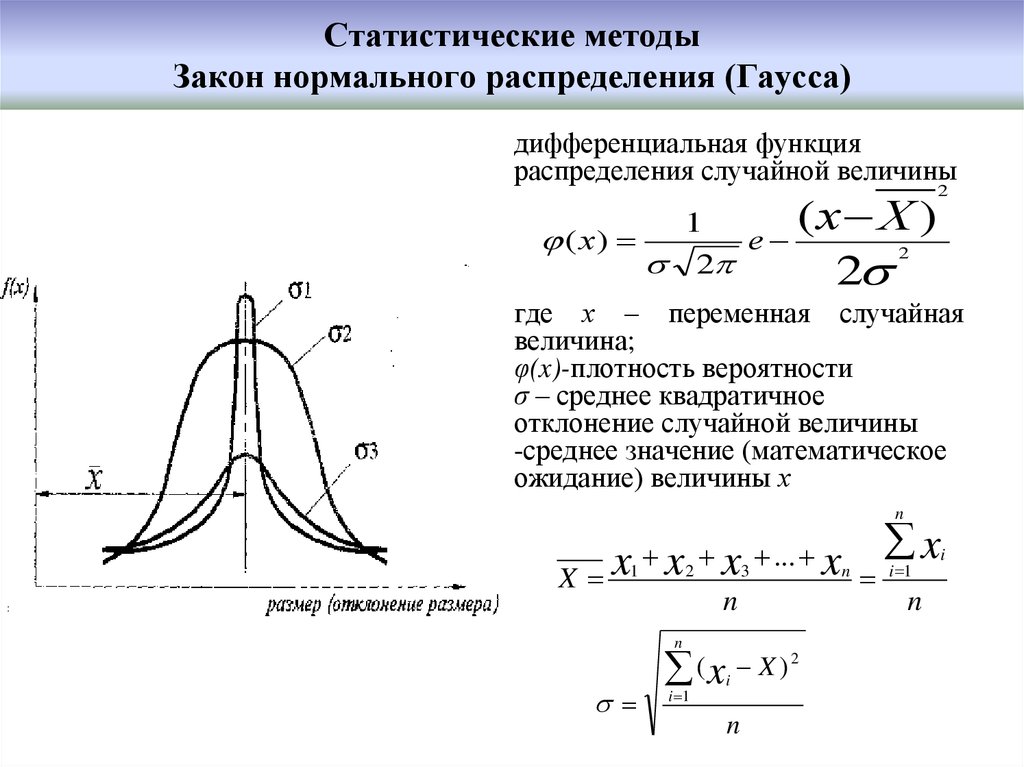
 pdf(x),
... 'r-', lw=5, альфа=0,6, метка='норма pdf')
pdf(x),
... 'r-', lw=5, альфа=0,6, метка='норма pdf')