Функция y 1 3x: Mathway | Популярные задачи — Таловская средняя школа

3 построить график и исследовать функцию

Содержание

Ответы

Михаил Александров

18.

05.17

Евгений

от 0 p.

Читать ответы

Лилия

Читать ответы

Андрей Андреевич

от 70 p.

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение

Решено

Радиус вписанной в квадрат окружности равен 4√2 найти радиус окружности описанной около этого квадрата

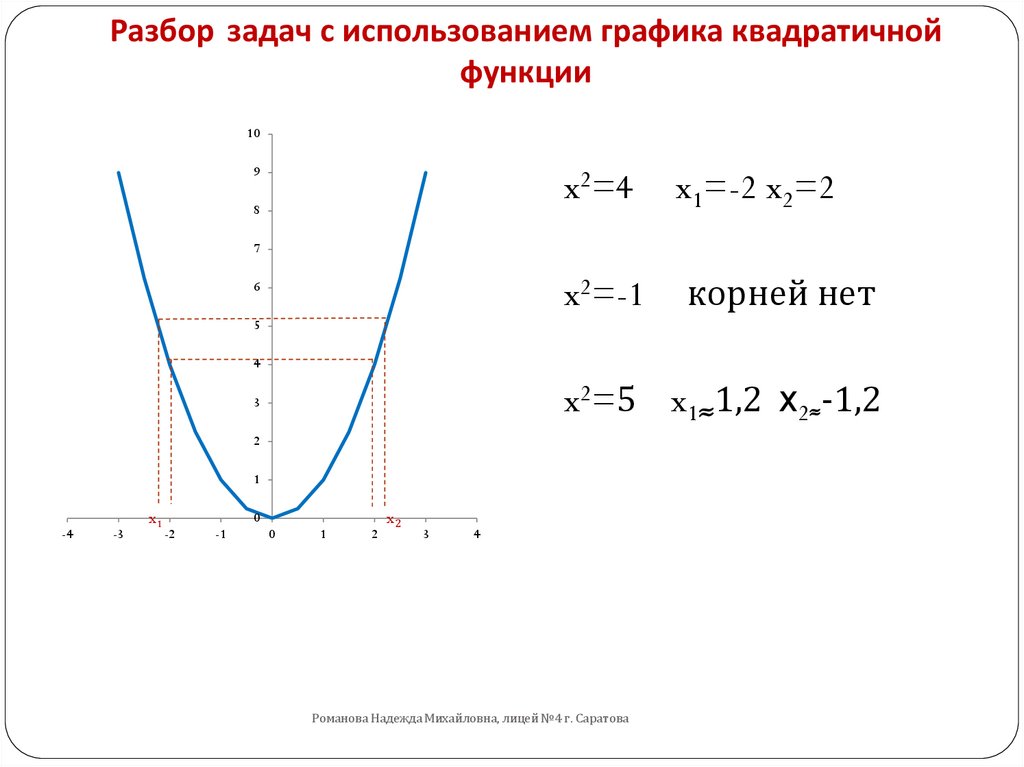
Постройте график функции y=x^2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные

Решено

В правильной четырёхугольной пирамиде диагональ основания равна 8 корней из 2 см, а двугранный угол при основании равен 60. 3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x).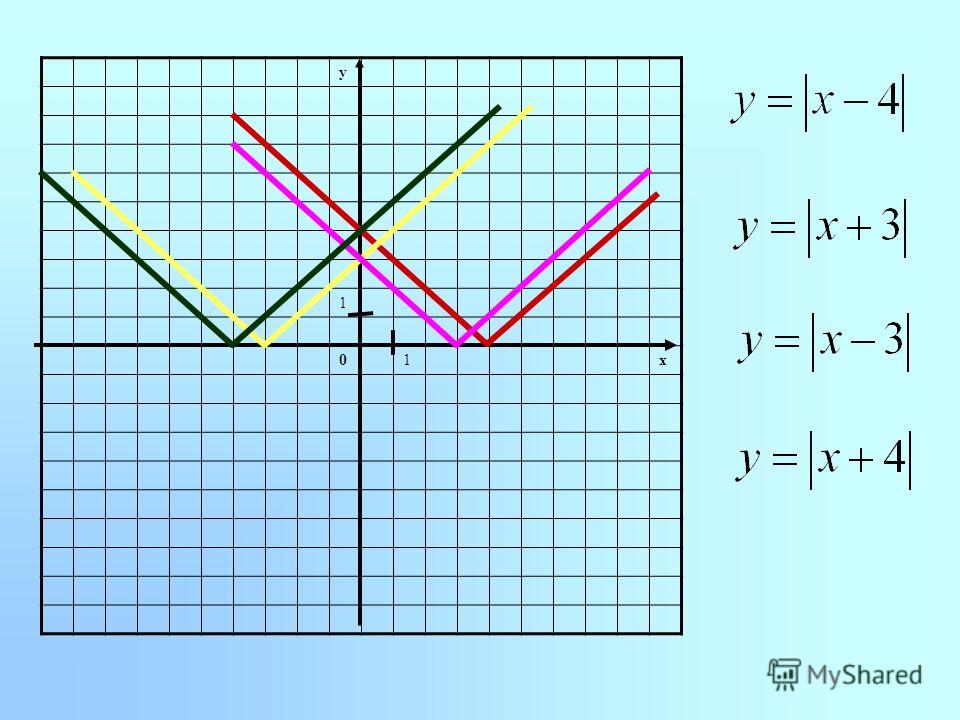 Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3)

(рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.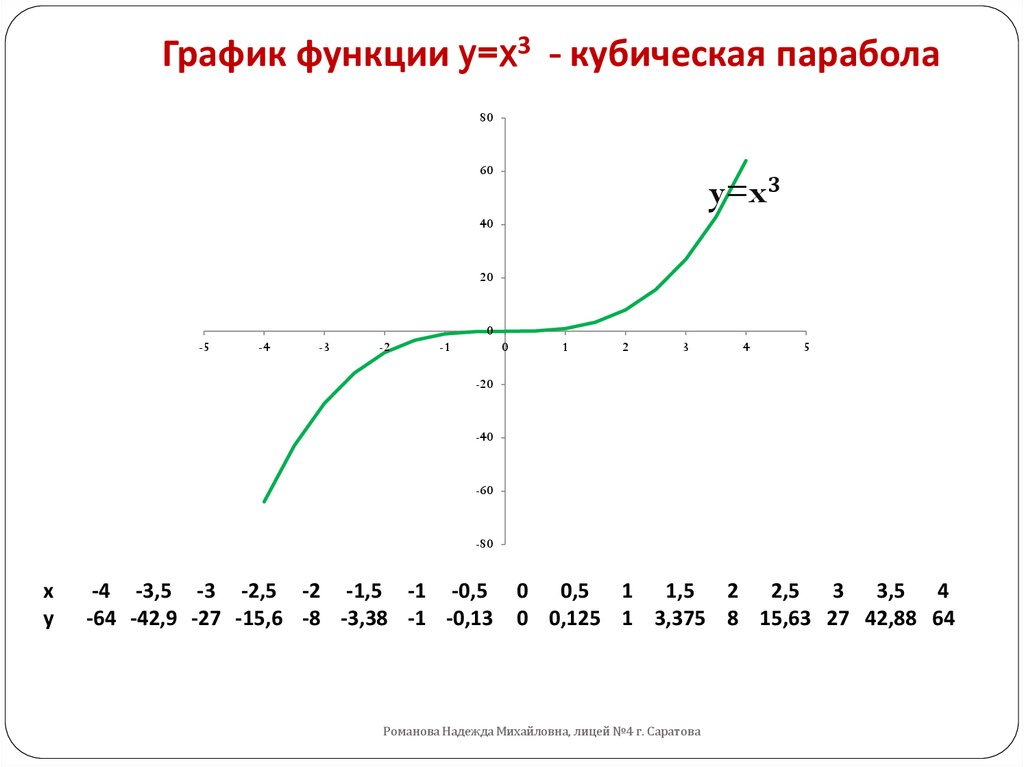

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа

f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис.

47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению

y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

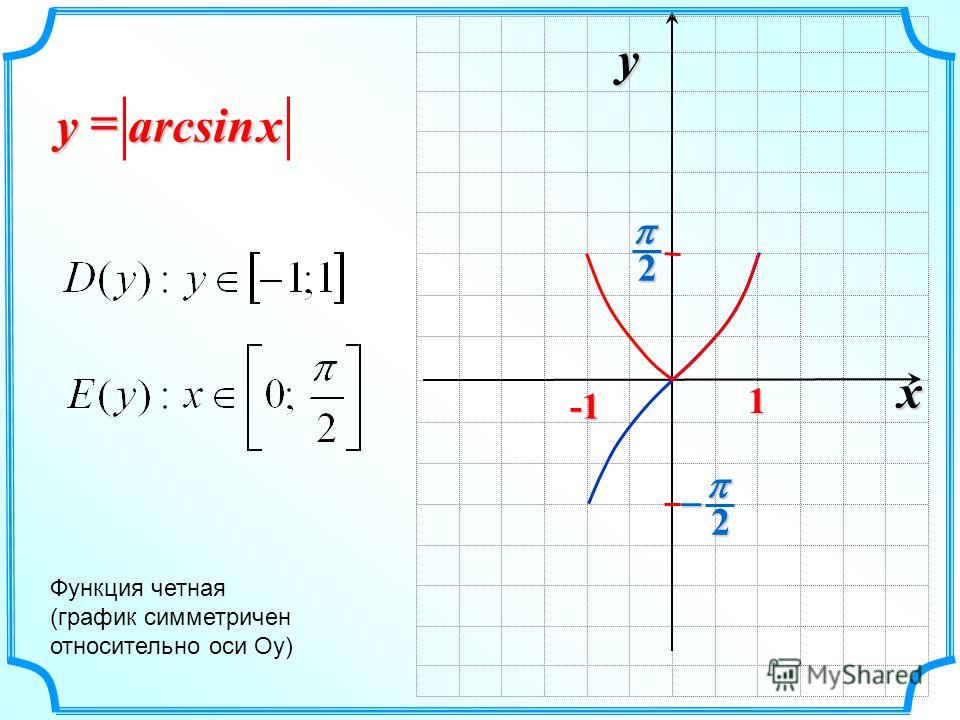
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.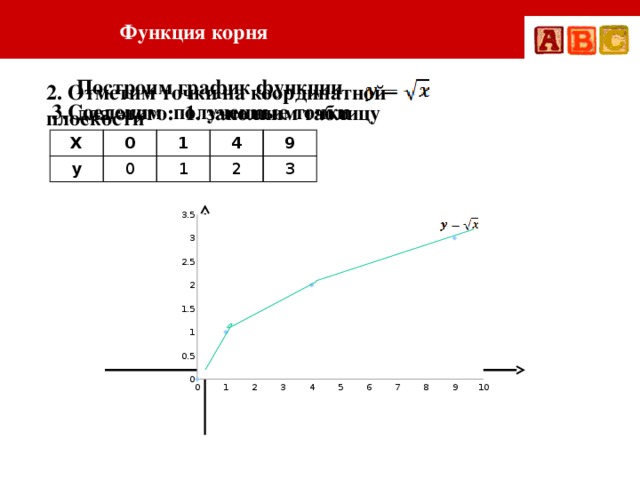

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Как найти уравнение перпендикулярной прямой

Все математические ресурсы SAT

16 Диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

SAT Math Help » Геометрия » Координатная геометрия » Линии » Перпендикулярные линии » Как найти уравнение перпендикулярной прямой

Уравнение прямой p равно y= 1/4x +6. Если прямая k содержит точку (3,5) и перпендикулярна прямой p , найдите уравнение прямой k.

у = -4х + 17

Объяснение:

Используя формулу пересечения наклона, мы видим, что наклон линии p равен ¼. Поскольку линия k перпендикулярна линии p, она должна иметь обратный отрицательный наклон. (-4/1) Если мы установим формулу y=mx+b, используя заданную точку и наклон (-4), мы можем решить для нашего пересечения b или y. В этом случае это будет 17,9.0911

Сообщить об ошибке Если линия B перпендикулярна A в точке (3,1), каково уравнение линии?

Возможные ответы:

y = -3x + 10

y = -3x + 1

y = 3x + 1

y = -1/3x + 10 9/9 8 9091 9091

Правильный ответ:

у = -3х + 10

Объяснение:

Во-первых, вам нужно получить уравнение первой линии, A.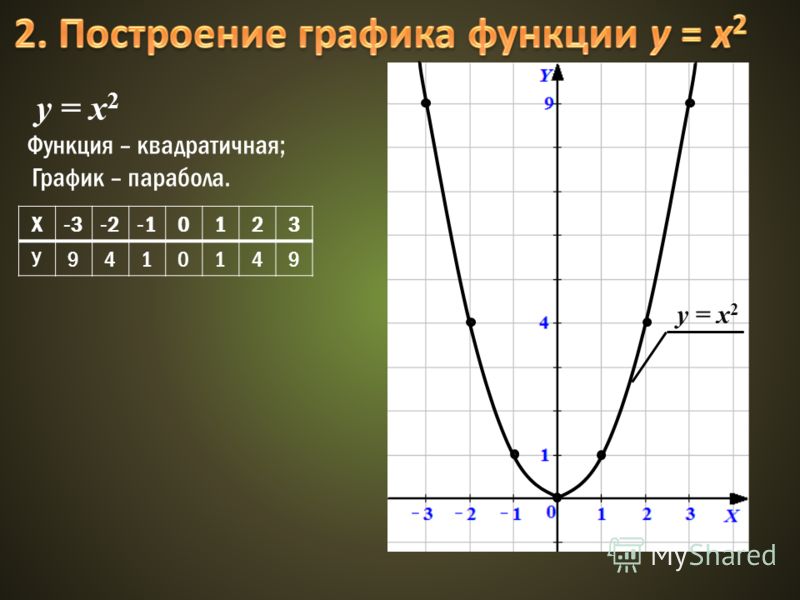 Его наклон определяется как:

(y ₂ — y ₁ ) / (x ₂ — x ₁ ) = (1 — 0) / (3 — 0) = 1/3 = наклон A.

Помните, что наклон перпендикулярной линии к данной линии в -1 раз больше, чем его наклон. Таким образом, наклон B:

(-1) x 1 / (1/3) = -3

Таким образом, с y = mx + b, m = -3. Теперь строка должна содержать (3,1). Таким образом:

с y = -3x + b:

1 = -3(3) + b;

1 = -9 + b; прибавьте 9 к обеим сторонам:

10 = b

Сообщить об ошибке

Какая прямая перпендикулярна прямой 2x + 3y = 6, проходящей через (4, 1)?

Возможные ответы:

2x + 3y = –5

3x + 2y = 10

–3x + 2y = –10

–x + 4y = 8

–2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2 –2

— x + 4y = 8

–10909

— x + 4y = 8

. Правильный ответ:

–3x + 2y = –10

Объяснение:

Данное уравнение имеет стандартную форму, поэтому его необходимо преобразовать в форму пересечения наклона: y = mx + b, чтобы определить, что наклон равен –2/3. Чтобы быть перпендикулярным, новый уклон должен составлять 3/2 (противоположная величина, обратная старому уклону). Используя новый наклон и заданную точку, мы можем подставить эти значения обратно в форму пересечения наклона, чтобы найти новое пересечение, -5. В форме пересечения наклона новое уравнение имеет вид y = 3/2x – 5. Правильным ответом является преобразование этого уравнения в стандартную форму.

Сообщить об ошибке

Концы отрезка AB расположены в точках (5, –2) и (–3, 10). Каково уравнение прямой, являющейся серединным перпендикуляром к AB?

Возможные ответы:

3x — 4y = –4

3x — 4y = –13

2x — 3y = –20

2x — 3y = –10

908 2 2x

99999999999999999999999999999999999999999999999999999999999999999999999999199999999999999999999999999999919.9097 2. ответ:

2x – 3y = –10

Пояснение:

Нас просят найти уравнение прямой, являющейся серединным перпендикуляром к AB.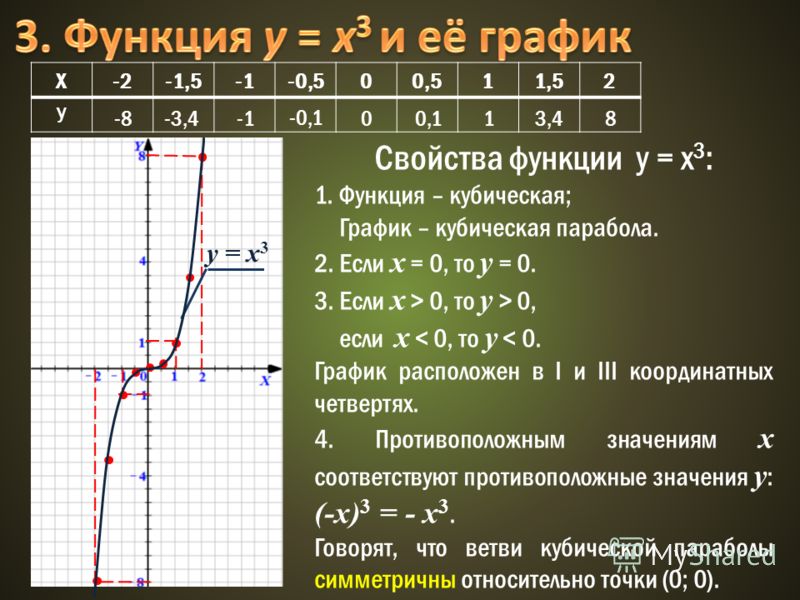 Если мы найдем точку, через которую проходит линия, а также ее наклон, мы сможем определить ее уравнение. Чтобы прямая делила AB пополам, она должна проходить через середину AB. Таким образом, одна точка на прямой является серединой АВ. Мы можем использовать формулу средней точки, чтобы определить середину AB с конечными точками (5, –2) и (–3, 10).

Координата x средней точки расположена в точке (5 + –3)/2 = 1,

Координата y средней точки расположена в точке (–2 + 10)/2 = 4,

Таким образом, середина AB равна (1, 4).

Итак, мы знаем, что прямая проходит через (1,4). Теперь мы можем использовать тот факт, что линия перпендикулярна AB, чтобы найти ее наклон. Произведение наклонов двух перпендикулярных отрезков равно –1. Другими словами, если мы умножим наклон линии на наклон AB, мы получим -1.

Мы можем использовать формулу наклона, чтобы найти наклон AB.

наклон AB = (10 – (–2))/(–3 – 5) = 12/–8 = –3/2.

Поскольку наклон линии, умноженный на –3/2, должен равняться –1, мы можем написать следующее:

(наклон линии)(–3/2) = –1

Если мы умножим обе части на –2/3, найдем наклон прямой.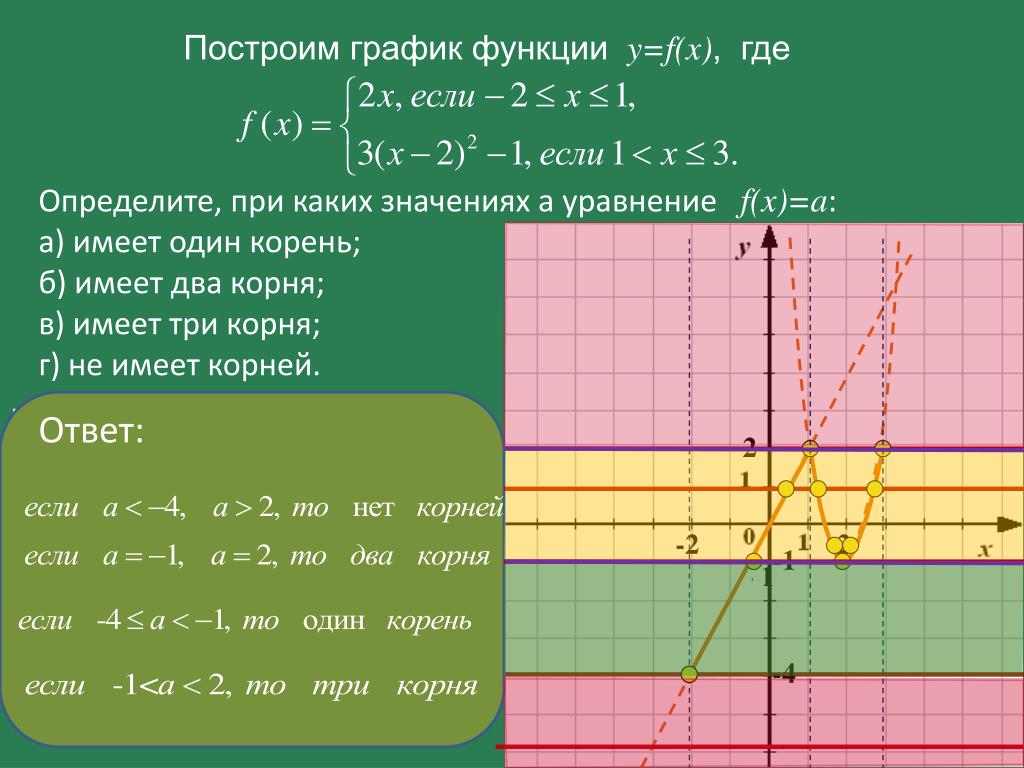

Наклон линии = (–1)(–2/3) = 2/3.

Таким образом, линия проходит через точку (1, 4) и имеет уклон 2/3.

Теперь мы будем использовать форму точка-наклон, чтобы определить уравнение линии. Пусть m представляет наклон, а (x ₁ , y ₁ ) представляет точку на линии.

y – y = m(x – x ₁ )

y – 4 = (2/3)(x – 1)

Умножьте обе части на 3, чтобы избавиться от дроби.

3(y – 4) = 2(x – 1)

Распределите обе стороны.

3y – 12 = 2x – 2

Вычтите 3y с обеих сторон.

–12= 2x – 3y – 2

Добавьте по 2 с обеих сторон.

–10 = 2x – 3y.

Уравнение прямой: 2x – 3y = –10.

Ответ: 2x – 3y = –10.

Сообщить об ошибке

Линия проходит через (2, 8) и (4, 15). Какое возможное уравнение для прямой, перпендикулярной этой?

Возможные ответы:

y = (8/3)x + 4

y = (–7/2)x + 4

Ни один из других ответов

y = (–2/7)x + 4

у = (2/7)х + 4

Правильный ответ:

у = (–2/7)х + 4

Пояснение:

Помните, перпендикулярные прямые имеют противоположно-обратные наклоны; поэтому давайте сначала найдем наклон нашей линии. Это находится по уравнению: рост/бег или y ₂ – y ₁ /x ₂ – x ₁

Подставив в наши значения: (15 – 8)/(4 – 2) = 7 /2

Таким образом, перпендикулярный уклон равен –2/7.

Так как ЛЮБАЯ перпендикулярная прямая пересекается с этой прямой в какой-то точке. Нам просто нужно выбрать ответ, у которого есть линия с наклоном -2/7. Следуя форме пересечения наклона (y = mx + b), мы знаем, что коэффициент x даст нам это; поэтому наш ответ таков: y = (–2/7)x + 4

Сообщить об ошибке

Линия p задается уравнением y = – x + 4. Какое из следующих уравнений описывает прямую, перпендикулярную p ?

Possible Answers:

y = –4

y = x + 4

x + y = –4

x + y = 4

y = – x – 4

Правильный ответ:

у = х + 4

Объяснение:

Уравнение линии p задается в виде y = m x + b , где м — наклон, а b — точка пересечения y — 90.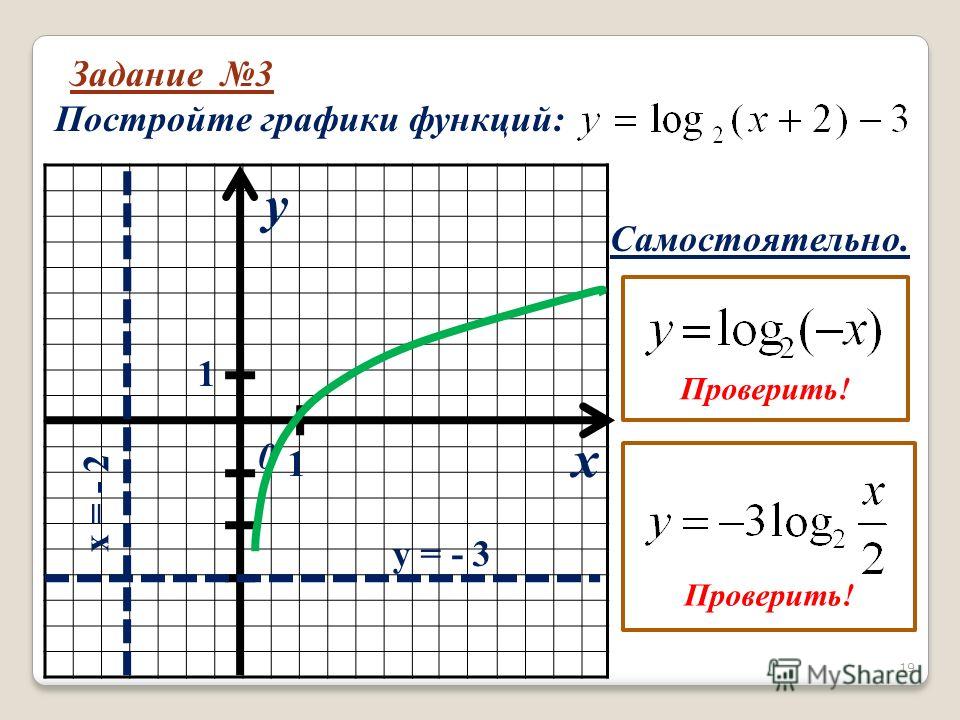 Поскольку уравнение имеет вид y = – x + 4, уклон составляет м = –1.

Если две прямые перпендикулярны, то произведение их наклонов равно –1. Таким образом, если мы назовем n наклон линии, перпендикулярной линии p , то верно следующее уравнение: можно написать (–1) n = –1. Если мы разделим обе стороны на –1, то n = 1. Короче говоря, наклон линии, перпендикулярной линии p , должен быть равен 1. Мы ищем уравнение линии, наклон которой равен 1.

Разберем варианты ответов. Уравнение y = – x – 4 имеет вид y = m x + b (что называется точечно-наклонной формой), поэтому его наклон равен –1, а не 1. Таким образом, мы можем исключить этот выбор.

Далее посмотрим на строку х + у = 4. Эта строка имеет вид Ах + По = С , где А 912 и В , В являются константами.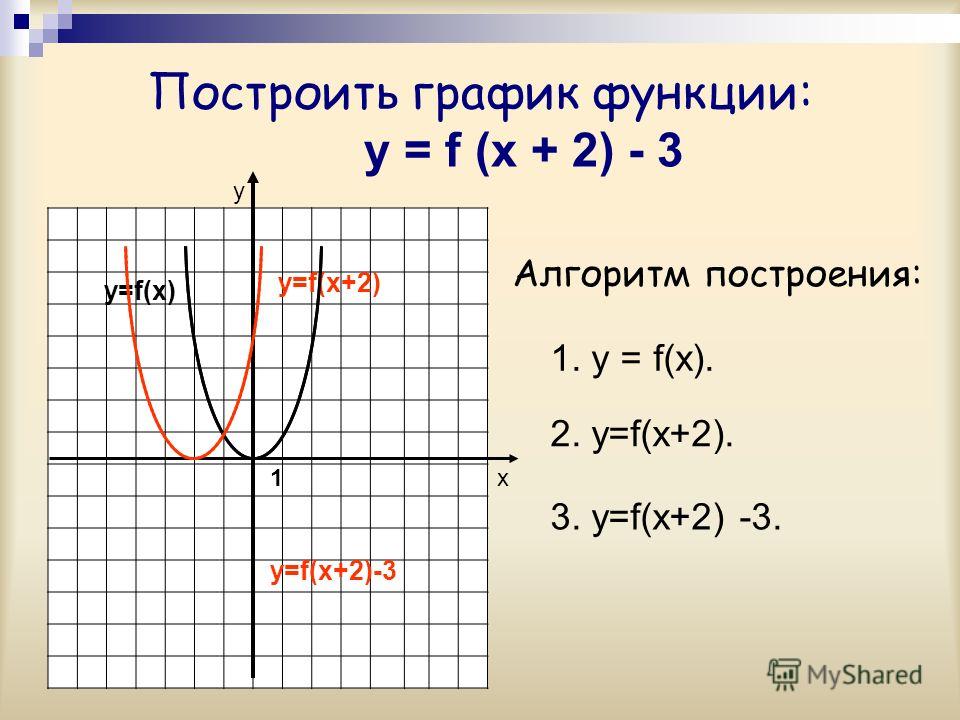 Когда линия имеет такую форму, ее наклон равен – A / Б . Следовательно, наклон этой линии равен –1/1 = –1, что не равно 1. Таким образом, мы можем исключить x + y = 4. Точно так же мы можем исключить линию x + . у = –4.

Линия y = –4 является горизонтальной линией, поэтому ее наклон равен 0, а не 1.

Ответом является прямая y = x + 4, потому что это единственная линия с наклоном 1.

Ответ: y = x + 4.

Сообщить об ошибке

Приведите уравнение прямой, перпендикулярной .

Возможные ответы:

Ни один из других ответов

Объяснение:

Наклон перпендикулярной линии обратно пропорционален, поэтому мы ищем линию с наклоном .

– единственный вариант ответа, удовлетворяющий этому критерию.

Сообщить об ошибке

Найдите уравнение прямой, перпендикулярной и проходящей через (5, 6).

Возможные ответы:

Правильный ответ:

Объяснение:

Мы знаем, что наклон исходной линии равен

Таким образом, наклон перпендикулярной линии является отрицательной обратной величиной , или –2.

Затем мы подставляем наклон и точку (5, 6) в форму , что дает

Если упростить, то получится

Сообщить об ошибке

Какая прямая проходит перпендикулярно через ?

Возможные ответы:

Правильный ответ:

Объяснение:

Нам нужно найти наклон заданного уравнения, преобразовав его в форму пересечения наклона: .

Наклон равен , а перпендикулярный наклон будет противоположным, обратным, или .

Новое уравнение имеет вид и мы можем использовать точку для вычисления . Следующим шагом является преобразование в стандартную форму .

Сообщить об ошибке

Какая прямая перпендикулярна и проходит через ?

Возможные ответы:

Правильный ответ:

Пояснение:

Перпендикулярные наклоны являются противоположными обратными величинами. Исходный наклон таков, что новый перпендикулярный наклон равен 3.

Мы подставляем точку и наклон в форму уравнения «точка-наклон»:

, чтобы получить или в стандартную форму .

Сообщить об ошибке

← Предыдущая 1 2 3 Следующая →

Уведомление об авторских правах

Все математические ресурсы SAT

16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept

В этом вопросе говорится построить график линейной функции.

y=1\3x-4. Как будет выглядеть график? В этом вопросе говорится построить график линейной функции.y=1\3x-4. Как будет выглядеть график?
Вопросы ООО
👤
🔎
Задать новый вопрос
Задавайте вопросы и получайте полезные ответы.
Задать новый вопрос
Спасибо, Рейни, но меня записали в этот класс, и я не могу понять, что делать. Когда я обращаюсь за помощью, они всегда заняты, чтобы помочь мне моей маме, когда разговаривают с директором, и она тоже не знает, что делать. Извините, что вынужден спросить.
👍
👎
👁
ℹ️
🚩
спросил синий
26 апреля 2015 г.
14 ответов
Ответы:
1.c
2.a
3.b
4. B
5. C
6. C
7. C
8. B
👍
👎
ℹ️
🚩
ответил фанат 5sos
30 января 2017 г.
Две точки образуют линию. Итак, что мы сделаем, так это получим любые 2 значения для x и получим соответствующее им значение y.
Например, возьмем x = 3.
Подставив это в линейное уравнение,
y = 1/3x — 4
y = 1/3 * 3 — 4
y = 1 — 4
y = -3
Следовательно, a точка на прямой равна (3,-3)
Еще одна точка, возьмем x = 6.
Замените:
y = 1/3x — 4
y = 1/3 * 6 — 4
y = 2 — 4
y = -2
Следовательно, точка на прямой равна (6,-2)
Теперь у вас есть точки (3,-3) и (6,-2). Возьмите графическую бумагу и нанесите эти точки. Соедините эти точки, продлите линию с обоих концов и нарисуйте стрелки на каждом конце.
Если вы все еще запутались, обратитесь к wolframalpha. com и введите «график y = 1/3x — 4». Он покажет вам график.
👍
👎
ℹ️
🚩
ответил Джай
26 апреля 2015 г.
‘Ладно, кто бы ни был здесь для юнит-теста, продолжайте искать какие-нибудь источники, чувак.
👍
👎
ℹ️
🚩
ответил after_sans7
2 мая 2021 г.
Вентилятор 5sos исправен!! 100%! Но тем, кто ищет ответы, БУДЬТЕ ОСТОРОЖНЫ!! В викторинах и тестах на готовность к алгебре много разных вопросов и ответов. так что просто перепроверьте.
👍
👎
ℹ️
🚩
ответил Спасибо!!
1 февраля 2017 г.
Спасибо за помощь.
👍
👎
ℹ️
🚩
ответил синим
26 апреля 2015 г.
он прав
👍
👎
ℹ️
🚩
ответил Pie почему
5 апреля 2017 г.
Кто-нибудь еще может подтвердить правильность 5sos?
👍
👎
ℹ️
🚩
ответил screee
21 мая 2018 г.
2 из ответов неверны 7 и 8
👍
👎
ℹ️
🚩
ответил Ханна
1 февраля 2019 г.
8/8 100%
👍
👎
ℹ️
🚩
ответил Верховный
7 февраля 2019 г.
..вы уверены, что 1 это c, потому что это противоречит тому, что у меня есть. Я получил B для 1, но опять же я не знаю, что я делаю. Но я не понимаю, как это c.
👍
👎
ℹ️
🚩
ответил Дастин
4 марта 2021 г.
Ладно, неважно, я просто вставил их ответы и получил 8/8. Спасибо!
👍
👎
ℹ️
🚩
ответил Дастин
4 марта 2021 г.
ок без 7
👍
👎
ℹ️
🚩
ответил Странный парень:()
10 мая 2021 г.
Вентилятор 5sos верен клянусь жизнью
👍
👎
ℹ️
🚩
ответил Аноним
8 марта 2022 г.
7 is D 8 is c i jsut я обещаю, я не лгу, меня учили не лгать
👍
👎
ℹ️
🚩
ответил Привет
25 мая 2019 г.
No related posts.