Функция y 2 x и ее график: Построить график функций y=2/x — ответ на Uchi.ru

Линейная функция. Линейная функция Построить график линейной функции y 3

Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.

В частном случае, если k = 0 , получим постоянную функцию y = b , график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b) .

Если b = 0 , то получим функцию y = kx , которая является прямой пропорциональностью.

b – длина отрезка , который отсекает прямая по оси Oy, считая от начала координат.

Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.

Свойства линейной функции:

1) Область определения линейной функции есть вся вещественная ось;

2) Если k ≠ 0 , то область значений линейной функции есть вся вещественная ось. Если k = 0 , то область значений линейной функции состоит из числа b ;

3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b .

a) b ≠ 0, k = 0, следовательно, y = b – четная;

b) b = 0, k ≠ 0, следовательно y = kx – нечетная;

c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;

d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.

4) Свойством периодичности линейная функция не обладает;

5) Точки пересечения с осями координат:

Ox: y = kx + b = 0, x = -b/k , следовательно (-b/k; 0) – точка пересечения с осью абсцисс.

Oy: y = 0k + b = b , следовательно (0; b) – точка пересечения с осью ординат.

Замечание.Если b = 0 и k = 0 , то функция y = 0 обращается в ноль при любом значении переменной х .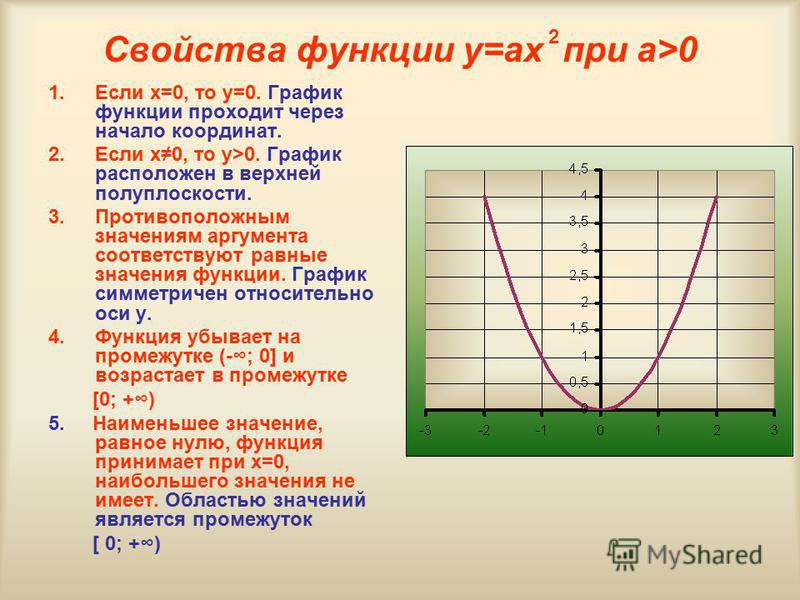 Если b ≠ 0 и k = 0 , то функция y = b не обращается в ноль ни при каких значениях переменной х .

6) Промежутки знакопостоянства зависят от коэффициента k.

a) k > 0; kx + b > 0, kx > -b, x > -b/k.

y = kx + b – положительна при x из (-b/k; +∞) ,

y = kx + b – отрицательна при x из (-∞; -b/k) .

b) k

y = kx + b – положительна при x из (-∞; -b/k) ,

y = kx + b – отрицательна при x из (-b/k; +∞) .

c) k = 0, b > 0; y = kx + b положительна на всей области определения,

k = 0, b отрицательна на всей области определения.

7) Промежутки монотонности линейной функции зависят от коэффициента k .

k > 0 , следовательно y = kx + b возрастает на всей области определения,

k , следовательно y = kx + b убывает на всей области определения.

8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.

Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.

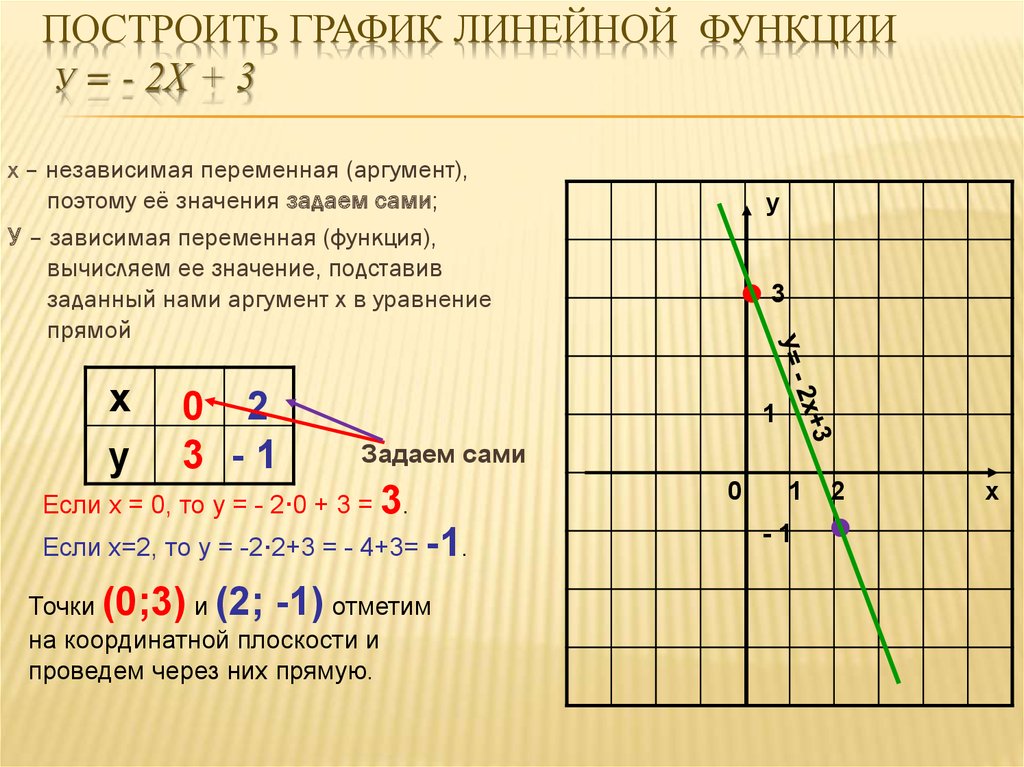
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции y= ⅓ x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓ x+2:

2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½ x+3; y=x+3

Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3

На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3; y=2x; y=2x-3

Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.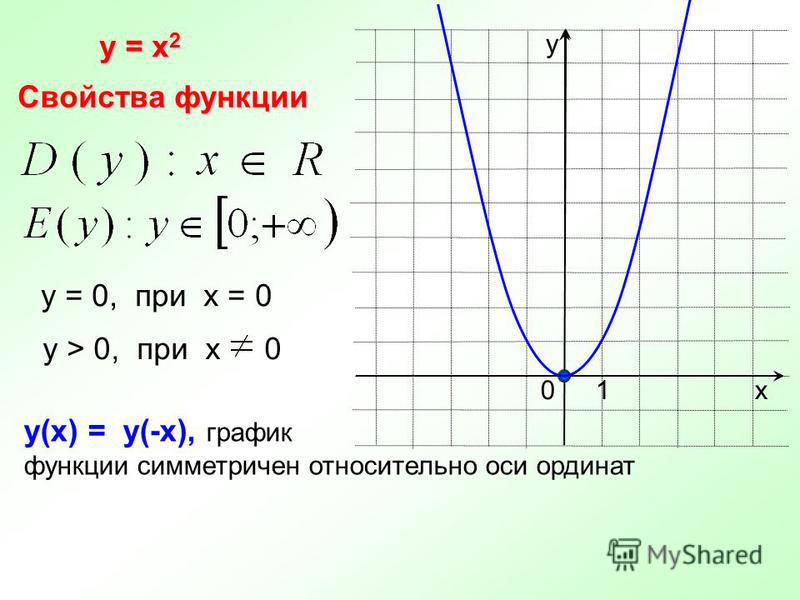

Если k 0

Если k>0 и b>0 , то график функции y=kx+b имеет вид:

Если k>0 и b , то график функции y=kx+b имеет вид:

Если k, то график функции y=kx+b имеет вид:

Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:

3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.

Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2

5.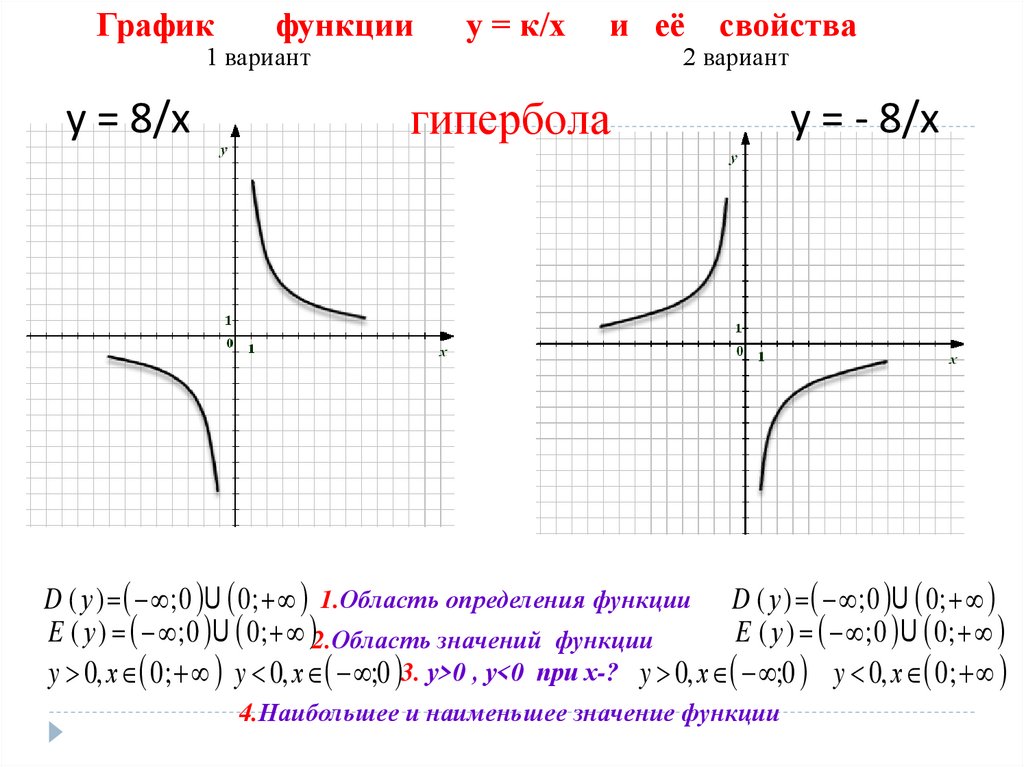 Условие перепендикулярности двух прямых:

График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2

6. Точки пересечения графика функции y=kx+b с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):

Определение линейной функции

Введем определение линейной функции

Определение

Функция вида $y=kx+b$, где $k$ отлично от нуля называется линейной функцией.

График линейной функции — прямая. Число $k$ называется угловым коэффициентом прямой.

При $b=0$ линейная функция называется функцией прямой пропорциональности $y=kx$.

Рассмотрим рисунок 1.

Рис. 1. Геометрический смысл углового коэффициента прямой

Рассмотрим треугольник АВС. Видим, что$ВС=kx_0+b$. Найдем точку пересечения прямой $y=kx+b$ с осью $Ox$:

\ \

Значит $AC=x_0+\frac{b}{k}$. Найдем отношение этих сторон:

\[\frac{BC}{AC}=\frac{kx_0+b}{x_0+\frac{b}{k}}=\frac{k(kx_0+b)}{{kx}_0+b}=k\]

С другой стороны $\frac{BC}{AC}=tg\angle A$.

Таким образом, можно сделать следующий вывод:

Вывод

Геометрический смысл коэффициента $k$. Угловой коэффициент прямой $k$ равен тангенсу угла наклона этой прямой к оси $Ox$.

Вначале рассмотрим функцию $f\left(x\right)=kx+b$, где $k > 0$.

1. $f»\left(x\right)={\left(kx+b\right)}»=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
2. ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
3. График (рис. {«»}\left(x\right)=k»=0$. Следовательно, функция не имеет точек перегиба.
4. ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
5. График (рис. 3).

ГДЗ Алгебра Александрова 8 класс Самостоятельные Топ

Подробные решения по алгебре за 8 класс авторы Александрова

Заблаговременная подготовка к проверочной — отличная идея для получения высокой оценки за работу с минимумом усилий для достижения этой цели. Чтобы все складывалось максимально удачно, рекомендуется воспользоваться специализированным справочником-помощником. В числе наиболее грамотных и эффективных при решении этих задач называют гдз по алгебре за 8 класс самостоятельные работы Александрова — при условии правильной работы с ними. Слагаемыми успеха признаются ежедневные часовые занятия и отсутствие продолжительных, сверх 10 дней подряд, пропусков в них. Это позволит не забыть большую часть проработанного материала, успешно написать самостоятельную в классе, получив высокий балл, избежать усталости. Плюс — приобрести глубокие и полные знания по дисциплине.

Кто и для чего использует онлайн помощники в учебном процессе?

Среди тех, кто системно и регулярно применяет подробные решения по алгебре 8 класс для самостоятельных работ Александрова — такие группы пользователей:

• восьмиклассники, по тем или иным причинам часто пропускающие занятия (дети, которые часто болеют, профессиональные спортсмены, выезжающие на сборы и соревнования, творческие личности, участвующие во всевозможных конкурсах и пр.). Для них сборник станет источником для получения нужных знаний, позволяющих им правильно написать проверочную;
• подростки, переведенные на дистанционную форму образования, избравшие домашний/семейный формат обучения. В этом случае материалы позволят дополнить объяснение учителя и получить на проверке хорошую отметку;
• педагоги-предметники, которым надо оперативно проверить большое количество сданных школьниками работ. Ресурс поможет им сэкономить время на решение срочных дел (плановых, отчетных и т. д.), не рискуя качеством результата;
• родители восьмиклассников, справедливо полагающие, что приведенные ответы позволят им проверить степень готовности своего ребенка к предстоящим в школе проверочным. При этом — не вникать глубоко в суть программы, в темы и разделы школьного алгебраического курса.

Очевидные преимущества применения ответов к самостоятельным работам по алгебре за 8 класс (автор Александрова)

Правда, некоторые родители и учителя до сих пор не оценили всех преимуществ еуроки ГДЗ, считая, что подростки просто бездумно списывают с них готовые решения. Но это совсем не так. Польза у ресурса огромна:

• он доступен в любое время и всем;
• при возникновении сложностей с решением всегда можно найти здесь подсказку, проработать задание еще до того, как за его выполнение будут ставить оценку в классе;
• вся информация представлена в соответствии с действующими образовательными Стандартами, включая требования к оформлению;
• это экономически выгодное решение, позволяющее сократить расходы на репетиторов или даже полностью отказаться от них.

Применяя сборник готовых решений, школьники учатся работать со справочной литературой в условиях ограниченного времени на выполнение задачи. Этот ценный навык пригодится им и сейчас, и впоследствии.

(-x) показано на рисунке. Какова ценность а? ltimg src=»https://d10lpgp6xz60nq.cloudfront.net/physicsimages/ALNPHYR04E01028Q01.png»gt

ALLEN-RACE-Basic Maths (Graphs))

20 videos

ADVERTISEMENT

Ab Padhai karo bina ads ke

Khareedo DN Про и дехо сари видео бина киси объявление ки rukaavat ке!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

Стенограмма

график экспоненциальной функции Y равен 2 + 8 степень минус 6 известно каково значение уравнения вы дали график найдите значение первого если мы наблюдаем этот график в точке Это значение x и y задано X будет равно нулю, тогда почему будет значение в ситуации, поэтому мы получим Y равно 2 + a e в степени минус 6 значение Y

хорошо, так что будет 6 равно 2 + a равно 8. 0 какое будет видео что будет 6 равно 2 + а найдите значение е в степени минус один что означает а равно 6 — 2 это будет значение ок спасибо

---

Похожие видео

Сопоставьте следующий столбец A со столбцом B

42341958

Сопоставьте следующий столбец A со столбцом B

42341959 Сопоставьте следующий столбец B

90

42342014

Найдите площадь фигуры, приведенной ниже.

43957973

Найдите периметр фигуры, приведенной ниже.

43958020

Найдите площадь фигуры, приведенной ниже.

43958043

Площадь заштрихованной части на приведенном ниже рисунке равна ______.

43958096

На рис. найдите значение x.
ltimg src = «https://d10lpgp6xz60nq. cloudfront.net/physics_images/ps_math_ix_c12_s01_032_q01.png» gt

46934026

. net/physics_images/ALN_PHY_R04_E01_020_Q01.png»gt

48209751

При x=0 значение (dy)/(dx): ltimg src=»https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png»gt

48209755

Каково расстояние OA для квадрат, показанный на рисунке: — ltimg src=»https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_015_Q01.png»gt

48209787

.cloudfront.net/physics_images/ALN_PHY_R05_E01_035_Q01.png»gt

48209814

Найдите величину равнодействующей показанных сил:-
ltimg src=»https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R02_E02_009_Q01.png»gt

48209874

3 Из следующего наблюдения правильно :- ltimg src=»https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E08_015_Q01.png»gt

48210384

Общая площадь поверхности данной объемной фигуры _______________.