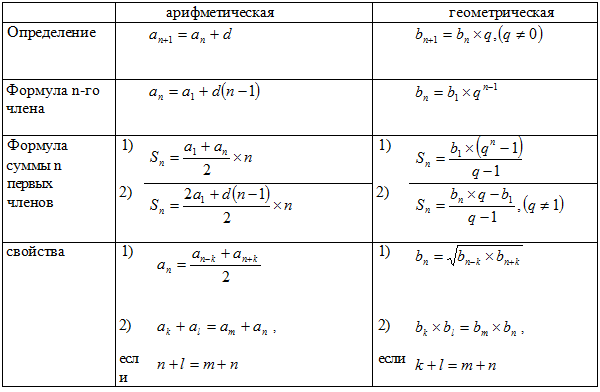Вся элементарная математика — Средняя математическая интернет-школа
Числовая последовательность. Арифметическая прогрессия.
Разность прогрессии. Геометрическая прогрессия. Знаменатель
прогрессии. Бесконечно убывающая геометрическая прогрессия.
Обращение периодической десятичной дроби в обыкновенную.
Последовательности. Рассмотрим ряд натуральных чисел:
1, 2, 3, … , n – 1, n , … .
Если заменить каждое число n в этом ряду некоторым числом u n , следуя некоторому закону, мы получим новый ряд чисел:
u
называемый числовой
последовательностью .
Число u n называется общим членом числовой последовательности.
П р и м е р ы числовых последовательностей:
2, 4, 6, 8, 10, … , 2 n , … ;
1, 4, 9, 16, 25, … , n ² , … ;
1, 1/2, 1/3, 1/4, 1/5, … , 1/ n , … .
Арифметическая прогрессия. Числовая
последовательность,
каждый член которой, начиная со
второго, равен предыдущему, сложенному с постоянным для этой последовательности
числом d , называется арифметической прогрессией . Число d называется разностью
прогрессии .
Любой член ариф
метической
прогрессии вычисляется по формуле:
Сумма n первых членов арифметической прогрессии вычисляется как:
П р и м е р . Найти сумму первых ста нечётных чисел.
Р е ш е н и е . Применим последнюю формулу. Здесь a 1 = 1, d = 2 . Тогда
Геометрическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической
прогрессией .
Число q называется знаменателем
прогрессии . Любой член
геометрической прогрессии вычисляется
по формуле:
b n = b 1 q n — 1 .
Сумма n первых членов геометрической прогрессии вычисляется как:
Бесконечно убывающая геометрическая прогрессия.
которому неограниченно приближается
сумма n первых членов рассматри
ваемой
прогрессии при неограниченном возрастании числа n .
Сумма
членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:
П р и м е р . Найти сумму членов бесконечно убывающей геометрической прогрессии:
Р е ш е н и е . Применим последнюю формулу. Здесь b 1 = 1, q = 1/2. Тогда:
Обращение периодической
десятичной дроби в обыкновенную. Предположим, мы хотим обратить
периодическую десятичную дробь 0.
(3) в
обыкновенную. Рассмотрим эту десятичную дробь в следующем виде:
Это бесконечно убывающая геометрическая прогрессия, первый член которой равен 3/10, а разность q = 1/10. В соответствии с выше приведенной формулой эта сумма равна:
Таким образом , 0.(3) = 1/3.
Назад
Алгебра: Арифметическая и геометрическая прогрессии
4.
Арифметическая и геометрическая прогрессии
Теоретические сведения
Теоретические сведения
Определение |
Арифметической прогрессией an называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d (d — разность прогрессий) |
Геометрической прогрессией bn называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число q (q — знаменатель прогрессии) |
Рекуррентная формула |
Для любого натурального n |
Для любого натурального n |
Формула n-ого члена |
an = a1 + d ( n – 1) |
bn = b1 ∙ qn — 1, bn ≠ 0 |
| Характеристическое свойство | ||
| Сумма n-первых членов |
Примеры заданий с комментариями
Задание 1
В арифметической прогрессии (an
) a1
= -6, a2
= -8.
Найдите двадцать второй член прогрессии.
Решение
По формуле n-ого члена:
a22 = a 1 + d (22 — 1) = a1 + 21 d
По условию:
a1 = -6, значит a22 = -6 + 21 d.
Необходимо найти разность прогрессий:
d = a2 – a1 = -8 – (-6) = -2
a22 = -6 + 21 ∙ (-2) = — 48.
Ответ: a22 = -48.
Задание 2
Найдите пятый член геометрической прогрессии: -3; 6;….
Решение
1-й способ (с помощью формулы n -члена)
По формуле n-ого члена геометрической прогрессии:
b5 = b1 ∙ q5 — 1 = b1 ∙ q4 .
Так как b1 = -3,
а
2-й способ (с помощью рекуррентной формулы)
Так как знаменатель прогрессии равен -2 (q = -2), то:
b3 = 6 ∙ (-2) = -12;
b4 = -12 ∙ (-2) = 24;
b5
= 24 ∙ (-2) = -48.
Ответ: b5 = -48.
Задание 3
В арифметической прогрессии (an ) a74 = 34; a76 = 156. Найдите семьдесят пятый член этой прогрессии.
Решение
Для арифметической прогрессии характеристическое свойство имеет вид .
Из этого следует:
.
Подставим данные в формулу:
Ответ: 95.
Задание 4
В арифметической прогрессии (an ) an = 3n — 4. Найдите сумму семнадцати первых членов.
Решение
Для нахождения суммы n-первых членов арифметической прогрессии используют две формулы:
.
Какую из них в данном случае удобнее применять?
По условию известна формула n-ого члена исходной прогрессии (an ) an = 3n — 4. Можно найти сразу и a1 , и a16 без нахождения d. Поэтому воспользуемся первой формулой.
Ответ: 368.
Задание 5
В арифметической прогрессии(an
) a1
= -6; a2
= -8.
Найдите двадцать второй член прогрессии.
Решение
По формуле n-ого члена:
a22 = a1 + d (22 – 1) = a1 + 21d.
По условию, если a1 = -6, то a22 = -6 + 21d. Необходимо найти разность прогрессий:
d = a2 – a1 = -8 – (-6) = -2
a22 = -6 + 21 ∙ (-2) = -48.
Ответ: a22 = -48.
Задание 6
Записаны несколько последовательных членов геометрической прогрессии:
Найдите член прогрессии, обозначенный буквой x.
При решении воспользуемся формулой n-го члена bn
= b1
∙ qn — 1
для геометрических прогрессий. Первый член прогрессии. Чтобы найти знаменатель прогрессии q необходимо взять любой из данных членов прогрессии и разделить на предыдущий. В нашем примере можно взять и разделить на. Получим, что q = 3. Вместо n в формулу подставим 3, так как необходимо найти третий член, заданной геометрической прогрессии.
Подставив найденные значения в формулу, получим:
.
Ответ: .
Задание 7
Из арифметических прогрессий, заданных формулой n-го члена, выберите ту, для которой выполняется условие a27 > 9:
1) ;
2) ;
3) ;
4) .
Так как заданное условие должно выполняться для 27-го члена прогрессии, подставим 27 вместо n в каждую из четырех прогрессий. В 4-й прогрессии получим:
.
Ответ: 4.
Задание 8
В арифметической прогрессии a1 = 3, d = -1,5. Укажите наибольшее значение n, для которого выполняется неравенство an > -6.
Решение
Воспользуемся формулой n-го члена.
an = a1 + d (n – 1) > -6.
Подставим данные в условии значения в формулу:
3 – 1,5n + 1,5 > -6
6 + 4,5 > 1,5n
n < 7
Ответ: Наибольшее значение n = 6.
Задание 9
В геометрической прогрессии сумма первого и второго членов равна 108, а третьего и четвертого — 168,75.
Найдите первых три члена прогрессии.
Решение
Составим систему уравнений:
Подставим b1 во второе уравнение:
Тогда:
.
Задание 10
Произведение первого и пятого членов геометрической прогрессии равно 4, а частное от деления пятого члена на седьмой равно 9. Найдите четвертый член этой прогрессии.
Решение
Составим систему уравнений:
При .
При .
При получим те же значения: .
При .
При получим те же значения .
Арифметико-геометрическая прогрессия | Brilliant Math & Science Wiki
Сандип Бхардвадж, Пранджал Джайн, Махиндра Джейн, и
способствовал
Содержимое
- Определение
- Сумма AGP
- Сумма AGP до бесконечности
- Приложения
- Смотрите также
Давайте начнем с нескольких простых определений понятий, которые мы будем неоднократно использовать.
2}.
\конец{выравнивание}\]
9{99}= \, ?\]
Теперь, когда мы нашли сумму конечного числа членов, давайте рассмотрим случай бесконечного числа членов. Мы, конечно, не можем вручную суммировать бесконечные члены, поэтому нам придется найти общий подход. Мы начинаем с обсуждения проблемы, с которой вы столкнулись, вверху этой страницы:
\[\ большой \dfrac{\color{blue}{1}}{\color{red}{2}}+\dfrac{\color{blue}{2}}{\color{red}{4}}+ \ dfrac {\ color {синий} {3}} {\ color {red} {8}} + \ dfrac {\ color {синий} {4}} {\ color {red} {16}} + \ dfrac {\ цвет{синий}{5}}{\цвет{красный}{32}}+\cdots=\, ?\]
Предположим, что данный ряд равен \(S\), тогда
\[S=\dfrac 12 +\dfrac 24 +\dfrac 38+\dfrac{4}{16}+\dfrac{5}{32}+\cdots.\]
Умножив \(S\) на \(\frac 12\), мы получим
\[ \dfrac S2=\dfrac 14 +\dfrac 28 +\dfrac{3}{16}+\dfrac{4}{32}+\dfrac{5}{64}+\cdots.\]
Теперь, вычитая \(\frac S2\) из \(S\), мы получаем
\[ \begin{массив} {rlllllllll} S&=\dfrac 12 &+\dfrac 24 &+\dfrac 38 &+\dfrac{4}{16} &+\dfrac{5}{32}+ \cdots \\ \dfrac S2&=0&+\dfrac 14 & +\dfrac 28 & +\dfrac{3}{16}&+\dfrac{4}{32}+\dfrac{5}{64}+\cdots \\ \hline S \left(1- \dfrac 12 \right)& =\dfrac 12& +\dfrac 14 & + \dfrac 18 & +\dfrac{1}{16} & +\dfrac{1}{32} +\cdots \ \ \Стрелка вправо \dfrac S2&=\dfrac 12 &+\dfrac 14 &+ \dfrac 18 &+\dfrac {1}{16} &+\dfrac {1}{32} +\cdots, \конец{массив}\] 92 } = 2 \).
Второе суммирование представляет собой геометрическую прогрессию с суммой до бесконечности \( \frac { \frac{1}{4} } { 1 — \frac{1}{2} } = \frac{1}{2} \ ).
Следовательно, сумма равна \( 2 — \frac{1}{2} = 1,5 \ _\square \).Решение 2:
Данную серию можно записать как
\[\dfrac 14+\dfrac 38 +\dfrac{5}{16}+\dfrac{7}{32}+\cdots .\]
Умножив и разделив ряд на \(4\), получим
\[ \dfrac{1}{4} \left( 1+\dfrac{3}{2}+ \dfrac{5}{4}+\dfrac{7}{8}+ \cdots \right) .\ ] 9п}=2. \ _\квадрат\)
Давайте посмотрим, сможете ли вы решить следующую задачу.
Если мы бросим один кубик, каково ожидаемое количество бросков, прежде чем мы получим первые 6?
Примечание: бросок 6 включен в «количество бросков, прежде чем мы получим первые 6».
\(\text{}\)
2. Расширение метода суммирования
\(\text{}\)
Вычислить \(\displaystyle\sum_{i=1}^\infty \frac{i^2} { 2^i } \).Пусть сумма будет \(S,\), тогда, поскольку обыкновенное отношение равно \( \frac{1}{2} \), мы умножим \(S\) на \( \frac{1}{2} . \) Вычитание \(\frac{1}{2}S\) из \(S\) дает
\[ \begin{array} { r lllllll}
S& =\frac 12 & +\frac {4}{4} & +\frac{9}{8} &+\frac{16}{16} &+ \frac{25}{32} &+\cdots \\ \frac{1}{2} S& = & + \frac 14 & +\frac {4}{8} & +\frac{9}{16} &+\frac{16}{32} &+\cdots \\ \hline \frac{1}{2} S & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9 }{32} &+\cdots .\\ \конец{массив} \]Мы можем распознать здесь AGP, но пусть \(T=\frac{1}{2} S\) и продолжим эту процедуру определения разницы:
\[ \begin{array} { r lllllll}
T & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} & +\frac{9}{32} &+\cdots \\
\frac{1}{2} T & = & + \frac 14 & +\frac {3}{8} & +\frac{5}{ 16} &+\frac{7}{32} &+\cdots \\
\hлиния \frac{1}{2} T & = \frac{1}{2} & + \frac{2}{4} & + \frac{2}{8} & + \frac{2}{16} & + \frac{2}{32} & + \cdots .Теперь обратите внимание, что, за исключением первого члена, мы получаем ГП с начальным членом \( \frac{2}{4} \) и знаменателем \( \frac{1}{2} \). Как оказалось, первый член часто не вписывался в шаблон последовательности, и нам просто повезло раньше. Таким образом, мы получаем
\[ \frac{1}{2} T = \frac{1}{2} + \frac{ \frac{2}{4} } { 1 — \frac{1}{2} } = \frac{ 1}{2} + 1 = \frac{3}{2} . \]
Следовательно, \( T = 3 ,\), откуда следует \( S = 2T = 6. \ _\квадрат \)
92\). Мы будем использовать другой подход, чтобы свести это к «линейно-геометрической прогрессии», которая является AGP.
\\
\конец{массив} \]Заметьте, что если мы возьмем разность членов квадратичной последовательности, мы получим линейную последовательность. Это справедливо и в более общем смысле: если мы возьмем разность терминов в последовательности степени \(n\), мы получим последовательность степени \(n-1 \). Это подробно рассмотрено в разделе «Метод различий». Мы будем неоднократно использовать эту идею для работы с такой «полиномиально-геометрической прогрессией».
9я } \).9n} + \cdots \]Обратите внимание, что у нас есть «кубическая геометрическая прогрессия» со знаменателем \( \frac{1}{3} \). Умножим на \( \frac{1}{3} \) и возьмем разницу:
\[ \begin{array} { r lllll}
S & = \frac{1}{3} & + \frac{8}{9} & + \frac{ 27}{27} & + \frac{ 64 }{ 81} & + \frac{ 125}{243} & + \cdots \\ \frac{1}{3} S & = & + \frac{1}{9} & + \frac{8}{27} & + \frac{ 27}{81} & + \frac{ 64}{ 243 } & + \cdots \\ \hline \frac{2}{3} S & = \frac{1}{3} & + \frac{7}{9{i+1} } \), что является «квадратично-геометрической прогрессией». Установите это как \(T\). Затем умножение на \( \frac{1}{3} \) и получение разницы дает\[ \begin{array} { r lllll}
T & = \frac{7}{9} & + \frac{ 19}{27} & + \frac{ 37}{ 81} & + \frac{ 61 }{243} & + \cdots\\ \frac{1}{3} T & = & + \frac{7}{27} & + \frac{ 19}{81} & + \frac{ 37}{ 243} & + \cdots \\ \hline \frac{2}{3} T & = \frac{7}{9} & + \frac{12}{27} & + \frac{ 18}{81} & + \frac{24}{243} & + \cdots. \\ \конец{массив} \] 9{i+2}} \), что является «линейно-геометрической прогрессией.\[ \begin{array} { r lllll}
U & = \frac{12}{27} & + \frac{ 18}{81} & + \frac{24}{243} & + \cdots \\
\frac{1}{3} U & = & + \frac{12}{81} & + \frac{ 18}{342} & + + \cdots \\
\hline
\frac{2}{3 } U & = \frac{12}{27} & + \frac{6}{81} & + \frac{6}{243} & + \cdots. \\ \конец{массив} \] 9{i+3} } ,\), которая представляет собой геометрическую прогрессию с бесконечной суммой \( \frac{ \frac{6}{81} } { 1 — \frac{1}{3} } = \frac{1 {9} \).Это дает нам
\[\begin{выравнивание} \frac{2}{3} U &= \frac{12}{27} + \frac{1}{9} &&\Стрелка вправо U = \frac{5}{6} \\ \frac{2}{3} T &= \frac{7}{9} + \frac{5}{6} &&\Rightarrow T = \frac{29}{12} \\ \frac{2}{3} S &= \frac{1}{3} + \frac{29}{12} &&\Стрелка вправо S = \frac{33}{8}. \ _\квадрат \конец{выравнивание}\]
Установите это как \( U \). Затем умножение на \( \frac{1}{3} \) и получение разницы дает Учитывая, что бесконечная сумма \( S\) может быть выражена как \( \frac ab\), где \(a\) и \(b\) взаимно простые натуральные числа, найти \ (а+б\).
Чтобы улучшить свои навыки решения задач по арифметическим прогрессиям, геометрическим прогрессиям и арифметико-геометрическим прогрессиям, вы можете посетить следующие вики:
- Арифметические и геометрические прогрессии: решение задач
Процитировать как: Арифметико-геометрическая прогрессия. Brilliant.org . Извлекаются из https://brilliant.org/wiki/arithmetic-geometric-progression/
Формулы геометрической прогрессии, геометрические ряды, бесконечные геометрические ряды
В математике геометрическая прогрессия (последовательность) (также неточно известная как геометрическая прогрессия ) представляет собой последовательность
таких чисел, что частное любых двух последовательных членов последовательности есть константа, называемая
обыкновенное отношение последовательности.
94…$
, где r ≠ 0, r — обыкновенное отношение, а a — масштабный коэффициент (также первый член).
Примеры
Геометрическая прогрессия с знаменателем 2 и масштабным коэффициентом 1 равна
1, 2, 4, 8, 16, 32…
Геометрическая последовательность с знаменателем 3 и масштабным коэффициентом 4 равна
4, 12, 36, 108, 324…
Геометрическая прогрессия с обыкновенным отношением -1 и масштабным коэффициентом 5 равна
5, -5, 5, -5, 5, -5,…
Формулы
Формула для n-го члена может быть определена как: 9{n-1}$
Формула обыкновенного отношения:
$r = \frac{a_k}{a_{k-1}}$
Если общее отношение:
- Отрицательный, результаты будут чередоваться между положительными и отрицательными .
Пример:
1, -2, 4, -8, 16, -32… — знаменатель равен -2, а первый член равен 1. - Больше 1, будет экспоненциальный рост до бесконечности (положительный) .
Пример :
1, 5, 25, 125, 625 … — обыкновенное отношение равно 5. - Меньше -1, будет экспоненциальный рост до бесконечности (положительный и отрицательный) .
Пример :
1, -5, 25, -125, 625, -3125, 15625, -78125, 390625, -1953125 … — обыкновенное отношение равно -5. - Между 1 и -1, будет экспоненциальное затухание к нулю .
Пример :
4, 2, 1, 0,5, 0,25, 0,125, 0,0625 … — обыкновенное отношение $\frac{1}{2}$
4, -2, 1, -0,5, 0,25, -0,125, 0,0625 … — обыкновенный коэффициент $-\frac{1}{2}$. 93 + \cdots = a\frac{1}{1-r}$, который действителен только тогда, когда |r| < 1.
a 1 — первое слагаемое.Калькулятор геометрической прогрессии
Задачи на геометрическую прогрессию
Задача 1.
Является ли последовательность 2, 4, 6, 8… геометрической прогрессией?
Решение: Нет, это не так. (2, 4, 8 — геометрическая прогрессия)Задача 2
Если 2, 4, 8.
