Геометрия круг: Окружность, круг, шар / Геометрия / Справочник по математике 5-9 класс

«Выдумщики» Форма для мыла №21 пластик Геометрия — КРУГ

Посуда

• Столовая посуда
• Столовые приборы
• Посуда для напитков
• Посуда для приготовления
• Кухонные принадлежности
• Украшения кулинарных изделий
• Упаковка для выпечки
• Формы
• Карвинг
• Термопосуда
• Ланч-боксы
• Емкости для хранения
• Техника для кухни

Продукты питания

• Декор кондитерский
• Добавки пищевые
• Смеси для выпечки
• Смеси для десертов
• Сладости
• Все категории >

Домашний текстиль

• Текстиль для кухни
• Текстиль для ванной
• Постельные принадлежности

Хозяйственные товары

• Уход за одеждой
• Уход за домом
• Инструменты для дома
• Наборы для ванной комнаты
• Все категории >

Хранение вещей

• Ключницы
• Корзины
• Коробки
• Крючки
• Все категории >

Декор интерьера

• Аромасвечи
• Интерьерные игрушки
• Интерьерные наклейки
• Копилки
• Подсвечники
• Постеры
• Предметы декора
• Рамки
• Светильники
• Свечи
• Снежные шары
• Статуэтки и фигурки
• Часы

Товары для сада

• Семена
• Инструменты для сада

Товары для рыбалки

Товары для праздников

Аксессуары для праздника

• Бенгальские свечи
• Гудки
• Микрофоны
• Мыльные пузыри
• Открытки
• Хлопушки

Подарочная упаковка

• Банты
• Бумага
• Конверты
• Коробки
• Ленты
• Мешки
• Наполнитель
• Пакеты

Фототовары

• Фотоальбомы
• Фотоаппараты
• Фотобутафория
• Фоторамки
• Все категории >

Украшения для праздника

• Бумажные фонарики
• Венки
• Воздушные шары
• Гирлянды
• Декоративные елочки
• Елочные игрушки
• Искусственный снег
• Конфетти
• Мишура и дождик
• Наборы для праздника
• Все категории >

Карнавальные товары

• Бороды
• Головные уборы
• Грим и временные тату
• Костюмы
• Маски
• Очки
• Парики
• Аксессуары

Тематические подборки

• 8 марта
• Свадебные аксессуары
• Товары для школы

Сувенирная продукция

• Амулеты и обереги
• Брелоки
• Визитницы
• Значки
• Магниты
• Награды
• Обложки для документов
• Подарки с приколами

Книги

Книги по рукоделию и творчеству

• Бисероплетение
• Валяние (фелтинг)
• Вышивание
• Вязание
• Декоративно-прикладное искусство
• Дизайн дома
• Изготовление кукол и игрушек
• Изготовление украшений
• Лепка
• Макраме и плетение
• Оригами, работа с бумагой
• Рисование и роспись
• Шитье
• Изготовление мыла и свечей

Детская литература

• Атласы
• Книги по рисованию
• Книги по творчеству
• Книги с играми
• Книги с наклейками
• Книги-аппликации
• Пособия и учебники
• Прописи
• Раскраски
• Заготовки
• Все категории >

Художественная литература

Книги-квесты

Антистресс-раскраски

Саморазвитие

Журналы

Карты настенные

Книги по кулинарии

Календари

Закладки для книг

Эзотерика

Подарочные сертификаты

* цвет на фото может незначительно отличаться

• Описание
• Характеристики
• Наличие в магазинах
• Отзывы (114)

Использовать пластиковые формы для мыла очень просто.

Растопите в стаканчике необходимое количество мыльной основы на водяной бане или в микроволновой печи средний вес, необходимый для данной формы, добавьте в нее краситель и отдушку, по желанию, хорошо перемешайте и вылейте смесь в форму. После полного застывания аккуратно извлеките готовое мыло из формы.

Если форма имеет сложный рисунок, то возможно небольшое затруднение при вынимании из нее готового мыла. Для этого, поместите на несколько минут форму вместе с застывшим кусочком мыла в морозилку. После этого ополосните форму горячей водой можно под краном и мыло легко выпадет из формы само. пластиковая форма на жестком каркасе для изготовления мыла в форме шайбы; размер готового мыла: d 65 мм, h 20 мм

Комментарий снабжения по шк:

размер товара не позволяет выводить большим размером ш/к, поставщику сообщено об данной проблеме

Марка:

«Выдумщики»

Материал:

пластик

Назначение:

для мыловарения

Объем единицы продажи, л:

1

Проблемный штрихкод:

Нечитаемый штрихкод

Страна происхождения:

Россия

Тип товара:

Форма

Вес готового изделия, г:

75

Размер готового изделия, мм:

65х20

Тематика:

Геометрия

Геометрия: свойства окружности и круга

Опубликовано 22.

11.202222.11.2022 от Admin — Оставить комментарий

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Круг — геометрическая фигура, состоящая из всех точек плоскости, расстояние от которых до точки O не превосходит R.

Определения для окружности и круга

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 

• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку. Общая точка прямой и окружности называется точкой касания. В этом случае d=R.
• Секущая — прямая, которая пересекает окружность в двух различных точках. В этом случае d<R.

• Круговой сектор —  пересечение круга с плоским углом, вершина которого находится в центре этого круга.
• Дуга окружности — геометрическая фигура, состоящая из всех точек окружности, принадлежащих некоторому плоскому углу с вершиной в центре этой окружности. Каждому такому углу соответствует ровно одна дуга окружности, и каждой дуге окружности соответствует ровно один плоский угол с вершиной в центре окружности.

Круговой сегмент — пересечение круга с полуплоскостью, расстояние от границы которой до центра круга меньше радиуса этого круга. Если граница полуплоскости содержит центр круга, то соответствующий круговой сегмент называется полукругом.

Свойство хорды окружности

Произведения отрезков пересекающихся хорд равны между собой, т. е. ab = cd.
На рисунке: CA⋅CA1=CB⋅CB1=R2−d2

Свойства касательной окружности

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

Свойства двух касательных из одной точки к окружности:
Пусть из точки A к окружности проведены две касательные AB1 и AB2 и O – центр окружности. Тогда:
1. AB1=AB2;
2. AO – биссектриса угла B1AB2;
3. OA – биссектриса угла B1OB2.

Свойство секущих к окружности

• Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков секущей, соединяющих данную точку и точки ее пересечения с окружностью, т.е. a2 = bc. ИЛИ Квадрат касательной равен произведению секущей на ее внешнюю часть. На рисунке:
  CD²=d²−R²
  CD²=CA⋅CA₁=CB⋅CB₁
• Если из точки, взятой вне окружности, к окружности проведено несколько секущих, то произведения больших отрезков секущих на их внешние части равны между собой. На рисунке: CA⋅CA₁=CB⋅CB₁

 

Основные формулы для окружности и круга:

Длина окружности: Площадь круга: или
где:
π= 3,14 (3,1415926535) – величина постоянная,
r-радиус,
d –диаметр,
L – длина окружности,
S-площадь.

 

Площадь кругового сектора

Площадь кругового сектора равна: где α – радианная мера центрального угла, отвечающего данному сектору, R – радиус круга.

Площадь сегмента

Площадь кругового сегмента равна: где α – радианная мера центрального угла, отвечающего данному сегменту, R – радиус круга.

 

Калькулятор для окружности и круга поможет вычислить все характеристики круга по одной из известных величин.

 

Рубрика: Для школьников

Метки Математика, Геометрия

Circles [300-страничный бесплатный курс GMAT][2023]

300-страничный бесплатный курс GMAT

Бесплатный курс GMAT > GMAT Math Basics > 3. Geometry > Circles

Circles

A  4 90 is 1 90 is 1 90 is 1 90 множество всех точек плоскости, находящихся на одинаковом расстоянии от центра . Круг имеет 360°.

Видео предоставлено Kaplan Подготовка к GMAT .

Отрезок от центра круга до круга называется радиус   r .

Отрезок, проходящий через окружность через центр, называется  диаметром   d .

Диаметр круга в два раза больше радиуса.

Длина окружности — это расстояние по окружности.
Формула длины окружности:  C  = 2 πr  =  πd .

Формула площади круга:  A  =  πr ² .

При использовании формулы площади убедитесь, что используемое значение является радиусом, а не диаметром. Это случайная ловушка GMAT.

При использовании оценки значения π  ( pi ) попробуйте  π  ≈ 3. Если вам нужна более точная оценка, используйте: }

Помните, что GMAT требует рассуждений, а не долгих вычислений. Оставьте π в своих вычислениях. Используйте оценку только для 9 0012 π , если варианты ответов содержат числа вместо π .

Если у вас есть радиус, диаметр, длина окружности или площадь круга, вы можете найти все остальные значения.

Чему равен радиус круга, если его длина окружности численно равна удвоенной площади?

Решение

Используйте формулы, чтобы написать уравнение с длиной окружности, равной 2 (площадь), затем найдите  r .

C  = 2 πr               A  =  πr ²

2 πr  = 2( πr ² ), so  r  = 1.

An automobile travels 2 мили. Сколько оборотов делает шина с радиусом 14 дюймов?

Решение

Количество оборотов равно расстоянию, деленному на длину окружности шины. Поскольку есть деление, сохраняйте числа в факторизованной форме, а не вычисляйте полностью.

Окружность шины с 
r  = 14 составляет 28 π дюймов.

Одна миля = 5 280 футов = 12 (5 280) дюймов. Две мили = 24 (5280) дюймов.

\dfrac{24 × 5,280}{28π} = \dfrac{24 × 5,280}{\dfrac{28 × 22}{7}}            … Замените \dfrac{22}{7} на   π .

= \dfrac{24 × 5,280 × 7}{28 × 22}            … Умножьте на обратную величину знаменателя.

= \dfrac{5280 × 6 × 7}{7 × 22} = \dfrac{5280 × 3}{11}            … Фактор и отмена.

Хитрость заключается в том, что вы можете разлагать дальше, потому что 5280 делится на 11.

\dfrac{5,280 × 3}{11} = 480 ×  3   =  1 140

Колесо совершит 1 140 оборотов.

Решение

За 6 часов точка M  на минутной стрелке проходит 6 окружностей радиусом = 3 r .
Итак, точка M проходит 6 × 2 π 3 r  = 36 πr .

Точка  H  на часовой стрелке проходит только половину оборота, половину окружности, с радиусом =  р .
Итак, точка H  проходит (\dfrac{1}{2}) ×  2 πr  =  πr .

Таким образом, отношение равно 36 πr : πr или 36 : 1.

Правильный вариант ответа — (E).

Центральные углы

[[https://youtu.be/0-uEVVBe1ZA]]

Центральный угол имеет вершину в центре окружности, поэтому он образован двумя радиусами.
дуга является частью круга.

Мера центрального угла равна длине дуги, на которую он опирается.

По кругу  O , центральный угол ∠ AOB  = 60°. Дуга AB равна 60°.

Сектор  – это «кусок пирога», образованный центральным углом и его дугой. Сектор имеет периметр и площадь.

У некоторых часов минутная стрелка ровно в 3 раза длиннее часовой. Точка M  находится на кончике минутной стрелки, а точка  H  находится на кончике часовой стрелки. Каково отношение расстояния, которое проходит точка M , к расстоянию, которое проходит точка H за 6 часов?

(a) 3: 1 (b) 6: 1
(c) 12: 1 (d) 18: 1
(e) 36: 1

и BD  – это диаметры. Найдите меры всех углов и дуг.

Решение

Используя вертикальные углы, ∠2 = 130°.
AC  это линия, поэтому ∠1 + ∠2 = 180° и ∠1 = 50°.
Аналогично, ∠3 = 50°.

Дуги имеют ту же меру, что и их центральные углы, поэтому
дуги н.э.  = дуге до н.э.  = 50°.

Дуга AB = дуга CD  = 130°.

Площадь заштрихованной области 24 π . Найдите меру дуги ABC .

Решение

Отношение площади сектора к площади всего круга равно отношению мер дуги.

Площадь всего круга равна  A  =  πr ²  = 36 π . Площадь сектора 24 π .

Установите пропорцию.

\dfrac{сектор}{круг} = \dfrac{24π}{36π} = \dfrac{\textit{x}}{360}
\\[3ex]\dfrac{2}{3} = \dfrac{ \textit{x}}{360}  так  x = 240°. Мера дуги ABC = 240°.

Найдите периметр и площадь сектора 36° круга с радиусом 10.

Решение

Сектор 36° равен } круга.
Периметр сектора будет равен радиусу + радиусу
+ (\dfrac{1}{10}) окружности окружности.
Длина окружности равна  C  = 2 πr = 20 π .
P  = 10 + 10 + (\dfrac{1}{10})20 π   = 20 + 2 π

Площадь сектора будет равна \dfrac{1}{10} площади круга.
Площадь круга равна 
A  =  πr ²  = 100 π .

a = (\ dfrac {1} {10}) 100 π = 10 π

вставленные углы

. Вставка в надписи имеет его вертеро. два аккорда.

Мера вписанного угла равна \dfrac{1}{2} мере дуги, на которую он опирается.

По кругу O , ∠ RTS = 50°. Мера дуги RS составляет 100°.

Если две хорды конгруэнтны, то дуги, образованные хордами, конгруэнтны.
Это верно, если хорды являются частью вписанного угла или просто окружности.

В круг О , ТУ = ТУ и дуга ТУ = дуга ТУ .

В кругу O выше, ∠ STU = 30°. Каковы размеры дуги СУ , дуги ТУ и дуги ТУ ?

Решение

Вписанный угол ∠ STU  = 30°, поэтому дуга SU  = 60°.

Окружность равна 360°, поэтому
дуга RS + дуга SU + дуга TR + дуга TU  
= 360°.
Используйте x для меры
дуга ТР = дуга ТУ .
100 +60 + x + x = 360
2 x = 200

x = 100 ARC TR = ARC TU = 100 °

11111. ДЛЯ ДЕЛЕ вписанный угол 42° в окружность с r = 12 метров?

Решение

Вписанный угол 42° равен \dfrac{1}{2} дуги, поэтому дуга равна 84°.

Дуга является частью всей окружности, поэтому 84° является частью 360°. Найдите дробь.

\dfrac{84}{360} = \dfrac{7 × 12}{3 × 10 × 12} = \dfrac{7}{30}\\[3ex]

Длина окружности равна 2 πr = 24 π .

Итак, длина дуги равна (\dfrac{7}{30})(24 π ).

Поскольку это дробь, в числителе которой стоит 7, используйте π = \dfrac{22}{7}. Не забывайте множить, а не умножать, чтобы избежать вычислений.

(\dfrac{7}{30})(24π) ≈ (\dfrac{7}{30})(24)(\dfrac{22}{7})

= \dfrac{7 × 4 × 6 × 22}{5 × 6 × 7} = \dfrac{88}{5} = \dfrac{176}{10} = 17,6

Длина дуги составляет около 17,6 метра.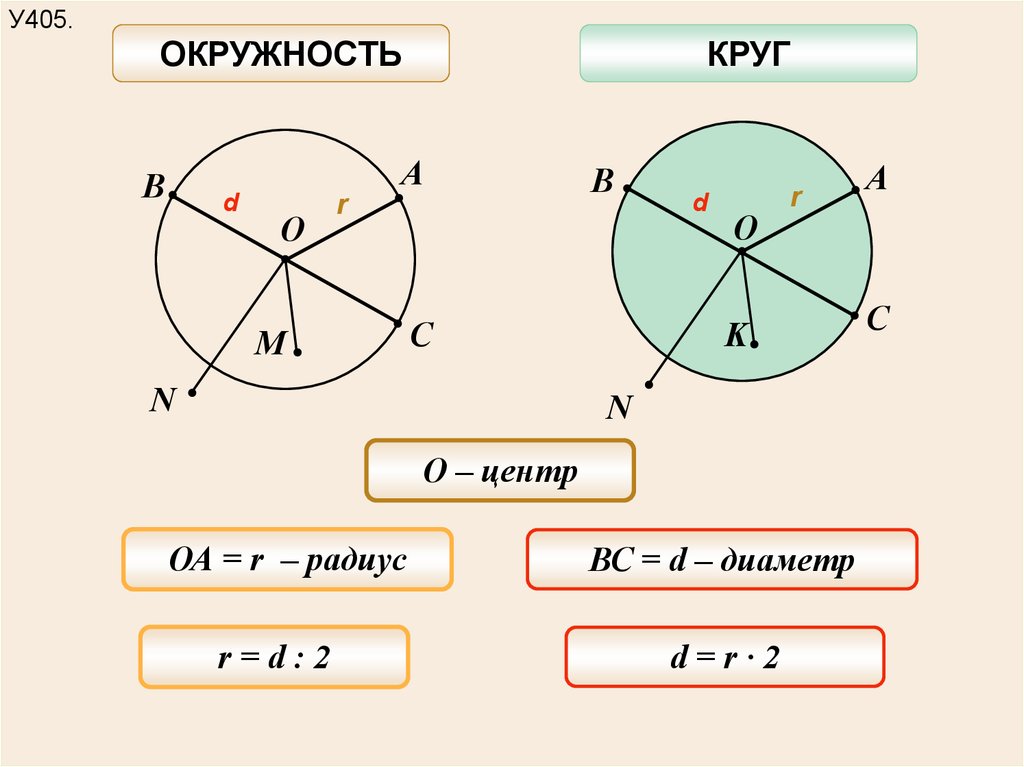

Найдите площадь заштрихованной области.

Решение

Вписанный угол равен 45°, поэтому дуга равна 90°.
90° говорит вам искать прямоугольный треугольник.
Радиус рисования OC  составляет прямоугольный треугольник AOC . Заштрихованная область — это сектор минус треугольник.

Треугольник  AOC  является равнобедренным прямоугольным треугольником, поэтому основание = высота = 4.  Площадь равна (\dfrac{1}{2})(4)(4) = 8.

Центральный угол сектора равен 90°, поэтому его площадь равна \dfrac{90}{360} = \dfrac{1}{4} площади круга.
Площадь сектора равна
(\dfrac{1}{4})( π )(4 ² ) = 4 π .

Площадь заштрихованной области 4 π   – 8.

Если вам нужно рассчитать оценку, сначала умножьте.
4 π   – 8  = 4 ( π   – 2). Используйте 3,14 в качестве оценки для  π .
4 ( π — 2) ≈ 4 (3,14 — 2) = 4 (1,14) = 4,56

. круг.

В GMAT часто используются вписанные многоугольники. Вам нужно уметь комбинировать информацию об окружностях, углах и многоугольниках.

Существует два важных соотношения между углами вписанных многоугольников.

• Если одна сторона вписанного треугольника равна диаметру, то треугольник прямоугольный.

Это легко увидеть. Мера вписанного угла равна \dfrac{1}{2} дуги, на которую он опирается. Диаметр делит окружность на две дуги по 180°. Значит, вписанный угол в дугу равен 90°.

• Противолежащие углы вписанного четырехугольника в сумме дают 180°.

Вспомните также, что сумма внутренних углов четырехугольника равна 360°.

Треугольник со сторонами 6 и 8 единиц вписан в окружность. Если третья сторона является диаметром, найдите длину этого диаметра.

Решение

Треугольник с одной стороной диаметром является прямоугольным.

Длины сторон этого треугольника равны 6 : 8 :  ч . Это кратное
прямоугольного треугольника 3 : 4 : 5, поэтому длина гипотенузы, являющейся диаметром, равна 10,9.0003

Найдите значения x , y и z .

Решение

Окружность — это сумма дуг, поэтому начните с нахождения 3 z °.
360° = 110° + 130° + 54° + 3 z °  так что 3 z ° = 66° и  z  = 22.

Два других угла можно найти двумя способами.

Метод 1
Меры вписанных углов равны половине суммы противолежащих дуг.

Используя противоположные дуги:
2 x ° = (\dfrac{1}{2})(66° + 110°) 
, поэтому 2x° = (\dfrac{1}{2})176° и x  = 44,
6 y ° = (\dfrac{1}{2})(66° + 54°) 
, поэтому 6y° = 60° и  y  = 10,

Метод 3
Поскольку вписанный многоугольник является четырехугольником, сумма противоположных углов четырехугольника составляет 180°.

Мера вписанного
∠ C  =  (\dfrac{1}{2})(130° + 54°) = 92°.
Добавьте противоположные углы.
2 x ° + 92° = 180°, поэтому 2 x ° = 88° и  x  = 44.

Мера вписанного
∠ B  1 {2}dfrac) (130° + 110°) = 120°.
6 y ° + 120° = 180°  
поэтому 6 y ° = 60° и y  = 10.

Квадрат вписан в отношение площади, равной 20. круга к площади квадрата.

Решение

Нарисуйте фигуру.

Вам нужно найти площадь круга и квадрата.

Будьте осторожны! Поскольку диаметр = 20,
r = 10, а площадь круга A = πr ² = 100 π .

Обратите внимание, что диаметр делит квадрат на два прямоугольных треугольника 45° : 45° : 90°. Гипотенуза – это диаметр, поэтому число равно 20. Каждая сторона квадрата равна

\dfrac{20}{\sqrt{2}} = \dfrac{20}{\sqrt{2}} \times \dfrac{\sqrt{ 2}}{\sqrt{2}} = 10\sqrt{2}            
Площадь квадрата равна (10\sqrt{2}) ²  
= 100  ×  2 = 200.

Отношение площадей равно \dfrac{100\textit{π}}{200 } = \dfrac{\textit{π}}{2}

Касательные к окружности

Касательная к окружности — это прямая, которая касается окружности только в одной точке.

Касательная перпендикулярна диаметру.

Углы, образованные хордой и касательной, являются \dfrac{1}{2} мерой дуги.

Касательные из общей внешней точки конгруэнтны. Мерой угла, образованного касательными, является \dfrac{1}{2} разность между мерами двух дуг.

В треугольнике ABC найдите длину каждой дуги вписанной окружности.

Решение

Начните с прямого угла, ∠ A . Пусть мера дуги RST = x и мера дуги RT  = y .

x  +  y = 360            …Сумма дуг – это полный круг.

\dfrac{1}{2}( x  –  y ) = 90            … Мерой угла является \dfrac{1}{2} разность дуг.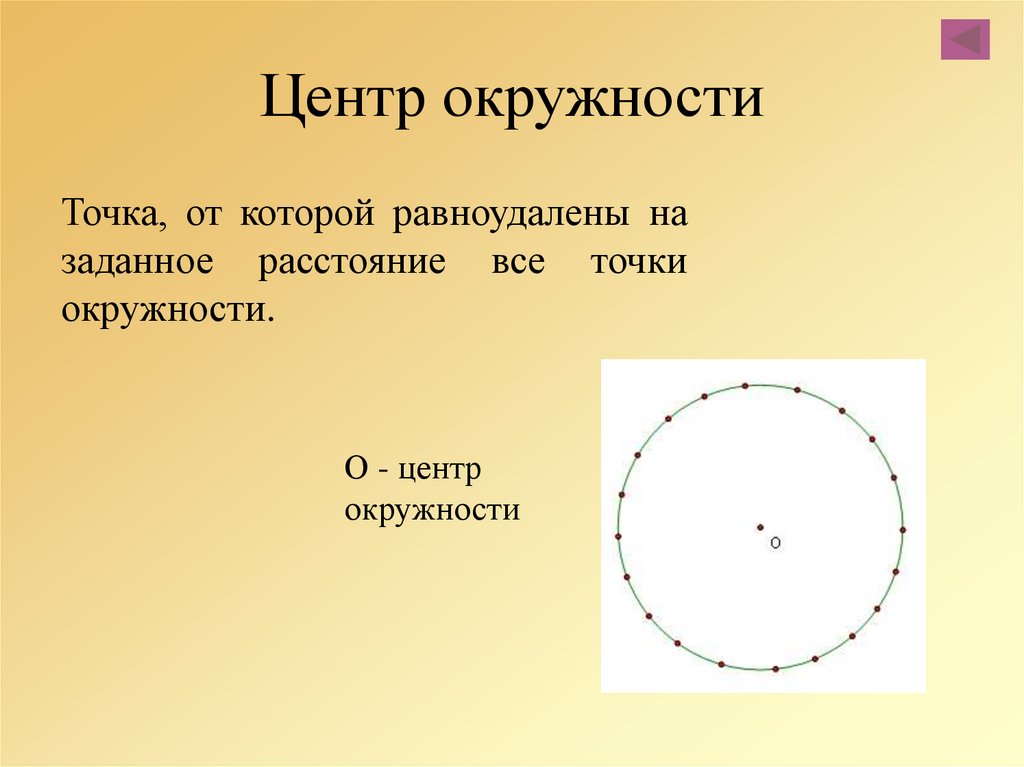

x  –  y = 180            … Упростите.

Решите систему уравнений.

x  +  y = 360
x  –  y = 180
2 x = 540 SO x = 270.

x + y = 360 SO y = 360 — 270 = 90. ARC RT = 90 °

. Другие уголки B и 90 °

. C оба являются углами по 45°, поэтому дуга RS = дуга ST .
Пусть мера
дуги  RS  = дуга  ST  =  z .

дуга RS + дуга ST + дуга RT  = 360°
Z + Z + 90 = 360
2 Z = 270 SO Z = 135.
ARC RS = ARC ST = 135 °

в Крунге, пример выше, примере радиус вписанной окружности равен 10. Найдите площадь треугольника ABC .

Решение

Сделайте набросок.

Чтобы найти площадь, нужна длина любой стороны или длина отрезка AS как высота треугольника АВС .

Поскольку диаметр перпендикулярен касательной, радиусы OS , OR и OT перпендикулярны сторонам треугольника ABC .

Радиусы OR и OT образуют квадрат AROT  со стороной 10. Диагональ квадрата образует прямоугольные треугольники 45° : 45° : 90°, поэтому длина диагонали равна
10\sqrt {2}.
Таким образом, длина сегмента AS равна
10 + 10\sqrt{2}.

Отрезок AS является высотой треугольника ABC , но длина основания BC неизвестна.

Отрезок AS также образует два прямоугольных треугольника
45° : 45° : 90° в треугольнике ABC , треугольнике ASB и треугольнике ASC . Таким образом, сегменты AS , SB и SC равны.
Итак, высота AS = 10 + 10\sqrt{2} и основание BC = 2(10 + 10\sqrt{2}).

Площадь треугольника ABC
= \dfrac{1}{2}[2(10 + 10\sqrt{2})](10 + 10\sqrt{2} )
= (10 + 10\sqrt{ 2}) ²
= [10(1 + \sqrt{2})] ²             …Множитель перед умножением.
= 102 (1 + \ sqrt {2}) ² … Правило экспонента ( AB ) ² = A ² B ²
= 100 (1 + 2 } + 2)
= 100(3 + 2\sqrt{2})

Если варианты ответа не включают \sqrt{2}, используйте 1,4 в качестве приблизительного значения.
100(3 + 2\sqrt{2}) ≈ 100[3 + 2(1.4)]
= 100(5.8) = 580

Видеовикторина

Круги

Лучше смотреть в ландшафтном режиме

4 вопроса с видео объяснения

100 секунд на вопрос

Перейти к вопросу ( 1 )

Время истекло

Повтор видео

Повтор видео

Выберите правильный ответ.

А

В

С

Г

Е

Нажмите ВЫБОР, чтобы начать видео.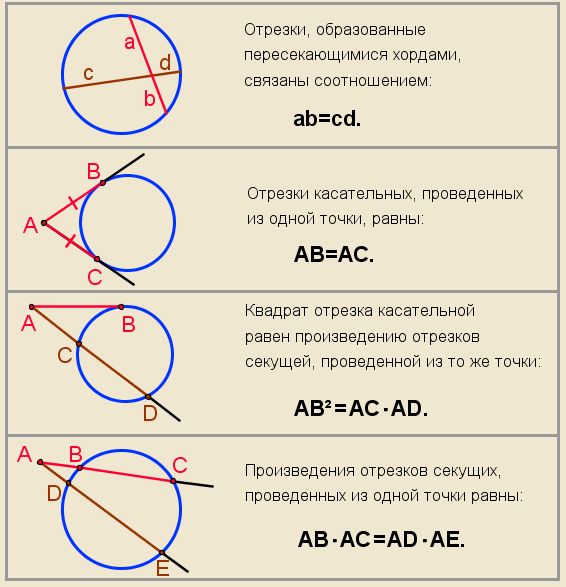

Не забудьте включить громкость, чтобы услышать объяснение.

https://www.youtube.com/watch?v=SwFbfB64Gs0
https://www.youtube.com/watch?v=fxAie4PCNZQ
https://www.youtube.com/watch?v=W1edsOVAmqw

Прежде чем пытаться решить эти проблемы, обязательно просмотрите этот раздел, посвященный вопросам достаточности данных.

https://www.youtube.com/watch?v=tYlf4JYJ908
https://www.youtube.com/watch?v=6fGAkVfMXEU
https://www.youtube.com/watch?v=Nerw -crkj80
https://www.youtube.com/watch?v=HPD1jQEFhJU

Найдите местные классы и расписание GMAT, используя нашу базу данных более чем 150 городов.

Найти курсы GMAT

SOLIDS →

Гиперболическая геометрия — окружности | Математическая ассоциация Америки

Вы находитесь здесь

Главная » Публикации MAA » Периодические издания » Loci/JOMA » Гиперболическая геометрия — окружности

‹ Гиперболическая геометрия — треугольники, углы и площади вверх

Автор(ов):

Эндрю Г.

Беннетт

 

Окружность на гиперболической плоскости — это геометрическое место всех точек, находящихся на фиксированном расстоянии от центра, как и на евклидовой плоскости. Следовательно, гиперболическая плоскость по-прежнему удовлетворяет третьей аксиоме Евклида. Гиперболический круг оказывается евклидовым кругом после того, как он сплющивается в модели полуплоскости Пуанкаре. Единственное отличие состоит в том, что, поскольку расстояния ближе к краю больше, центр гиперболического круга не совпадает с евклидовым центром, а смещен к краю полуплоскости.

Теперь, когда мы знаем, как находить линейные расстояния и площади треугольников, мы можем найти длину окружности и площадь круга, используя тот же прием, что и Архимед, аппроксимируя круг вписанными и описанными n -угольниками и найдя пределы. Как отмечалось на предыдущей странице, в гиперболической геометрии нет понятия подобия, поэтому неудивительно, что формулы для гиперболической окружности и площади не являются простыми пропорциями, как в евклидовом случае.

В гиперболической геометрии

• Окружность = 2 pi sinh r
• Площадь = 4 pi sinh ² ( r /2)

где r — радиус окружности.

Апплет

Чтобы помочь вам познакомиться с гиперболическими кругами, я подготовил апплет, который позволит вам поэкспериментировать с ними. Для запуска апплета вам потребуется браузер с поддержкой Java (Netscape 3.0 или более поздней версии или Internet Explorer 3.0 или более поздней версии в Windows 95 или Mac). Прочитав следующие инструкции, щелкните ссылку ниже, чтобы запустить апплет в новом окне. Если разрешение вашего монитора 640×480, вы, вероятно, захотите развернуть окно. Если разрешение вашего монитора 800×600 или больше, вы должны видеть все так, как оно выглядит само по себе.

В апплете у вас будет красная точка в центре круга и синяя точка на круге. Точки соединены (гиперболическим) отрезком линии, радиус выделен красным, а сам (гиперболический) круг нарисован синим. Щелкните мышью точку и перетащите ее (удерживая кнопку мыши нажатой), чтобы переместить точку. Радиус и окружность будут следовать за точкой. За краем полуплоскости (отмечено серым) вы увидите гиперболическое расстояние между красной и синей точками. ( Предупреждение об ошибке: Иногда, когда окно закрывается, а затем открывается другими окнами на мониторе вашего компьютера, апплет не перерисовывается полностью. Если щелкнуть точку и переместить ее или свернуть, а затем восстановить окно, апплет перерисуется правильно.)

Что попробовать

• Как выглядит длина окружности гиперболического круга заданного радиуса сравнить с окружностью евклидова окружности того же радиуса? Имеет ли значение, сравниваете ли вы большие круги или маленькие круги?
• Чем отличается площадь гиперболического круга заданного радиуса от площади евклидова круга того же радиуса? Имеет ли значение, сравниваете ли вы большие круги или маленькие круги?
• Как быстро длина окружности и площадь увеличиваются по мере увеличения радиуса? Как это соотносится с евклидовым случаем?
• Обратите внимание, что длина окружности всегда превышает площадь гиперболического круга.

  No related posts.