Задачи категории В8. Параллелограмм, вычисление длин и углов
Задача 1. Сумма двух углов параллелограмма равна . Найдите один из оставшихся углов. Ответ дайте в градусах.
Решение: + показать
Задача 2. Один угол параллелограмма больше другого на . Найдите больший угол. Ответ дайте в градусах.
Решение: + показать
Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.
Решение: + показать
Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы и Найдите больший угол параллелограмма. Ответ дайте в градусах.
Решение: + показать
Задача 5. Периметр параллелограмма равен Меньшая сторона равна Найдите большую сторону параллелограмма.
Решение: + показать
Задача 6. Две стороны параллелограмма относятся как а периметр его равен Найдите большую сторону параллелограмма.
Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.
Решение: + показать
Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Решение: + показать
Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен
Решение: + показать
Задача 10. В параллелограмме высота, опущенная на сторону из точки равна . Найдите синус угла .
Решение: + показать
Задача 11. В параллелограмме Найдите высоту, опущенную на сторону
Решение: + показать
Задача 12.
Решение: + показать
Задача 13. Площадь параллелограмма равна две его стороны равны и Найдите большую высоту этого параллелограмма.
Решение: + показать
Задача 14. В параллелограмме . Найдите .
Решение: + показать
Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Решение: + показать
Задача 16. Площадь параллелограмма равна Точка — середина стороны . Найдите площадь трапеции .
Решение: + показать
Задача 17. Площадь параллелограмма равна Найдите площадь параллелограмма вершинами которого являются середины сторон данного параллелограмма.
Решение: + показать
Задача 18. Найдите диагональ параллелограмма , если стороны квадратных клеток равны 1.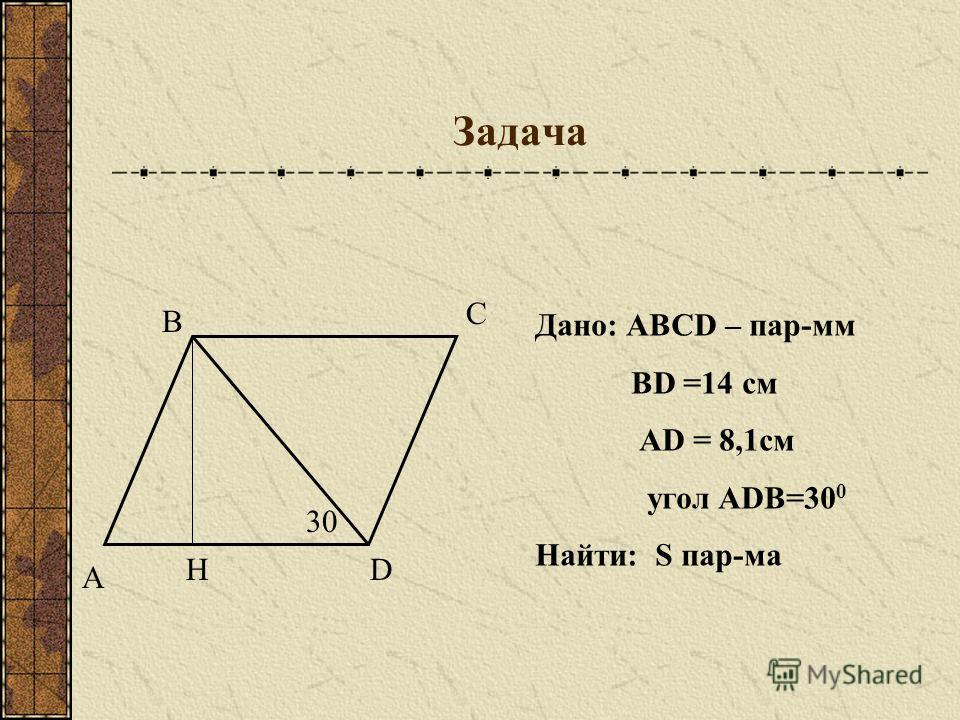
Решение: + показать
Задача 19. Диагонали четырехугольника равны и Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение: + показать
Вы можете пройти тест по теме «Параллелограмм. Вычисление углов и длин».
Какие задачи использует репетитор по математике на параллелограмм в 8 классе — Колпаков Александр Николаевич
Предлагаю Вашему вниманию страницы своей коллекции задач по геометрии для 8 класса. Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.
Задачи репетитора на параллелограмм и свойство угла в 30 градусов.
1) На стороне AB параллелограмма ABCD отмечена середина M. Найдите расстояние от M до AD, если и MC=10 см.
2) Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, .
Найдите расстояние от P до стороны AB. Задача на дом.
Задачи на биссектрисы углов:
Точка М середина стороны BC параллелограмма ABCD, причем AM и DM — биссектрисы углов BAD и ADC. Найдите DM, если и BC=6 см.
2) На стороне AD параллелограмма ABCD отмечена точка N так, что BN и CN — биссектрисы его углов B и C. Известно, что BN=4 и AD=8см. Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.
Репетитору по математике в копилку красивых задач на параллелограмм
На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.
Школьная математика (особенно геометрия) сильно ограничивает репетитора в варьировании простейшими объектами для составления с их участием комбинированных задач под конкретную учебную ситуацию. В начале 8 класса список пройденных теорем и понятий весьма невелик. Поэтому репетитор по математике всегда испытывает определенный недостаток в материале узкого назначения.
Простые задачи — однотипные, а сложных не так много. Первые не дают развития, а последние доступны далеко не всем учащимся. Найди что-то интересное посередине — отличительная черта хорошего репетитора по математике. Недавно летом я попал ситуацию, когда со средним учеником 8 класса были перерешены все виды типовых номеров учебника и дидактических материалов (я не беру задачи — клоны). Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.
Задача, которая была представлена выше явилась результатом таких поисков. Для того, чтобы получить правильную домашнюю задачу на параллелограмм и треугольники репетитору по математике достаточно симметрично отобразить эти треугольники относительно сторон BC и AD. Вы видите их на рисунке справа. Нужно доказать, что BPDK — параллелограмм.
Как репетитор по математике растягивает задачи?
Как правило, любую задачу можно «дожать» или «растянуть», оптимизируя ее под конкретные цели повторения тех или иных теорем и формул. Я ругулярно комплектую задачи по геометрии несколькими пунктами в графе «докажите». В каждый номер с равносторонними треугольниками репетитору по математике можно посоветовать включить еще один пункт: докажите, что
Вы можете изучить рабочий листочек (план на урок) с этими задачами, который я обычно готовлю каждому ученику. Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.
Надеюсь, что репетиторам по базовой математике 8 класса пригодятся предоставленные материалы для работы со средним и даже сильным учеником. Удачного плана на урок!
Репетитор по математике в Москве ( м. Строгино ). А.Н. Колпаков
Параллелограммы — Математика для старших классов
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Плоская геометрия » Четырехугольники » Параллелограммы
Ниже показан параллелограмм с размерами в см.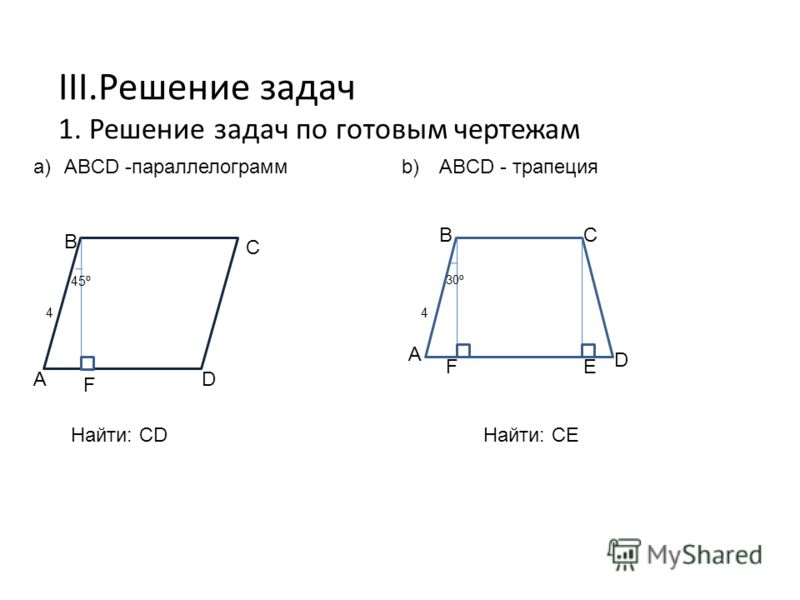
Чему равен периметр параллелограмма в см?
Возможные ответы:
Правильный ответ:
Объяснение:
Треугольник в левой части рисунка имеет угол a и . Поскольку сумма всех углов треугольника должна быть равна , мы можем найти угловую меру третьего угла:
Наш третий угол равен , и у нас есть треугольник.
Треугольник имеет стороны, которые находятся в соответствующем отношении . В этом случае сторона, противоположная нашему углу, равна , поэтому
Теперь мы также знаем, что
Теперь мы знаем длины всех недостающих сторон. Правая и левая стороны параллелограмма будут равны . Нижний и верхний будут каждый . Давайте объединим их, чтобы найти периметр:
Отчет о ошибке
Найдите периметр следующего параллелограммы:
Возможные ответы:
0016 Правильный ответ:
Объяснение:
Формула периметра трапеции:
,
, где – длина основания, а – длина ребра.
Противоположные стороны параллелограмма имеют одинаковую длину. Следовательно, оба ребра и оба основания равны.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:Формула для периметра параллелограмма:
где это длина большей стороны и это длина более короткой стороны.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите периметр следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Формула периметра параллелограмма:
.
Подставив наши значения, мы получим:
Сообщить об ошибке
ABCD — параллелограмм. BD = 5. Все углы треугольника ABD равны. Чему равен периметр параллелограмма?
Возможные ответы:
Правильный ответ:
Пояснение:
Если в треугольнике ABD все углы равны, а прямая BD делит параллелограмм, то и в треугольнике BDC должны быть равны все углы.
Теперь у нас есть два равносторонних треугольника, поэтому все стороны треугольников будут равны.
Следовательно, все стороны равны 5.
5+5+5+5 = 20
Сообщить об ошибке
Каково значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Противоположные углы равны, а сумма смежных углов должна равняться 180.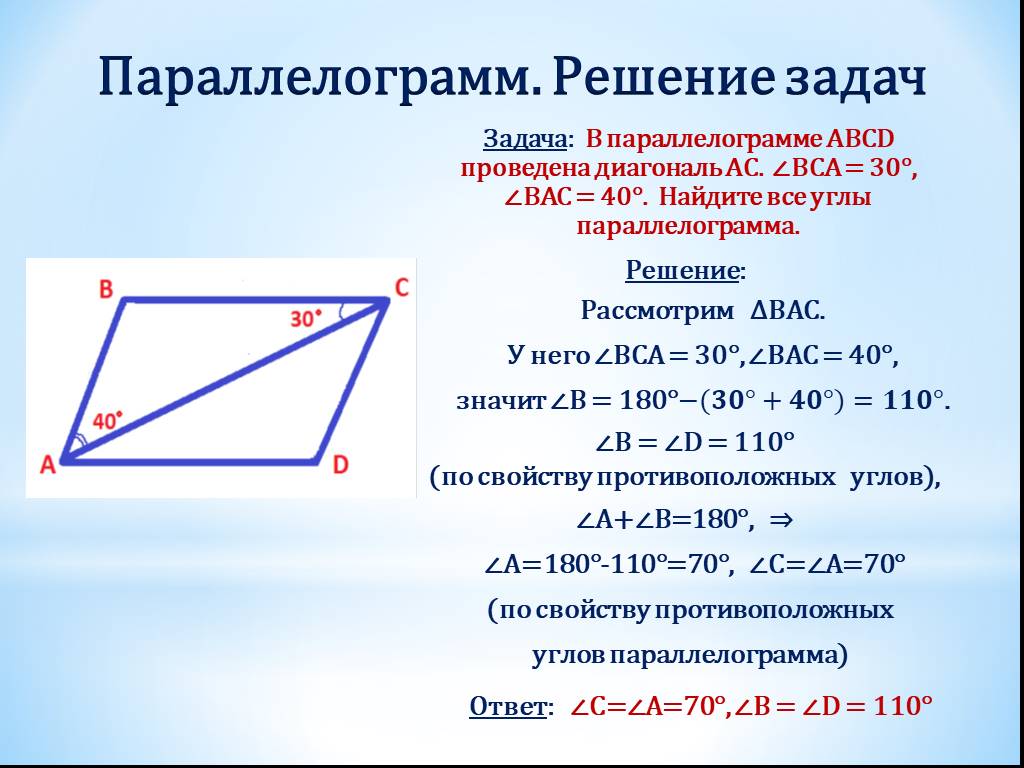
Следовательно, мы можем составить уравнение для решения z:
(z – 15) + 2z = 180
3z — 15 = 180
3z = 195
z = 65
Теперь найдите x:
2 z = x = 130°
Сообщить об ошибке
Какова площадь параллелограмма с основанием и высотой ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.
В этом уравнении длина основания и длина высоты. Мы можем указать длину стороны как для основания, так и для высоты, как указано в вопросе.
Сообщить об ошибке
Какова площадь параллелограмма с основанием и высотой ?
Правильный ответ:
Пояснение:
Чтобы решить этот вопрос, вы должны знать формулу площади параллелограмма.
Формула
Таким образом, мы можем подставить длину стороны как для основания, так и для высоты, чтобы получить
Выполните умножение, чтобы получить ответ .
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Возможные ответы:
Невозможно определить по данной информации.
Правильный ответ:
Объяснение:
Формула площади параллелограмма:
,
где — длина основания, а — длина высоты.
Чтобы найти высоту параллелограмма, воспользуйтесь формулой для треугольника:
, где – сторона, противоположная .
Левая сторона параллелограмма образует следующий треугольник:
, где длина высоты.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите площадь следующего параллелограмма:
Возможные ответы:
Правильный ответ:
Объяснение:
Используйте теорему Пифагоре, чтобы определить длину диагонали:
Площадь параллелограммы в два раза превышает площадь Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Плоская геометрия. Электронное обучение.
Параллелограмм, перпендикуляр, диагональ, метрические отношения.
