Гиперболический косинус — frwiki.wiki
Для одноименных статей см Косинус (значения) .
Гиперболический косинус, по математике, А гиперболическая функция .
Резюме
- 1 Определение
- 2 свойства
- 2.1 Общие свойства
- 2.2 Тригонометрические свойства
- 2.3 Расширение ряда Тейлора
- 2.4 Полиномы Чебышева
- 3 значения
- 4 нуля
- 5 Взаимная функция
- 6 Использование
- 6.1 Физика
- 6.2 Архитектура
- 7 Примечания и ссылки
- 8 См. Также
Определение
Гиперболический косинус функция, обозначается (или ), является следующей комплексной функцией : шиш{\ displaystyle \ cosh}ch{\ displaystyle \ operatorname {ch}}
- шиш:ПРОТИВ→ПРОТИВz↦еz+е-z2{\ displaystyle {\ begin {matrix} \ cosh: & \ mathbb {C} & \ to & \ mathbb {C} \\ & z & \ mapsto & \ displaystyle {\ frac {\ operatorname {e} ^ {z} + \ operatorname {e} ^ {- z}} {2}} \ end {matrix}}}
где — комплексная экспонента . {z}}
{z}}
Следовательно, функция гиперболического косинуса является четной частью комплексной экспоненты. Она ограничена на вещественной функции вещественной переменной .
Функция гиперболического косинуса, ограниченная, является в некотором смысле аналогом функции косинуса в гиперболической геометрии .
Обозначение Ch. X был введен Винченцо Риккати в XVIII — го века.
Характеристики
Общие свойства
- сп является непрерывной и даже голоморфна следовательно класса С ∞ ( т.е. бесконечно дифференцируема ). Его производной является функция гиперболического синуса, отмечает sinh .
- сЬ является пара .
- В примитивов из сЬ являются зп + С, где С является постоянная интегрирования.
- ch строго возрастает над ℝ + .
Тригонометрические свойства
Из определений функций гиперболического косинуса и синуса мы можем вывести следующие равенства, справедливые для любого комплекса и аналогичные формулам Эйлера в круговой тригонометрии: z{\ displaystyle z}
- еzзнак равношишz+грехzа такжее-zзнак равношишz-грехz,следовательношиш2z-грех2zзнак равно1.
 {2} +1} {2 \ mathrm {e}}}} ;
{2} +1} {2 \ mathrm {e}}}} ;- шишязнак равнопотому что1{\ Displaystyle \ сп \ mathrm {я} = \ соз 1}.
Нули
Все нули в ch — чистое воображение . Точнее, для любого комплексного числа , z{\ displaystyle z}
- шишzзнак равно0⇔z∈яπ(Z+12).{\ displaystyle \ cosh z = 0 \ Leftrightarrow z \ in \ mathrm {i} \ pi \ left (\ mathbb {Z} + {\ frac {1} {2}} \ right).}
Действительно, либо с реалом. Это было тогда, так zзнак равноИкс+яу{\ Displaystyle г = х + \ mathrm {я} у}Икс,у{\ displaystyle x, y}шишzзнак равношишИкспотому чтоу+ягрехИксгреху{\ Displaystyle \ сш г = \ сш Икс \ соз у + \ mathrm {я} \ зп х \ грех у}
- шишzзнак равно0⇔(потому чтоузнак равно0 а также грехИксзнак равно0)⇔(у∈{π/2+kπ∣k∈Z} а также Иксзнак равно0){\ displaystyle \ cosh z = 0 \ Leftrightarrow \ left (\ cos y = 0 {\ text {et}} \ sinh x = 0 \ right) \ Leftrightarrow \ left (y \ in \ {\ pi / 2 + k \ pi \ mid k \ in \ mathbb {Z} \} {\ text {and}} x = 0 \ right)}.
 {2} -1}}}.}
{2} -1}}}.}использовать
Физический
Репрезентативная кривая функции на описывает цепь, то есть форму однородного троса, закрепленного на обоих концах и подверженного действию силы тяжести. шиш{\ displaystyle \ cosh}
Архитектура
Gateway Arch в Сент — Луисе, штат Миссури .
Гиперболический косинус по архитектуре соответствует дуге цепной передачи, изначально возникшей в результате проектирования подвесных мостов . Антони Гауди был одним из первых, кто широко использовал его в общей архитектуре, в частности, с двумя из его самых известных работ: склепом Колония Гуэль и Саграда Фамилия .
Gateway Arch в Сент — Луисе в Миссури имеет форму перевернутой цепной линии. Он возвышается на 192 м в центре и на 192 м в основании. Точки этой арки приблизительно удовлетворяют уравнению
- узнак равно-39шиш(Икс39)+231{\ displaystyle y = -39 \ cosh \ left ({\ frac {x} {39}} \ right) +231}
для –96 < x <96 .

Примечания и ссылки
- ↑ Международный стандарт ISO / IEC 80000-2 : 2009 рекомендует кос .
Смотрите также
- Гиперболический синус
- Гиперболический тангенс
Тригонометрия
Круговая тригонометрия Тригонометрические функции - Косинус
- Синус
- Касательная
- Котангенс
- Секант
- Косеканс
- синус разливается
Взаимные круговые функции - Арккосинус
- Синусовая дуга
- Касательная дуга
- Котангенс дуги
- Секущая дуга
- Косекансная дуга
Тригонометрические интегралы - Интегральный косинус
- Интегральный синус
Отношения - Тригонометрическая идентичность
- Пифагорейское тригонометрическое тождество
- Закон косинуса
- Закон синусов
- Закон касательных
- Закон котангенсов
Гиперболическая тригонометрия Гиперболическая функция - Гиперболический косинус
- Гиперболический синус
- Гиперболический тангенс
- Гиперболический котангенс
- Гиперболический секанс
- Гиперболический косеканс
Реципрокная гиперболическая функция - Обратный гиперболический косинус
- Реципрокный гиперболический синус
- Взаимный гиперболический тангенс
- Эллиптическая функция / Эллиптическая интегральная функция
- Сферическая тригонометрия
<img src=»https://fr.
 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ И ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
И
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Гиперболические функции
Определение
Гиперболические функции задаются следующими формулами:
(в англоязычной литературе обозначается )
(в англоязычной литературе обозначается )
(в англоязычной литературе обозначается )
Свойства
Связь с тригонометрическими функциями:
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

.
.
Важные соотношения:
Чётность:
Формулы сложения:
Формулы двойного угла:
Формулы кратных углов:
Произведения
Суммы
Формулы понижения степени
Производные:
Интегралы:
Неравенства:
Для всех выполняется:
Разложение в степенные ряды:
(Ряд Лорана)
Здесь — числа Бернулли.

Графики:
sh(x), ch(x), th(x), cth(x)
sh, ch и th
csch, sech и cth
Обратные гиперболические функции
— обратный гиперболический синус, гиперболический арксинус, ареасинус:
— обратный гиперболический косинус, гиперболический арккосинус, ареакосинус.
— обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс.
— обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс.
— обратный гиперболический секанс, гиперболический арксеканс, ареасеканс.
— обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс.
Графики:
arsh(x), arch(x), arth(x), arcth(x)
Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями:
где i — мнимая единица.
Эти функции имеют следующее разложение в ряд:
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Обратные гиперболические функции
Название функции Обозначение в русской литературе
Обозначение в английской литературе
ареасинус
arsh
arsinh, sinh−1
ареакосинус
arch
arcosh, cosh−1
ареатангенс
arth
artanh, tanh−1
ареакотангенс
arcth
arcotanh, cotanh−1
ареасеканс
arsech
arsech, sech−1
ареакосеканс
arcsch
arcsch, csch−1
Определения функций
Гиперболический ареасинус для действительного аргумента
Гиперболический ареакосинус для действительного аргумента
Гиперболический ареатангенс для действительного аргумента
Гиперболический ареакотангенс для действительного аргумента
Гиперболический ареасеканс для действительного аргумента
Гиперболический ареакосеканс для действительного аргумента
В комплексной плоскости функции можно определить формулами:
Разложение в ряд
Обратные гиперболические функции можно разложить в ряды:
Асимптотическое разложение arsh x даётся формулой:
Производные
Для действительных x:
Пример дифференцирования: если θ = arsh x, то:
Комбинация гиперболических и обратных гиперболических функций
Дополнительные формулы
Функция гиперболического косинуса — Статистические инструкции
Типы функций >
График e x , e -x и функции гиперболического косинуса ch(x), которая называется цепной связью.

Гиперболическая косинусная функция , обозначаемая chx и произносимая как рифмуется со словом «гош», является средним значением экспоненциальных функций e x и e -x , где e число Эйлера.:
Для традиционной функции косинуса с комплексным аргументом тождество равно 9.0018 cos( x ) = cos i x .
Производная ch(x) равна sinh(x), где sinh(x) — функция гиперболического синуса.
Свойства функций гиперболического косинуса
Cosh(x) является четной функцией (т. е. ch(- x ) = ch x ), что означает, что она симметрична относительно оси y.
Докажите, что функция гиперболического косинуса четна: cosh(-u) = cosh(u)
Посмотрите это видео на YouTube.
Функция гиперболического косинуса имеет область определения (-∞, ∞) и диапазон [1, ∞). Это функция , а не , тождественная функция; она не проходит тест горизонтальной линии, что означает, что функция необратима, если не применяется соответствующее ограничение области (например, x ≥ 0).
 Поскольку функция возрастает на отрезке [0, ∞), она имеет обратную функцию для этой области.
Поскольку функция возрастает на отрезке [0, ∞), она имеет обратную функцию для этой области.Функции гиперболического косинуса и гиперболического синуса имеют некоторые общие важные свойства [1]:
История и использование функции гиперболического косинуса
Функция гиперболического косинуса вычисляет гиперболический косинус угла. Это пример гиперболической тригонометрической функции, меры которой основаны на гиперболе, а не на единичной окружности, которая является основой для «обычных» тригонометрических функций. Это было примерно с 1700-х годов, когда оно появилось в работах многих выдающихся математиков, таких как Якопо Риккати (1759 г.) и Иоганн Ламберт (1768 г.). Он используется в качестве меры расстояния в некоторых типах неевклидовой геометрии и имеет множество приложений в реальной жизни, особенно в инженерии. Например, он может описывать кривую, образованную высоковольтной линией электропередач, подвешенной между двумя опорами [2].
 Архитекторы Ээро Сааринен и Ханнскари Бандал использовали функцию гиперболического косинуса для проектирования Арки Ворот в Сент-Луисе [3].
Архитекторы Ээро Сааринен и Ханнскари Бандал использовали функцию гиперболического косинуса для проектирования Арки Ворот в Сент-Луисе [3].Ссылки
[1] May, J. Раздел 4.5 Гиперболические функции. Получено 19 декабря 2021 г. с: https://www.math.uh.edu/~jen/winter%20mini/Notes/filled%20in%20notes/1431S45fi.pdf
[2] Encyclopedia Brittanica. Контактная сеть.
[3] Гиперболические функции. Получено 23 декабря 2021 г. с: http://www.math.udel.edu/~angell/hyper.pdfУКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Функция гиперболического косинуса» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/hyperbolic-cosine-function/Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

гиперболических функций в КАТАЛОГЕ
гиперболических функций в КАТАЛОГЕГиперболические функции
Гиперболические функции доступны только из КАТАЛОГА. В таблице ниже перечислены гиперболические функции в том порядке, в котором они появляются среди других пунктов меню CATALOG. Многоточие в таблице указывает на наличие дополнительных элементов CATALOG.
…
кош(
Гиперболический косинус
кош-1(
Гиперболический арккосинус
.
 ..
..грех(
Гиперболический синус
синх-1(
Гиперболический арксинус
…
танх(
Гиперболический тангенс
танх-1(
Гиперболический арктангенс
.


 {2} +1} {2 \ mathrm {e}}}} ;
{2} +1} {2 \ mathrm {e}}}} ;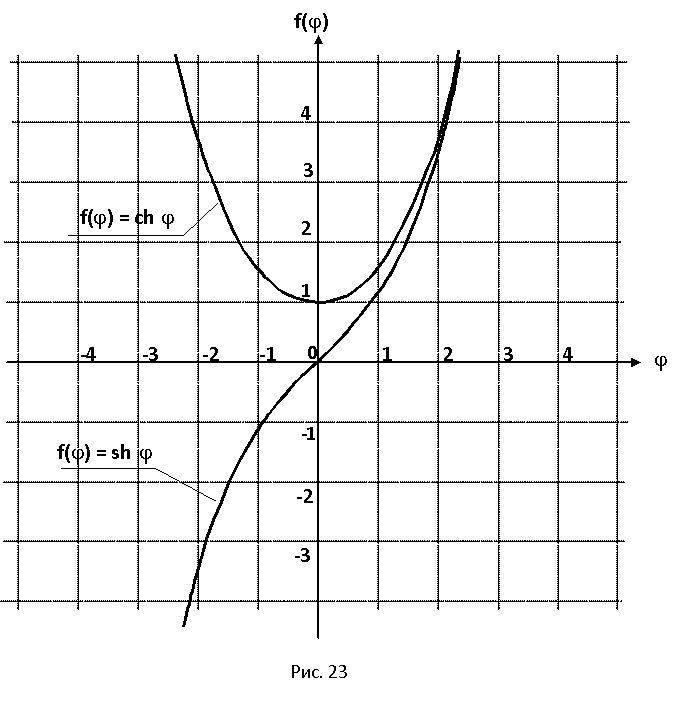 {2} -1}}}.}
{2} -1}}}.}
 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>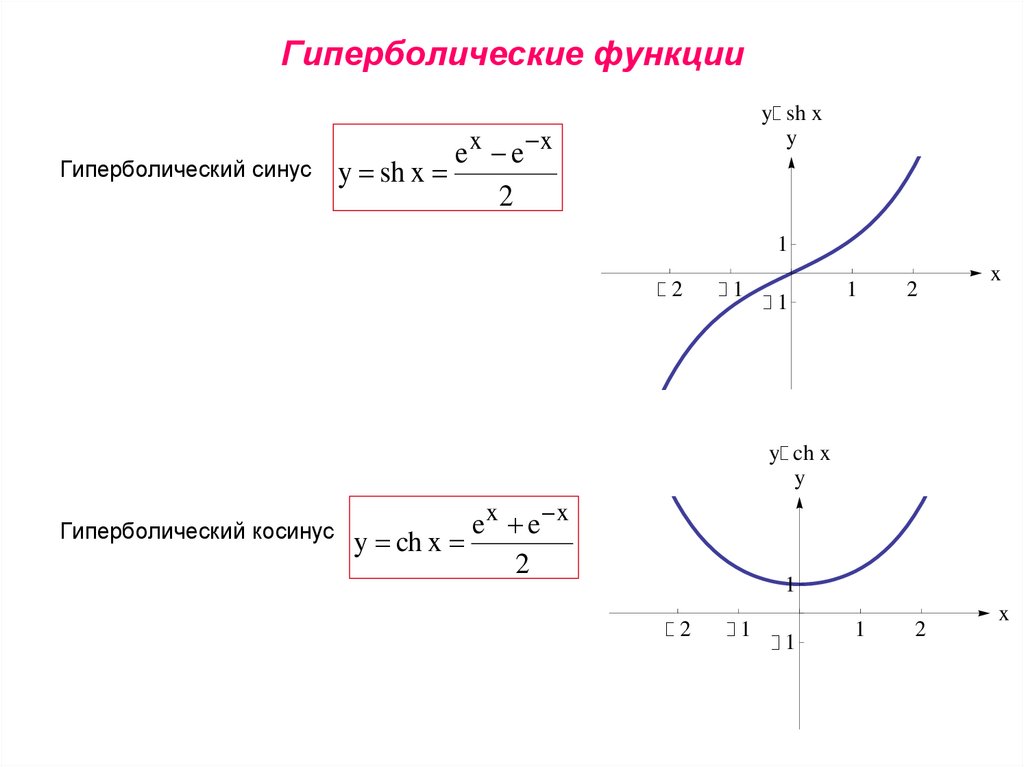

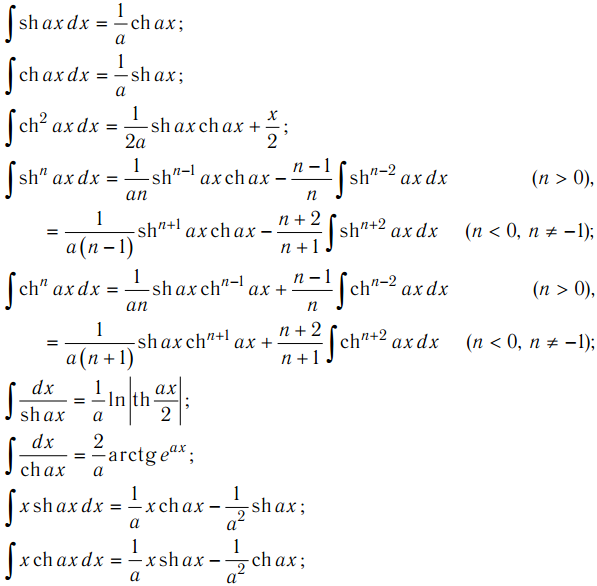 Поскольку функция возрастает на отрезке [0, ∞), она имеет обратную функцию для этой области.
Поскольку функция возрастает на отрезке [0, ∞), она имеет обратную функцию для этой области. Архитекторы Ээро Сааринен и Ханнскари Бандал использовали функцию гиперболического косинуса для проектирования Арки Ворот в Сент-Луисе [3].
Архитекторы Ээро Сааринен и Ханнскари Бандал использовали функцию гиперболического косинуса для проектирования Арки Ворот в Сент-Луисе [3].
 ..
..