Связь градусов и радиан. Как перевести радианы в градусы
Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов. Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.
Как работает функция индекс в Excel?
ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.
Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.
Появляется окно, в которое нужно ввести аргументы функции.
Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.
В 180 градусах будет 3,1415 радиан.
Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.
В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.
Как перевести Радианы в Градусы средствами Excel
ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus° . Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.
Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.
Появляется окно в которое нужно ввести аргументы функции.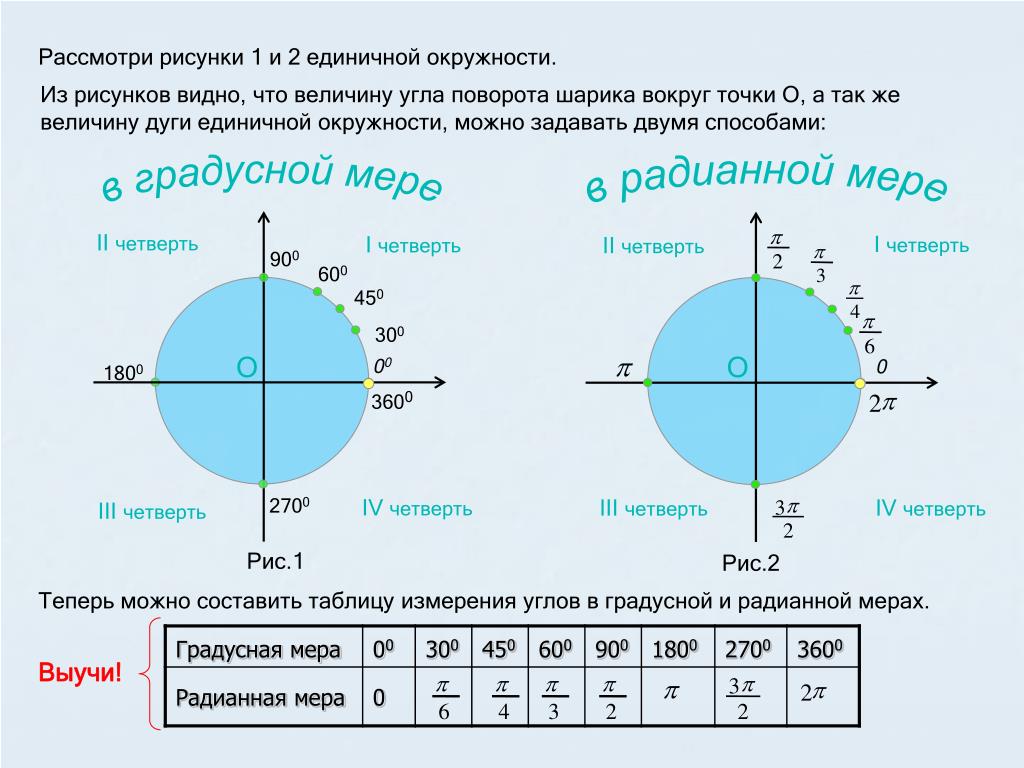
Вводим значение 4,1, так как нам следует найти сколько будет gradus°
в 4,1 rad
. Нажимаем ОК.
Для исходного значения 4,1 получаем ровно 235 градусов.
Таким образом выполняется перевод из радиан в градусы в Excel.
Сколько радиан в нескольких значениях градуса?
ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.
Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке. Указываем на высветившуюся функцию.
Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид.
Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.
Что такое градусы?
Градус — общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления. Градус тоже делится на 60 минут, а минуты — на 60 секунд. Общепринятыми обозначениями являются:
° — угловые градусы
’ — минуты,
’’ — секунды.
За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники — от картографии до расчета орбит искусственных спутников Земли.
Что такое радианы?
Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра. Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби.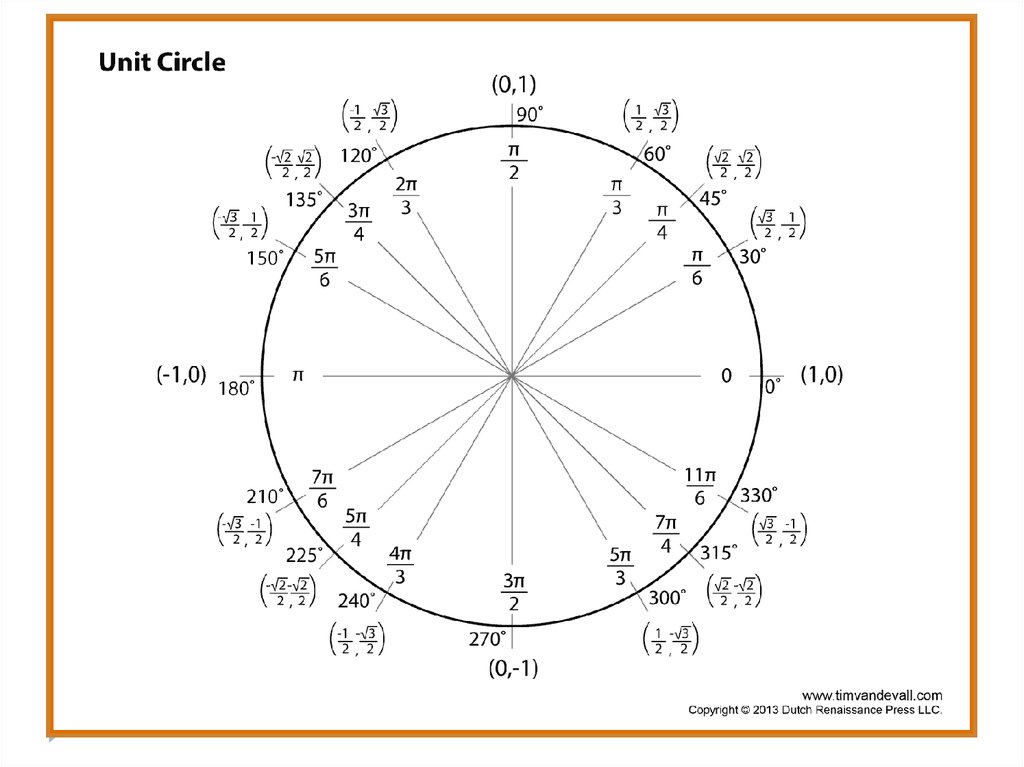
Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.
Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.
По определению, радиан — угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности. Международное обозначение радиана — rad, отечественное — рад. Размерности он не имеет.
Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.
Зачем понадобилось вводить новую единицу измерения угла?
Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века.
Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.
Как переводить градусы в радианы
Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.
И простая формула перевода из радианов в градусы: 1 рад = 180/π.
Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.
Остались вопросы?
Ответы на них можно найти , где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер паропроницаемости и скорости переноса пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.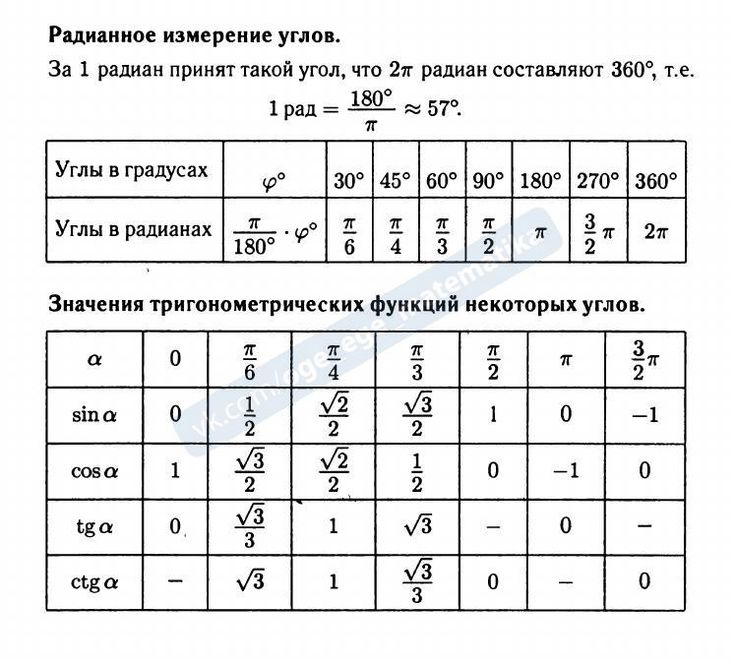
1 радиан [рад] = 57,2957795130823 градус [°]
Исходная величина
Преобразованная величина
градус радиан град гон минута секунда зодиакальный сектор тысячная оборот окружность оборот квадрант прямой угол секстант
Общие сведения
Плоский угол — геометрическая фигура образованная двумя пересекающимися линиями. Плоский угол состоит из двух лучей с общим началом, и эта точка называется вершиной луча.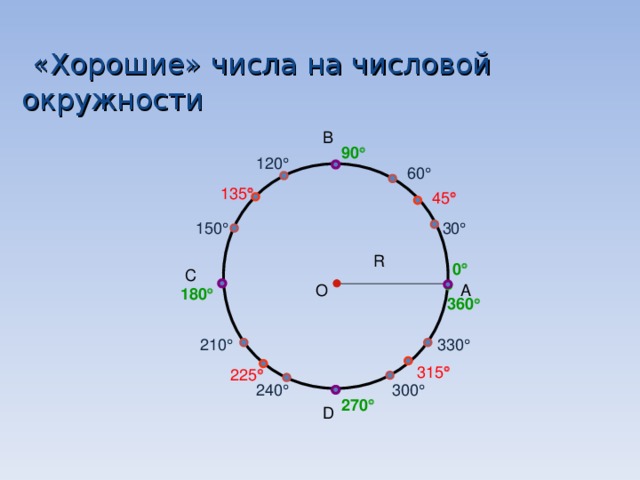
Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Виды углов
Прямые углы равны 90°, острые — меньше 90°, а тупые — наоборот, больше 90°. Углы, равные 180° называются
Когда сумма двух углов равна 90°, то есть один угол дополняет другой до 90°, они называются дополнительными . Если они дополняют друг друга до 180°, они называются смежными , а если же до 360° — то сопряженными . В многоугольниках углы внутри многоугольника называются внутренними, а сопряженные с ними — внешними.
Два угла, образованные при пересечении двух прямых и не являющихся смежными, называются вертикальными .
Они равны.
Измерение углов
Углы измеряют с помощью транспортира или вычисляют по формуле, измерив стороны угла от вершины и до дуги, и длину дуги, которая эти стороны ограничивает. Углы обычно измеряют в радианах и градусах, хотя существуют и другие единицы.
Можно измерять как углы, образованные между двумя прямыми, так и между кривыми линиями. Для измерения между кривыми используют касательные в точке пересечения кривых, то есть в вершине угла.
Транспортир
Транспортир — инструмент для измерения углов. Большинство транспортиров имеют форму полукруга или окружности и позволяют измерить углы до 180° и до 360° соответственно. В некоторых транспортирах встроена дополнительная вращающаяся линейка для удобства в измерении. Шкалы на транспортирах наносят чаще в градусах, хотя иногда они бывают и в радианах. Транспортиры чаще всего используют в школе на уроках геометрии, но их также применяют в архитектуре и в технике, в частности в инструментальном производстве.
Использование углов в архитектуре и искусстве
Художники, дизайнеры, мастера и архитекторы издавна используют углы для создания иллюзий, акцентов и других эффектов. Чередование острых и тупых углов или геометрические узоры из острых углов часто используются в архитектуре, мозаике и витражах, например в строении готических соборов и в исламской мозаике.
Одна из известных форм исламского изобразительного искусства — украшение с помощью геометрического орнамента гирих. Этот рисунок применяют в мозаике, резьбе по металлу и дереву, на бумаге и на ткани. Рисунок создается с помощью чередования геометрических фигур. Традиционно используют пять фигур со строго определенными углами из комбинаций в 72°, 108°, 144° и 216°. Все эти углы делятся на 36°. Каждая фигура разделена линиями на несколько более маленьких симметричных фигур, чтобы создать более тонкий рисунок. Изначально гирихом назывались сами эти фигуры или кусочки для мозаики, отсюда и пошло название всего стиля.
В исламском изобразительном искусстве и архитектуре часто используется руб аль-хизб — символ в форме одного квадрата, наложенного на другой под углом в 45°, как на иллюстрациях. Он может быть изображен как сплошная фигура, или в виде линий — в этом случае этот символ называется звездой Al-Quds (аль кудс). Руб аль-хизб иногда украшают небольшими кругами на пересечении квадратов. Этот символ используют в гербах и на флагах мусульманских стран, например на гербе Узбекистана и на флаге Азербайджана. Основания самых высоких в мире на момент написания (весна 2013) башен близнецов, башен Петро́нас построены в форме руб аль-хизба.
Острые углы часто используют в архитектуре как декоративные элементы. Они придают зданию строгую элегантность. Тупые углы, наоборот, придают зданиям уютный вид. Так, например, мы восхищаемся готическими соборами и замками, но они выглядят немного печально и даже устрашающе. А вот дом себе мы скорее всего выберем с крышей с тупыми углами между скатами. Углы в архитектуре также используют для укрепления разных частей здания. Архитекторы проектируют форму, размер и угол наклона в зависимости от нагрузки на стены, нуждающиеся в укреплении. Этот принцип укрепления с помощью наклона использовали еще с древних времен. Например, античные строители научились строить арки без цемента и иных связующих материалов, укладывая камни под определенным углом.
Обычно здания строят вертикально, но иногда бывают исключения. Некоторые здания специально строят с наклоном, а некоторые наклоняются из-за ошибок.
Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».
Иногда наклон здания — результат ошибки в проектировании, как например наклон Пизанской башни. Строители не учли структуру и качество почвы, на которой ее возводили. Башня должна была стоять прямо, но плохой фундамент не смог поддерживать ее вес и здание осело, покосившись на один бок. Башню много раз реставрировали; самая последняя реставрация в 20-м веке остановила ее постепенное оседание и увеличивающийся наклон. Ее удалось выровнять с 5.
5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Как перевести радианы в градусы c
141 — Перевод градусов в радианы и тригонометрические функции / MSDN rus / Visual C++
Шаг 141 — Перевод градусов в радианы и тригонометрические функции
Большинство тригонометрических функций который присутствуют в библиотеках таких как например math.h используют радианы. Например, функция sin:
Соответственно градусы нужно будет преобразовывать к радианам. Формула преобразования довольно простая. Для того, чтобы преобразовывать градусы в радианы, умножьте градусы на pi/180.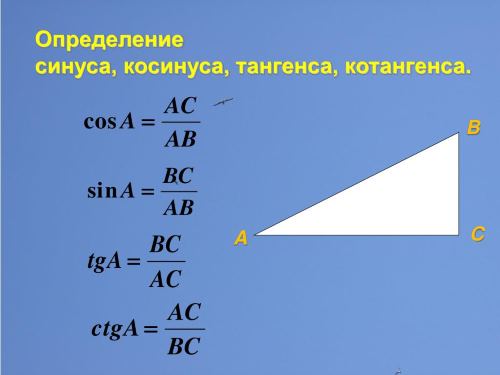
Для того, чтобы преобразовывать радианы в градусы, умножьте радианы на 180/pi. Давайте посмотрим пример:
Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .
Также можно выразить один градус в радианах.
1 ° = π 180 р а д
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °
Значит, в одном радиане примерно 57 градусов
1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д
Один градус содержит 0,0175 радиана.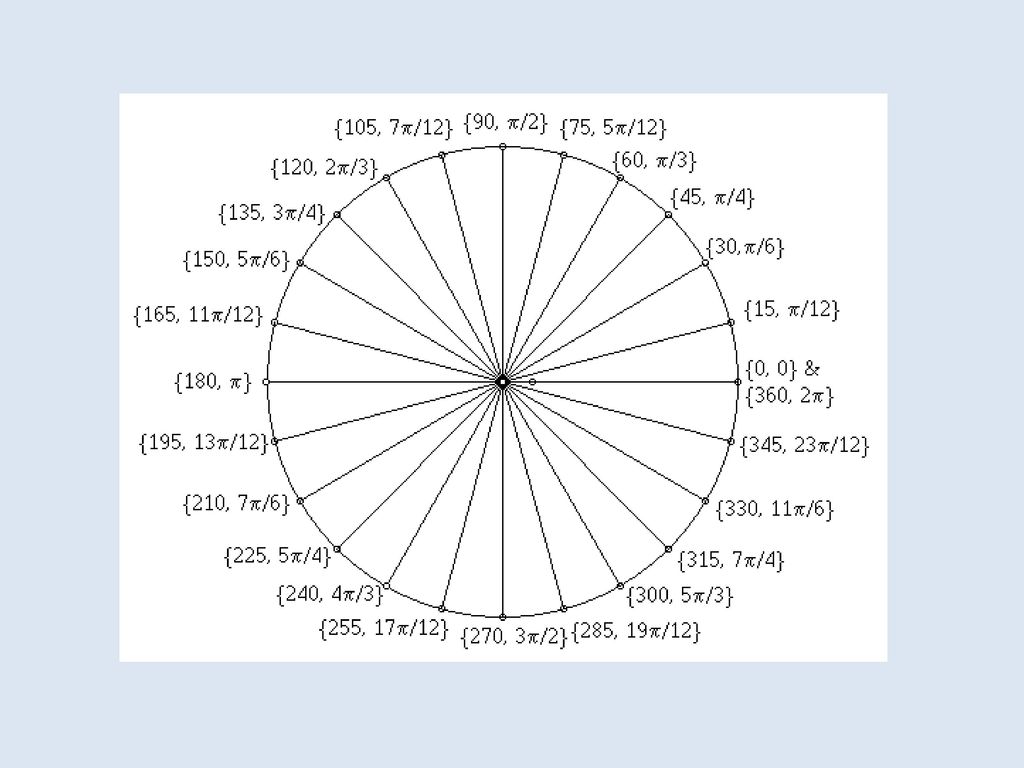
Формула перевода радианов в градусы
x р а д = х · 180 π °
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °
Градусы — радианы
Онлайн конвертер для перевода градусов в радианы и обратно
Теория
Угол — это геометрическая фигура, которая образована двумя лучами, выходящими из одной точки.
Радиа́н — угол, соответствующий дуге, длина которой равна её радиусу. Своё название данная едииница измерения получила от слова радиус. Имеет обозначение: рад, международное: rad.
Радианы являются основной единицей используемой в вичислениях.
Градус — общепринятая единица измерения плоского угла, которая равняется 1/90 части прямого угла или 1/360 часть окружности.
В отличии от радиан, градусы являются чисто символическими единицами измерения, так сказать «взятые с потолка» и не имеют в своём значении ни какого математического основания.
Причина выбора градуса в качестве единицы измерения углов неизвестна. В быту измерение углов в градусах выглядит удобнее и понятнее, но что касается математических вычислений, то здесь основными единицами являются радианы.
Как преобразовать градусы в радианы
Чтобы преобразовать градусы в радианы, умножьте угол на коэффициент преобразования.
Так как один градус равен 0,017453 радиана, вы можете использовать эту простую формулу для преобразования:
радиана = градусы × 0,017453
Угол в радианах равен градусам, умноженным на 0,017453.
Например, вот как преобразовать 5 градусов в радианы, используя приведенную выше формулу.
5° = (5 × 0,017453) = 0,087266 рад
Поскольку пи радианы равны 180°, эта формула преобразования предпочтительнее, поскольку она более точна и удобна в высшей математике.
радианы = градусы × π180
Другими словами, угол в радианах равен произведению градусов на число пи, деленному на 180.
Чтобы использовать эту формулу, начните с добавления градусов к формуле. Затем переместите градусы в начало дроби. Затем упростите дробь.
Например, давайте преобразуем 5 градусов в радианы, используя предпочтительную формулу.
радиан = 5° × π180
радиан = 5° × π180
радиан = 1 × π36
радиан = 136π
Градусы и радианы — это единицы измерения угла. Продолжайте читать, чтобы узнать больше о каждой единице измерения.
Градусы
Градус — это мера угла, равная 1/360 оборота или окружности. Число 360 имеет 24 делителя, поэтому с ним довольно легко работать. В персидском календарном году также 360 дней, и многие предполагают, что ранние астрономы использовали 1 градус в день.
Градус – это единица измерения угла, принятая в системе СИ для использования в метрической системе. Степень иногда также называют степенью дуги, степенью дуги или степенью дуги. Градусы могут быть сокращены до °, а также иногда сокращены до градусов. Например, 1 градус может быть записан как 1° или 1 градус.
Градусы также могут быть выражены в минутах и секундах в качестве альтернативы использованию десятичной формы. Минуты и секунды выражаются с помощью символов штриха (′) и двойного штриха (″), хотя для удобства часто используются одинарные и двойные кавычки.
Одна минута равна 1/60 градуса, а одна секунда равна 1/60 минуты.
Транспортиры обычно используются для измерения углов в градусах. Это полукруглые или полнокруглые устройства с градусной маркировкой, позволяющие пользователю измерять угол в градусах. Узнайте больше о том, как использовать транспортир, или загрузите транспортир для печати.
Радианы
Радиан — это мера угла, равная отношению начала и конца дуги к радиусу окружности или дуги.
1 радиан равен 180/π, или примерно 57,29.578°. В окружности примерно 6,28318 радиан.
Радиан – это производная единица измерения угла в системе СИ. Радианы могут быть сокращены как rad, а также иногда сокращены как c, r или R. Например, 1 радиан может быть записан как 1 rad, 1 c, 1 r или 1 R.
Радианы часто выражаются с помощью их определение. Формула для нахождения радианов: θ = s/r, где угол в радианах θ равен длине дуги s, деленной на радиус r. Таким образом, радианы также могут быть выражены в виде формулы длины дуги по радиусу.
Угол α в радианах равен углу α в градусах, умноженному на константу Пи, деленному на 180 градусов:
В настоящее время у нас есть около 5613 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеры и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.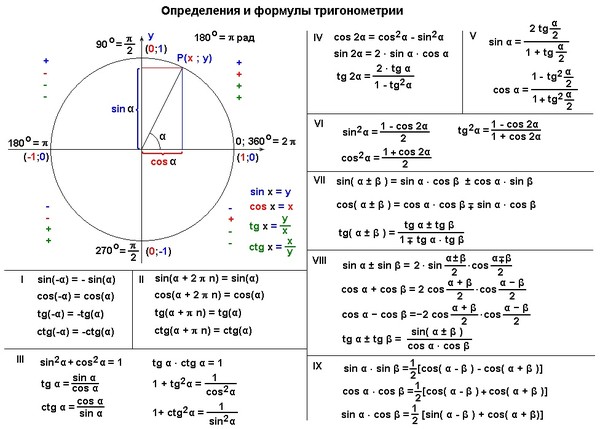
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика Инструменты Текст 3 Текст 3 Инструменты Текст 3
- Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Бесплатные онлайн-инструменты для преобразования энергии
- Бесплатные онлайн калькуляторы преобразования длины
- Бесплатные онлайн инструменты преобразования чисел
- Бесплатные онлайн калькуляторы преобразователя мощности
- Бесплатные онлайн инструменты преобразования температуры
- Бесплатные онлайн инструменты преобразования веса
- Бесплатные онлайн инструменты преобразования напряжения
- Бесплатные онлайн инструменты преобразования частоты
- Бесплатные онлайн-инструменты для преобразования цвета
- Бесплатные онлайн-инструменты для преобразования изображений
- Бесплатные онлайн-инструменты для электрических расчетов
- Калькуляторы преобразования электрического заряда
- Конвертер текста ASCII в двоичный код бесплатно онлайн
- Конвертер текста ASCII в шестнадцатеричный код бесплатно онлайн конвертер
- Бесплатный онлайн-конвертер двоичного кода в текст ASCII
- Бесплатный онлайн-конвертер двоичного кода в десятичный
- Бесплатный онлайн-конвертер двоичного кода в шестнадцатеричный
- Конвертер двоичного кода в строку
- Бесплатный онлайн конвертер дат в римские цифры
- Бесплатный онлайн конвертер десятичных чисел в двоичные
- Бесплатный онлайн конвертер десятичных чисел в дроби
- Бесплатный онлайн конвертер десятичных чисел в шестнадцатеричные
- Градусы в градусы, минуты, секунды бесплатно онлайн конвертировать
- Градусы в радианы бесплатно онлайн конвертировать
- Градусы, минуты, секунды в градусы бесплатно онлайн конвертировать
- Бесплатный онлайн-конвертер дробей в десятичные
- Бесплатный онлайн-конвертер дробей в проценты
- Бесплатный онлайн-конвертер шестнадцатеричных, десятичных, восьмеричных и двоичных чисел
- Бесплатный онлайн-конвертер шестнадцатеричных чисел в текст ASCII бесплатный онлайн-конвертер
- Как преобразовать двоичное число в десятичное
- Как преобразовать двоичное число в шестнадцатеричное
- Как преобразовать десятичное число в двоичное
- Как преобразовать десятичное число в дробь
- Как преобразовать десятичное число в шестнадцатеричное
- Как преобразовать градусы в радианы
- Как преобразовать дробное число в десятичное
- Как преобразовать шестнадцатеричное число в двоичное
- Как преобразовать шестнадцатеричное число в десятичное
- Как преобразовать число в римские цифры
- Как преобразовать проценты в ppm
- Как преобразовать ppm в проценты
- Как преобразовать радианы в градусы
- Как преобразовать римские цифры в число
- Бесплатный онлайн-конвертер восьмеричных чисел в десятичные
- Конвертер процентов в десятичные бесплатно онлайн
- Конвертер процентов в дроби бесплатный онлайн конвертер
- Конвертер процентов в ppm бесплатный онлайн конвертер
- ppb в ppm бесплатный онлайн конвертер
- ppm бесплатный онлайн конвертер
- ppm в проценты бесплатный онлайн конвертер
- 4
- 4
- ppm в ppm ppb бесплатный онлайн конвертер
- ppm в ppt бесплатный онлайн конвертер
- ppt в ppm бесплатный онлайн конвертер
- радианы в градусы бесплатный онлайн конвертер
- римские цифры бесплатный онлайн конвертер
- Бесплатный онлайн-конвертер научной записи
- Конвертер строки в двоичный код
И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Конвертер градусов в радианы Программа TI-84 — Калькулятор математических классов
Отсюда вы можете бесплатно загрузить программу на свой компьютер, а затем на свой калькулятор. (не волнуйтесь, мы проведем вас через это). Или вы можете использовать метод 2 и ввести код в калькулятор вручную. После этого продолжайте прокручивать эту страницу, чтобы узнать, что делает программа и как ее использовать.
Код конвертера градусов в радианы
Метод 1 (скачать)
1. Чтобы загрузить программу, нажмите на ссылку ниже.
Загрузить программу
2. Нажмите <здесь> , чтобы узнать, как установить программу на калькулятор после загрузки файла.
3. Продолжайте прокручивать, чтобы узнать, как работает программа и как ее использовать (необязательно).
4. В настоящее время программа хранится в оперативной памяти вашего калькулятора. Нажмите < здесь >, чтобы просмотреть руководство о том, как сохранить программу навсегда.
Способ 2 (Тип)
1. Посмотрите, как запустить программу на калькуляторе нажмите <здесь> (необязательно).
2. Начните вводить код, показанный на изображении ниже.
НЕ вводите по отдельности двоеточие или имя « PROGRAM:EXAMPLE », двоеточия появятся автоматически, когда вы начнете новую строку, нажав [ввод]. « ПРОГРАММА: ПРИМЕР » уже будет вверху.
Возникли проблемы с поиском символа или функции, которые вы видите в коде? См. , как ввести любую функцию/знак/символ на вашем TI-84 Plus>> .
*ВНИМАНИЕ*: Если вы очистите память своего калькулятора, программа будет потеряна. Чтобы узнать, как сохранить вашу работу навсегда, нажмите <здесь> .
Как пользоваться программой
Для начала откройте программу. На главном экране нажмите [prgm] , затем перейдите к программе (моя называется « RADTODEG »). Затем нажмите [введите] , а затем снова [введите] .
Теперь вам будет предложено выбрать « РАДИАН В ГРАДУСОВ» или « РАДИАНОВ В РАДИАН ». Для выбора перейдите к опции и нажмите [ввод] или нажмите соответствующую цифру, либо [1] , либо [2] , чтобы выбрать из списка.