Newton Graphing Calculator Pro + Загрузка символьной математики
Newton Graphing Calculator Pro + Символьная математика
Официальное приложение и игра
Распространяется ApkOnline
Скачать APK
СКРИНШОТЫОПИСАНИЕ
Загрузите это приложение под названием Newton Graphing Calculator Pro + Symbolic Math.
Newton Graphing Calculator Pro + Symbolic Math — wizer, newton, образование, рейтинг контента — все (PEGI-3). Это приложение имеет рейтинг 5 от 1 пользователей, которые используют это приложение. Чтобы узнать больше о компании/разработчике, посетите веб-сайт Wizer, который ее разработал. Приложения com.wizer.newton.pro.apk можно загрузить и установить на устройства Android 4.0.x и выше. Последняя версия 5.3.6 доступна для скачивания. Загрузите приложение с помощью своего любимого браузера и нажмите «Установить», чтобы установить приложение. Обратите внимание, что мы предоставляем как базовые, так и чистые APK-файлы, а также более высокую скорость загрузки, чем APK Mirror. Это приложение APK было загружено более 538 раз в магазине. Вы также можете скачать APK-файл com.wizer.newton.pro и запустить его с помощью популярных эмуляторов Android.
Это приложение APK было загружено более 538 раз в магазине. Вы также можете скачать APK-файл com.wizer.newton.pro и запустить его с помощью популярных эмуляторов Android.
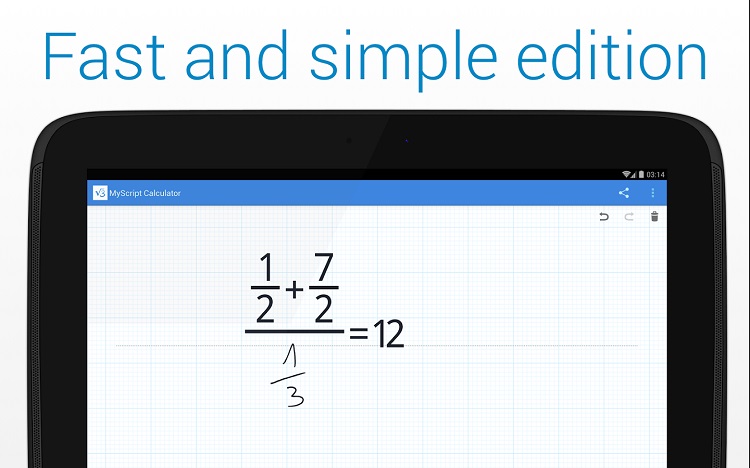
Почему это приложение? Мы считаем, что символьный математический или графический калькулятор должен быть таким же интуитивно понятным, как рукописный ввод, без накладных расходов на пользовательский ввод и сложный синтаксис. Например, обычно мы пишем «sin2x» на бумаге на уроке математики, а вводим «sin(2*x)» на калькуляторе. Разве не было бы замечательно просто ввести «sin2x»? Калькулятор Newton Graphing Calculator отображает 2D-кривую и 3D-поверхность с помощью математического ввода, такого как рукописный ввод. С нашим инновационным синтаксическим анализатором математический синтаксис так же прост, как когда вы пишете его в своей заметке. Двухмерный или трехмерный график автоматически распознается по количеству неизвестных переменных благодаря нашему мощному символьному математическому движку. После построения графика вы можете найти корни функций, отслеживать координаты, панорамировать или масштабировать 2D-график; рисовать контур, масштабировать или вращать 3D-график для беспрепятственного просмотра со всех сторон с помощью жеста руки, чтобы изучить математические свойства функции.Newton Graphing Calculator поставляется с прозрачным графиком, оптимизированной клавиатурой, меткой оси, легендой функции, палитрой цветов и отформатированной математической формулой, готовыми к продуктивному использованию. Полученный график и математическую формулу можно отправить по электронной почте, чтобы добавить в домашнее задание, поделиться с другом на Facebook, Line или Google+. Newton Graphing Calculator включает числовой калькулятор и средство решения уравнений с пошаговым решением, а также предварительный просмотр в реальном времени при вводе. Любимый ввод может быть сохранен в вашей математической коллекции, чтобы сэкономить время ввода. - Требуется разрешение на доступ к мультимедиа, чтобы сохранить захваченный график для совместного использования - Онлайн-справка http://www.wizerapp.net/newton_graphing_calculator_help.html • Явная функция, например, y=sin2x+3cosx • Неявная функция, например, sin(x2+y)=exp( -xy) • Параметрическая функция, например, x=sin2t/(2+t2) y=cos1t/(2+t2) • Полярная функция, например, r=1+2cosθ • Несколько функций, например, f=1sint/(2+t3) g=1cost /(2+t2) • Несколько параметрических функций • Поддержка разрыва, например, y=tanx • Имя переменной может быть любым символом, включая греческий символ (только версия Pro) • Явная функция, например, z=1sinx/(2+y2) • Неявная функция, например, x1 +y2+z2=2 • Контурная кривая явной функции, например, z=2sinx/(1+y2) • Параметрическая функция, например, x=sinv cosu y=sinv sinu z=cosv • Несколько функций, например, f=cosu sinv g=ucosv • Несколько функций параметрические функции • Трехмерная кривая x(t) y(t) z(t) • Имя переменной может быть любым символом, включая греческий • Интеграл, например, y=sin1x -> ∫sin2xdx = -cos3x/2 • Производная, например, y=sin2x -> y' = 2cos2x • Решить линейное уравнение, например, 2x+2=2 • Алгебра, комплексное число, полином, рациональная функция, двумерное и трехмерное пространство, метод Ньютона-Рафсона • Научный: pow sqrt root6 root4 abs exp log ln • Тригонометрический: sin cos tan cot asin acos atan acot • Гиперболический: sinh cosh tanh coth • Комплексное число, например (8i+ 2)(3i-3) ln(4i+2) • Числовая математика, например, 1/3 + 1/3 • Отображение цены акций, например, «акции Google», «Акции IBM Apple» • Отображение экономических данных, например, «нордический ВВП», « население азии", "безработица в Европе", "индекс потребительских цен в Азии", "китай, япония, ввп на душу населения" • Играйте в судоку: попробуйте "торт судоку", "судоку", "сложный судоку"
Обновления:
- • Радарная сетка для полярного графика
- • Обновите клавиатуру, чтобы анимировать обратную связь.

- • Играйте в судоку: попробуйте «судоку», «судоку», «сложную судоку», «сумасшедшую судоку».
- • Отображение данных из Всемирного банка: попробуйте «скандинавский ввп», «население Азии», «безработица в Европе», «азиатский индекс цен на дюйм», «китай-японский ввп на душу населения»
- • Интерфейс вопрос-ответ
- • Полноэкранный редактор графиков
- • Решите линейное уравнение, например, 6x + 4 = 8.
- • Интеграл, например, y = sin2x -> ∫sin2xdx = -cos2x / 2
- • Производная, например, y = sin2x -> y ‘= 2cos2x
Скачать APK
Newton Graphing Calculator Pro + Symbolic Math от ApkOnline.net
- <Пред
- Следующая>
Поиск Google научили понимать рукописный ввод // Смотрим
Профиль
Избранное
Google 27 июля 2012, 13:58 27 июля 2012, 14:58 27 июля 2012, 15:58 27 июля 2012, 16:58 27 июля 2012, 17:58 27 июля 2012, 18:58 27 июля 2012, 19:58 27 июля 2012, 20:58 27 июля 2012, 21:58 27 июля 2012, 22:58 27 июля 2012, 23:58
Для всех, кому сложно попадать по небольшим кнопочкам на экранной клавиатуре смартфона, а разговаривать с аппаратом кажется странным, Google ввел поддержку рукописного ввода для поисковых запросов. Опцию достаточно активировать в настройках поисковика в браузере мобильного устройства.
Опцию достаточно активировать в настройках поисковика в браузере мобильного устройства.
Для всех тех, кому сложно попадать по небольшим кнопочкам на экранной клавиатуре смартфона, а разговаривать с аппаратом кажется странным, Google ввел поддержку рукописного ввода для поисковых запросов. Никаких дополнительных плагинов не потребуется, достаточно активировать опцию в настройках поисковика в браузере мобильного устройства.
Новая функция поддерживается на смартфонах на базе Android 2.3 и выше, планшетах на Android 4.0 и выше, а также на всех устройствах на iOS 5. После активации режима ручного ввода в правом нижнем углу появляется индикатор, выполненный в виде написанной от руки буквы «g».
В своем официальном блоге Google пишет: «Представьте, что вы стоите на углу оживленной улицы, едете в трясущемся такси, разговариваете с другом, или просто работаете на планшете. Рукописный ввод позволяет вам искать в сети информацию, просто рисуя буквы пальцем практически в любом месте на экране.
Остается надеяться, что пользователи еще не совсем отвыкли писать буквы от руки. Функция рукописного ввода присутствует в большинстве современных телефонов, однако мало кто ей пользуется. Необходимо отметить, что поддержка рукописного ввода — это далеко не первый шаг корпорации в области альтернативных методов ввода данных. До этого Google широко продвигала возможности голосового набора поисковых запросов.
Также по теме:
Google добавила в поиск виртуальный калькулятор
Google стала провайдером сверхбыстрого интернета
Поиск Google научился строить графики функций
- новости
Весь эфир
Математическая доска | Совместная доска для преподавания и изучения математики
добро пожаловать в
Math Whiteboard — первая доска для совместной работы, разработанная специально для преподавания и обучения математике
БЕСПЛАТНО для учителей, репетиторов и студентов
Создайте доску или присоединитесь к ней прямо сейчас
партнервстроить математическую доску на свой сайт
Интеграция FluidMath
FluidMath — это инструмент для создания страниц MathWhiteboard.
Вы можете сохранять свои доски в FluidMath и обмениваться копиями на MathWhiteboard.com
Узнайте больше об этом здесь > Интеграция FluidMath
Поставьте лайк и следите за нами в Twitter и Facebook:
Твиттер Фейсбук
Привет любителям математической доски!
У нас есть новая страница в Facebook
Ставьте лайк и следите за нами здесь:
Фейсбук
Посетите вебинар MathWhiteboard с Эриком Куртсом
Учителя, репетиторы и ученики
Начните сотрудничество прямо сейчас! Нажмите кнопку ниже и общайтесь по математике самым естественным и плавным способом с помощью MathWhiteboard.
Создайте доску или присоединитесь к ней прямо сейчас
Партнеры
Вставьте MathWhiteboard на свой сайт и предоставьте своим пользователям наиболее гибкие возможности совместного преподавания и изучения математики. Нажмите кнопку ниже, чтобы узнать о партнерских отношениях.
партнер с mathwhiteboard
оживите математику!
Вот несколько замечательных вещей, которые вы можете делать с доской по математике
сотрудничать
Используйте совместное рабочее пространство по математике со своими учениками
графический калькулятор
Mathwhiteboard похож на умный лист математической бумаги со всеми функциями графического калькулятора
написать или ввести математику
Ввод математики прост благодаря распознаванию рукописного ввода, или вы можете просто ввести математику
Система компьютерной алгебры
Полная система компьютерной алгебры позволяет выполнять вычисления от арифметики до исчисления
импортировать pdf-файлы
Вы можете сделать файлы с заданиями в формате pdf фоном
работает в вашем браузере
Не требует установки, просто запускается в вашем браузере на любом устройстве, ChromeBook, iPad, планшете с Windows и т. д.
д.
И многое другое!
Технология MathWhiteboard запатентована: 9 576 495 долларов США; 9 691 294 США; 9 773 428 долларов США; 10 431 110 долларов США; США 11 282 410
примеры математической доски
системы уравнений
плавное перемещение между рукописными математическими формулами, графиками и решениями
анимация скорости изменения
Математические наброски позволяют связать абстрактные математические обозначения с конкретными примерами, оживляя нарисованные от руки наброски.
Вычисления
От простой арифметики до исчисления, под капотом находится мощная система компьютерной алгебры.
аннотировать PDF-файлы
Просто перетащите PDF-файлы на доску, а затем напишите сверху математические выражения и аннотации
Посмотреть больше примеров
Создание рукописного многоразрядного калькулятора | Нирав Гала
Использование сверточных нейронных сетей (Keras API с бэкендом Tensorflow)
Фото Markus Spiske на UnsplashЦель этой статьи:
- Создать модель CNN, которая может идентифицировать цифры и простые математические операторы из изображения
- Задайте математическое выражение и вычислите ответ
- Если он неверен, обновите модель правильным ответом
Чтобы легко следовать этой статье, я рекомендую сначала понять основы следующих тем:
- Машинное обучение с использованием Python
- Сверточные нейронные сети (см.
 это видео на YouTube от MIT 6.S191)
это видео на YouTube от MIT 6.S191) - Keras API 7 900 Это!
- Введение.
Сверточные нейронные сети — это подкласс алгоритмов глубокого обучения, которые в основном используются для анализа визуальных образов. Большие объемы обучающих данных, увеличивающиеся вычислительные мощности и передовые методы глубокого обучения проложили путь CNN для выполнения сложных визуальных задач [1].
Все началось в 1958 году, когда Дэвид Х. Хьюбел и Торстен Визель провели серию экспериментов, чтобы понять структуру зрительной коры (за что они получили Нобелевскую премию в 1981 году). Авторы обнаружили, что некоторые нейроны имеют более крупные рецептивные поля и реагируют на сложные паттерны, представляющие собой комбинацию паттернов более низкого уровня, обнаруживаемых другими нейронами. Эти наблюдения привели к идее, что нейроны более высокого уровня основаны на выходах соседних нейронов более низкого уровня[2].

Эта мощная визуальная архитектура развивалась на протяжении многих лет, пока в статье Yann LeCun et al. в 1998 году сформулировал знаменитую архитектуру LeNet-5 . В этой статье было введено понятие сверточных и объединяющих слоев [2].
Сегодня многие компании используют CNN для анализа визуальных образов. Ниже приведены несколько примеров:
- Tesla для автопилота [3]
- Google Photos для классификации изображений [4]
- Исследования искусственного интеллекта Facebook (FAIR) для языкового перевода [5]
1.2 Объект
Цель этой статьи — показать вам, как построить модель CNN, которая может делать следующее :
Изображение автораМодель построена с помощью keras API (бэкэнд Tensorflow) с использованием Python .
Начиная со следующего раздела, я прошу вас сначала скопировать код раздела в вашу IDE, прежде чем читать раздел.
2.1 Подготовка набора данных
Набор данных, используемый для этого проекта, можно найти в здесь (имя файла dataset.
 csv ) . Это расширение набора данных MNIST, которое содержит 85 709 изображений арабских цифр (от 0 до 9) и математических операторов (+, -, * и /). Каждое изображение имеет размер 28 X 28 пикселей. Для удобства кодирования математические операторы обозначены следующим образом:
csv ) . Это расширение набора данных MNIST, которое содержит 85 709 изображений арабских цифр (от 0 до 9) и математических операторов (+, -, * и /). Каждое изображение имеет размер 28 X 28 пикселей. Для удобства кодирования математические операторы обозначены следующим образом:- 10 представляет «/» (деление)
- 11 представляет «+» (сложение)
- 12 представляет «-» (вычитание)
- 13 представляет «/» (умножение)
В первом фрагменте кода загруженная база данных загружается в виде кадра данных Pandas размером (85709 X 785). Метки (y) отделены от набора данных (X).
785 = 1 (метка) + 28 (высота в пикселях) * 28 (ширина в пикселях)
набор данных изменен, чтобы соответствовать стандартам 4D Tensor ([размер мини-пакета, высота = 28 пикселей, ширина = 28 пикселей, каналы = 1 из-за оттенков серого]).
Затем метки преобразуются из векторов классов (14 векторов классов) в бинарные матрицы классов (необходимые для обучения моделей Keras).

2 -> [0,0,1,0,0,0,0,0,0,0,0,0,0,0]
Наконец, данные разделены на обучение (90%) и проверку ( 10%). Теперь набор данных готов к использованию для обучения модели.
2.1 Построение и обучение модели CNN
Модель CNN построена с использованием класса последовательной модели Keras. В таблице ниже показан список слоев (и гиперпараметров), переданных для создания модели.
Изображение автораВходной и первый скрытый слой
- Во-первых, набор из двух сверточных слоев (32 фильтра и функция активации ReLU) для определения шаблонов изображения низкого уровня (линий, краев и т. д.). .).
- Затем уровень Max Pooling (размер пула 2 X 2) просто уменьшает количество фильтров, чтобы уменьшить вычислительную нагрузку, использование памяти и количество параметров.
- Наконец, Dropout используется в качестве метода регуляризации. Он случайным образом игнорирует 25% узлов во время каждой итерации обучения.

Второй скрытый слой
- Набор из двух сверточных слоев (64 фильтра и функция активации ReLU) для идентификации сложных паттернов, представляющих собой комбинацию низкоуровневых паттернов, обнаруженных первым слоем.
- Слой Max Pooling (размер объединения 2 X 2) для понижения дискретизации.
- Дропаут для регуляризации.
Полностью подключенный слой и выход
- Во-первых, слой Flatten используется для преобразования окончательных карт объектов в один 1D-вектор (необходим для ввода плотного слоя).
- Затем полносвязный (плотный) слой , который действует как искусственная нейронная сеть.
- Дропаут для регуляризации.
- Наконец, еще полносвязных (плотных) слоев с активацией Softmax в качестве выходного слоя. Функция softmax берет элементы выходного слоя и преобразует их в чистое выходное распределение вероятности каждого класса.
 Класс с наибольшей вероятностью принимается за предсказание модели.
Класс с наибольшей вероятностью принимается за предсказание модели.
После добавления слоев определяются параметры обучения (функция потерь, функция оценки и функция оптимизации).
Функция потерь измеряет частоту ошибок между наблюдаемыми и предсказанными метками. Для этой модели в качестве функции потерь используется categorical_crossentropy .
Затем известный RMSprop используется в качестве алгоритма оптимизатора для итеративного улучшения различных параметров модели. RMSprop также является одним из самых быстрых оптимизаторов.
Метрическая функция «точность» используется в качестве функции оценки для оценки производительности нашей модели.
Чтобы оптимизатор сходился быстрее и ближе всего к глобальному минимуму функции потерь, функция ReduceLROnPlateau из Keras.callbacks используется в качестве метода отжига скорости обучения (LR).

Во избежание переобучения набор данных расширяется за счет искусственного изменения существующего набора данных (масштабирование, смещение и т. д.). Этот процесс называется Data Augmentation и выполняется с использованием ImageDataGenerator от Keras.
Наконец, модель обучается на наборе данных с 5 эпохами и размером пакета 86.
ВЫВОД[]:
Эпоха 1/5
- 412 с - потеря: 0,2837 - точность: 0,9143 - val_loss: 0,0606 - val_accuracy1: 0,983
Эпоха 2/5
- 439 с - потеря: 0,0776 - точность: 0,9771 - val_loss: 0,0348 - val_accuracy: 0,99
EPOCH 4/5
- 413S - Потеря: 0,0578 - Точность: 0,9837 - val_loss: 0,0285 - val_accuracy: 0,9916
EPOCH 5/5
- 410S - Потеря: 0,0540 - Точность: 0,9845 - val_loss: 0,032 - 0,0540 - 0,9845 -val_loss: 0,032 222 222 2222 21.Обучение модели заняло около 35 минут и достигло точности проверки 99,17 % после 5-й эпохи.
Обученная модель теперь готова делать некоторые прогнозы! Модель (с ее обученной структурой и весами) также можно сохранить на вашем компьютере.

Примечание. Разделы 1 и 2 статьи основаны на этом Записная книжка Kaggle.
Теперь пришло время использовать обученную модель для анализа изображения рукописного математического выражения. Изображение (имя файла testing.png ), используемое в этом артсиеле, доступно в моем репозитории GitHub.
Изображение автора3.1 Разделение элементов
Для анализа математического выражения сначала необходимо разбить его на отдельные элементы, которые затем могут быть идентифицированы моделью.
Изображение автораДля этого файл изображения (3066 пикселей * 208 пикселей) сначала загружается в оттенках серого с помощью Pillow (PIL).
Затем размер изображения изменяется до высоты 28 пикселей (требование к вводу модели). Сохраняя то же соотношение сторон, ширина также регулируется.
Затем изображение преобразуется из PIL.Image в массив Numpy.
Изображение автора Фон меняется на черный путем вычитания 255, а изображение нормализуется по шкале серого путем деления на 255. Изображение выглядит примерно так.
Фон меняется на черный путем вычитания 255, а изображение нормализуется по шкале серого путем деления на 255. Изображение выглядит примерно так. Примечание. Используйте matplotlib.pyplot.imshow для отображения массивов в виде изображения
Теперь массив изображений разбит на отдельные массивы элементов. Это делается путем поиска в массиве изображений последовательных ненулевых столбцов и их группировки для формирования одного массива элементов. Все эти массивы элементов хранятся в одном списке. Поскольку в математическом выражении 14 элементов, размер списка равен 14.
In []: len(out)
Out[]: 14Чтобы идентифицировать элемент с помощью модели, важно иметь размер изображения 28px*28px. Высота уже 28px. Однако из-за процесса разделения ширина каждого элемента не равна точно 28 пикселям.
Поэтому после разделения ширина каждого элемента регулируется до 28 пикселей. путем добавления столбцов с нулевым значением (столбцы-заполнители) в массивы элементов.
Изображение автора
Этот процесс повторяется для всех элементов, пока все они не станут 28px *28px.
Изображение автораНаконец, список элементов преобразуется обратно в массив формы (14, 28, 28, 1), чтобы соответствовать входным требованиям модели 4D-тензора [mini_batch_size, высота, ширина, каналы].
In []: elements_array.shape
Out[]: (14, 28, 28, 1)Теперь этот массив элементов готов для модели!
3.2 Прогноз элементов
Массив элементов пропускается через модель для прогнозирования. Модель возвращает вероятности всех классов чисел (функция Softmax). Выбирается класс с наибольшей вероятностью.
In []: print(elements_pred)Out[]: [ 9 8 10 7 6 13 5 4 11 3 2 12 1 0]
Как видите, модель смогла правильно предсказать все элементы!
Следующим шагом является построение математического выражения из этих элементов и его вычисление. Давайте прямо в это.
Когда все отдельные элементы определены, пришло время создать математическое выражение и вычислить его.

Для создания математического выражения числовые классы (от 0 до 9) перегруппированы, чтобы сформировать многозначные числа. В то время как классы 10, 11, 12 и 13 преобразуются в операторы «/», «+», «-» и «*» соответственно.
Например:
[1 0] → Элементы класса 1 и 0 перегруппировываются, образуя число 10
[10] → Элементы класса 10 преобразуются в оператор «/»
Наконец, числа и операторы объединяются в строку, представляющую математическое выражение.
В []: m_exp_str = math_expression_generator(elements_pred)В []: print(m_exp_str)Выход[]: 98 / 76 * 54 + 32 - 10
Затем к строке применяется метод eval() для вычисления ответа.
In []: print(equation)Out[]: 98 / 76 * 54 + 32 - 10 = 91,63
Иногда из-за неправильных прогнозов, таких как «4++4», математические выражения неверны и, следовательно, eval () вызовет синтаксическую ошибку. Следовательно, используется метод обработки ошибок.
Вот и все.
 Многозначный рукописный калькулятор готов!
Многозначный рукописный калькулятор готов!Но подождите, что делать с неправильным прогнозом? Следующий раздел как раз об этом.
Что делает алгоритмы машинного обучения такими мощными, так это их способность учиться на своих ошибках. Для этого модель должна быть переобучена с правильной информацией.
При ложном прогнозе приведенный выше код запрашивает у пользователя правильное математическое выражение. Затем он сравнивает предсказанное с правильным выражением и идентифицирует элементы, которые были предсказаны неправильно.
Затем код обучает модель от второго скрытого слоя до выходного слоя, используя правильные данные (первый скрытый слой не обучается).
Обновленная модель сохраняется и может быть использована позже для улучшения прогнозов.
Эта статья призвана научить вас основам того, как модели CNN можно использовать для создания простых инструментов, таких как калькулятор. В будущем эти базовые концепции помогут вам выполнять комплексный анализ визуализации и создавать сложные модели.

Надеюсь, эта статья была вам полезна. Если у вас есть какие-либо вопросы или отзывы, просто оставьте комментарий. Ваше здоровье!
- Набор данных можно найти здесь
- Полный код можно найти здесь.
[1] «Сверточная нейронная сеть», Wikipedia . 3 декабря 2020 г., по состоянию на 9 декабря 2020 г. [Онлайн]. Доступно: https://en.wikipedia.org/w/index.php?title=Convolutional_neural_network&oldid=992073762.
[2] А. Жерон, Практическое машинное обучение с помощью Scikit-Learn, Keras и TensorFlow: концепции, инструменты и методы создания интеллектуальных систем . О'Рейли Медиа, Инк., 2019 г..
[3] «Автопилот AI», Tesla , 2020 г. https://www.tesla.com/autopilotAI (по состоянию на 09 декабря 2020 г.).
[4] «ML Практикум: Классификация изображений | Практика машинного обучения», 2020 г. https://developers.google.com/machine-learning/practica/image-classification (по состоянию на 09 декабря 2020 г.



 это видео на YouTube от MIT 6.S191)
это видео на YouTube от MIT 6.S191)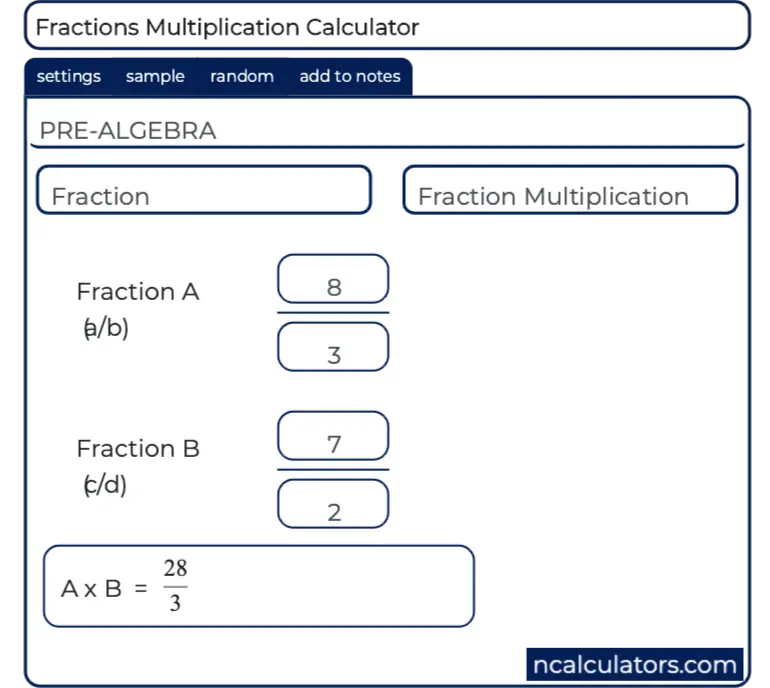
 csv ) . Это расширение набора данных MNIST, которое содержит 85 709 изображений арабских цифр (от 0 до 9) и математических операторов (+, -, * и /). Каждое изображение имеет размер 28 X 28 пикселей. Для удобства кодирования математические операторы обозначены следующим образом:
csv ) . Это расширение набора данных MNIST, которое содержит 85 709 изображений арабских цифр (от 0 до 9) и математических операторов (+, -, * и /). Каждое изображение имеет размер 28 X 28 пикселей. Для удобства кодирования математические операторы обозначены следующим образом:
 Класс с наибольшей вероятностью принимается за предсказание модели.
Класс с наибольшей вероятностью принимается за предсказание модели.

 Фон меняется на черный путем вычитания 255, а изображение нормализуется по шкале серого путем деления на 255. Изображение выглядит примерно так.
Фон меняется на черный путем вычитания 255, а изображение нормализуется по шкале серого путем деления на 255. Изображение выглядит примерно так. 

 Многозначный рукописный калькулятор готов!
Многозначный рукописный калькулятор готов!