построение графика, формула, знак модуля и примеры
Графики и формулы кусочно-линейных функций
Ситуация, когда движение или другое явление можно описать одной линейной функцией, определенной на интервале $-\infty \lt t \lt +\infty$, в действительности невозможна. Хотя бы потому, что возраст Вселенной велик, но не бесконечен.
На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т.п. Как задать подобную зависимость?
Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода.
Изобразим зависимость s(t) графически:
Первый отрезок AB легко записать: $ s_1 (t) = 5t,0 \le t \lt 2$
С отрезком BC тоже всё ясно: $s_2 (t) = 10,2 \le t \lt 3$
Осталось найти формулу для отрезка CD. Для него известен угловой коэффициент, равный скорости k = -4; знак «минус» оттого, что турист возвращается обратно. Формула имеет вид $s_3 (t) = -4t+b$. Также, нам известны координаты C(3;10).
Подставляем: $10 = -4 \cdot 3+b \Rightarrow b =22$. Осталось рассчитать момент возвращения:
$$0 = -4t_{back}+22 \Rightarrow t_{back} = 22:4 = 5,5$$ (ч)
Значит, формула движения на отрезке $CD:s_3 (t) = -4t+22,3 \le t \le 5,5.$
Получаем:
$$s(t) = {\left\{ \begin{array}{c} 5t,0 \le t \lt 2 \\ 10,2 \le t \lt 3 \\ -4t+22,3 \le t \le 5,5 \end{array} \right.} $$
Важным свойством заданной функции является выполнение условий согласования:
$$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$
Наша функция «сшита» на концах промежуточных интервалов.
В общем случае:
Функция вида
$$x f(x) = {\left\{ \begin{array}{c} k_1 x+b_1, x_1 \le x \lt x_2 \\ k_2 x+b_2,x_2 \le x \lt x_3 \\…\\ k_n x+b_n,x_n \le x \lt x_{n+1} \end{array} \right.}$$
называется кусочно-линейной.
При этом для функции на краях интервалов выполняются условия согласования:
$$f_i (x_{i+1} ) = f_{i+1} (x_{i+1} ),i = \overline {1,n-1} $$
Графиком кусочно-линейной функции является ломаная линия
Знак модуля в линейных функциях
По правилу раскрытия скобок модуля (см. §4 данного справочника)
$$ |x| = \left[ \begin{array}{cc} x, x\ge0 \\ -x, x \lt 0\end{array} \right.$$
Внимание!
Если в формуле для линейной функции содержится знак модуля, то после его раскрытия получается кусочно-линейная функция.
Например:
$$ y = 2|x|+5 = {\left\{ \begin{array}{c} -2x+5, x\ge0 \\ 2x+5, x \lt 0\end{array} \right.} $$
Мы заменили квадратную скобку со значением «или» на фигурную скобку со значением «и», поскольку именно смысл объединения — «и того, и другого» — вкладывается в определение кусочно-линейной функции .
Примеры
Пример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
а) $ y = |x| = {\left\{ \begin{array}{c} -x, x \lt0 \\ x, x \ge 0 \end{array} \right.}$
б) $ y = 2|x|-1 = {\left\{ \begin{array}{c} -2x-1, x \lt0 \\ 2x-1, x \ge 0 \end{array} \right.}$
в) $ y = |x+1| = {\left\{ \begin{array}{c} -x-1, x \lt0 \\ x+1, x \ge 0 \end{array} \right.}$
г) $ y = |x-2| = {\left\{ \begin{array}{c} -x+2, x \lt0 \\ x-2, x \ge 0 \end{array} \right.}$
Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
$$ y = |2|x|-1| = {\left\{ \begin{array}{c} |-2x-1|, x\lt0 \\ |2x-1|,x \ge 0 \end{array} \right.} = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x-1 \lt 0 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x-1 \ge 0 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x-1 \lt 0 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x-1 \ge 0 \\ x \ge 0\end{array} \right.} \end{array} \right.}= $$
$$ = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x \lt 1 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x \ge 1 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x \lt 1 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x \ge 1 \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} x \gt — \frac{1}{2} \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} x \le — \frac{1}{2} \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}x \lt \frac{1}{2} \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}x \ge \frac{1}{2} \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} -2x-1, x \le — \frac{1}{2} \\ 2x+1, — \frac{1}{2} \lt x \lt 0 \\ -2x+1, 0 \le x \lt \frac{1}{2} \\ 2x-1, x \ge \frac{1}{2} \end{array} \right.} $$
Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко.
Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования.
Шаг 1. Строим y = 2x-1
Шаг 2. Строим y = 2|x|-1 по правилу: |x| отражает часть графика для положительных $x \ge 0$ влево, зеркально относительно оси Y
Шаг 3. Строим y = |(2|x|-1)| по правилу: общий модуль отражает участок графика с отрицательными $y \lt 0$ вверх, зеркально относительно оси X
Или на одном графике:
График кусочно заданной функции | Алгебра
Построить график кусочно заданной функции — один из видов задания 23 из ОГЭ по математике.
Рассмотрим примеры построения таких графиков.
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
График данной функции состоит из трёх частей.
Значения x=3 и x=4 разбивают числовую прямую на три промежутка, на каждом из которых рассмотрим отдельную функцию.
Соответственно, прямые x=3 и x=4 разбивают координатную плоскость на три области.
Каждый из графиков строится в своей области и не должен выходить за её пределы.
Чтобы не нарушить это правило, можно прямые x=3 и x=4 (прямые, параллельные оси Oy) выделить на черновике тонкой линией либо пунктиром. В чистовой вариант, разумеется, их переносить не нужно.
Итак, рассмотрим на трёх промежутках три различные функции.
1) Если x<4, y=2x-2.
y=2x-2 — линейная функция. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки.
При x=0 y=2·0-2=-2, получили точку (0;-2).
При x=2 y=2·2-2=2, получили точку (2;2).
Обычно для построения графика оформляют таблицу:
Значения x можно брать, вообще говоря, любые. Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x<3.
2) Если 3≤x≤4, y=-3x+13.
y=-3x+13 — линейная функция. График — прямая. Для построения прямой берём две точки.
3) Если x>4, y=1,5x-5.
y=1,5x-5 — линейная функция. График — прямая. для построения прямой берём две точки.
Отметим каждую пару точек и проведём через них прямые, не забывая об ограничениях.
Получим график, состоящий их двух лучей и одного отрезка:
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через точки соединения двух частей графика, то есть при m=1 и m=4:
Ответ: 1; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥4, y=x²-10x+27.
y=x²-10x+27 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=1>0).
Ищем координаты вершины параболы.
Таким образом, (5;2) — вершина параболы.
Так как a=1, от вершины строим параболу y=x².
(Другой вариант — переписать правую часть формулы в виде y=(x²-10x+25)+2=(x-5)²+2 и построить график параллельным переносом графика y=x² на 5 единиц вправо вдоль оси Ox и на 2 единицы вверх вдоль оси Oy).
2) Если x<4, y=x-1.
y=x-1 — линейная функция. График — прямая. Для построения прямой берём две точки:
Хотя на x наложено условие x<4, для построения прямой можно брать любые значение. Главное — не забыть, что правее x=4 прямая не должна выходить.
Итак, график данной функции состоит из двух частей. Прямая x=4 разделяет плоскость на две полуплоскости. Справа от неё расположена часть параболы с вершиной в точке (5;2), слева — прямая:
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через вершину параболы и через точку соединения параболы и прямой, то есть при m=2 и m=3:
Ответ: 2; 3.
3) Построить график функции
и определить, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥-3, y=x²+4x+4.
y=x²+4x+4 — квадратичная функция. График — парабола ветвями вверх. Можно найти координаты вершины параболы и от вершины построить график функции y=x².
(Если заметить в правой части формулу квадрата суммы и переписать формулу функции y=(x+4)², то можно построить параболу параллельным переносом параболы y=x² на 4 единицы влево вдоль оси Ox).
2) Если x<-3,
— функция обратной пропорциональности. График — гипербола. Для построения гиперболы нужно взять несколько точек:
Таким образом, график данной функции состоит из двух частей. Справа от прямой x=-3 строим параболу с вершиной в точке (-2;0), слева — ветвь гиперболы:
Прямая y=m имеет с графиком одну или две общие точки при m=0 и m≥1:
Ответ: m=0 и m∈[1;∞).
Материал для подготовки к ЕГЭ (ГИА) по алгебре (9 класс) на тему: Методическое пособие «Построение кусочно заданных функций»
Методическое пособие по теме
«Построение кусочно-заданных функций»
Понятие о кусочных функциях. На различных участках числовой прямой функция может быть задана разными формулами. Например: y=f(x), где
f(x)= х2, -3х-2
2х+8, -20
Такие функции назовём кусочными. Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.
Наличие таких свойств как чётность, нечётность, нули функции, промежутки знакопостоянства, монотонность, ограниченность у кусочных функций устанавливается согласно общепринятым определениям, с учётом особенностей составляющих области определения и входящих функций.
Для того чтобы вычислить значение кусочной функции в заданной точке, необходимо, во-первых, определить, какой составляющей области определения принадлежит эта точка, а, во-вторых, найти значение входящей функции на этой составляющей.
Ответы:
1)Функция убывает на промежутке [-2; +∞).
2)Функция возрастает на промежутках (-∞; -2] и [0; 2].
3)f(x)≥0, если х=0 и |х|≥ 3⅓;
4)у > 0, если х
5)Прямая y=m имеет с графиком две общие точки при m=3 и m=-1;
6)Прямая y=m имеет с графиком одну общую точку при m=-2 и m>1.
Задания для самостоятельной работы:
1)Постройте график функции y=f(x), где
x-1, если х
f(x)=
-1/2x+3, если x ≥ -2.
Укажите промежуток, на котором функция убывает.
2)Постройте график функции у=f(x), где
1/4х2-1, если -2≤ х ≤ 2
f(x)= 2-х, если х > 2
х+2, если х
Укажите промежутки возрастания функции.
3)Постройте график функции у=f(x), где
-х2, если -2≤ х ≤ 2
f(x)= 3х-10, если х > 2
-3x-10, если х
При каких значениях х значения функции у= f(x) неотрицательны?
4)Постройте график функции у= f(x),где
(х+1)2, если х
f(x)=
1-х2, если х ≥0.
При каких значениях х выполняется неравенство у > 0?
5)Постройте график функции у= f(x),где
х2-4х-1, если х ≥ 4
f(x)=
-х2+4х-1, если х
При каких значениях m прямая y=m имеет с графиком этой функции две общие точки?
6)Постройте график функции у= f(x),где
4/х, если х ≤ -2
f(x)= х, если -2
х2-4х+4, если х > 1.
При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?
Чтобы построить график кусочной функции, нужно:
- Построить в одной системе координат графики входящих функций,
- Провести прямые x=a, x=a, x=a, где a-граничные точки,
- На каждой составляющей области определения (a, a), где i=1…n выбрать тот график, который соответствует входящей функции на этой составляющей.
- Выяснить значение функции в граничных точках.
Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.
f(x)= х2, -3х-2
2х+8, -20
Построение:
- у=х2
- -3х-2
- Выделить часть графика 1.
- У=2х+8
- -20
- Выделить часть графика 2.
Рассмотрим построение графиков кусочных функций.
Постройте график функции y=f(x), где
f(x)= -1/2х+3, если х2
х-4 ,х>2
Укажите промежуток, в котором функция убывает.
Построим в одной системе координат графики функций у=1/2х+3, если х2 и у=х-4 ,х>2
Графиками обеих функций являются прямые. Для построения достаточно двух точек.
у=1/2х+3, х2
х | 2 | 4 |
у | 2 | 1 |
у=х-4 ,х>2
Ответ: Функция убывает на промежутке (-;2]
Постройте график функции y=f(x), где
2-2×2, если 2
f(x)= x-1, если x>1
-x-1, если x
Укажите промежутки возрастания функции.
Первым графиком функции является парабола, ветви направлены вниз. Построим график функции на отрезке [-2;2]
Второй график у= х-1 –прямая.
Третий график тоже прямая у=-х-1
Ответ: Функция возрастает на промежутках[-1;0]
и [1;)
Постройте график функции у=f(x), где
х2-1, если х0
f(x)= (x-1)2 ,если х>0
При каких значениях х выполняется неравенство у0
1)Первым графиком является парабола. Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.
Вторым графиком является тоже парабола. Построим её часть (х>0)путем сдвига вдоль оси ох вправо на 1 графика у= х2.
Ответ: при у>0, x1
Постройте график функции у=f(x), где
-х2-4х-3, если x-1
f(x)= x+1, если -11
2/x, если х>1
При каких значениях m прямая у=m имеет с графиком этой функции две общие точки.
Построим в одной системе координат графики функций.
1) Первым графиком функции является часть параболы, ветви направлены
вниз. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/(-1·2)=-2, то у=-(-2)2-4·(-2)-3=1.Итак, вершина параболы
в точке с координатой (-2;1).
Найдём точки пересечения с осью OX;
у=0. -х2-4х-3=0
х1=-3
х2=-1
Точки пересечения с осью OX: (-3;0) и (-1;0).
Найдём точки пересечения с осью Oу:
х=0
у=-(0)2-4·0-3=3
Точки пересечения с осью OX: (0;3).
Найдём дополнительные точки
2) Второй график у= х+1 –прямая.
Построим часть прямой
3)Третьим графиком является гипербола.
Построим часть гиперболы при х>1
Ответ: прямая у=m имеет с графиком этой функции две общие точкипри m=0 и 1
Постройте график функции у=f(x), где
f(x)= -х2, если |х|1
x2-1если |х| >1
Укажите промежутки возрастания функции.
Раскрывая знак модуля данную систему можно записать в следующем виде:
f(x)= -х2, если -1х1
x2-1если , х >1
x
Графиками данных функций является парабола. Построим первый график.
у=-х2 ,если -1х1
x2-1если , х >1
x
х | 1 | 2 | 3 | 4 | -1 | -2 | -3 | -4 |
у | 0 | 3 | 8 | 15 | 0 | 3 | 8 | 15 |
Ответ: функция возрастает на промежутках(- ;-1] и [0;1]
Постройте график функции у=f(x), где
х2-4х+4, если x>1
f(x)= x, если -21
4/x, если х-2
При каких значениях m прямая у=m имеет с графиком этой функции одну общую точку?
Построим в одной системе координат графики функций.
1) Первым графиком функции является часть параболы, ветви направлены
вверх. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/2·1=2
у=22-4·2+4=0
Итак, вершина параболы
в точке с координатой (2;0).
Найдём точки пересечения с осью OX;
у=0
х2-4х+4=(х-2)2 ; х=0
Точки пересечения с осью OX: (0;2).
Найдём точки пересечения с осью Oу: х=0
у=02-4·0+4=4
Точки пересечения с осью OX: (0;4).
Найдём дополнительные точки
2) Второй график у= х –прямая, проходящая через начало координат.
Часть прямой, находящийся в 1 и 3 четверти.
3)Третьим графиком у=4/x, является гипербола, которая находится в 3 четверти.
Построим часть гиперболы при х-2
Ответ: прямая у=m имеет с графиком одну общую точку при m=-2 и m>1
Постройте график функции у=. При каких значениях х выполняется неравенство у3?
Область определения данной функции D(у)=(-;0)(0;2) (2;+).
Разложим числитель и знаменатель на множители дроби вынесением общего множителя за скобки. Дальше числитель разложим на множители по формуле
ax2+bx+c=a(x-x1)(x-x2)
Преобразуем дробь: у====-х-1
у=-х-1-линейная функция, графиком является прямая, рисунок 1
рис.1
Для того , чтобы ответить на вопрос
рассмотрим рисунок 2
Рис.2
Ответ: неравенство у3 выполняется при
-4х2.
Найдите все значения к, при которых прямая у=кх пересекает в трёх точках ломанную, заданную условием:
2х+4, если х
у= -2, если-33
2х-8,если х>3
Прямая y= kx пересекает в трех
различных точках эту ломаную, если ее угловой
коэффициент больше углового коэффициента
прямой, проходящей через точку –(3; -2), и
меньше углового коэффициента прямой,
парал. прямым у=2х+4 ,у=2х-8 .
Найдем угловой коэффициент прямой,
проходящей через точку (-3;-2)
-2=-3к, к=2/3
Угловой коэффициент k прямой, парал.
Прямой у=2х+8 , равен 2.
Ответ: прямая имеет с ломанной три общие точки при 2/3
Методическое пособие «Построение кусочно-заданных функций»
li{counter-increment:lst-ctn-kix_list_1-7}#doc6977624 ol.lst-kix_list_2-8.start{counter-reset:lst-ctn-kix_list_2-8 0}#doc6977624 .lst-kix_list_2-6>li{counter-increment:lst-ctn-kix_list_2-6}#doc6977624 .lst-kix_list_2-8>li:before{content:»» counter(lst-ctn-kix_list_2-8,lower-roman) «. «}#doc6977624 .lst-kix_list_1-1>li:before{content:»» counter(lst-ctn-kix_list_1-1,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-0{list-style-type:none}#doc6977624 .lst-kix_list_1-1>li{counter-increment:lst-ctn-kix_list_1-1}#doc6977624 ol.lst-kix_list_2-0.start{counter-reset:lst-ctn-kix_list_2-0 0}#doc6977624 ol.lst-kix_list_2-1{list-style-type:none}#doc6977624 ol.lst-kix_list_2-2{list-style-type:none}#doc6977624 ol.lst-kix_list_2-3{list-style-type:none}#doc6977624 ol.lst-kix_list_2-4{list-style-type:none}#doc6977624 ol.lst-kix_list_2-5{list-style-type:none}#doc6977624 .lst-kix_list_2-0>li:before{content:»» counter(lst-ctn-kix_list_2-0,decimal) «) «}#doc6977624 ol.lst-kix_list_1-2.start{counter-reset:lst-ctn-kix_list_1-2 0}#doc6977624 .lst-kix_list_1-2>li:before{content:»» counter(lst-ctn-kix_list_1-2,lower-roman) «. «}#doc6977624 .lst-kix_list_2-8>li{counter-increment:lst-ctn-kix_list_2-8}#doc6977624 .lst-kix_list_1-5>li:before{content:»» counter(lst-ctn-kix_list_1-5,lower-roman) «. «}#doc6977624 .lst-kix_list_2-3>li{counter-increment:lst-ctn-kix_list_2-3}#doc6977624 .lst-kix_list_1-8>li{counter-increment:lst-ctn-kix_list_1-8}#doc6977624 ol.lst-kix_list_1-7.start{counter-reset:lst-ctn-kix_list_1-7 0}#doc6977624 ol.lst-kix_list_2-7{list-style-type:none}#doc6977624 ol.lst-kix_list_2-6{list-style-type:none}#doc6977624 .lst-kix_list_2-3>li:before{content:»» counter(lst-ctn-kix_list_2-3,decimal) «. «}#doc6977624 .lst-kix_list_2-4>li:before{content:»» counter(lst-ctn-kix_list_2-4,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-8{list-style-type:none}#doc6977624 ol.lst-kix_list_1-5.start{counter-reset:lst-ctn-kix_list_1-5 0}#doc6977624 .lst-kix_list_1-4>li:before{content:»» counter(lst-ctn-kix_list_1-4,lower-latin) «. «}#doc6977624 ol.lst-kix_list_2-4.start{counter-reset:lst-ctn-kix_list_2-4 0}#doc6977624 ol.lst-kix_list_1-1.start{counter-reset:lst-ctn-kix_list_1-1 0}#doc6977624 .lst-kix_list_2-1>li{counter-increment:lst-ctn-kix_list_2-1}#doc6977624 .lst-kix_list_2-0>li{counter-increment:lst-ctn-kix_list_2-0}#doc6977624 ol.lst-kix_list_1-0.start{counter-reset:lst-ctn-kix_list_1-0 0}#doc6977624 ol.lst-kix_list_2-3.start{counter-reset:lst-ctn-kix_list_2-3 0}#doc6977624 .lst-kix_list_1-5>li{counter-increment:lst-ctn-kix_list_1-5}#doc6977624 .lst-kix_list_2-5>li:before{content:»» counter(lst-ctn-kix_list_2-5,lower-roman) «. «}#doc6977624 .lst-kix_list_1-0>li:before{content:»» counter(lst-ctn-kix_list_1-0,decimal) «. «}#doc6977624 .lst-kix_list_2-4>li{counter-increment:lst-ctn-kix_list_2-4}#doc6977624 .lst-kix_list_2-7>li:before{content:»» counter(lst-ctn-kix_list_2-7,lower-latin) «. «}#doc6977624 .lst-kix_list_1-8>li:before{content:»» counter(lst-ctn-kix_list_1-8,lower-roman) «. «}#doc6977624 .lst-kix_list_1-6>li{counter-increment:lst-ctn-kix_list_1-6}#doc6977624 .lst-kix_list_2-5>li{counter-increment:lst-ctn-kix_list_2-5}#doc6977624 ol.lst-kix_list_1-6.start{counter-reset:lst-ctn-kix_list_1-6 0}#doc6977624 ol.lst-kix_list_2-2.start{counter-reset:lst-ctn-kix_list_2-2 0}#doc6977624 .lst-kix_list_1-3>li:before{content:»» counter(lst-ctn-kix_list_1-3,decimal) «. «}#doc6977624 .lst-kix_list_1-0>li{counter-increment:lst-ctn-kix_list_1-0}#doc6977624 ol.lst-kix_list_2-7.start{counter-reset:lst-ctn-kix_list_2-7 0}#doc6977624 ol.lst-kix_list_2-1.start{counter-reset:lst-ctn-kix_list_2-1 0}#doc6977624 ol.lst-kix_list_1-3.start{counter-reset:lst-ctn-kix_list_1-3 0}#doc6977624 .lst-kix_list_1-3>li{counter-increment:lst-ctn-kix_list_1-3}#doc6977624 .lst-kix_list_2-7>li{counter-increment:lst-ctn-kix_list_2-7}#doc6977624 ol.lst-kix_list_2-6.start{counter-reset:lst-ctn-kix_list_2-6 0}#doc6977624 .lst-kix_list_1-2>li{counter-increment:lst-ctn-kix_list_1-2}#doc6977624 ol.lst-kix_list_2-5.start{counter-reset:lst-ctn-kix_list_2-5 0}#doc6977624 ol.lst-kix_list_1-7{list-style-type:none}#doc6977624 ol.lst-kix_list_1-8{list-style-type:none}#doc6977624 .lst-kix_list_1-6>li:before{content:»» counter(lst-ctn-kix_list_1-6,decimal) «. «}#doc6977624 .lst-kix_list_2-6>li:before{content:»» counter(lst-ctn-kix_list_2-6,decimal) «. «}#doc6977624 .lst-kix_list_1-4>li{counter-increment:lst-ctn-kix_list_1-4}#doc6977624 .lst-kix_list_2-2>li:before{content:»» counter(lst-ctn-kix_list_2-2,lower-roman) «. «}#doc6977624 .lst-kix_list_1-7>li:before{content:»» counter(lst-ctn-kix_list_1-7,lower-latin) «. «}#doc6977624 ol.lst-kix_list_1-8.start{counter-reset:lst-ctn-kix_list_1-8 0}#doc6977624 ol.lst-kix_list_1-4.start{counter-reset:lst-ctn-kix_list_1-4 0}#doc6977624 ol.lst-kix_list_1-2{list-style-type:none}#doc6977624 ol.lst-kix_list_1-1{list-style-type:none}#doc6977624 .lst-kix_list_2-1>li:before{content:»» counter(lst-ctn-kix_list_2-1,lower-latin) «. «}#doc6977624 ol.lst-kix_list_1-0{list-style-type:none}#doc6977624 .lst-kix_list_2-2>li{counter-increment:lst-ctn-kix_list_2-2}#doc6977624 ol.lst-kix_list_1-6{list-style-type:none}#doc6977624 ol.lst-kix_list_1-5{list-style-type:none}#doc6977624 ol.lst-kix_list_1-4{list-style-type:none}#doc6977624 ol.lst-kix_list_1-3{list-style-type:none}#doc6977624 ol{margin:0;padding:0}#doc6977624 .c10{border-bottom-width:1pt;border-top-style:solid;width:32.8pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c4{border-bottom-width:1pt;border-top-style:solid;width:35.3pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c19{border-bottom-width:1pt;border-top-style:solid;width:33.2pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c9{border-bottom-width:1pt;border-top-style:solid;width:30pt;border-right-style:solid;padding:0pt 5.4pt 0pt 5.4pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}#doc6977624 .c2{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;text-align:center;direction:ltr;padding-bottom:0pt}#doc6977624 .c1{line-height:1.0;padding-top:0pt;widows:2;orphans:2;text-align:left;direction:ltr;padding-bottom:0pt}#doc6977624 .c13{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:center;direction:ltr;padding-bottom:0pt}#doc6977624 .c12{line-height:1.5;padding-top:0pt;widows:2;orphans:2;text-align:justify;direction:ltr;padding-bottom:0pt}#doc6977624 .c3{line-height:1.0;padding-top:0pt;widows:2;orphans:2;height:11pt;direction:ltr;padding-bottom:0pt}#doc6977624 .c6{line-height:1.0;padding-top:0pt;widows:2;orphans:2;direction:ltr;padding-bottom:0pt}#doc6977624 .c26{vertical-align:sub;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c0{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c25{vertical-align:baseline;font-size:14pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c11{vertical-align:super;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c22{vertical-align:super;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c27{vertical-align:baseline;font-size:24pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c32{vertical-align:baseline;font-size:9pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c20{vertical-align:baseline;font-size:12pt;font-family:»Noto Symbol»;font-weight:normal}#doc6977624 .c28{vertical-align:sub;font-size:12pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c7{vertical-align:baseline;font-size:12pt;font-family:»Times New Roman»;font-weight:bold}#doc6977624 .c35{vertical-align:baseline;font-size:20pt;font-family:»Times New Roman»;font-weight:normal}#doc6977624 .c5{color:#000000;font-style:normal;text-decoration:none}#doc6977624 .c14{margin-right:auto;border-collapse:collapse;margin-left:54pt}#doc6977624 .c18{margin-right:auto;border-collapse:collapse;margin-left:-5.4pt}#doc6977624 .c15{padding-left:0pt;text-align:justify;margin-left:36pt}#doc6977624 .c33{max-width:786pt;background-color:#ffffff;padding:28.4pt 25.9pt 27pt 30pt}#doc6977624 .c36{padding-left:0pt;margin-left:36pt}#doc6977624 .c23{margin:0;padding:0}#doc6977624 .c17{text-indent:54pt;margin-left:-54pt}#doc6977624 .c29{text-align:justify}#doc6977624 .c8{height:0pt}#doc6977624 .c16{text-align:center}#doc6977624 .c21{height:11pt}#doc6977624 .c30{font-style:normal}#doc6977624 .c31{font-style:italic}#doc6977624 .c24{text-decoration:underline}#doc6977624 .c34{margin-left:18pt}#doc6977624 .title{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:36pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6977624 .subtitle{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#666666;font-style:italic;font-size:24pt;font-family:»Georgia»;padding-bottom:4pt;page-break-after:avoid}#doc6977624 li{color:#000000;font-size:11pt;font-family:»Arial»}#doc6977624 p{color:#000000;font-size:11pt;margin:0;font-family:»Arial»}#doc6977624 h2{widows:2;padding-top:24pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:24pt;font-family:»Arial»;font-weight:bold;padding-bottom:6pt;page-break-after:avoid}#doc6977624 h3{widows:2;padding-top:18pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:18pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6977624 h4{widows:2;padding-top:14pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:14pt;font-family:»Arial»;font-weight:bold;padding-bottom:4pt;page-break-after:avoid}#doc6977624 h5{widows:2;padding-top:12pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:12pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 h5{widows:2;padding-top:11pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:11pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 h6{widows:2;padding-top:10pt;line-height:1.15;orphans:2;text-align:left;color:#000000;font-size:10pt;font-family:»Arial»;font-weight:bold;padding-bottom:2pt;page-break-after:avoid}#doc6977624 ]]>Б-Толкай 2013
ГБОУ СОШ с.Большой-Толкай
Методическое пособие по теме
«Построение кусочно-заданных функций
Составила ученица 9 класса
Кизельбашева Валентина.
Понятие о кусочных функциях. На различных участках числовой прямой функция может быть задана разными формулами. Например: y=f(x), где
f(x)= х2, -3х-2
2х+8, -20
Такие функции назовём кусочными. Участки числовой прямой, которые различаются формулами задания, назовём составляющими область определения, а их объединение, является областью определения кусочной функции. Точки, которые делят область определения на составляющие, называются граничными точками. Выражения, определяющие кусочную функцию на каждой составляющей области определения, называется входящими функциями.
Наличие таких свойств как чётность, нечётность, нули функции, промежутки знакопостоянства, монотонность, ограниченность у кусочных функций устанавливается согласно общепринятым определениям, с учётом особенностей составляющих области определения и входящих функций.
Для того чтобы вычислить значение кусочной функции в заданной точке, необходимо, во-первых, определить, какой составляющей области определения принадлежит эта точка, а, во-вторых, найти значение входящей функции на этой составляющей.
Ответы:
1)Функция убывает на промежутке [-2; +∞).
2)Функция возрастает на промежутках (-∞; -2] и [0; 2].
3)f(x)≥0, если х=0 и |х|≥ 3⅓;
4)у > 0, если х
5)Прямая y=m имеет с графиком две общие точки при m=3 и m=-1;
6)Прямая y=m имеет с графиком одну общую точку при m=-2 и m>1.
Задания для самостоятельной работы:
1)Постройте график функции y=f(x), где
x-1, если х
f(x)=
-1/2x+3, если x ≥ -2.
Укажите промежуток, на котором функция убывает.
2)Постройте график функции у=f(x), где
1/4х2-1, если -2≤ х ≤ 2
f(x)= 2-х, если х > 2
х+2, если х
Укажите промежутки возрастания функции.
3)Постройте график функции у=f(x), где
-х2, если -2≤ х ≤ 2
f(x)= 3х-10, если х > 2
-3x-10, если х
При каких значениях х значения функции у= f(x) неотрицательны?
4)Постройте график функции у= f(x),где
(х+1)2, если х
f(x)=
1-х2, если х ≥0.
При каких значениях х выполняется неравенство у > 0?
5)Постройте график функции у= f(x),где
х2-4х-1, если х ≥ 4
f(x)=
-х2+4х-1, если х
При каких значениях m прямая y=m имеет с графиком этой функции две общие точки?
6)Постройте график функции у= f(x),где
4/х, если х ≤ -2
f(x)= х, если -2
х2-4х+4, если х > 1.
При каких значениях m прямая y=m имеет с графиком этой функции одну общую точку?
Чтобы построить график кусочной функции, нужно:
- Построить в одной системе координат графики входящих функций,
- Провести прямые x=a, x=a, x=a, где a-граничные точки,
- На каждой составляющей области определения (a, a), где i=1…n выбрать тот график, который соответствует входящей функции на этой составляющей.
- Выяснить значение функции в граничных точках.
Если каждая входящая кусочной функции является линейной, то будем называть её кусочно-линейной функцией.
f(x)= х2, -3х-2
2х+8, -20
Построение:
- у=х2
- -3х-2
- Выделить часть графика 1.
- У=2х+8
- -20
- Выделить часть графика 2.
Рассмотрим построение графиков кусочных функций.
Постройте график функции y=f(x), где
f(x)= -1/2х+3, если х2
х-4 ,х>2
Укажите промежуток, в котором функция убывает.
Построим в одной системе координат графики функций у=1/2х+3, если х2 и у=х-4 ,х>2
Графиками обеих функций являются прямые. Для построения достаточно двух точек.
у=1/2х+3, х2
х | 2 | 4 |
у | 2 | 1 |
у=х-4 ,х>2
Ответ: Функция убывает на промежутке (-;2]
Постройте график функции y=f(x), где
2-2×2, если 2
f(x)= x-1, если x>1
-x-1, если x
Укажите промежутки возрастания функции.
Первым графиком функции является парабола, ветви направлены вниз. Построим график функции на отрезке [-2;2]
Второй график у= х-1 –прямая.
Третий график тоже прямая у=-х-1
Ответ: Функция возрастает на промежутках[-1;0]
и [1;)
Постройте график функции у=f(x), где
х2-1, если х0
f(x)= (x-1)2 ,если х>0
При каких значениях х выполняется неравенство у0
1)Первым графиком является парабола. Построим её часть (х0) путем сдвига вниз на 1 графика у= х2.
Вторым графиком является тоже парабола. Построим её часть (х>0)путем сдвига вдоль оси ох вправо на 1 графика у= х2.
Ответ: при у>0, x1
Постройте график функции у=f(x), где
-х2-4х-3, если x-1
f(x)= x+1, если -11
2/x, если х>1
При каких значениях m прямая у=m имеет с графиком этой функции две общие точки.
Построим в одной системе координат графики функций.
1) Первым графиком функции является часть параболы, ветви направлены
вниз. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/(-1·2)=-2, то у=-(-2)2-4·(-2)-3=1.Итак, вершина параболы
в точке с координатой (-2;1).
Найдём точки пересечения с осью OX;
у=0. -х2-4х-3=0
х1=-3
х2=-1
Точки пересечения с осью OX: (-3;0) и (-1;0).
Найдём точки пересечения с осью Oу:
х=0
у=-(0)2-4·0-3=3
Точки пересечения с осью OX: (0;3).
Найдём дополнительные точки
2) Второй график у= х+1 –прямая.
Построим часть прямой
3)Третьим графиком является гипербола.
Построим часть гиперболы при х>1
Ответ: прямая у=m имеет с графиком этой функции две общие точкипри m=0 и 1
Постройте график функции у=f(x), где
f(x)= -х2, если |х|1
x2-1если |х| >1
Укажите промежутки возрастания функции.
Раскрывая знак модуля данную систему можно записать в следующем виде:
f(x)= -х2, если -1х1
x2-1если , х >1
x
Графиками данных функций является парабола. Построим первый график.
у=-х2 ,если -1х1
x2-1если , х >1
x
х | 1 | 2 | 3 | 4 | -1 | -2 | -3 | -4 |
у | 0 | 3 | 8 | 15 | 0 | 3 | 8 | 15 |
Ответ: функция возрастает на промежутках(- ;-1] и [0;1]
Постройте график функции у=f(x), где
х2-4х+4, если x>1
f(x)= x, если -21
4/x, если х-2
При каких значениях m прямая у=m имеет с графиком этой функции одну общую точку?
Построим в одной системе координат графики функций.
1) Первым графиком функции является часть параболы, ветви направлены
вверх. Найдём вершину параболы по формуле х=-b/2a
х=-(-4)/2·1=2
у=22-4·2+4=0
Итак, вершина параболы
в точке с координатой (2;0).
Найдём точки пересечения с осью OX;
у=0
х2-4х+4=(х-2)2 ; х=0
Точки пересечения с осью OX: (0;2).
Найдём точки пересечения с осью Oу: х=0
у=02-4·0+4=4
Точки пересечения с осью OX: (0;4).
Найдём дополнительные точки
2) Второй график у= х –прямая, проходящая через начало координат.
Часть прямой, находящийся в 1 и 3 четверти.
3)Третьим графиком у=4/x, является гипербола, которая находится в 3 четверти.
Построим часть гиперболы при х-2
Ответ: прямая у=m имеет с графиком одну общую точку при m=-2 и m>1
Постройте график функции у=. При каких значениях х выполняется неравенство у3?
Область определения данной функции D(у)=(-;0)(0;2) (2;+).
Разложим числитель и знаменатель на множители дроби вынесением общего множителя за скобки. Дальше числитель разложим на множители по формуле
ax2+bx+c=a(x-x1)(x-x2)
Преобразуем дробь: у====-х-1
у=-х-1-линейная функция, графиком является прямая, рисунок 1
рис.1
Для того , чтобы ответить на вопрос
рассмотрим рисунок 2
Рис.2
Ответ: неравенство у3 выполняется при
-4х2.
Найдите все значения к, при которых прямая у=кх пересекает в трёх точках ломанную, заданную условием:
2х+4, если х
у= -2, если-33
2х-8,если х>3
Прямая y= kx пересекает в трех
различных точках эту ломаную, если ее угловой
коэффициент больше углового коэффициента
прямой, проходящей через точку –(3; -2), и
меньше углового коэффициента прямой,
парал. прямым у=2х+4 ,у=2х-8 .
Найдем угловой коэффициент прямой,
проходящей через точку (-3;-2)
-2=-3к, к=2/3
Угловой коэффициент k прямой, парал.
Прямой у=2х+8 , равен 2.
Ответ: прямая имеет с ломанной три общие точки при 2/3
Построение кусочной функции / Geogebra в SMART Notebook / EdGuru.RU
Сегодня мы рассмотрим построение кусочных функций в режиме Алгебра и графики виджета Geogebra.Нам необходимо построить графики следующих функций:

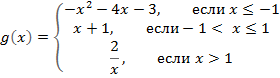
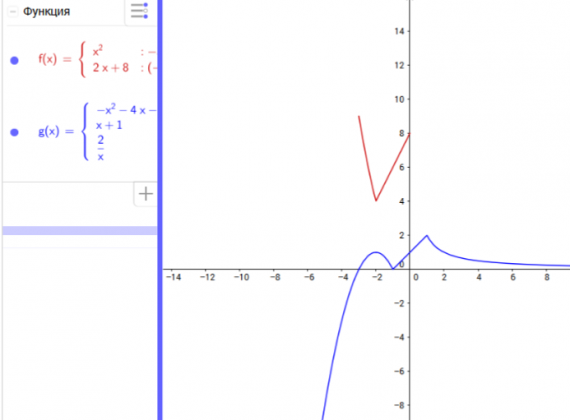
Способ 1.
Нажмите на знак плюса  в строке ввода Алгебраического вида, появится всплывающее меню с пунктами: Piecewise function, Матрица, Параметрическая кривая.
в строке ввода Алгебраического вида, появится всплывающее меню с пунктами: Piecewise function, Матрица, Параметрическая кривая.
Piecewise function – это и есть кусочная функция. Выбрав этот пункт, в окне алгебраического вида отобразится формула 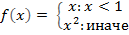
Исправьте содержимое формулы согласно заданию.
Подсказка: Для того, чтобы увеличить количество интервалов для задания кусочной функции, нажмите на знак +, расположенный рядом с кнопкой удаления объекта

Способ 2.
Другой способ задания кусочной функции — это ввод команды с условным оператором. Рассмотрим несколько примеров.
Команда function [ 2x-1, 0, 3 ] – задаст функцию 2x-1 на промежутке от 0 до 3. Таким образом, вы можете задавать каждый участок, но график не будет объединен в единое целое. Иногда так удобно делать, если вы хотите, например, окрасить различные части графика в разные цвета.
Команда f(x) = if [ x>=3, 2x-16 ] – задаст функцию 2x-16 на промежутке от (3;+∞).
Команда f(x) = if [ -1<x<3, x^2+1, x-1 ] – задаст функцию x2+1 на промежутке от -1 до 3, на всей остальной числовой прямой будет построен график функции x-1. Таким образом, синтаксис условного оператора:
if [ условие, если верно, иначе ]
В качестве параметра иначе может выступать еще один оператор условия.
Таким образом, для задания функции g(x) из задания требуется написать команду:
g(x) = if [ x<=-1, -x^2-4x-3, if [ -1<x<=1, x+1, 2/x ] ].
Как построить график кусочной функции
☰
Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,
Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x2. Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x2 (сначала возводим в квадрат, потом учитываем минус).
Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.
Для приведенного выше примера для формулы y = √x получим такой график:
Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.
Построим график функции f(x) = –x2. Получим перевернутую параболу:
В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:
Рассмотрим другой пример:
Графиком функции f(x) = (0.6x – 0.5)2 – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:
В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой:
Кусочные функции. Графики кусочно-линейных функций
Реальные процессы, происходящие в природе, можно описать с помощью функций. Так, можно выделить два основных типа течения процессов, противоположных друг другу – это постепенное или непрерывное и скачкообразное (примером может служить падение мяча и его отскок). Но если есть разрывные процессы, то существуют и специальные средства для их описания. С этой целью вводятся в обращение функции, имеющие разрывы, скачки, то есть на различных участках числовой прямой функция ведет себя по разным законам и, соответственно, задается разными формулами. Вводятся понятия точек разрыва, устранимого разрыва.
Наверняка вам уже встречались функции, заданные несколькими формулами, в зависимости от значений аргумента, например:
y = {x – 3, при x > -3;
{-(x – 3), при x
Такие функции называются кусочными или кусочно-заданными . Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками . Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями . Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.
Упражнения.
Построить графики кусочных функций:
1) {-3, при -4 ≤ x f(x) = {0, при x = 0,
{1, при 0
График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами (0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси Ох.
Ответ: рисунок 1.
2) {3, если x ≤ -4,
f(x) = {|x 2 – 4|x| + 3|, если -4 {3 – (x – 4) 2 , если x > 4.
Рассмотрим отдельно каждую функцию и построим ее график.
Так, f(x) = 3 – прямая, параллельная оси Ох, но изображать ее нужно только на участке, где x ≤ -4.
График функции f(x) = |x 2 – 4|x| + 3| может быть получен из параболы y = x 2 – 4x + 3. Построив ее график, часть рисунка, которая лежит над осью Ox, необходимо оставить без изменений, а часть, которая лежит под осью абсцисс, симметрично отобразить относительно оси Ox. Затем симметрично отобразить часть графика, где
x ≥ 0 относительно оси Oy для отрицательных x. Полученный в результате всех преобразований график оставляем только на участке от -4 до 4 по оси абсцисс.
График третьей функции – парабола, ветви которой направлены вниз, а вершина находится в точке с координатами (4; 3). Чертеж изображаем только на участке, где x > 4.
Ответ: рисунок 2.
3) {8 – (x + 6) 2 , если x ≤ -6,
f(x) = {|x 2 – 6|x| + 8|, если -6 ≤ x {3, если x ≥ 5.
Построение предлагаемой кусочной-заданной функции аналогично предыдущему пункту. Здесь графики первых двух функций получаются из преобразований параболы, а график третьей – прямая, параллельная Ох.
Ответ: рисунок 3. 
4) Построить график функции y = x – |x| + (x – 1 – |x|/x) 2 .
Решение. Область определения данной функции – все действительные числа, кроме нуля. Раскроем модуль. Для этого рассмотрим два случая:
1) При x > 0 получим y = x – x + (x – 1 – 1) 2 = (x – 2) 2 .
2) При x
Таким образом, перед нами кусочно-заданная функция:
y = {(x – 2) 2 , при x > 0;
{ x 2 + 2x, при x
Графики обоих функций – параболы, ветви которых направлены вверх.
Ответ: рисунок 4.
5) Построить график функции y = (x + |x|/x – 1) 2 .
Решение.
Легко видеть, что областью определения функции являются все действительные числа, кроме нуля. После раскрытия модуля получим кусочно-заданную функцию:
1) При x > 0 получим y = (x + 1 – 1) 2 = x 2 .
2) При x 
Перепишем.
y = {x 2 , при x > 0;
{(x – 2) 2 , при x
Графики этих функций – параболы.
Ответ: рисунок 5.
6) Существует ли функция, график которой на координатной плоскости имеет общую точку с любой прямой?
Решение.
Да, существует.
Примером может быть функция f(x) = x 3 . Действительно, с вертикальной прямой х = а график кубической параболы пересекается в точке (а; а 3). Пусть теперь прямая задана уравнением y = kx + b. Тогда уравнение
x 3 – kx – b = 0 имеет действительный корень х 0 (так как многочлен нечетной степени всегда имеет хотя бы один действительный корень). Следовательно, график функции пересекается с прямой y = kx + b, например, в точке (х 0 ; х 0 3).
сайт, при полном или частичном копировании материала ссылка на перво
Построение кусочной функции — манекены
- Образование
- Математика
- Алгебра
- Построение кусочной функции
Мэри Джейн Стерлинг
Кусочная функция состоит из двух или более функциональных правил (функциональных уравнений), соединенных вместе (перечисленных отдельно для разных значений x ), чтобы сформировать одну большую функцию.
Изменение уравнения функции происходит для разных значений в области.Например, у вас может быть одно правило для всех отрицательных чисел, другое правило для чисел больше трех и третье правило для всех чисел между этими двумя правилами.
Кусочные функции находят свое место в ситуациях, когда вы не хотите использовать одно и то же правило для всех или для всего. Должен ли ресторан взимать с 3-летнего ребенка столько же, сколько и со взрослого? Вы надеваете такое же количество одежды при температуре 20 градусов, как и в более жаркую погоду? Нет, вы устанавливаете разные правила для разных ситуаций.В математике кусочная функция позволяет применять разные правила к разным числам в области определения функции.
Ниже приведен пример кусочной функции:
С помощью этой функции вы используете одно правило для всех чисел, меньших или равных –2, другое правило для чисел от –2 до 3 (включая 3) и последнее правило для чисел больше 3. У вас остается только одно правило. выходное значение для каждого входного значения. Например, предположим, что вы хотите найти значения этой функции для x , равные –4, –2, –1, 0, 1, 3 и 5.Обратите внимание, как вы используете разные правила в зависимости от входного значения:
На рисунке показан график кусочной функции с этими значениями функции.
На графике кусочных функций отображаются как связи, так и пробелы.
Обратите внимание на три разных участка графика. Левая кривая и средняя линия не соединяются, потому что существует разрыв, когда x = –2. Разрыв возникает, когда на графике появляется разрыв или дыра. Также обратите внимание, что левая линия, падающая к оси x , заканчивается сплошной точкой, а в средней части есть открытый кружок прямо над ней.Эти функции сохраняют определение функции — только один выход для каждого входа. Точка говорит вам использовать правило слева, когда x = –2.
Средняя секция соединяется в точке (3, 2), потому что правило справа действительно очень близко к тому же выходному значению, что и правило в середине, когда x = 3. Технически вы должны нарисовать оба полых круга. и точка, но вы действительно не сможете определить эту особенность, просто взглянув на нее.
.кусочных функций
Функция может быть в частях
Мы можем создавать функции, которые ведут себя по-разному в зависимости от значения input (x).
Функция из 3 частей
Пример:
- , когда x меньше 2, дает x 2 ,
- , когда x равно 2, дает 6
- , когда x больше 2 и меньше или равно 6, получается строка 10-x
Это выглядит так:
(сплошная точка означает «включая»,
открытая точка означает «не включая»)
А вот как мы это пишем:
Домен (все значения, которые могут входить в функцию) — это все действительные числа до 6 включительно, которые мы можем записать так:
Dom (f) = (-∞, 6] (с использованием обозначения интервалов)
Dom (f) = {x | x ≤ 6} (с использованием нотации Set Builder)
А вот несколько примеров значений:
| Х | Я |
|---|---|
| −4 | 16 |
| -2 | 4 |
| 0 | 0 |
| 1 | 1 |
| 2 | 6 |
| 3 | 7 |
Пример: вот еще одна кусочная функция:
| , который выглядит так: |
Что такое h (−1)?
x ≤ 1, поэтому мы используем h (x) = 2, поэтому h (−1) = 2
Что такое h (1)?
x ≤ 1, поэтому мы используем h (x) = 2, поэтому h (1) = 2
Что такое h (4)?
x> 1, поэтому мы используем h (x) = x, поэтому h (4) = 4
Кусочные функции позволяют создавать функции, которые делают все, что мы хотим!
Пример: Гонорар врача зависит от продолжительности времени.
- До 6 минут стоит 50 долларов
- От 6 до 15 минут стоит 80 долларов
- Более 15 минут стоит 80 долларов плюс 5 долларов за минуту свыше 15 минут
Что мы можем написать так:
Вы приходите на 12 минут, сколько стоит? $ 80
Вы приходите на 20 минут, сколько стоит? 80 $ + 5 $ (20-15) = 105 9000 $ 5
Функция абсолютного значения
Функция абсолютного значения — известная кусочная функция.
состоит из двух частей:
- ниже нуля: -x
- начиная с 0: x
f (x) = | x |
Функция этажа
Функция Floor — это особая кусочная функция. В нем бесконечное количество штук:
Функция этажа
.Графики кусочных функций
Я изучаю кусочные функции и не могу понять, как использовать эту функцию в GeoGebra. Например, в моей школе есть список инструкций, но для меня это не имеет смысла. Вот функции и инструкции.
f (x) = | x + 5 | — 4, если x <-5
f (x) = -1 / 5X, если -5 ≤ x <0
f (x) = (SQRTx) +3, если 0 ≤ x <4
f (x) = -x ^ 2 + 8x — 10, если x ≥ 4
Рядом с каждым общим описанием для построения графика кусочной функции с помощью Geogebra есть специальный текст для этой проблемы, который выделен жирным шрифтом.Специальные символы, такие как больше или равно (≥), меньше или равно (≤), квадратный корень (квадратный корень) и столбцы абсолютных значений (| |), находятся в раскрывающемся списке рядом с полем ввода.
Снимок экрана панели инструментов ввода Geogebra со стрелкой, указывающей на раскрывающееся поле.
1. В поле ввода введите f (x) = If [
2. Введите условия первой функции и запятую. x <-5,
3. Введите выражение первой функции и запятую.abs (x + 5) — 4,
4. Введите If [
5. Введите условия второй функции и запятую. -5 ≤ x && x <0,
Примечание: Когда x ограничен с двух сторон, как в этом примере, -5 ≤ x <0, условия функции должны быть записаны отдельно с двумя знаками амперсанда && между ними. В противном случае GeoGebra не распознает команду.
6. Введите выражение второй функции и запятую. — (1/5) х,
7.2 + 8x — 10
13. Введите четыре закрытых скобки:]]]] и нажмите
14. В поле ввода введите каждую упорядоченную пару конечных точек отдельно.
15. Щелкните правой кнопкой мыши одну из точек, которая должна быть открытым кружком, и перейдите в «Свойства объекта». Измените стиль точек для точек, которые должны быть представлены открытыми кружками. Измените метку каждой точки на «Значение».
.