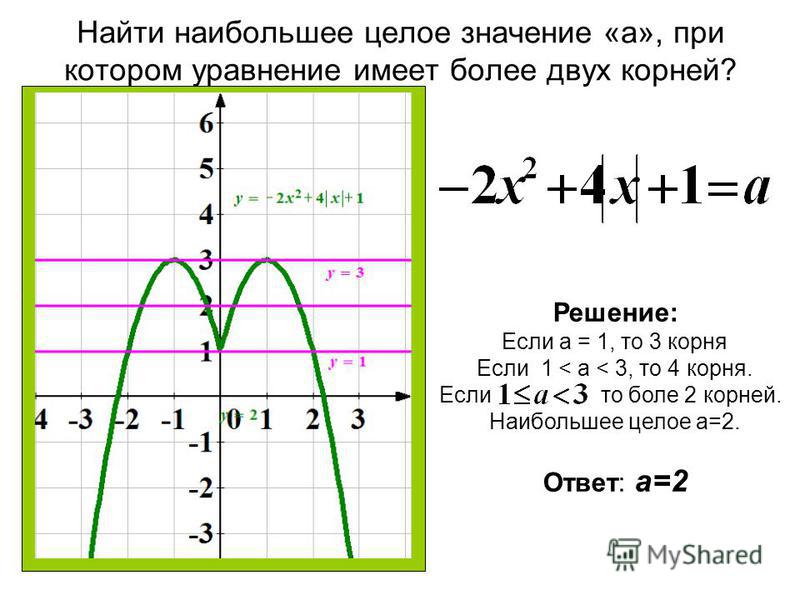
График функции с модулем | Алгебра
Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.
Рассмотрим примеры таких заданий.
1) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
Решение:
Область определения функции D(y): x∈R.
1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
x-2=0, x=2.
Найдём значение функции при x=2.
y(2)=5·0-2²+5∙2-3∙0-6=0.
Получили точку (2;0).
2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.
Если x-2>0, то есть при x>2, |х-2|=x-2,
y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.
y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).
Координаты вершины параболы
то есть вершина параболы — точка (5;9).
3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.
Если x-2<0, то есть при x<2, |х-2|=-(x-2),
y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.
y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.
Координаты вершины параболы
то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².
Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:
График функции с модулем можно рассматривать и как график кусочной функции:
Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:
Ответ: 0; 4.
2) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.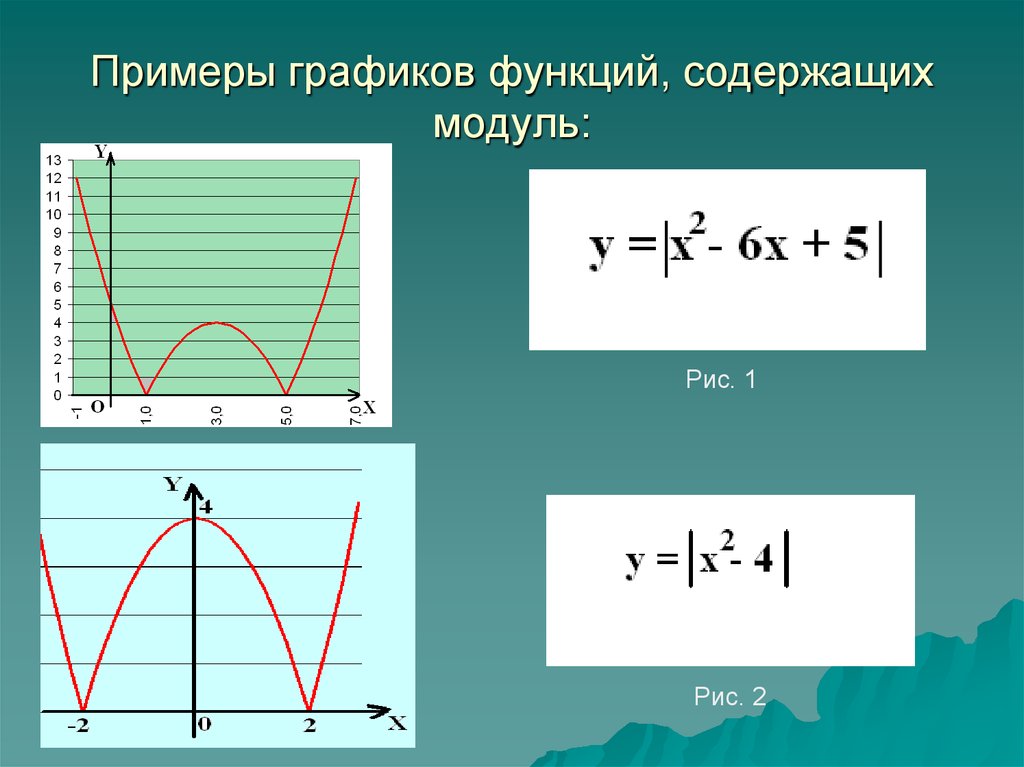
Решение:
Область определения функции D(y): x∈R.
1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:
|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.
y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).
Координаты вершины параболы
Так как a=1, от вершины (3;-10) строим график y=x².
|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.
y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.
Координаты вершины параболы
от вершины (-3;-8) строим график y=x².
Или:
Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:
Ответ: -8; 1/36.
3) Постройте график функции
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x=0, y=|0|·0+3·|0|-5·0=0.
2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.
y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).
Координаты вершины параболы
От вершины (1;-1) строим параболу y=x² (так как a=1).
3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.
y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).
Координаты вершины параболы
От вершины (-4;16) строим параболу y=-x² (так как a=-1).
Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:
Альтернативный вариант:
Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:
Ответ: -1; 16.
4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Решение:
Область определения функции D(y): x∈R.
Построим график функции y=x²+2x-3.
Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.
Координаты вершины параболы
, то есть вершина параболы — точка (-1;-4).
От вершины строим график функции y=x²:
График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.
Или y=|x²+2x-3|
Вершина параболы (-1;-4) при этом переходит в точку (-1;4):
Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).
Ответ: 4.
Рубрика: ОГЭ задание 22 | КомментарииУрок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»
“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”
Изучение квадратичной функции с модулем позволяет углубить знания учащихся в преобразовании графиков квадратичной функции. Учащиеся с большим интересом выполняют любые задания с модулем. Рассмотренные приемы построения графиков функции являются общими и применяются не только к квадратичной, но и к другим функциям.
I. Вводное слово учителя
Функция – одно из основных математических и
общенаучных понятий, выражающее зависимость
между переменными величинами. Математика
рассматривает абстрактные переменные величины,
изучает законы их взаимосвязи, не углубляясь в
природу задачи.
Например, в соотношении Y = Х2 математик
или геодезист увидит зависимость площади
квадрата от его стороны, а физик, авиаконструктор
или кораблестроитель может увидеть зависимость
силы Y сопротивления воздуха или воды от скорости
Х движения.
Математика же изучает эту зависимость в отвлеченном виде, и она устанавливает, например, что увеличение Х в 2 раза приведет к увеличению Y в 4 раза, и это заключение может применяться в любой конкретной ситуации.
Модуль и квадратичная функция
Построение графиков функций:
- Y = АХ2 + ВX + C,
- Y = АХ2 + ВX + C ,
- Y = АХ2 + ВХ + С
II. Устная работа
1) Дать определение модуля числа Х
2) Дать определение квадратичной функции,
рассказать все, что известно об этой функции
(график, свойства).
3) Найти на рисунке график функции Y = –Х2 + 4Х – 3.
4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?
5) Вспомнить, как построить график функции Y = Х
По определению модуля
График функции Y = Х симметричен относительно оси У.
III. Построение графиков функций:
Y = АХ2 + ВX + C,
Y = АХ2 + ВX + C,
Y = АХ2 + ВХ + С
Работа проводится в группах, т.к. графики в К–1
в) и К–3 в) одинаковы, их необходимо сравнить и
сделать вывод (всего 3 группы). Каждой группе
выдается карточка, в ней 3 задания. Учащиеся
должны построить графики квадратичной функции,
содержащей модуль, используя определение модуля
и сделать вывод: как построить график данной
функции, используя график квадратичной функции и
симметрию относительно осей координат.
Работа в группах.
а) определение модуля;
б) график функции Y = АХ2 + ВХ + С;
в) симметрию относительно осей координат.
а) Y = Х2 – 4 Х + 3
б) Y = Х2 – 4 Х + 3
в) Y = Х2 – 4 Х + 3
а) Y = Х2 + 2 Х – 3
б) Y = Х2 + 2 Х – 3
в) Y = Х2 + 2 Х – 3
а) Y = –Х2 + 4 Х – 3
б) Y = –Х2 + 4 Х – 3
в) Y = –Х2 + 4 Х – 3
IV. Учащиеся делают вывод о расположении графиков указанных функций
Вопрос: а) Как построить график функции Y = f (X)?
(1 способ.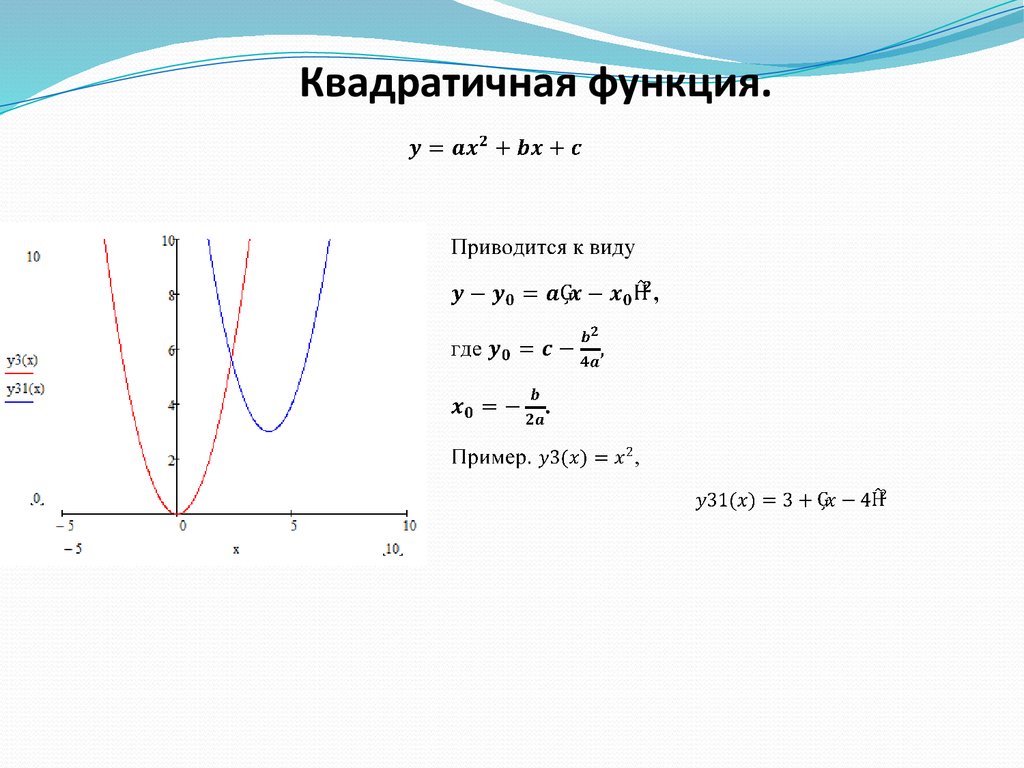
2 способ. Построить график функции Y = f (X) и отобразить правую часть графика симметрично относительно оси Y).
б) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).
в) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)
г) Почему графики функций Y = –Х2 + 4X – 3 и Y = Х2 – 4X + 3 одинаковы?
(Так как А = А , –А = А)
V.
У рассмотренных функций под знаком модуля была
независимая переменная. Теперь рассмотрим
функции, где под знаком модуля стоит либо сама
функция, либо и функция, и независимая переменная
одновременно, т.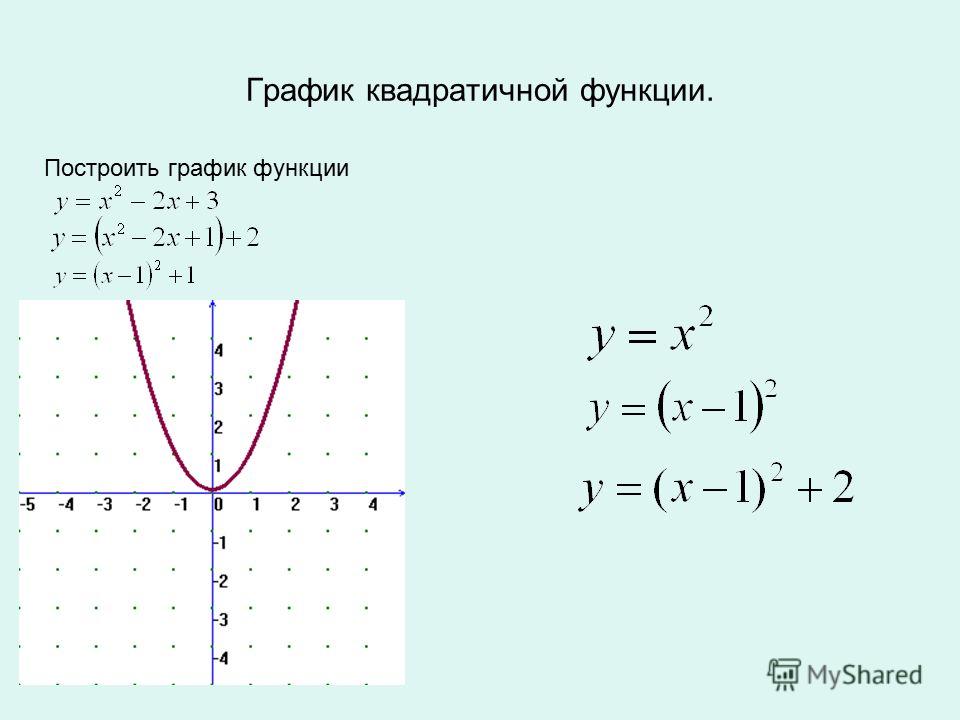
Y = АХ2 + ВX+ C и Y = АХ2 + ВX + C
Приведем конкретные примеры.
а) Y = Х2 – 4X+ 3
По определению
Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х2 – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.
б) Y = Х2 – 4X+ 3
Сначала строим график функции Y = Х2 – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х2 – 4X+ 3 , т.е. график функции Y = Х2 – 4X+ 3 отображаем относительно оси Х.
VI. Творческое задание
Дана функция Y = Х2 + 2X– 3
Выполнить всевозможные преобразования данной квадратичной функции с модулем.
Повторение абсолютных и квадратичных графиков
Прямые линииРадикалы и т.
д.
Purplemath
Очевидно, рисовать прямые линии будет проще всего. Но большую часть времени вы будете строить графики для уравнений, которые, по крайней мере, немного сложнее. Первый шаг вверх — это графики абсолютных значений, которые состоят (по крайней мере, когда вы начинаете) из двух прямых линий, образующих своего рода букву «V», либо с правой, либо с обратной стороны.
Содержание продолжается ниже. пример контекста, в котором мы должны быть осторожны, чтобы не забыть выбрать отрицательные значения x для нашей T-диаграммы. В противном случае очень легко забыть, что график абсолютного значения не будет просто одной непрерывной прямой линией.
Например, предположим, что нам дано уравнение y = | x |. И предположим, что мы выбрали только положительные значения x , поэтому наша Т-диаграмма выглядит так:
Тогда наши точки выглядят так:
И мы соединим наши точки так:
Мы только что завалили тест.
Вместо этого давайте немного разнесем наши значения x и не забудем на этот раз построить отрицательное значение x или два. Наша новая Т-диаграмма выглядит так:
Тогда наши точки выглядят следующим образом:
Поскольку наши точки хорошо разбросаны, и поскольку мы не забыли включить пару «минусовых» x -значений, мы помним, что уравнения абсолютных значений отображаются в виде ломаных линий, поэтому прикладываем нашу линейку дважды, чтобы получилось:
А это и есть правильный график!
(Если вы хотите изучить эту тему более подробно, см. Графики функций абсолютного значения.)
Квадратики
При графическом отображении квадратных уравнений/функций нам нужно нанести не только три точки; Я бы предложил минимум не менее пяти баллов, но от семи до девяти баллов будет лучше, если вы только начинаете. И мы должны ожидать, что нам также потребуется отображать отрицательные значения x .
Три точки больше не будут сокращать его, потому что квадратичные графики представляют собой кривые линии, называемые «параболами».
Например, предположим, что они дают нам y = x 2 − 6 x + 5. Есть множество вещей, которые мы можем сделать, чтобы помочь себе построить правильный график. Мы можем начать с поиска точек пересечения x и y . (Дополнительную информацию см. в разделе Перехваты.) В этом случае перехваты находятся в точках (1, 0), (5, 0) и (0, 5).
Кроме того, мы можем найти вершину параболы, которая является самой высокой или самой низкой точкой на графике. (Дополнительную информацию см. в разделе Вершина.) В этом случае вершина — это самая нижняя точка на графике, и эта точка находится в точке (3, −4).
Но в основном нам нужно потратить время, чтобы нанести довольно много точек, чтобы мы могли «увидеть» форму, прежде чем начать ее рисовать. Посмотрите, что часто происходит, когда новичок наносит только три точки:
T-диаграмма
Неправильный график
Но приведенный выше график неверен; эта парабола должна выглядеть как «смайлик», а не как прямая линия.
(И, если вы внимательно посмотрите, нанесенные точки на самом деле даже не выстраиваются в прямую линию! Линейка провела линию как бы «между» точками, а не «сквозь» их.)
Итак, нам нужно нанести еще несколько точек. Мы уже нашли точки пересечения и вершину (выше). Добавим к этому еще один пункт, используя x = 6:
Т-диаграмма
Правильный график
Гораздо лучше! Это график, который получит полные баллы!
(Примечание: положительное квадратичное выражение можно рассматривать как графическое изображение «смайлика», а отрицательное квадратичное выражение можно рассматривать как графическое изображение «фрони». Да, это глупый способ выразить это, но вы победите) Забудьте об этом сейчас, хорошо? Если вы хотите изучить эту тему более подробно, пожалуйста, обратитесь к разделу Графики квадратичных функций.)
URL: https://www.purplemath.com/modules/graphing2.htm
Page 1Page 3
8.3: Графики основных абсолютных значений и квадратичных функций
Раздел 8.
3 Задачи обучения8.31 и квадратичные функции
- Графические базовые функции абсолютного значения
- График основных квадратичных функций
В главе 2 мы рассмотрели идею абсолютного значения и представили стратегии решения уравнений и неравенств с абсолютными значениями. В этом разделе наша цель — построить график функций абсолютного значения.
Начнем с самой простой функции абсолютного значения, [latex]f(x)=|x|.[/latex]
Напомним, что абсолютное значение числа — это его расстояние от нуля на числовой прямой. Как и в случае с любой функцией, мы можем использовать таблицу, чтобы помочь нам в построении графика.
Поскольку мы не уверены в форме, мы хотим выбрать несколько точек, включая положительные и отрицательные стороны. Это приводит к таблице, приведенной ниже.
| [латекс]х[/латекс] | [латекс]f(x)=|x|[/латекс] |
| [латекс]-3[/латекс] | [латекс]|-3|=3[/латекс] |
| [латекс]-2[/латекс] | [латекс]|-2|=2[/латекс] |
| [латекс]-1[/латекс] | [латекс]|-1|=1[/латекс] |
| [латекс]0[/латекс] | [латекс]|0|=0[/латекс] |
| [латекс]1[/латекс] | [латекс]|1|=1[/латекс] |
| [латекс]2[/латекс] | [латекс]|2|=2[/латекс] |
| [латекс]3[/латекс] | [латекс]|3|=3[/латекс] |
Далее наносим точки.
Если бы мы не выбрали достаточное количество точек, у нас может возникнуть соблазн нарисовать что-то более похожее на гладкую кривую через точки. Однако мы видим, что для этого потребуется более линейный график, за исключением того, что он, кажется, внезапно меняет направление в начале координат. Если бы мы выбрали только точки справа от 0, мы могли бы подумать, что график будет представлять собой простую прямую линию, а не форму буквы «V», которая в конечном итоге выглядит так. Окончательный график [latex]f(x)=|x|[/latex] показан ниже.
Эта форма «V» будет появляться во всех простых функциях абсолютного значения, которые мы рассмотрим в этом разделе. Однако букву «V» можно сместить, сделать уже или шире или даже перевернуть.
График функций абсолютного значения вида [latex]f(x)=a|x|+b[/latex]
Знание основной формы графика абсолютного значения поможет нам в дальнейшем изучении абсолютных значений.
Рассмотрим функцию [latex]f(x)=|x|-3[/latex].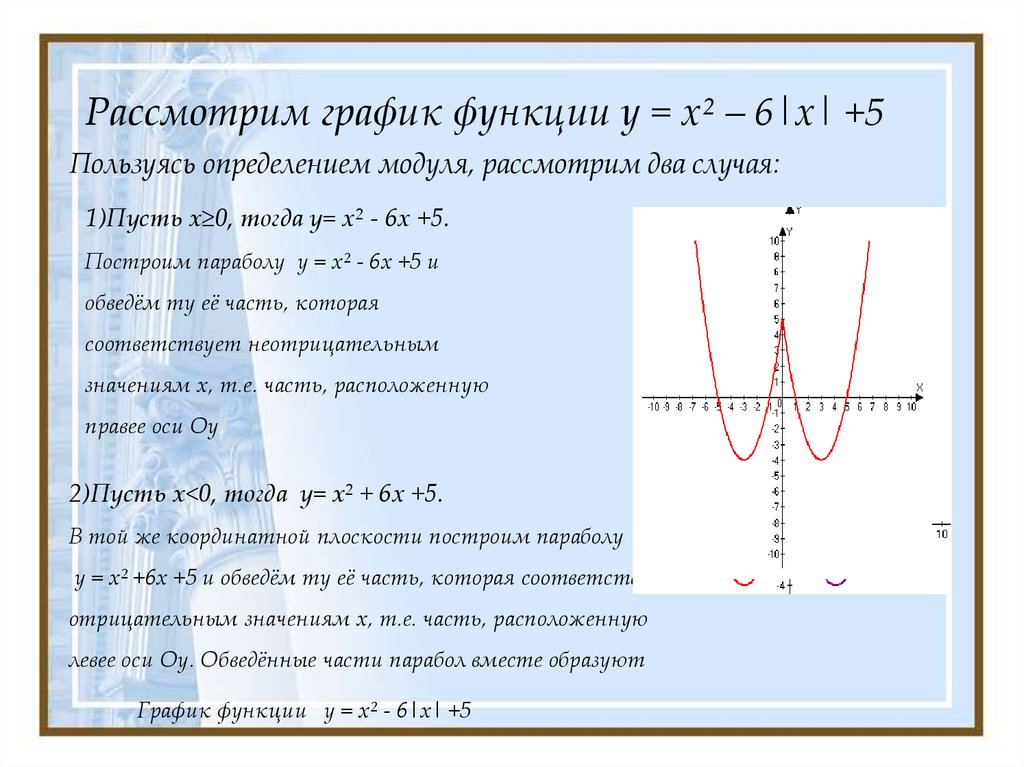
Давайте попробуем подставить те же значения для [latex]x[/latex], которые мы используем для базовой функции абсолютного значения.
| [латекс]x[/латекс] | [латекс]f(x)=|x|-3[/латекс] |
| [латекс]-3[/латекс] | [латекс]|-3|-3=3-3=0[/латекс] |
| [латекс]-2[/латекс] | [латекс]|-2|-3=2-3=-1[/латекс] |
| [латекс]-1[/латекс] | [латекс]|-1|-3=1-3=-2[/латекс] |
| [латекс]0[/латекс] | [латекс]|0|-3=0-3=-3[/латекс] |
| [латекс]1[/латекс] | [латекс]|1|-3=1-3=-2[/латекс] |
| [латекс]2[/латекс] | [латекс]|2|-3=2-3=-1[/латекс] |
| [латекс]3[/латекс] | [латекс]|3|-3=3-3=0[/латекс] |
Нанесение этих точек на график дает показанный ниже график.
Мы видим ту же форму буквы «V», которую мы ожидаем от этого типа функции абсолютного значения.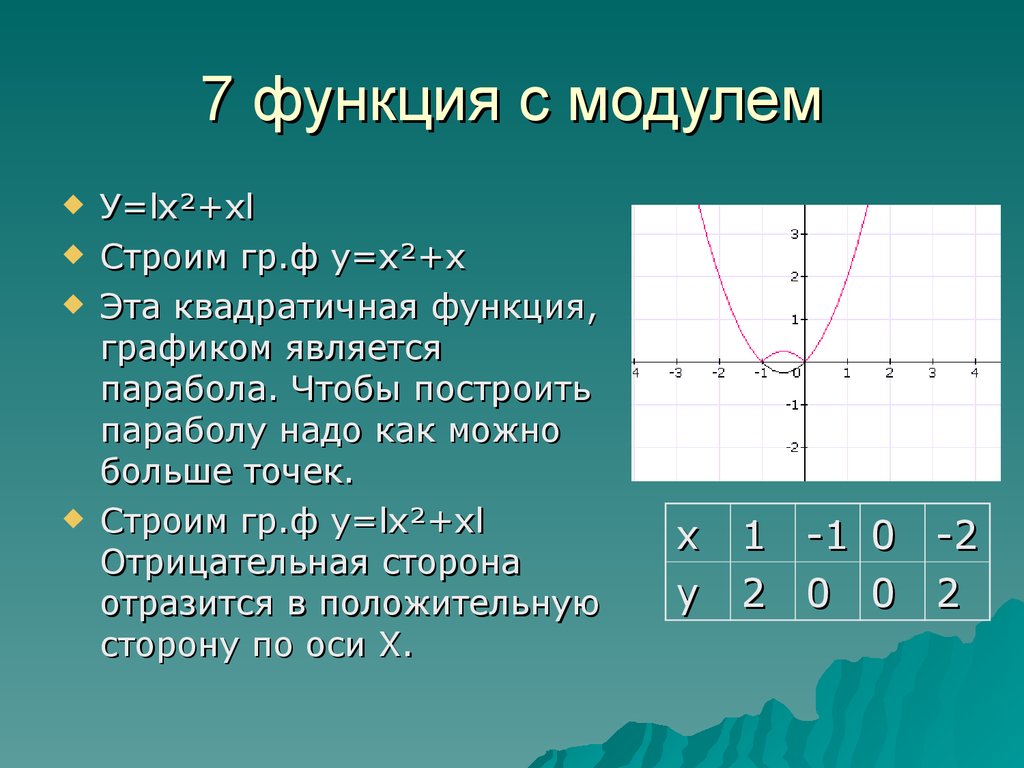
Однако не случайно обратите внимание, что кривая сместилась на 3 единицы вниз.
Пример 1
График [латекс]f(x)=|x|+2[/латекс].
Показать решение
Стратегия построения графиков функций абсолютного значения вида [latex]f(x)=a|x|+b[/latex]
- Создайте [latex]xy[/latex]-таблицу. Мы рекомендуем (как минимум) пять значений для [latex]x[/latex], [latex]x=-2,-1,0,1,2[/latex].
- График. Полученная кривая должна иметь форму буквы «V».
В следующей задаче мы увидим, что происходит, когда перед абсолютным значением стоит коэффициент, отличный от 1.
Пример 2
График [латекс]f(x)=2|x|[/латекс].
Показать решение
В нашем последнем примере мы комбинируем некоторые идеи, которые видели. Кроме того, мы смотрим на влияние отрицательного коэффициента.
Пример 3
График [латекс]f(x)=-2|x|+1[/латекс].
Показать решение
Если вы хотите подробнее изучить графики абсолютных значений, ознакомьтесь с приведенным ниже разделом «Думай об этом».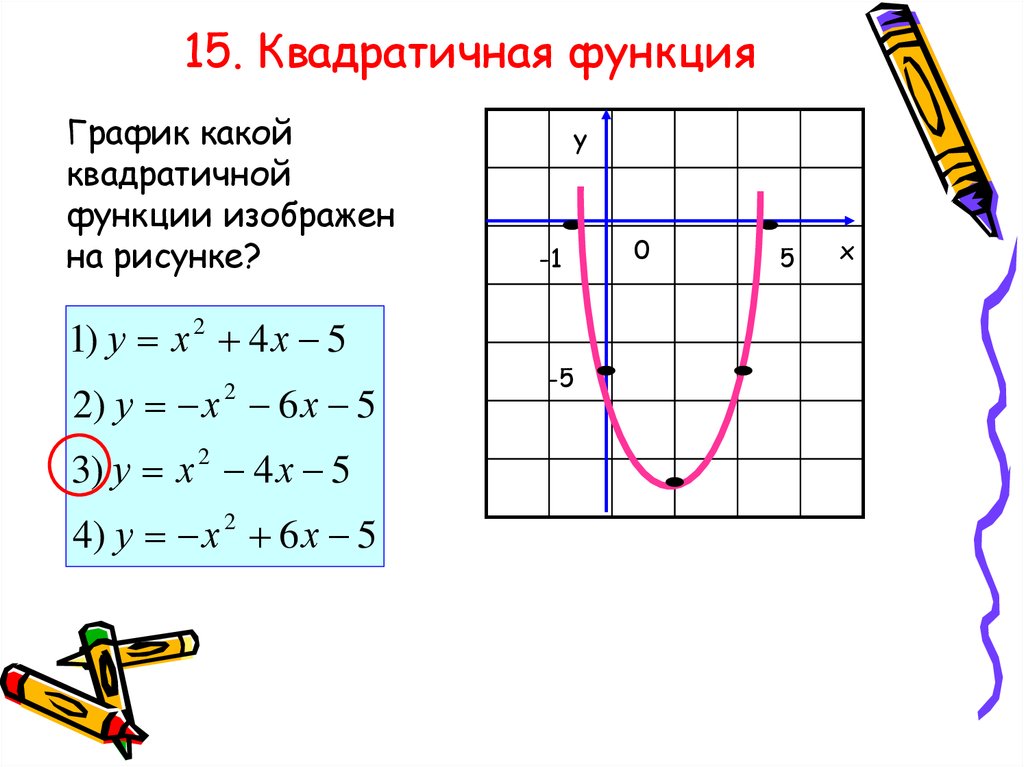
{2}[/latex]. 92=4[/латекс]
Теперь нанесем точки [латекс](-2,4), (-1,1), (0,0), (1,1), (2,4)[/латекс]
На первый взгляд может показаться, что эти точки образуют букву «V», как функции абсолютного значения, которые мы построили ранее. Но квадратичное семейство функций не рисуется прямыми линиями. Поскольку точек на линии , а не , вы не можете использовать линейку . Соедините точки как можно лучше, используя плавную кривую (не ряд прямых). Вы можете найти и нанести дополнительные точки (например, выделенные синим цветом ниже). Размещение стрелок на концах линий означает, что они продолжаются в этом направлении навсегда.
Обратите внимание, что форма похожа на букву U. Это называется параболой . Половина параболы является зеркальным отражением другой половины. Нижняя точка на этом графе называется вершиной . Вертикальная линия, проходящая через вершину, называется 9.{2}+c[/latex] выполните следующие действия:
- Распознайте форму квадратичной функции и то, что это будет парабола с центром вокруг точки x=0.
