Создатель графиков логарифмических функций — MathCracker.com
Алгебра Решатели
Инструкции: Этот создатель графика логарифмической функции позволяет вам построить логарифмическую функцию или сравнить график двух логарифмических функций. Вам необходимо предоставить базу \(b\) каждой из функций \(f(x) = \log_b x\).
Базовая функция 1 (Пример 10, 2, e и т.
Базовая функция 2 (Пример 10, 2, e и т. Д.) =
Баллы для оценки (необязательно. Запятая или пробел) =
Этот конструктор графиков позволяет отображать две логарифмические функции и, при желании, оценивать две функции при нескольких значениях.
С помощью этого калькулятора можно изобразить следующие логарифмические функции:
\[f(x) = \log_b x\]
Итак, чтобы получить соответствующие графики, вам просто нужно указать базы.
Что такое обратная логарифмическая функция и как ее построить?
Обратные логарифмические функции:
экспоненциальные функции
.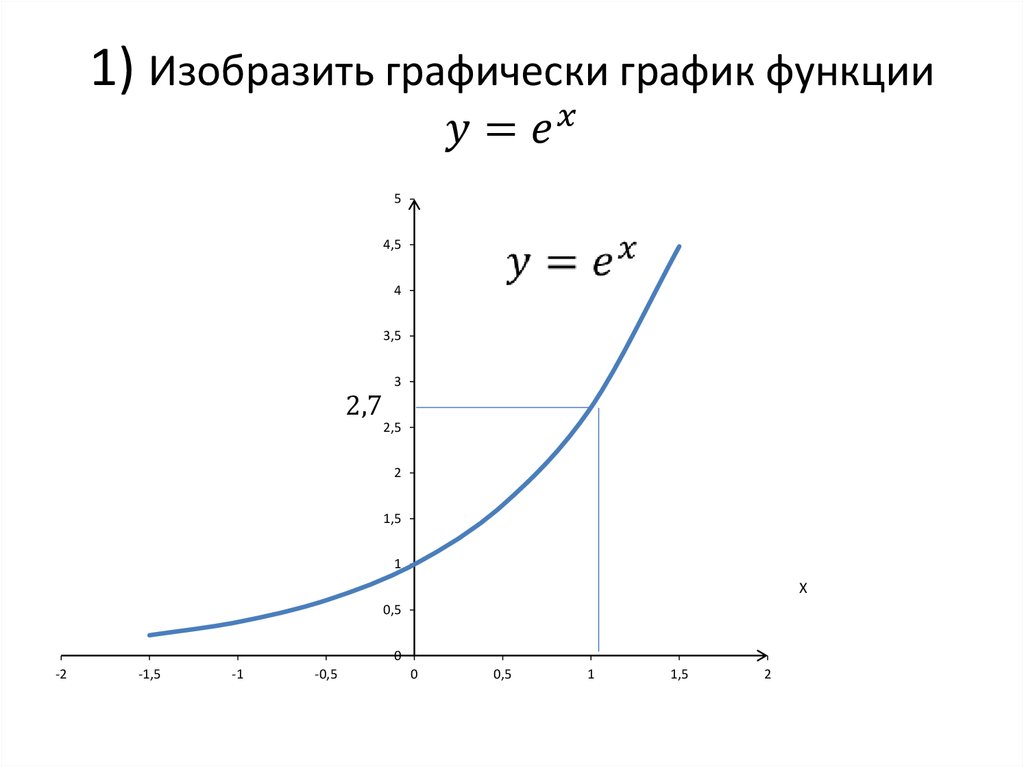 x\).
x\).
С точки зрения их графиков, график лог-функции и соответствующая экспоненциальная обратная функция симметричны относительно 45 O прямая линия.
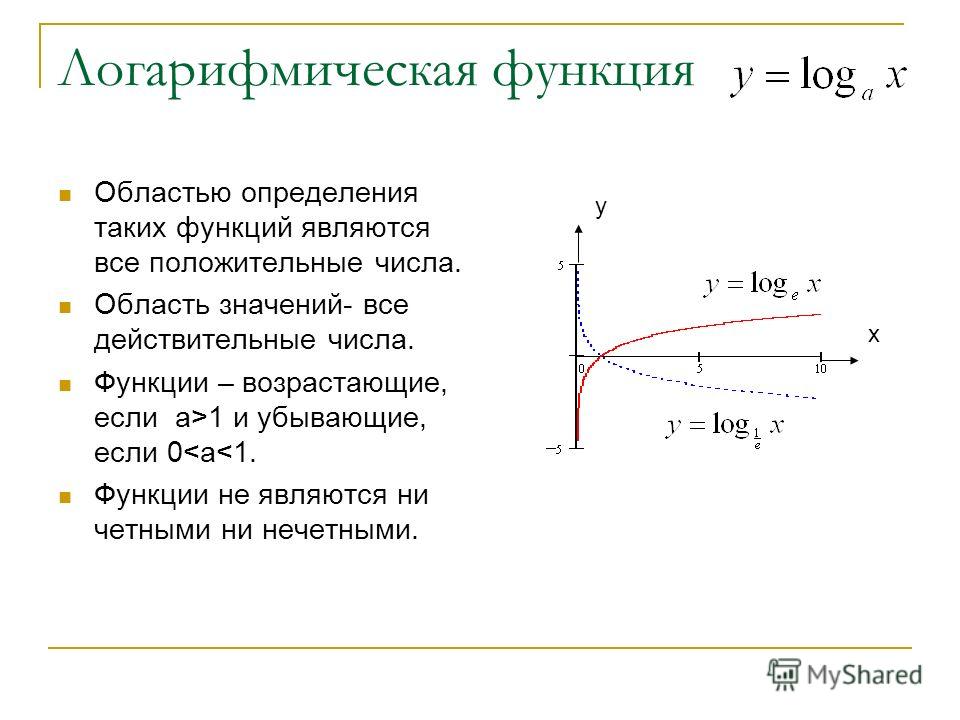
Как построить график экспоненциальной функции
Экспоненциальная функция указанной выше формы будет иметь характерную экспоненциальную форму, и ее общий вид будет зависеть от того, является ли коэффициент \(r\) положительным или отрицательным.
Для положительной ставки \(r\) будем иметь
экспоненциальный рост
, а при отрицательной ставке \(r\) будет
экспоненциальный спад
.
Какая польза от логарифмической бумаги?
Логарифмическая бумага — это особый тип бумаги, в которой масштаб изменен так, что теперь логарифмические функции отображаются в виде линейных функций. У них было свое время, в настоящее время графические устройства (подобные этому) легко доступны и делают логарифмическую бумагу довольно устаревшей.
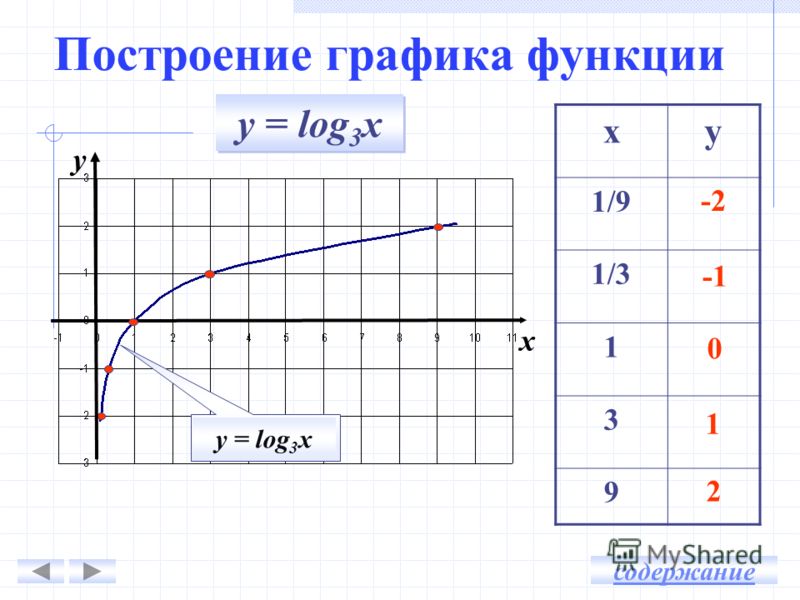
Как вы оцениваете логарифмическую функцию?
Часто бывает необходимо оценить
логарифмическая функция для прохождения двух точек
, и для этой цели вам дадут две точки, и вы решите систему для оценки требуемых параметров, чтобы логарифмическая функция проходила через эти точки.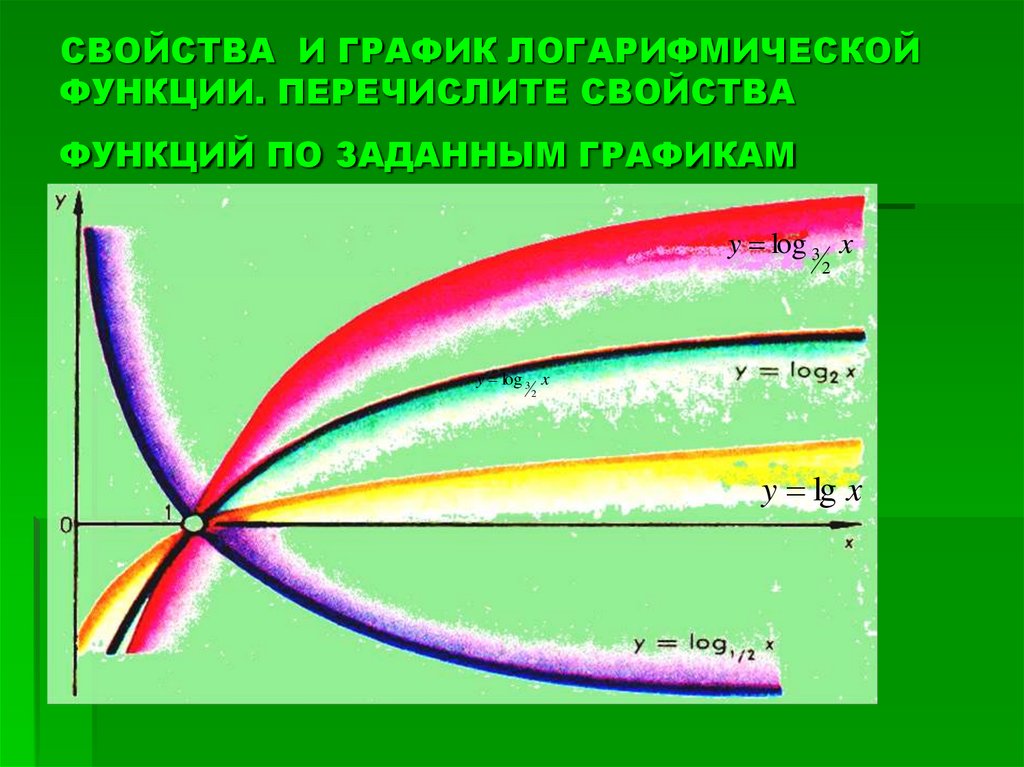
Калькулятор алгебры Алгебра Решатель Базовый пакет алгебры Создатель графиков Создатель графиков функций логарифма Создатель графиков логарифмических функций
Производные логарифмов и логарифмическое дифференцирование
- Как находить производные сложных логарифмических функций?
- Что такое логарифмическое дифференцирование?
- Найти производную логарифмической функции самостоятельно, а затем помотреть решение
Что можно сказать о производной логарифмической функции y = lnx на основании таблицы производных? Можно сказать, что она существует и выражается формулой
(1)
Однако в большинстве задач математического анализа, с которыми придётся столкнуться в дальнейшем,
присутствует сложная логарифмическая функция.
В случае сложной логарифмической функции y = lnu, где u – дифференцируемая функция аргумента x, формула (1) примет вид
(2)
Пользуясь формулой (2), найдём производную логарифмической функции с произвольным положительным основанием a. Пусть
В результате применения свойств логарифмов:
Так как — постоянный множитель, то
или
(3)
Пример 1. Найти производную функции
Решение. Применяя правило дифференцирования дроби (частного), а затем формулу (3), получим
Пример 2. Найти производную функции
Решение. Используя свойства логарифмов, данную функцию можно записать проще:
Используя свойства логарифмов, данную функцию можно записать проще:
Это сложная логарифмическая функция. Применяя правило о том, что постоянный множитель можно выносить за знак производной, а затем формулу (2) при
получаем
Нет времени вникать в решение? Можно заказать работу!
Если функция дана в виде
,
то перед тем, как находить её производную, часто бывает выгодно прологарифмировать эту функцию.
Это прежде всего случаи, когда требуется найти производную произведения или частного функций, а также степенной функции, когда основание и степень — функции.
На основании свойств сложных функций доказано, что производная функции, вид которой приведён выше, может быть найдена по формуле
.
Пример 3. Найти производную функции
.
Решение. Логарифмируем обе части равенства и находим:
Решение. Окончательно находим производную данной функции:
Пример 4. Найти производную функции
.
Решение. Логарифмируем обе части равенства:
Дифференцируем:
Выражаем и находим производную данной функции:
Пример 5. Найти производную функции
Посмотреть правильное решение и ответ.
Пример 6. Найти производную функции
Посмотреть правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
- Применение производной к исследованию функций
- Экстремумы функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
Средство создания графиков логарифмических функций — MathCracker.
 com
comАлгебра Решатели
Инструкции: Этот конструктор графиков логарифмических функций позволяет построить график логарифмической функции или сравнить график двух логарифмических функций. Вам необходимо указать базу \(b\) каждой из функций \(f(x) = \log_b x\).
Базовая функция 1 (пример 10, 2, e и т. д.) =
Базовая функция 2 (пример 10, 2, e и т. д.) =
Оценочные баллы (необязательно.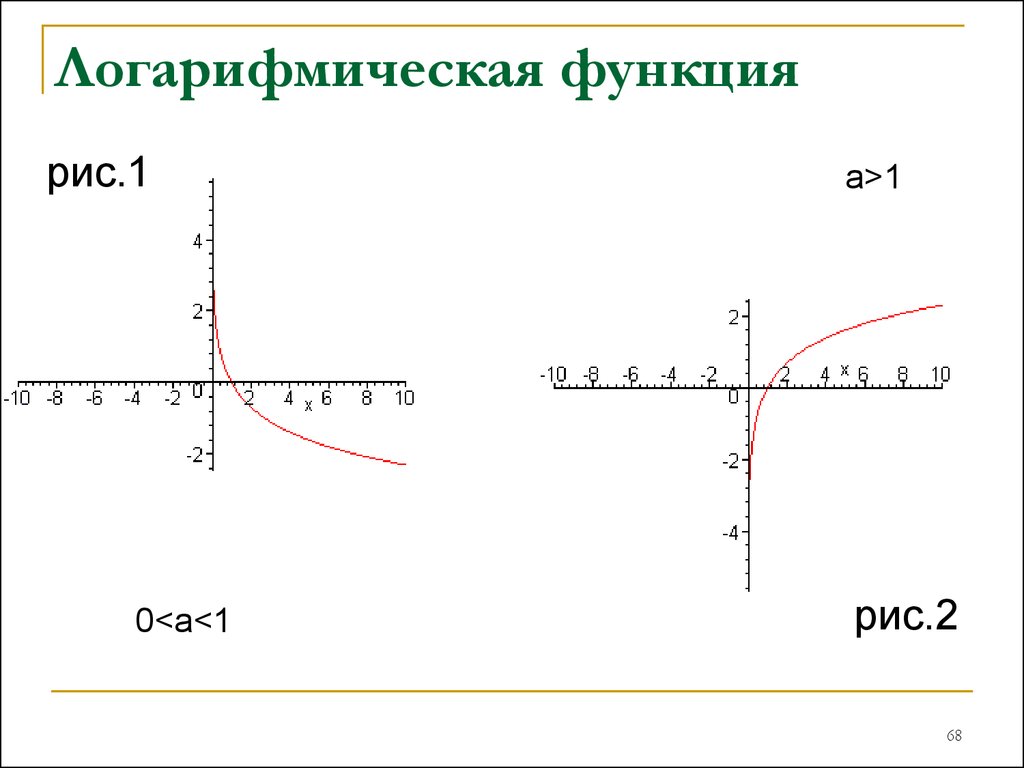 Разделены запятой или пробелом) =
Разделены запятой или пробелом) =
Этот построитель графиков позволяет отображать две логарифмические функции и, при необходимости, оценивать две функции по нескольким значениям.
Эти логарифмические функции, которые можно изобразить с помощью этого калькулятора, следующие:
\[f(x) = \log_bx\]
Итак, чтобы получить соответствующие графы, нужно просто указать основания.
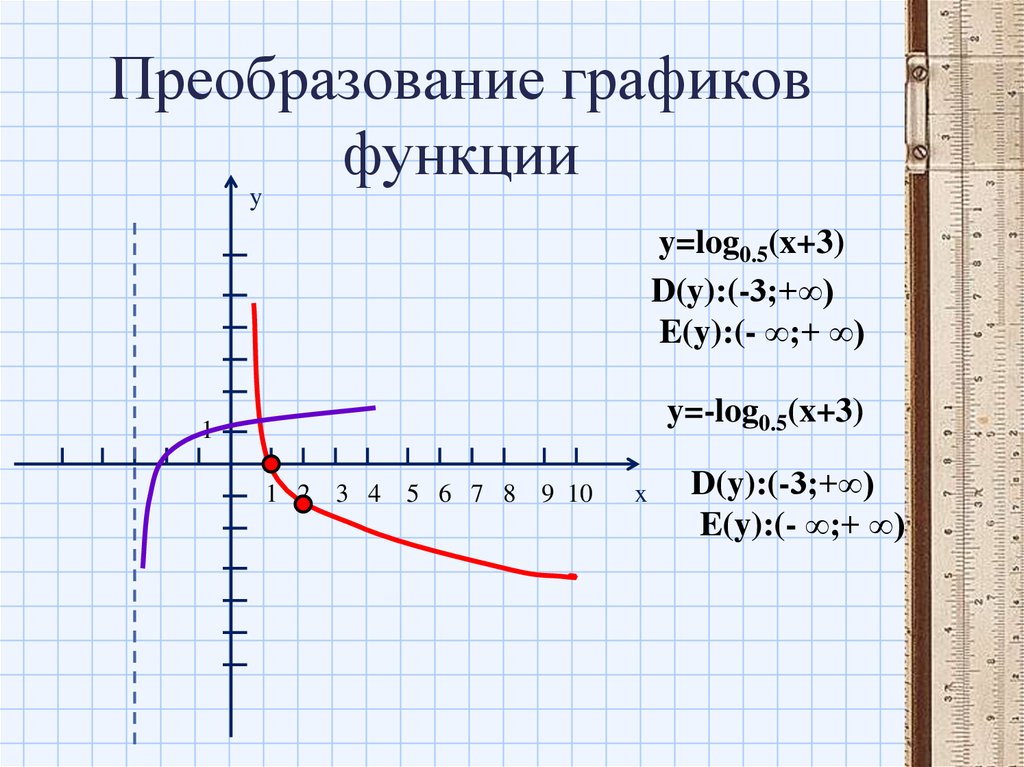
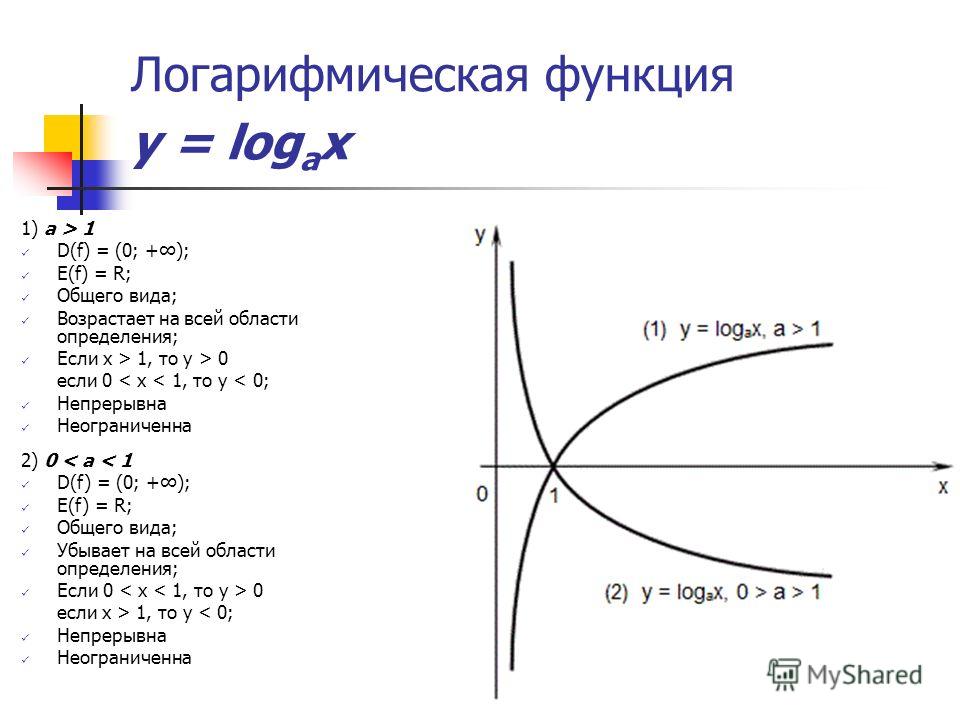
Что является обратной логарифмической функцией и как ее изобразить?
Обратные логарифмические функции
экспоненциальные функции
. x\).
x\).
С точки зрения их графиков график логарифмической функции и соответствующая экспоненциальная обратная функция симметричны относительно 45 о прямая линия.
Как построить график экспоненциальной функции
Экспоненциальная функция указанного выше вида будет иметь характерный экспоненциальный вид, и ее общий вид будет зависеть от того, положительна или отрицательна скорость \(r\).
Для положительной скорости \(r\) мы будем иметь
экспоненциальный рост
, а для отрицательной скорости \(r\) будем иметь
экспоненциальный спад
.
В чем польза логарифмической бумаги?
Логарифмическая бумага — это особый тип бумаги, в котором шкала изменена таким образом, что теперь логарифмические функции отображаются как линейные функции. У них было свое время, в настоящее время графические устройства (такие как это) легко доступны и делают логарифмическую бумагу довольно устаревшей.
Как оценить логарифмическую функцию?
Часто вам нужно будет оценить
логарифмическая функция для прохождения через две точки
, и для этой цели вам будут даны две точки, и вы будете решать систему для оценки необходимых параметров, чтобы логарифмическая функция проходила через эти точки.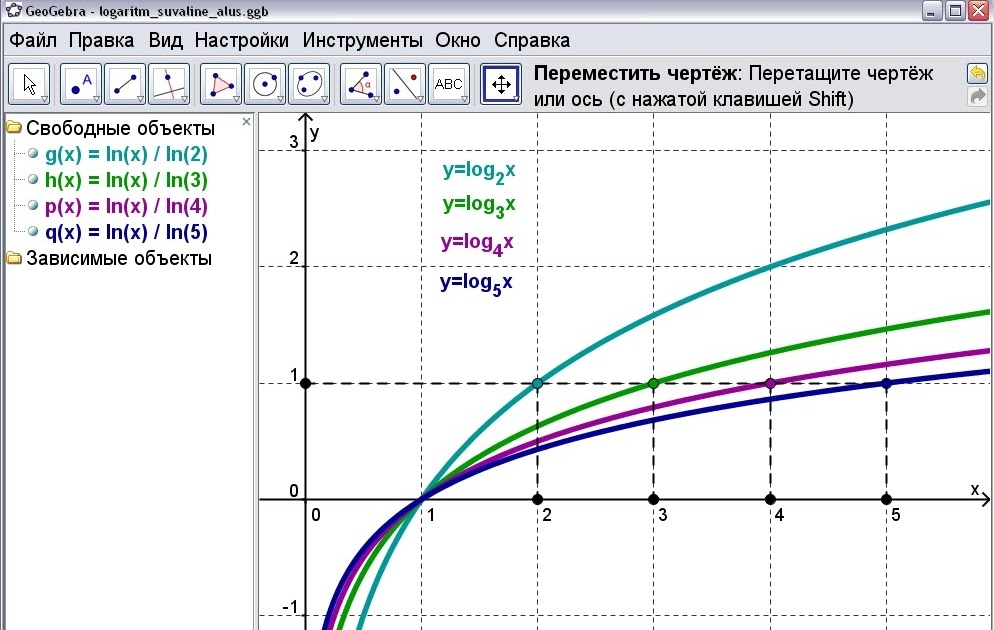
Алгебра Калькулятор Алгебра Решатель Базовый пакет алгебры Создатель графиков Логарифм Функция Графический редактор Создатель графика логарифмических функций
графическое представление функции log(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функциональное исследование ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функциональное исследование ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
Операторы для использования в 9Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие обычные математические функции :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- arctan (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус графика
- арксинус (арксинус), арксинус графика
- arctan (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- cosec (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.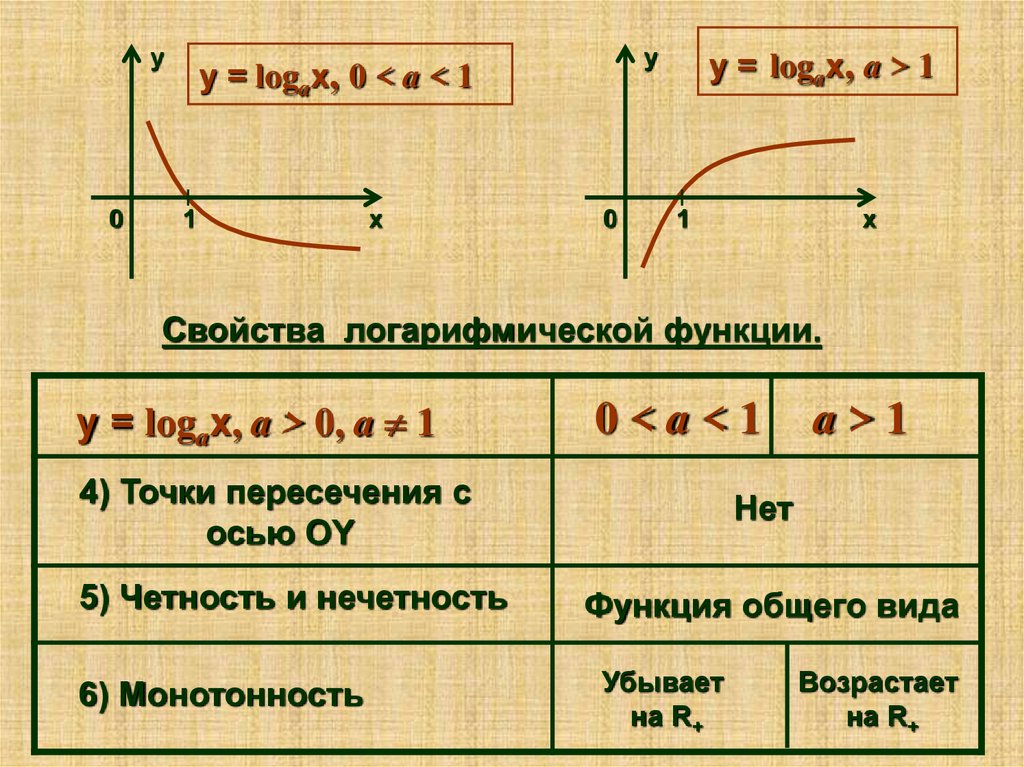
9Построитель кривых 0052 также можно использовать для вычисления производной функции и к участок он для этого, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.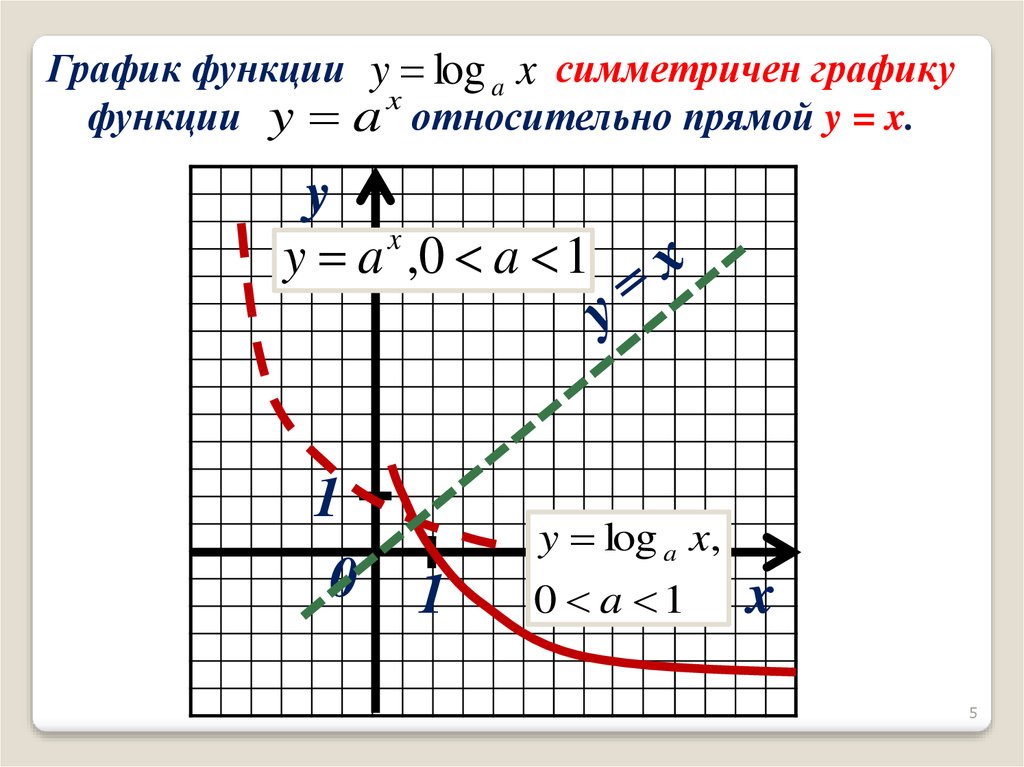
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика.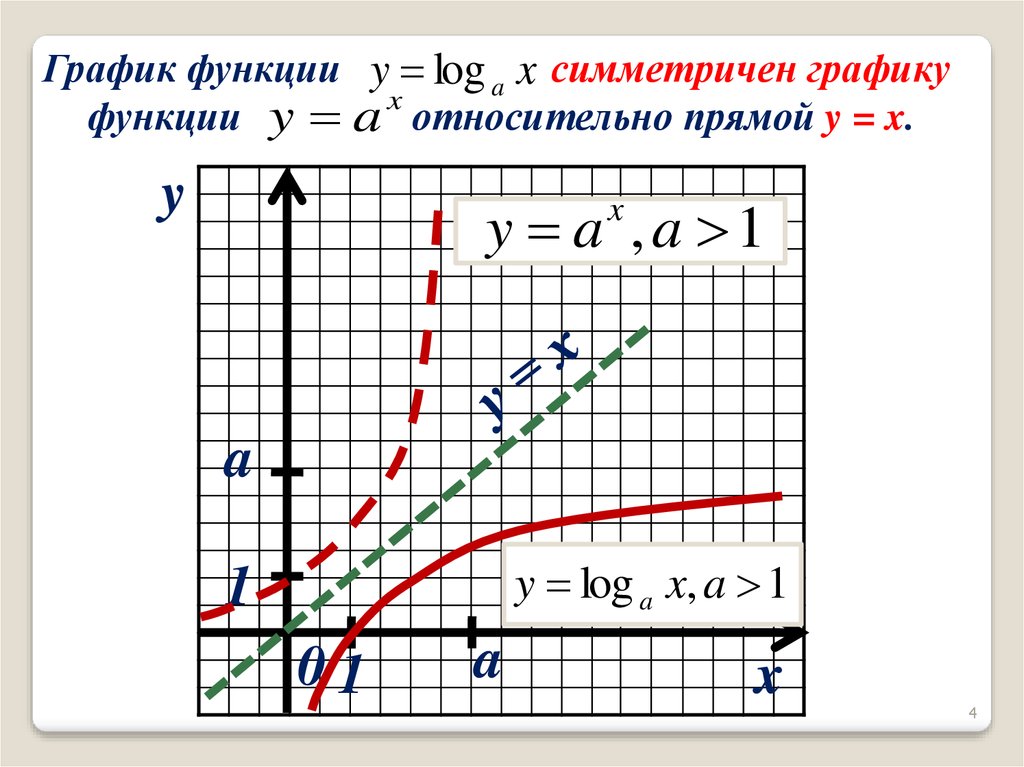 Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.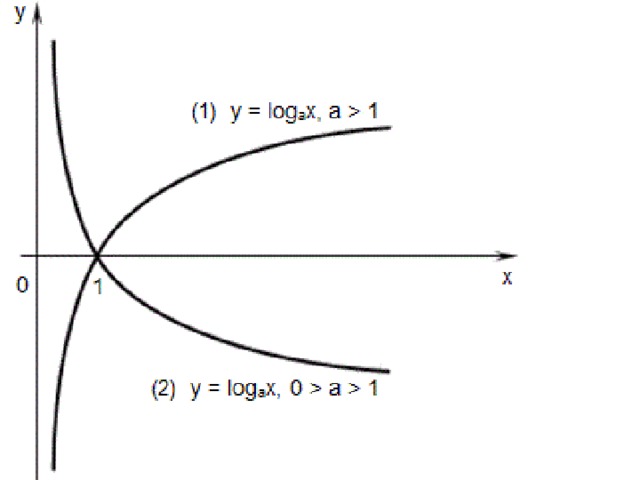

 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения