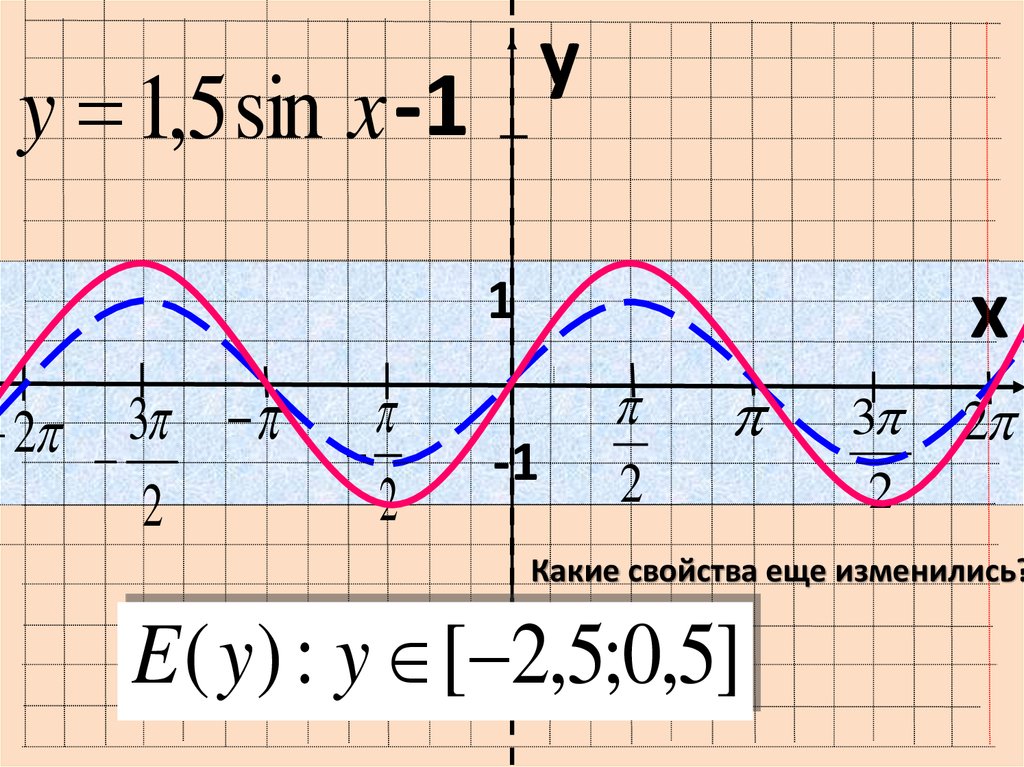
Урок «Периодичность функций y=sinx, y=cosx». Исследование функции на периодичность
>> Периодичность функций у = sin х, у = cos х
§ 11. Периодичность функций у = sin х, у = cos х
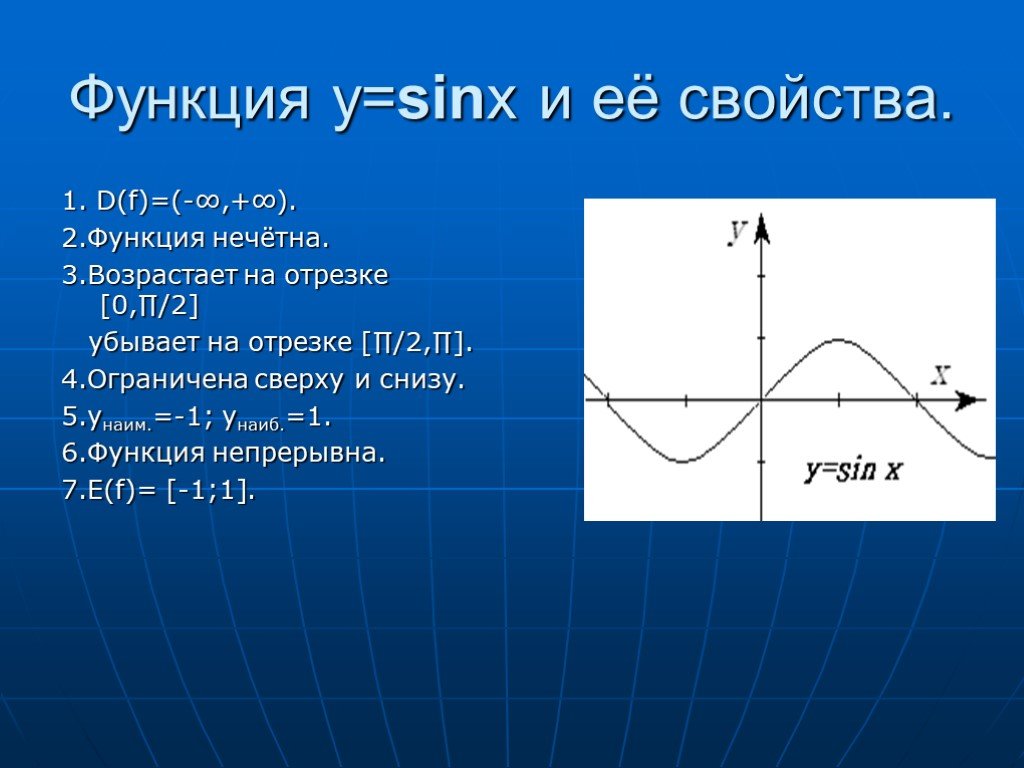
В предыдущих параграфах мы использовали семь свойств функций : область определения, четность или нечетность, монотонность, ограниченность, наибольшее и наименьшее значения, непрерывность, область значений функции. Использовали мы эти свойства либо для того, чтобы построить график функции (так было, например, в § 9), либо для того, чтобы прочитать построенный график (так было, например, в § 10). Теперь настал благоприятный момент для введения еще одного (восьмого) свойства функций, которое прекрасно просматривается на построенных выше графиках функций у = sin х(см. рис. 37), у=соs х(см. рис. 41).
Определение. Функцию называют периодической, если существует такое отличное от нуля число T, что для любого х из множествах выполняется двойное равенство :
Число Т, удовлетворяющее указанному условию, называют периодом функции у = f(х).
Отсюда следует, что, поскольку для любого х справедливы равенства:
то функции у = sin х, у=соs х являются периодическими и число 2п служит периодом и той, и другой функции.
Периодичность функции — это и есть обещанное восьмое свойство функций.
А теперь посмотрите на график функции у = sin х (рис. 37). Чтобы построить синусоиду, достаточно построить одну ее волну (на отрезке а затем сдвинуть эту волну по оси х на В итоге с помощью одной волны мы построим весь график.
Посмотрим с этой же точки зрения на график функции у =соs х (рис. 41). Видим, что и здесь для построения графика достаточно сначала построить одну волну (например, на отрезке
А затем сдвинуть ее по оси х на
Обобщая, делаем следующий вывoд.
Если функция у = f(х) имеет период Т, то для построения графика функции нужно сначала построить ветвь (волну, часть) графика на любом промежутке длины Т (чаще всего берут промежуток с концами в точках а затем сдвинуть эту ветвь по оси х вправо и влево на Т, 2Т, ЗТ и т.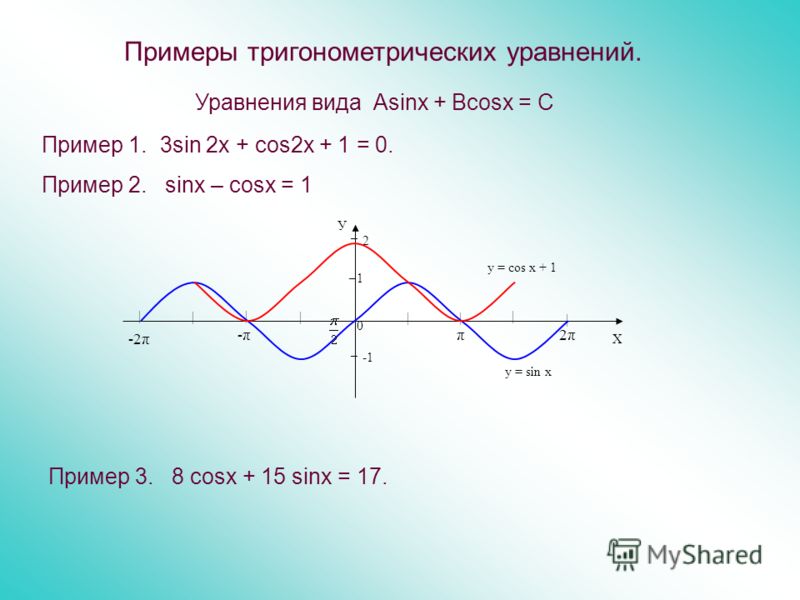
У периодической функции бесконечно много периодов: если Т — период, то и 2Т — период, и ЗТ — период, и -Т — период; вообще периодом является любое число вида KТ, где к = ±1, ±2, ± 3… Обычно стараются, если это возможно, выделить наименьший положительный период, его называют основным периодом.
Итак, любое число вида 2пк, где к = ±1, ± 2, ± 3,является периодом функций у = sinп х, у=соs х; 2п- основной период и той, и другой функции.
Пример. Найти основной период функции:
а) Пусть Т — основной период функции у = sin х. Положим
Чтобы число Т было периодом функции, должно выполняться тождество Но, поскольку речь идет об отыскании основного периода, получаем
б) Пусть Т — основной период функции у =соs 0,5х. Положим f(х)=соs 0,5х. Тогда f(х + Т)=соs 0,5(х + Т)=соs (0,5х + 0,5Т).
Чтобы число Т было периодом функции, должно выполняться тождество соs (0,5х + 0,5Т)=соs 0,5х.
Значит, 0,5т = 2пп. Но, поскольку речь идет об отыскании основного периода, получаем 0.
5Т = 2 л, Т =4л.
Обобщением результатов, полученных в примере, является следующее утверждение: основной период функции
А.Г. Мордкович Алгебра 10 класс
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x
(см.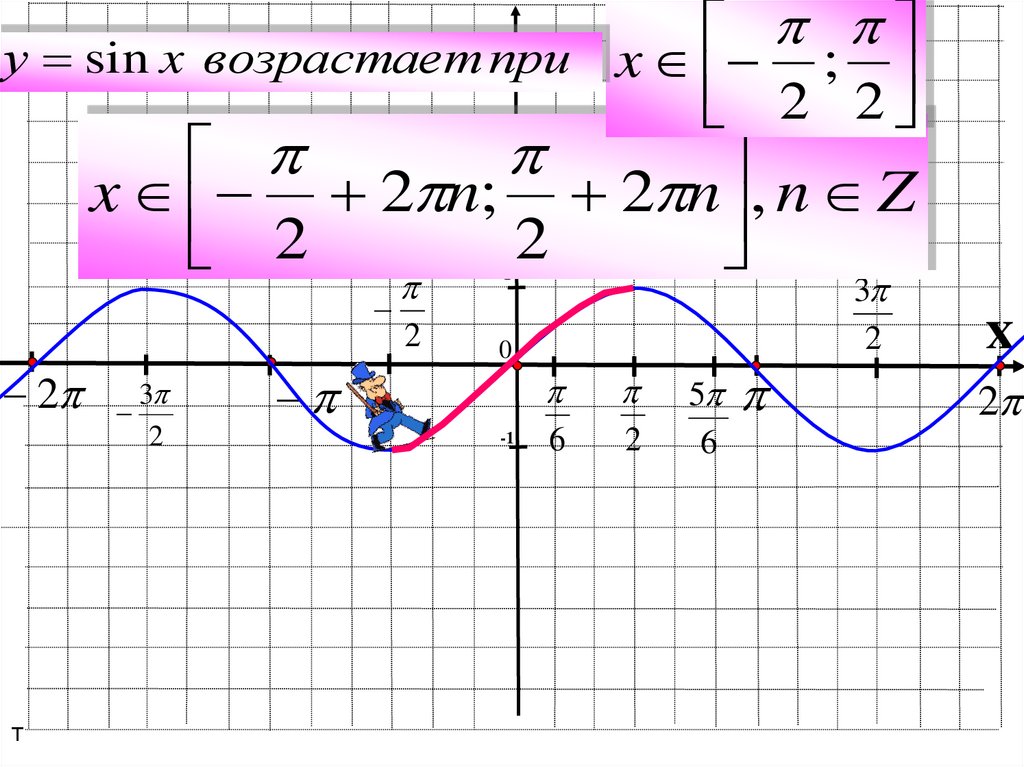
доказательство непрерывности). Их основные свойства представлены в таблице (n
— целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.
Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.
Если F(x) — с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку периодически повторяется, то должна повторяться .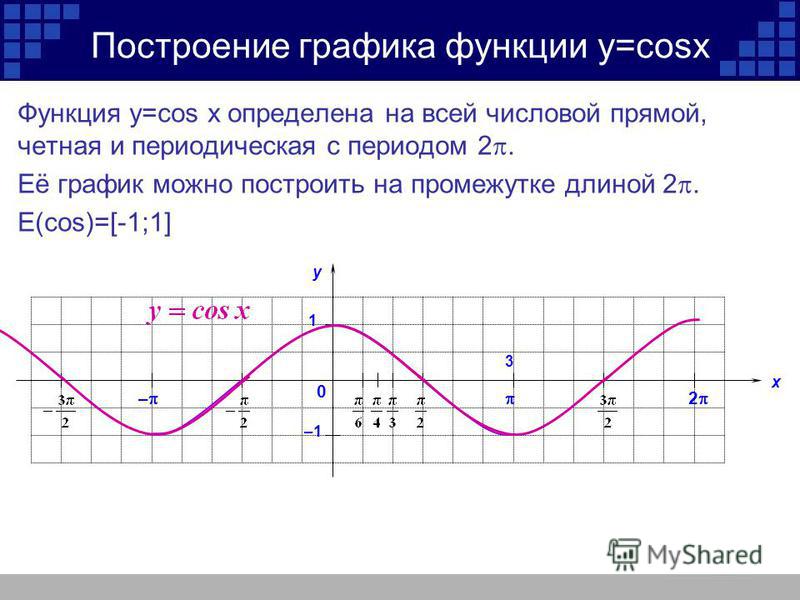
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете функции по горизонтали именно в столько раз
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Однако если соотношение периодов , то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.
Источники:
- Теоретические сведения о функциях
Многие математические функции имеют одну особенность, облегчающую их построение, — это периодичность , то есть повторяемость графика на координатной сетке через равные промежутки.
Инструкция
Самыми известными периодическими функциями математики синусоида и косинусоида.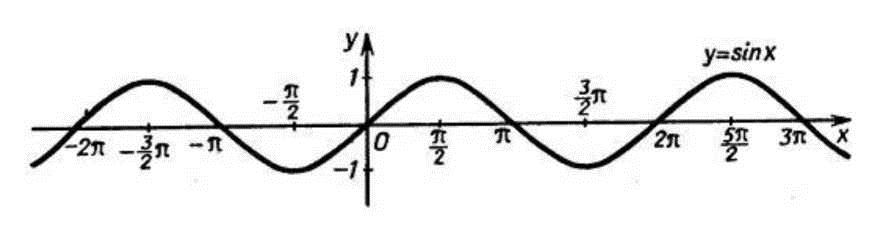
Эти функции имеют волнообразный и основной период, равный 2П. Также частным случаем периодической функции является f(x)=const. На позицию х подходит любое число, основного периода данная функция не имеет, так как представляет собой прямую.
Вообще функция является периодической, если существует целое число N, которое от нуля и удовлетворяет правилу f(x)=f(x+N), таким образом обеспечивая повторяемость. Период функции — это и есть наименьшее число N, но не ноль. То есть, например, функция sin x равна функции sin (x+2ПN), где N=±1, ±2 и т.д.
Иногда при функции может множитель (например sin 2x), который увеличит или сократит период функции. Для того чтобы найти период по
Самостоятельная работа 5 Функции y = sinx, y = cosx, их свойства и графики
Самостоятельная работа 5 Функции y = sinx, y = cosx, их свойства и графики
|
03.2013
Самостоятельная работа 1.  5Функции y = sinx, y = cosx, их свойства и графики Вариант 1 А1. Постройте график функции: . А2. Найдите наибольшее и наименьшее значение функции на отрезке . А3.Докажите, что функция является нечетной. _____________________________________________________ В1. Решите графически уравнение: . Задания А1-А3 соответствуют уровню обязательной подготовки. ____________________________________________________________________ Самостоятельная работа 1.5 Функции y = sinx, y = cosx, их свойства и графики Вариант 2 А1. Постройте график функции: . А2. Найдите наибольшее и наименьшее значение функции на отрезке . А3.Докажите, что функция является четной. _____________________________________________________ В1. Решите графически уравнение: . Задания А1-А3 соответствуют уровню обязательной подготовки. |
doc
| «Функции, их свойства и графики» По графику функции у=f(x), изображенному на рисунке 1, определите промежуток, на котором функции убывает | Свойства и графики тригонометрических функций Наибольшее и наименьшее значение функции. Нули функции. Промежутки знакопостоянства | ||
| Тема: «тригонометрические функции и их графики» цели урока: Обобщить материал по теме : «Тригонометрические функции и их графики» … | К самостоятельной работе №12 10 алгебра Понятие логарифма. Свойства логарифмов (п. 1 2) Постройте графики функций и перечислите их свойства: а; б. Запишите их свойства | ||
| Тест «Общие свойства функции» 1 На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками и знаками коэффициентов k и b? | Решение уравнений. Цель: разработать компьютерную модель нахождения корней уравнения x 3 sinx = 0 График и с заданной точностью с помощью метода Подбора параметра задать значения функции и найти значение аргумента функции, которое.  .. | ||
| Самостоятельная работа по теме: «Наибольшее, наименьшее значения функции». 1 вариант. 1 Найдите наименьшее значение функции | Самостоятельная работа №1 (6 ч.) Самостоятельная работа №1 (6 ч.) Слушателя: Баранецкой Олеси Михайловны, г. Долгопрудный, мбоу школа №3 | ||
| Функции и графики Математика – наука о математических моделях. Модели описываются в математике специфическим языком: термины, обозначения, символы,… | Контрольная работа №3. Вариант 1 Изобразите схематически график функции и перечислите ее свойства: а) б) Докажите, что функция f(x) = 4x tgx является нечётной |
Разместите кнопку на своём сайте:
Документы
База данных защищена авторским правом ©lib2.podelise.ru 2000-2013
При копировании материала обязательно указание активной ссылки открытой для индексации.
обратиться к администрации
| Документы |
На тех же осях начертите график y = sin x и y = cos x . Найдите все точки пересечения.
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«На тех же осях нарисуйте график y = sin x и y = cos x. Найдите все точки пересечения». eNotes Editorial , 12 марта 2011 г., https://www.enotes.com/homework-help/same-axes-sketch-graphs-y-sin-y-cosa-find-all-249211. По состоянию на 3 февраля 2023 г.
Я не могу набросать нужные вам здесь графики. Точки пересечения можно определить следующим образом.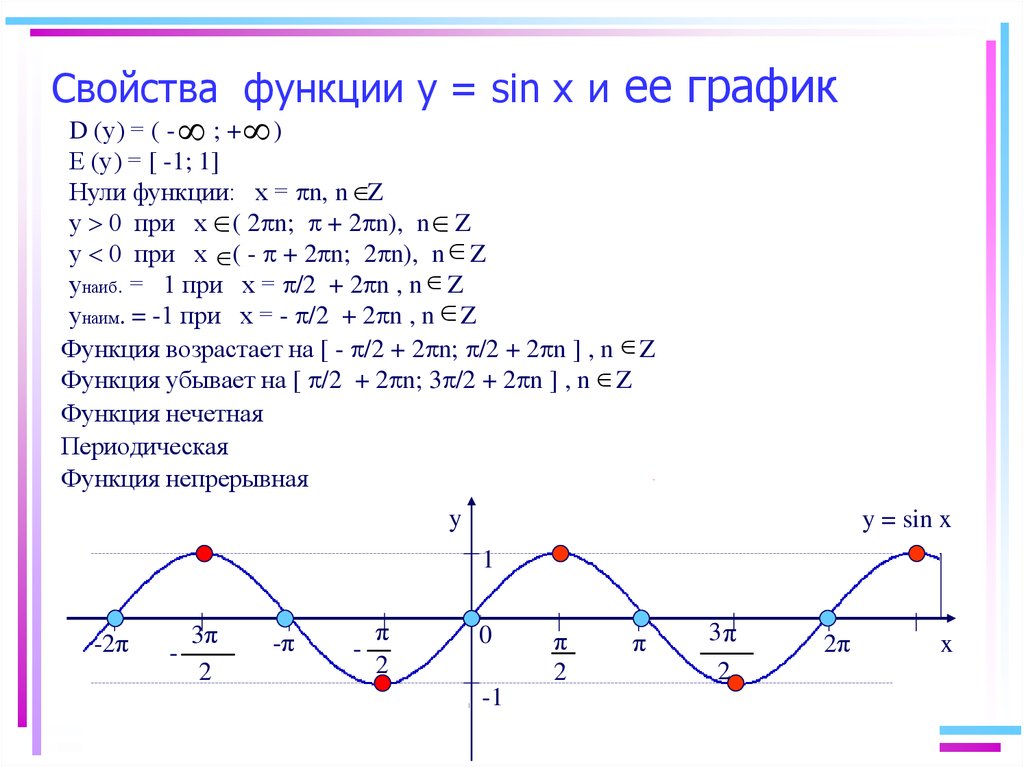
Чтобы найти точки пересечения оси x с y = sin x, приравняем y = sin x = 0. Получим x = arc sin 0 = 0 и pi. Так как функция синуса периодична. График пересекает ось x во всех точках, заданных (2*n*pi, 0) и (pi + 2*n*pi, 0)
Аналогично график y = cos x пересекает ось x в точках (pi/2 + 2*n*pi, 0) и (3*pi/2 + 2*n*pi , 0)
y = sin x пересекает ось y в точке (0, 0), а y = cos x пересекает ось y в точке (0, 1).
Два графика пересекаются в точке x, соответствующей sin x = cos x
=> tan x = 1
=> x = arc tan 1
=> x = pi/4
Точки пересечения два графика: (pi/4 + 2*n*pi, 1/sqrt 2) и (5pi/4 + 2*n*pi, -1/sqrt 2)
y = sin x пересекает ось x в точках (2*n*pi , 0) и (pi + 2*n*pi , 0). y = cos x пересекает ось x в точках (pi/2 + 2*n*pi, 0) и (3*pi/2 + 2*n*pi, 0).
y = sin x пересекает ось y в точке (0, 0) и y = cos x пересекает ось y в точке (0, 1).
Точками пересечения y = sin x и y = cos x являются (pi/4 + 2*n*pi, 1/sqrt 2) и (5pi/4 + 2*n*pi , -1/ кв 2)
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов воспитателя
математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответы воспитателя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ учителя
Математика
Последний ответ опубликован 15 мая 2012 г. в 7:13:43.
Как записать sin x через cos x?
1 Ответ учителя
Математика
Последний ответ опубликован 16 мая 2012 г.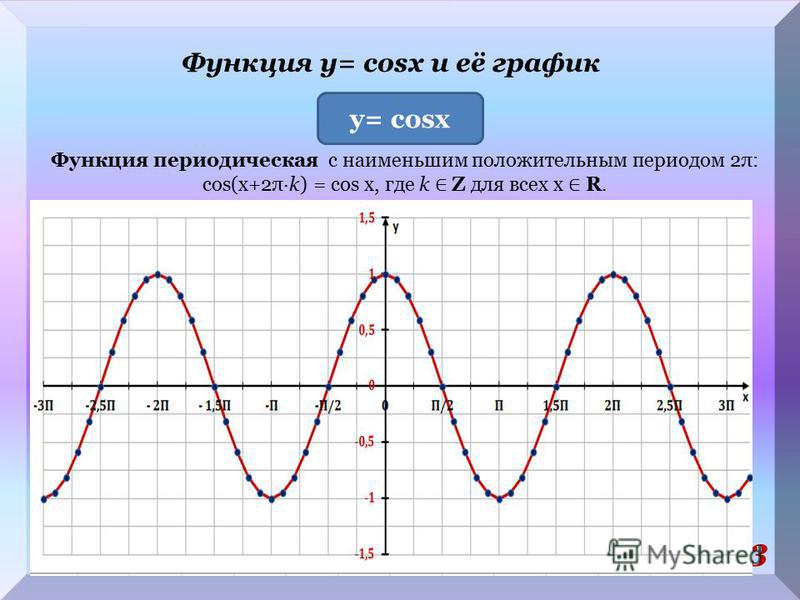
в 9:38:56.
Найдите значение log 20, не используя калькулятор
1 Ответ воспитателя
6.3 Изучение графиков первичного триггера
6.3 Изучение графиков основных тригонометрических функций
Полезные видеоролики
youtube.com/embed/6gL9SvbbnhM?wmode=transparent&autoplay=0&mute=0&theme=dark&controls=1&autohide=0&loop=0&showinfo=0&rel=0&enablejsapi=0″ frameborder=»0″ title=»External YouTube» aria-label=»External YouTube» data-testid=»youtube» allowfullscreen=»»> В качестве визуальной единицы измерения радиана выступает радиус. Однако это НЕ является адекватным представлением синусоидальных функций.
Вместо этого, когда мы рисуем точки, мы видим, что они повторяются. Это называется периодической функцией.
ПОПРОБУЙТЕ! Использование технологии построения графиков, например графического калькулятора, приведенного ниже, graph y=sinx, y=cosx и y=tanx.
Вы должны наблюдать следующие три графика:
Как видите, графики sinx и cosx имеют сходные черты, тогда как tanx — это совершенно другой график. Это связано с тем, что tanx по существу представляет собой sinx/cosx, и поэтому функция станет неопределенной, когда x будет равен нулям cosx (всякий раз, когда cosx = 0, знаменатель = 0, и функция становится неопределенной).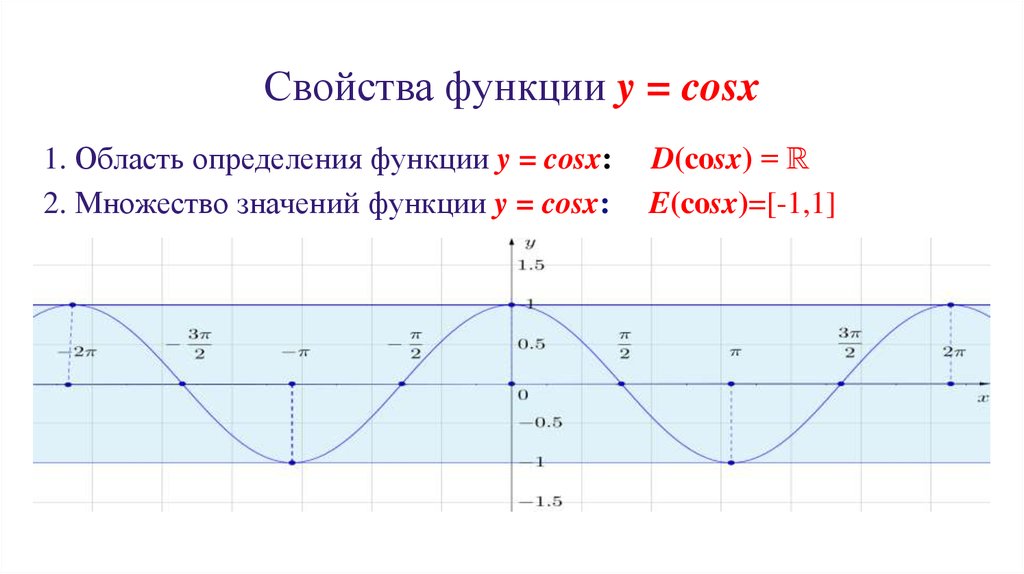
Вертикальные асимптоты предназначены для предотвращения этого и функции (точно так же, как в рациональных функциях!).
НАПОМИНАЕМ: Амплитуда тригонометрической функции — это расстояние до максимального и минимального значений. Его можно найти с помощью: макс. — мин ÷ 2.
Период тригонометрической функции — это время, за которое функция завершает полный цикл, прежде чем повторяется снова.
Уравнение оси симметрии — это уравнение горизонтальной линии, проходящей посередине между максимальным и минимальным значениями. Его можно найти с помощью: max + min ÷ 2,
Примеры вопросов
Уровень 1/2
Сравните графики y = sinx и y = cosx и включите описания следующих свойств: период, уравнение оси, амплитуда, макс. и минимальные значения, домен и диапазон.
Уровень 3
1) Почему для определения y = tan(x) требуются вертикальные асимптоты? Почему другие синусоидальные функции не требуют этих асимптот?
2) Напишите выражение, описывающее расположение точек пересечения x y = sin (x),
y = cos(x) и y = tan(x), где n — элемент I?.
Проверьте ответы
Верхнее
Другие полезные ссылки
Интерактивная математика
Клен мягкий
NRICH MATH
Ключевые концепции/Советы
График SIN (x) имеет период 2π, 2 -й. t≥уравнение оси равно 0 амплитуда равна 1 максимум = 1 минимум = -1 домен представлен как D= {θER} диапазон выражен как R= {yER// 1≥ y ≥ -1} Ключ точки находятся между 0 < θ < 2π или (0,0) (π/2,1) (π,0) (3π/2,-1) и (2π,0).
График cos(x) имеет одинаковые максимальные и минимальные значения, а также тот же домен и диапазон, хотя его ключевые точки находятся в диапазоне 0 < θ < 2π или (0,1) (π/2,0) (π,- 1) (3π/2,0) и (2π,1). То же EQN оси и амплитуды для родительской функции.
График tan(x) имеет период π, EQN оси равен 0, амплитуда не определена из-за его асимптот, нет максимальных или минимальных значений, его вертикальные асимптоты определены как θ= ±π/2,±3π/2 , ±5π/2…. Его диапазон определяется как R= {YER}, а его область значений определяется как {θER/0≠ ±π/2, ±3π/2, ±5π/2.