Высшая математика Т2
Высшая математика Т2
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.1. Предмет математики. Переменные и постоянные величины, множества § 1.2. Операции над множествами § 1.3. Символика математической логики § 1.4. Действительные числа § 1.5. Определение равенства и неравенства § 1.6. Определение арифметических действий 1.6.1. Общие соображения 1.6.2. Стабилизирующиеся последовательности 1.6.3. Определение арифметических действий § 1.7. Основные свойства действительных чисел § 1.8. Аксиоматический подход к понятию действительного числа § 1.9. Неравенства для абсолютных величин § 1.10. Отрезок, интервал, ограниченное множество § 1.11. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 2. Предел последовательности § 2.1. Понятие предела последовательности § 2.  2. Арифметические действия с переменными, имеющими предел§ 2.3. Бесконечно малая и бесконечно большая величины § 2.4. Неопределенные выражения § 2.5. Монотонные последовательности § 2.6. Число e § 2.7. Принцип вложенных отрезков § 2.8. Точные верхняя и нижняя грани множества § 2.9. Теорема Больцано-Вейерштрасса § 2.10. Верхний и нижний пределы § 2.11. Условие Коши сходимости последовательности § 2.12. Полнота и непрерывность множества действительных чисел Глава 3. Функция. Предел функции § 3.1. Функция 3.1.1. Функция от одной переменной. 3.1.2. Функции многих переменных. 3.1.3. Полярная система координат § 3.2. Предел функции § 3.3. Непрерывность функции § 3.4. Разрывы первого и второго рода § 3.5. Функции, непрерывные на отрезке § 3.7. Равномерная непрерывность функции § 3.8. Элементарные функции § 3.9. Замечательные пределы § 3.10. Порядок переменной. Эквивалентность Глава 4.  Дифференциальное исчисление функций одной переменной§ 4.1. Производная § 4.2. Геометрический смысл производной § 4.3. Производные элементарных функций § 4.4. Производная сложной функции § 4.5. Производная обратной функции § 4.6. Производные элементарных функций (продолжение) § 4.7. Дифференциал функции 4.7.1. Дифференцируемые функции 4.7.2. Дифференциал функции 4.7.3. Приближенное выражение приращения функции § 4.8. Другое определение касательной § 4.9. Производная высшего порядка § 4.10. Дифференциал высшего порядка. Инвариантное свойство дифференциала первого порядка § 4.11 Дифференцирование параметрически заданных функций § 4.12. Теоремы о среднем значении § 4.13. Раскрытие неопределенностей § 4.14. Формула Тейлора § 4.15. Ряд Тейлора § 4.16. Формулы и ряды Тейлора элементарных функций § 4.17. Локальный экстремум функции § 4.18. Экстремальные значения функции на отрезке § 4.19. Выпуклость кривой.  Точка перегиба§ 4.20. Асимптота графика функции § 4.21. Непрерывная и гладкая кривая § 4.22. Схема построения графика функции § 4.23. Вектор-функция. Векторы касательной и нормали Глава 5. неопределенные интегралы § 5.1. Неопределенный интеграл. Таблица интегралов § 5.2. Методы интегрирования § 5.3. Комплексные числа § 5.4. Теория многочлена n-й степени § 5.5. Действительный многочлен n-й степени § 5.7. Интегрирование иррациональных функций Глава 6. Определенный Интеграл § 6.1. Задачи, приводящие к понятию определенного интеграла, и его определение § 6.2. Свойства определенных интегралов § 6.3. Интеграл как функция верхнего предела § 6.4. Формула Ньютона – Лейбница § 6.5. Остаток формулы Тейлора в интегральной форме § 6.6. Суммы Дарбу. Условия существования интеграла § 6.7. Интегрируемость непрерывных и монотонных функций § 6.8. Несобственные интегралы § 6.  9. Несобственные интегралы от неотрицательных функций§ 6.10. Интегрирование по частям несобственных интегралов § 6.11. Несобственный интеграл с особенностями в нескольких точках Глава 7. Приложения интегралов. Приближенные методы § 7.1. Площадь в полярных координатах § 7.2. Объем тела вращения § 7.3. Гладкая кривая в пространстве. Длина дуги § 7.4. Кривизна и радиус кривизны кривой. Эволюта и эвольвента § 7.5. Площадь поверхности вращения § 7.6. Интерполяционная формула Лагранжа § 7.7. Квадратурные формулы прямоугольников и трапеций § 7.8. Формула Симпсона Глава 8. Дифференциальное исчисление функций многих переменных § 8.1. Предварительные сведения § 8.2. Предел функции § 8.3. Непрерывная функция § 8.4. Частные производные и производная по направлению § 8.5. Дифференцируемые функции § 8.6. Применение дифференциала в приближенных вычислениях § 8.7. Касательная плоскость. Геометрический смысл дифференциала § 8.  8. Производная сложной функции. Производная по направлению. Градиент8.8.1. Производная сложной функции 8.8.2. Производная по направлению 8.8.3. Градиент функции 8.8.4. Однородные функции § 8.9. Дифференциал функции. Дифференциал высшего порядка § 8.11. Замкнутое множество § 8.12. Непрерывная функция на замкнутом ограниченном множестве § 8.13. Экстремумы § 8.14. Нахождение наибольших и наименьших значений функции § 8.15. Теорема существования неявной функции § 8.16. Касательная плоскость и нормаль § 8.17. Системы функций, заданных неявно § 8.18. Отображения § 8.19. Условный (относительный) экстремум Глава 9. Ряды § 9.1. Понятие ряда § 9.2. Несобственный интеграл и ряд § 9.3. Действия с рядами § 9.4. Ряды с неотрицательными членами § 9.5. Ряд Лейбница § 9.6. Абсолютно сходящиеся ряды § 9.7. Условно сходящиеся ряды с действительными членами § 9.8. Последовательности и ряды функций. 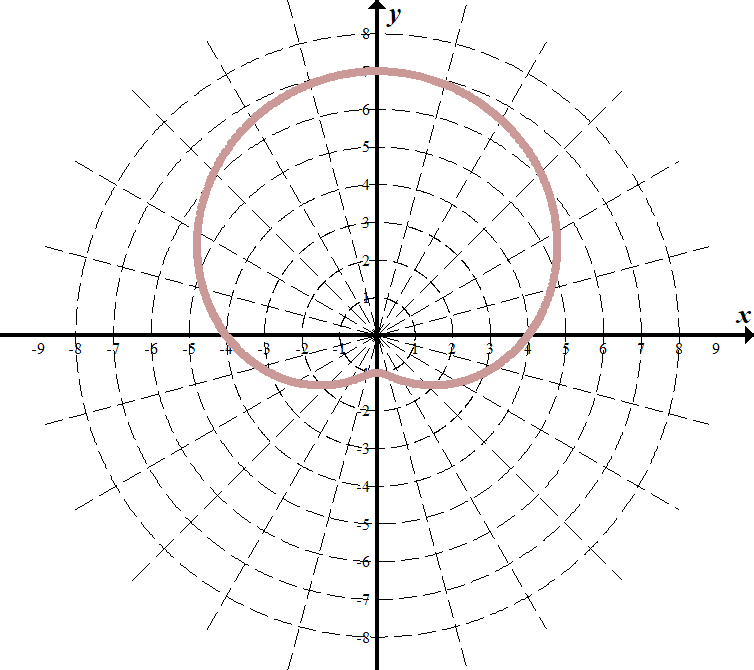 Равномерная сходимость§ 9.9. Интегрирование и дифференцирование равномерно сходящихся рядов § 9.10. Перемножение абсолютно сходящихся рядов § 9.11. Степенные ряды § 9.12. Дифференцирование и интегрирование степенных рядов § 9.13. Функции exp(z), sinz, cosz от комплексного переменного § 9.14. Ряды в приближенных вычислениях § 9.15. Понятие кратного ряда § 9.16. Суммирование рядов и последовательностей |
Polar Coordinates — полезнее, чем вы думали!
Наверняка вы хотя бы пару раз экспериментировали с фильтром полярных координат (Polar coordinates), но каждый раз получали совсем не то, что ожидали. Настало время с этим разобраться, и наконец-то сделать этот фильтр одним из полезнейших инструментов!
Фильтр полярных координат — гораздо более функциональный инструмент, чем многие думают. Теперь откиньтесь и расслабьтесь, а я расскажу вам о принципе работы фильтра полярных координат с математической точки зрения.
Учтите, что есть две опции в диалоговом окне фильтра — Rectangular to Polar и Polar to Rectangular. Обычно конвертация Rectangular to Polar значительно более полезна.
Rectangular и Polar — это два типа графиков. Картинки иллюстрируют два этих метода: первый график называется «прямоугольная система координат», она также известна как Декартовская. Прямоугольная система координат используется на низших уровнях алгебры. Центральная точка прямоугольной системы называется началом координат. Горизонтальная ось — ось x, а вертикальная — ось y. Координаты точки отображаются положением ее относительно оси x и y (расстоянием от начала координат по горизонтали и вертикали).
Полярная система координат сильно отличается от прямоугольной. Она используется в тригонометрии и других исчислениях. В полярной системе координат положение точки определяется как (R, Q), где R — полярный радиус или расстояние точки от начала координат, а Q — угол, образуемый полярным радиусом и полярной осью.
На рисунке ниже графики описывают один период синусоиды в прямоугольной и полярной системе координат. Сам график выделен голубым цветом. Графические изображения состоят из точек (пикселей). В режиме «Rectangular to polar» Photoshop конвертирует координаты каждой точки из прямоугольной системы в полярную. Следующая таблица показывает прямоугольные и полярные координаты для одних и тех же точек синусоиды.
| Rectangular Coordinates (x, y) | Polar Coordinates (r, q ) |
| (0, 0) | (0, 0) |
| (pi/4, sqrt(2)/2) | (sqrt(2)/2, pi/4) |
| (pi/2, 1) | (1, pi/2) |
| (3pi/4, sqrt(2)/2) | (sqrt(2)/2, 3pi/4) |
| (pi, 0) | (0, pi) |
| (5pi/4, -sqrt(2)/2) | (-sqrt(2)/2, 5pi/4) |
| (3pi/2, -1) | (-1, 3pi/2) |
| (7pi/4, -sqrt(2)/2) | (-sqrt(2)/2, 7pi/4) |
Примеры:
К этому моменту вы уже должны себе представлять принцип работы фильтра полярных координат.
Если вы все еще не понимаете, этот раздел поможет разобраться.
Это два наиболее простых примера — горизонтальные и вертикальные линии. Вы видите, что вертикальные линии после того, как к ним применен фильтр (конвертирующий координаты точек из прямоугольной системы в полярную), стали расходиться из центральной точки. На правой части картинки горизонтальные линии превратились в концентрически расходящиеся из центра круги. Согласитесь, просто?
С градиентами все сложнее, но ненамного! В сущности, принцип остается тем же. Горизонтальный линейный градиент сворачивается в круг, снизу наверх. Я добавил горизонтальные линии для наглядности. Этот круговой градиент создает приятный эффект, особенно, если вы сделаете копию левой половины изображения, перевернете ее по горизонтали и переместите на другую половину картинки.
Вертикальный линейный градиент, если его поляризировать, становится стандартным радиальным градиентом. Все еще ничего сложного, верно?
Ну а теперь попробуем еще немного усложнить.
Диагональный линейный градиент становится похож на спиральную заливку. Вы видите, в углах итогового изображения ошибки конвертации. Это происходит, потому что внешние грани касаются неопределенных бесконечностей при поляризации.
На втором примере, результат получился более приемлемым. Каждый сегмент выглядит так, как будто он был растянут по краю круга.
Ну вот, теперь вам должно быть совершенно ясно, как все происходит, когда вы применяете фильтр Полярных координат.
Применение:
Это фрагмент обоев для рабочего стола «Geotech» (Liquisoft™, Liquisoft.com).
Это мой любимый способ использования фильтра полярных координат. Чтобы достичь этого эффекта нарисуйте лини с разным наклоном и толщиной, каждую в новом слое. Примените фильтр «Rectangular to polar» на каждом слое и установите режим наложения слоев на «Color dodge». Установите непрозрачность каждого слоя на уровень примерно от 5 до 50%.
Затем примените эффект «Blur» (Размывание) на каждый слой. Эффект размывания может быть любым — Radial Blur, Gaussian Blur, Motion Blur или любой другой способ, который вам больше нравится — они все годятся!
Следующая иллюстрация содержит фрагмент других обоев от Liquisoft™ — «Corrosion«.
Белые «вихри» созданы как раз с использованием фильтра полярных координат. Этого эффекта можно достичь, нарисовав несколько параллельных линий под углом около 45 градусов и применив на них конвертацию «Rectangular to polar«. Теперь, как в прошлом примере, нужно уменьшить непрозрачность, применить размывание, а потом дублировать слои, пока не добьетесь нужного эффекта.
Может быть, фильтр «Polar Coordinates» и не столь полезен, как размывание по Гауссу, эффекты света и некоторые другие фильтры, но все равно это замечательный инструмент в вашем персональном наборе инструментов Photoshop. Экспериментируйте с ним, и я гарантирую, вы останетесь довольны результатами!
Источник: GurusNetwork
Как строить графики полярных уравнений
••• Comstock/Comstock/Getty Images
Обновлено 24 апреля 2017 г.
Коллектив редакции
Полярные уравнения представляют собой математические функции, представленные в виде R = f (θ). Чтобы выразить эти функции, вы используете полярную систему координат. График полярной функции R представляет собой кривую, состоящую из точек в виде (R, θ). Из-за кругового аспекта этой системы с помощью этого метода легче строить графики полярных уравнений.
Понимание полярных уравнений
Учтите, что в полярной системе координат точка обозначается как (R, θ), где R — полярное расстояние, а θ — полярный угол в градусах.
Используйте радианы или градусы для измерения θ. Чтобы преобразовать радианы в градусы, умножьте значение на 180/π. Например, π/2 X 180/π = 90 градусов.
Знайте, что существует много форм кривых, заданных полярными уравнениями. Некоторые из них представляют собой круги, лимаконы, кардиоиды и кривые в форме розы. Кривые Лимакона имеют вид R = A ± B sin (θ) и R = A ± B cos (θ), где A и B — константы.
Кардиоидные (сердцевидные) кривые являются особыми кривыми семейства лимаконов. Кривые в виде лепестков розы имеют полярные уравнения в форме R = A sin (nθ) или R = A cos (nθ). Когда n нечетное число, кривая имеет n лепестков, а когда n четное, кривая имеет 2n лепестков.
Упрощение построения полярных уравнений
При построении графиков этих функций обратите внимание на симметрию. В качестве примера используйте полярное уравнение R=4 sin(θ). Вам нужно только найти значения для θ между π (Pi), потому что после π значения повторяются, поскольку функция синуса симметрична.
Выберите значения θ, которые делают R максимальным, минимальным или нулевым в уравнении. В приведенном выше примере R = 4 sin (θ), когда θ равно 0, значение R равно 0. Таким образом, (R, θ) равно (0, 0). Это точка перехвата.
Аналогичным образом найдите другие точки пересечения.
График полярных уравнений
- Графический калькулятор
- Полярная диаграмма
Обратите внимание, что тема графического построения полярного уравнения обширна и существует много других форм кривых, кроме упомянутых здесь.
Пожалуйста, обратитесь к ресурсам для получения дополнительной информации о построении графиков. Более быстрый способ построения графиков полярных уравнений — использование ручного графического калькулятора или онлайн-калькулятора. При построении графиков полярных функций получаются сложные кривые, поэтому лучше всего отображать их, нанося точки.
Рассмотрим R= 4 sin(θ) в качестве примера, чтобы узнать, как построить график полярных координат.
Оцените уравнение для значений (θ) между интервалом от 0 до π. Пусть (θ) равно 0, π/6, π/4, π/3, π/2, 2π/3, 3π/4, 5π/6 и π. Рассчитайте значения для R, подставив эти значения в уравнение.
С помощью графического калькулятора определите значения R. Например, пусть (θ) = π/6. Введите в калькулятор 4 sin(π/6). Значение R равно 2, а точка (R, θ) равна (2, π/6). Найдите R для всех значений (θ) на шаге 2.
Нанесите на график результирующие (R, θ ) точки из шага 3, а именно (0,0), (2, π/6), (2.8, π/4), (3.46,π/3), (4,π /2), (3.46, 2π/3), (2.8, 3π/4), (2, 5π/6), (0, π) на миллиметровой бумаге и соедините эти точки. График представляет собой окружность с радиусом 2 и центром в точке (0, 2). Для большей точности построения графиков используйте полярную миллиметровую бумагу.
Нарисуйте уравнения для лимаконов, кардиоид или любой другой кривой, заданной полярным уравнением, следуя описанной выше процедуре.
Вещи, которые вам понадобятся
Пожалуйста, обратитесь к ресурсам для получения дополнительной информации о построении графиков. Более быстрый способ построения графиков полярных уравнений — использование ручного графического калькулятора или онлайн-калькулятора. При построении графиков полярных функций получаются сложные кривые, поэтому лучше всего отображать их, нанося точки.Статьи по теме
Советы
- Обратите внимание, что тема построения графика полярного уравнения обширна и существует множество других форм кривых, кроме упомянутых здесь. Пожалуйста, обратитесь к ресурсам для получения дополнительной информации о построении графиков.
- Более быстрый способ построения графиков полярных уравнений — использование ручного графического калькулятора или графического онлайн-калькулятора.
- При построении графиков полярных функций получаются сложные кривые, поэтому лучше всего отображать их в виде точек.
Об авторе
Эта статья была написана командой CareerTrend, отредактирована и проверена с помощью многоточечной системы аудита, чтобы наши читатели получали только самую лучшую информацию.
Чтобы задать свои вопросы или идеи или просто узнать больше о CareerTrend, свяжитесь с нами [здесь](http://careertrend.com/about-us).
Photo Credits
Comstock/Comstock/Getty Images
Полярные координаты — Math Insight
Полярные координаты — Math InsightПолярные координаты
В двух измерениях декартовы координаты $(x,y)$ задают положение точки $P$ на плоскости. Другой двумерной системой координат являются полярные координаты. Вместо расстояний со знаком вдоль двух осей координат полярные координаты определяют положение точки $P$ на плоскости через ее расстояние $r$ от начала координат и угол $\theta$ между отрезком прямой от начала координат. к $P$ и положительной оси $x$. Полярные координаты $(r,\theta)$ точки $P$ показаны на рисунке ниже.
Поскольку $r$ изменяется от 0 до бесконечности, а $\theta$ изменяется от 0 до $2\pi$, точка $P$, заданная полярными координатами $(r,\theta)$, покрывает каждую точку в самолет. Добавление $2\pi$ к $\theta$ возвращает нас к той же точке, поэтому, если бы мы позволили $\theta$ варьироваться в интервале, большем, чем $2\pi$, каждая точка имела бы несколько полярных координат.
Следовательно, мы обычно ограничиваем $\theta$ внутренним $0 \le \theta
Следующий апплет позволяет исследовать, как изменение полярных координат $r$ и $\theta$ перемещает точку $P$ по плоскости. Вы меняете полярные координаты с помощью ползунков и наблюдаете, как точка перемещается в декартовой плоскости. Вы также можете перемещать точку в декартовой плоскости и наблюдать, как меняются полярные координаты. Обратите внимание на неоднозначность полярных координат при $r=0$.
Полярные координаты. При изменении значений полярных координат $r$ и $\theta$ путем перетаскивания красных точек на ползунках синяя точка перемещается в соответствующую позицию $(x,y)$ в декартовых координатах. В качестве альтернативы, вы можете перемещать синюю точку в декартовой плоскости прямо с помощью мыши и наблюдать, как меняются полярные координаты на ползунках. Координата $r$ — это длина отрезка от точки $(x,y)$ до начала координат, а координата $\theta$ — это угол между отрезком и положительной осью $x$.
Дополнительная информация об апплете.
Формулы преобразования
Мы можем вычислить декартовы координаты точки с полярными координатами $(r,\theta)$, составив прямоугольный треугольник, показанный на рисунке ниже. Гипотенуза — это отрезок прямой от начала координат до точки, а его длина равна $r$. Проекция этого отрезка на ось $x$ является катетом треугольника, примыкающим к углу $\theta$, поэтому $x=r\cos\theta$. $y$-компонента определяется другой ветвью, поэтому $y=r\sin\theta$. Наша формула преобразования \начать{выравнивать} x &= r\cos\theta\notag\\ y &= r\sin\theta. \label{полярный_to_cartesian}\тег{1} \end{выравнивание} 92. \конец{выравнивание*}
Взяв соотношение $y$ и $x$ из уравнения \eqref{polar_to_cartesian}, можно получить формулу для $\theta$,
\начать{выравнивать*}
\frac{y}{x} &= \frac{r\sin\theta}{r \cos\theta} = \tan\theta.
\конец{выравнивание*}
Эту зависимость можно также увидеть из приведенного выше прямоугольного треугольника.
2}\notag\\
\theta &= \arctan \frac{y}{x}.
\label{cartesian_to_polar}\tag{2} \end{выравнивание}
Как насчет точки, где $(x,y)=(0,0)$? В этом случае угол $\theta$ определен неправильно. Вы могли бы просто принять это как $\theta=0$, чтобы быть конкретным.
Другой взгляд на полярные координаты
В приведенном выше апплете мы представили полярные координаты двумя отдельными точками на оси $r$ и оси $\theta$ (два ползунка). Мы также могли бы объединить эти две оси в одну плоскость $(r,\theta)$ (точно так же, как плоскость $(x,y)$ декартовых координат). Это простое изменение представления полярных координат в виде одной точки на полярной плоскости $(r,\theta)$ отражено в следующем апплете. Такой небольшой сдвиг в перспективе имеет больше последствий, чем вы можете себе представить, о чем вы можете прочитать на странице о полярных координатах как отображении из плоскости $(r,\theta)$ в плоскость $(x,y)$.
Полярные координаты с полярными осями. Красная точка на вставке полярных осей $(r,\theta)$ представляет собой полярные координаты синей точки на главных декартовых осях $(x,y)$.