Решение квадратных уравнений — презентация онлайн
Похожие презентации:
Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. Урок обобщения и систематизации знаний
Решение квадратных уравнений
Решение квадратных уравнений
Квадратные уравнения. Дорогу осилит идущий, а математику мыслящий
Неполные квадратные уравнения
Решение квадратных уравнений с помощью формул
Решение квадратных уравнений
Квадратное уравнение
Решение квадратных уравнений по формуле
1. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙОвчарова Л. В.
учитель математики
2. Задачи для учащихся
1. Различать типы квадратных уравнений изнать способы их решения.
2. Знать формулы для решения квадратных
уравнений.
3. Уметь решать квадратные уравнения.
3. Устная работа.
1. Проклассифицируйте уравнения по какому-топризнаку и выделите лишнее уравнение
а) 5х – х2 = 0
а) х2 – 9х +20 = 0
б) 4х2 – 25 = 0
б) 9х2 – 3х + 10 =0
в) 3х2 – х – 5 = 0
в) х2 + 5х – 1 = 0
г) 3х2 + 6 = 0
г) х2 + 4х – 2 = 0
4.
Проклассифицируйте уравнения по какому-то признаку и выделите лишнее уравнениеа) х2 – 4х + 7 = 0б) 2х2 – 3х + 19 = 0
в) 3х2 + 32х + 60 = 0
г) х2 + 12х + 32 = 0.
5. 2. Решите уравнения:
а) х2 – 4х + 3 = 0б)х2 + 3х – 4 = 0
в) 7х2 – 9х + 2 = 0
г) 5х2 – 8х + 3 = 0
(1 и 3)
(1 и -4)
(1 и 2/7 )
(1 и 3/5).
6. Задание. Каждое уравнение на экране впишите в таблицу, соответствующее указанному признаку и решите его в своих тетрадях.
1) х2 + 36 = 02) 5х2 – 6х – 8 = 0
3) 2х2 = 0
4) 5х2 – 8х + 3 = 0
5) (х – 2) (х + 3) = 0
6) х2 – 4х + 4 = 0
7) х2 – 6х + 8 = 0
8) 5х2 + 4х = 0
9) 2х2 + 3х + 1 = 0
10) 2х2 – 5х + 2 = 0
11) 7х2 – 3 = 0
7. Заполните таблицу
№Дополнительное
условие
Уравнение
Заполните
таблицу
1.
в=с=0
2.
с =0
ах2 + вх = 0
х1 = 0, х2 = — в/а
3.
в=0
ах2 + с = 0
4.
а 0
ах2 + вх + с = 0
5.
в – четное число
(в = 2k)
ах2 + 2kx + c = 0
а) х1,2 = ± √с/а
где – с/а 0.
б) если – с/а 0, то
решений нет
x1= (-b-√D)/2a
x2 = (-b+√D)/2a
где D = в2 – 4ас
х1 =(-k-√D1 )/a
6.
Теорема Виета
x2 + px + q = 0
7.
а) а + в + с = 0
б) а – в + с = 0
Выделение
двучлена
8.
9.
ах2 = 0
Корни
х1 = 0
х1 =(-k-√D1 )/a
ах2 + вх + с = 0
ах2 + вх = с = 0
квадрата ах2 + вх = с = 0
(х +b/2a )2 = D/4а2
Разложение на множители ах2 + вх = с = 0
а(х – х1)(х – х2) = 0
D1 = k2 – ac, где
k = b/2
x1 + x2 = — p
x1 x2 = q
х1 = 1, х2 = c/a
х1 = — 1, х2 =- c/a
x1= (-b-√D)/2a
x2 = (-b+√D)/2a
где D = в2 – 4ас
х1, х2
Пример
№
Уравнение
Корни
1.
Дополнительное
условие
в=с=0
ах2 = 0
х1 = 0
2.
с =0
ах2 + вх = 0
х1 = 0, х2 =
3.
в=0
ах2 + с = 0
4.
а 0
ах2 + вх + с = 0
а) х1,2 = ± ,
где — 0.
б) если — 0, то
решений нет
x1,2 = , где D = в2 – 4ас
7х2 – 3 = 0
х1,2 =
х2 + 36 = 0
решений нет
2х2 – 5х +2=0
D=9
x1=0,5; x2=2
5.
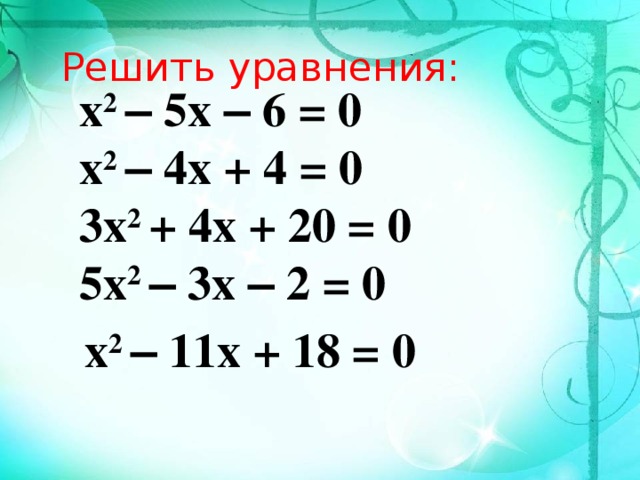
в – четное число
(в = 2k)
ах2 + 2kx + c = 0
х1,2 = ,
D1 = k2 – ac, где
k=
5×2-6x-8=0 k = -3
D1=9+40=49
x1=-0,8; x2= 2
6.
Теорема Виета
x2 + px + q = 0
x1 + x2 = — p
x1 x2 = q
x2 – 6x +8=0
x1= 4; x2 = 2
7.
а) а + в + с = 0
б) а – в + с = 0
ах2 + вх + с = 0
ах2 + вх = с = 0
х1 = 1, х2 =
х1 = — 1, х2 =-
5×2 -8x + 3=0
х1 =1; х2 =
2х2 +3х + 1=0
х1=-1; х2= —
8.
Выделение
квадрата двучлена
ах2 + вх = с = 0
(х + )2 =
x1,2 = , где D = в2 – 4ас
9.
Разложение
множители
х2 -4х + 4=0
(х – 2)2 = 0
х1 = 2
(х–2)(х+ 3)=0
х1=2; х2= -3
на ах2 + вх = с = 0
а(х – х1)(х – х2) = 0
х1, х2
—
Пример
2х2 = 0; х1 =0
5х2 + 4х = 0
х1=0; х2=-0,8
9. 2. Задание. Найдите ошибку в решении и подчеркните ее
1) 2х2 – 5х – 3 = 0D = 25 -4 2 3 = 1
х1 = = 1
х2 = = = 1,5
Ответ: 1 и 1,5
3) 5х + х2 – 6 = 0
D = 1 — 4 5 (-6) = 121
х1 = 3; х2 = — 8
Ответ: 3 и – 8.
2) х2 + 5х – 6 = 0
D = 25 -4 1 (-6) = 49
х1 = = 6
х2 = = -1
Ответ: 6 и – 1.
Психологическая разгрузка.
Сядьте спокойно,
закройте глаза,
положите руки на колени,
представьте, что вы едите на машине.
Вы приехали на озеро.
Ветерок.
Солнце.
Цветы.
Видите ромашку.
Нарисуйте кончиком носа в воздухе контуры ромашки.
Вдыхаем запахи, делаем вдох – выдох (три раза).
Глаза открыли.
Делаем вдох – выдох (два раза).
Дышите ритмично.
11. 3.Самостоятельная работа.
12. Задание на дом.
«Провести исследование и установить связь междукоэффициентами квадратного уравнения и его корнями
у следующих уравнений:
1) 6х2 – 13х + 6 = 0,
2) 5х2 — 26х + 5 = 0,
3) 2х2 + 5х + 2 = 0,
4) 4х2 + 17х + 4 = 0,
5) 3х2 – 10х + 3 = 0
13. Итог урока.
13 352
7
Итог урока.
English Русский Правила
результаты последних тиражей, таблица выпавших чисел
- Лотерейный супермаркет Столото /
- Сайт лотереи «Спортлото «4 из 20» /
- Архив тиражей
- Билеты
- Архив тиражей
- Проверка билетов
- Правила
- О лотерее
Поиск по дате или тиражу
Выделить номера в таблице комбинаций:
Дата
Тираж
Выпавшие числа
Cуперприз, ₽
05.
10.2022 13:00
5250
07 04 01 16 06 11 05 12
⚲
567 875 423
05.10.2022 10:00
5249
10 05 19 14 19 18 10 03
⚲
566 931 110
04.10.2022 22:00
5248
15 12 03 17 11 16 06 19
⚲
565 686 303
04.10.2022 16:00
5247
08 12 13 10 20 03 11 07
⚲
564 969 404
04.10.2022 13:00
5246
06 04 07 05 11 18 17 06
⚲
564 254 279
04.10.2022 10:00
5245
10 05 11 09 14 04 19 03
⚲
563 291 273
03.
10.2022 22:00
5244
15 12 08 10 14 06 18 13
⚲
562 011 643
03.10.2022 16:00
5243
13 11 03 10 07 15 18 20
⚲
561 240 383
03.10.2022 13:00
5242
17 14 19 15
⚲
560 546 689
03.10.2022 10:00
5241
04 07 01 15 18 17 12 04
⚲
559 582 106,50
02.10.2022 22:00
5240
13 17 12 06 18 04 17 12
⚲
558 323 031,50
02.10.2022 16:00
5239
15 14 10 17 14 06 17 05
⚲
557 500 314,50
02.
10.2022 13:00
5238
16 20 03 13 10 18 19 14
⚲
556 603 570
02.10.2022 10:00
5237
13 02 20 12 02 03 20 10
⚲
555 608 694,50
01.10.2022 22:00
5236
17 11 15 03 02 13 04 14
⚲
554 320 060,50
01.10.2022 16:00
5235
09 01 15 06 06 03 12 04
⚲
553 493 062
01.10.2022 13:00
5234
01 14 16 07 10 13 14 07
⚲
552 654 348
01.10.2022 10:00
5233
06 12 09 13 05 01 16 18
⚲
551 494 933
30.
5232
09 02 16 12 19 16 11 05
⚲
550 071 438,50
30.09.2022 16:00
5231
09 03 02 12 06 01 13 14
⚲
549 190 056,50
30.09.2022 13:00
5230
01 09 15 05 11 12 15 04
⚲
548 338 211
30.09.2022 10:00
5229
04 14 15 16 16 13 07 03
⚲
547 077 738
29.09.2022 22:00
5228
15 09 01 20 03 14 04 02
⚲
545 851 569
29.09.2022 16:00
5227
17 04 08 06 05 03 06 13
⚲
545 088 763
29.
09.2022 13:00
5226
12 01 08 03 10 18 04 01
⚲
544 318 884,50
29.09.2022 10:00
5225
08 10 15 11 10 15 11 08
⚲
543 561 765,50
28.09.2022 22:00
5224
14 04 10 19 03 13 01 10
⚲
542 314 443,50
28.09.2022 16:00
5223
18 05 10
⚲
541 528 633
28.09.2022 13:00
5222
01 07 13 14 14 20 06 11
⚲
540 811 552,50
28.09.2022 10:00
5221
13 14 01 07 11 16 08 17
⚲
539 839 135
27.
09.2022 22:00
5220
05 12 18 07 02 11 01 15
⚲
538 607 691
27.09.2022 16:00
5219
19 07 20 16 12 13 09 04
⚲
537 904 819
27.09.2022 13:00
5218
07 01 18 08 18 12 09 08
⚲
537 175 465,50
27.09.2022 10:00
5217
01 03 20 02 01 13 19 20
⚲
536 139 587,50
26.09.2022 22:00
5216
03 15 10 12 06 15 07 16
⚲
534 936 010,50
26.09.2022 16:00
5215
18 01 06 09 04 20 02 13
⚲
534 231 604
26.
09.2022 13:00
5214
02 01 05 11 04 09 03 10
⚲
533 535 791,50
26.09.2022 10:00
5213
13 15 02 11 15 19 02 01
⚲
532 632 489
25.09.2022 22:00
5212
20 17 13 05 19 11 14 06
⚲
531 438 298,50
25.09.2022 16:00
5211
04 17 02 01 02 06 17 10
⚲
530 671 617
25.09.2022 13:00
5210
10 18 17 20 04 15 09 19
⚲
529 903 086,50
25.09.2022 10:00
5209
12 03 05 11 04 03 19 14
⚲
528 972 681
24.
09.2022 22:00
5208
08 14 19 17 09 07 02 19
⚲
527 770 737
24.09.2022 16:00
5207
05 06 18 19 19 14 13 05
⚲
526 983 468,50
24.09.2022 13:00
5206
12 06 18 10 06 07 20 05
⚲
526 115 557,50
24.09.2022 10:00
5205
14 19 18 01 01 13 02 06
⚲
524 937 754
23.09.2022 22:00
5204
17 03 13 20
⚲
523 812 214
23.09.2022 16:00
5203
05 16 04 03 07 15 06 12
⚲
522 976 914
23.
09.2022 13:00
5202
02 06 18 14 01 09 12 16
⚲
522 150 935,50
23.09.2022 10:00
5201
11 20 05 01 08 12 17 20
⚲
521 041 466,50
Показать ещё
3-8Cremincios Sobre equação do 1º Grau com uma incógnita
Uma equação do 1º Grau com uma incógnita é aquela Que Pode Ser Escrita na forma Axe + b = 0, onde a 0.
neste caso, x 2 ora + b = 0, onde a. neste caso, x 2 or é a o in ine e in in in inde. a e b são números reais chamados de coeficientes da equação.
Teste seus conhecimentos com 10 questões a seguir sobre o tema. Aproveite os comentários após o gabarito para tirar suas dúvidas sobre a resolução.
Questão 1
Resolva as seguintes equações do primeiro grau com uma incógnita.
a) 4x + 2 = 38
b) 9x = 6x + 12
c) 5x – 1 = 3x + 11
d) 2x + 8 = x + 13
Ver Resposta
Respostas 810 a)
x = 9
b) x = 4
c) x = 6
d) x = 5
Para resolver uma equação do primeiro grau devemos isolar a incógnita de um lado da igualdade e os valores Constantes do outro. Lembre-se Que Ao Mudar um termo da equação para o outro lado do sinal de igual devemos инвертор в Operação. Por instanceo, o que estava somando passa a subtair e vice versa.
A) Респоста Correta: x = 9.
B) Респоста Correta: x = 4
C) Resposta Correta: x = 6
D) Restosta orreta: x = 5
d) resposta: x = 5
d) resosta: x = 5
d) resosta: x = 5
d) resosta: x = 5
d) resosta: x = 5
d).
Questão 2
Dentro do conjunto universo Q, разрешение на равенство до 1º степени: 4.(x – 2) – 5.(2 – 3x) = 4.(2x – 6)
Ver Resposta
Respost correta: х = — 6/11.
Primeiramente, devemos eliminar os parênteses. Пункт isso, aplicamos собственность distributiva да multiplicação.
Agora, podemos encontrar o valor da incógnita, isolando o x em um lado da igualdade.
Questão 3
Dada a equação, расчет или доблесть de x.
Ver Resposta
Respost correta: 11/3.
Соблюдайте требования, предъявляемые к equação apresenta frações.
Para resolvê-la precisamos, primeiramente, reduzir as frações ao mesmo denominador. Por isso, devemos calcular или minimo múltiplo comum entre os eles.
Agora, dividimos или MMC 12 pelo denominador de cada fração e o resultado deve ser multiplicado pelo numerador. Esse valor passa a ser o numerador, enquanto que o denominador de todos os termos é 12.
Após cancelar os denominadores, podemos isolar a incógnita e calcular o valor de x.
Questão 4
Define o conjunto solução S da equação do 1º grau .
Ver Resposta
Respost correta: — 1/3.
1º passo: расчетный или MMC dos denominadores.
2-й проход: делитель или MMC pelo denominador de cada fração e multiplicar или resultado pelo numerador. Após isso, substituímos или numerador pelo resultado calculado anteriormente e o denominador pelo MMC.
3º Passo: Cancelar o Denominador, isolar a incógnita e calcular seu valor.
O sinal negativo antes dos parênteses, altera os sinais dos termos que estão dentro.
-1 . 5x = -5x
-1 . (-7) = 7
Continuando a equação:
Questão 5
Resolva as equações 5y + 2 = 8y – 4 e 4x – 2 = 3x + 4 e определить:
numéoric valor a)
b) o valor numérico de x
c) o produto de y por x
d) o quociente de y por x
Ver Resposta
Respostas corretas:
a) y = 2
b) x = 6
c) y.x = 12
d) y/x = 1/3
7
7 ) х = 6
в) у.х = 12
у . х = 2 . 6 = 12
d) y/x = 1/3
Questão 6
Monte as equações que репрезентам as sentenças a seguir e encontre o valor desconhecido.
a) 6 unidades somadas ao dobro de um número é igual a 82. Qual é esse número?
a) 43
b) 38
c) 24
d) 32
Ver Resposta
Resposta correta: b) 38.
Para montar uma doe equação deve: deigo de existir dois membros . Cada componente да equação é chamado де термо.
Os termos do primeiro membro da equação são o dobro do número desconhecido e 6 unidades. Os valores devem ser somados, portanto: 2x + 6.
Já o segundo membro da equação contém o resultado dessa operação, que é 82. Montando a equação do primeiro grau com uma incógnita, temos:
2x + 6 = 82
Agora, resolvemos a equação isolando incógnita em um membro e transferimos o número 6 para o segundo membro. Para fazer isso, o número 6, que era positivo, passa a ser negativo.
2x + 6 = 82
2x = 82 – 6
2x = 76
x = 38
Sendo assim, o número desconhecido é 38. 10 см а mais que o lado menor. Quanto mede или lado menor dessa figura geométrica?
a) 25
b) 30
c) 35
d) 20
Ver Resposta
Resposta correta: d) 20.
O perímetro de um retângulo de seus lados soma.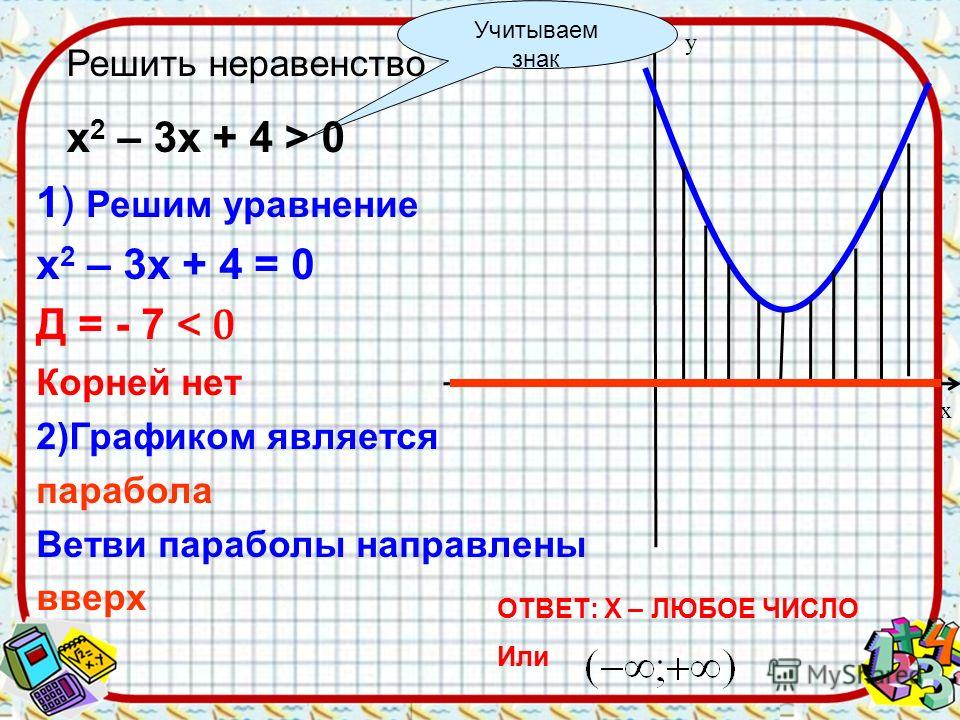
O lado maior é chamado de base e o lado menor é chamado de altura.
De acordo com os dados do enunciado, se o lado menor do retangulo é x, então o lado maior é (x + 10).
Um retangulo é um quadrilátero, portanto seu perímetro é a soma dos dois lados maiores com os dois lados menores. Isso pode ser expresso em forma de equação da seguinte forma:
2x + 2(x+10) = 100
Para encontrar a medida do lado menor, basta resolver a equação.
2x + 2(x+10) = 100
2x + 2x + 20 = 100
4x = 100 – 20
4x = 80
x = 80/4
x = 20 peça de tecido, após a lavagem, perdeu 1/10 de seu comprimento e este ficou medindo 36 metros. Nestas condições, o comprimento, em m, da peça antes da lavagem era igual a:
a) 44
b) 42
c) 40
d) 38
Ver Resposta
Alternativa correta: c) 40.
Podemos utilizar a incógnita x para presentar o comprimento original da peça. Sendo assim, após ser lavada a peça perdeu 1/10 do seu comprimento x.
Первая форма, используемая для решения задачи:
x – 0,1x = 36
0,9x = 36
x = 36/0,9
x = 40 mmc dos denominadores, que é 10.
Agora, calculamos os novos numeradores dividindo или mmc pelo denominador inicial e multiplicamos o resultado pelo numerador inicial. Após isso, cancelamos о denominador 10 de todos os termos e resolvemos a equação.
Portanto, o comprimento original da peça age de 40 m.
Questão 8
(Unicamp-adaptada) Após ter corrido 2/7 de um percurso e, em seguida, caminhando 5/11 do mesmo percurso um atleta verificou que ainda faltavam 600 metros para o final do percurso. Qual o comprimento total do percurso?
a) 2850 м
b) 2120 м
c) 2310 м
d) 2540 м
Ver Resposta
Alternativa correta: c) 2310 м.
Como o percurso total é o valor desconhecido vamos chamá-lo de x.
Os termos do primeiro membro da equação são:
- Corrida: 2/7x
- Каминхада: 5/11x
- Трехо Доп.
: 600
: 600As somas de todos esses valores resultam no comprimento do percurso, que chamamos de x. Portanto, a equação pode ser escrita como:
2/7x + 5/11x + 600 = x
Para Solr essa equação do primeiro grau precisamos calcular o mmc dos denominadores.
mmc (7,11) = 77
Agora, substituímos os termos da equação.
Портанто, общая высота 2310 м.
Questão 9
(Mackenzie) Num exercício de tiro ao alvo, o número de acertos de uma pessoa A foi 40% maior do que B. Se A e B acertaram juntas 720 tiros, então o de B número de a acerto
a) 380.
b) 320.
c) 300.
d) 220.
e) 280.
Ver Resposta
Alternativa correta: c) 300.
Se o número de acertos de B foi x , então a quantidade de acertos de A foi x + 40%. Essa porcentagem pode ser escrita como a fração 40/100 ou como o numero decimal 0,40.
Portanto, a equação que determina a quantidade de acertos pode ser:
x + x + 40/100x = 720 ou x + x + 0,40x = 720
Resolução 1:
Resolução 2:
Portanto, O Número de Acertos de B foi 300.